基于整體觀的單元起始課教學設計與思考

楊慧 吳娜

基于整體觀的單元起始課教學要突出知識的結構性和系統性，幫助學生構建整個單元的“導覽圖”，明晰單元學習框架和研究路徑，強化單元新知與已有認知的內在關聯。正比例函數是學生在初步認識函數概念的基礎上學習的最簡單的初等函數。本節課的教學如何為后續更多復雜函數的學習奠基呢？

一、宏觀把握，突出目標的整體性

《義務教育數學課程標準（2022年版）》指出：函數的教學要通過對現實問題中變量的分析，建立兩個變量之間變化的依賴關系，理解用函數表達變化關系的實際意義；要借助在平面直角坐標系上描點，理解函數圖象與表達式的對應關系，以及函數與對應的方程、不等式的關系，增強幾何直觀；要學會用函數表達現實世界事物的簡單規律，經歷用數學的語言表達現實世界的過程，提升學習數學的興趣，發展應用意識。

本單元的研究內容是一次函數，教材首先編排的是正比例函數內容，這是學生學習特殊函數的第一階段。《正比例函數》作為起始課，教師要從三個維度確定教學目標，引導學生整體感知函數學習的基本框架：一是整體感知初中階段函數模型的研究對象（一次函數→二次函數→反比例函數）；二是整體體驗函數的研究方法（依托實際建模→分析與歸納→辨析與運用）；三是整體構建函數的一般研究路徑（定義→圖象→性質）。

二、循序漸進，突出內容的整體性

本節課的學習要從一般函數的表現形式過渡到具體函數的研究內容，引導學生明確從特殊到一般的函數研究方法，逐步形成函數的一般研究路徑。

1.巧用教材，聚焦函數研究對象

在自主建構函數模型環節，筆者呈現了如下基于教材問題1改編的題目，巧妙引出初中階段函數的研究對象。

京滬高鐵全長1318km，2011年至今已開通運營十多年，累計發送旅客約13億人次。設列車的平均速度為300km/h，請思考以下問題。

（1）京滬高鐵列車行駛過程涉及哪些量？其中哪些是變量？

（2）哪兩個變量之間是函數關系？試說明理由，并寫出函數解析式。

（3）我國正在研發的超級高鐵列車行駛全程所需時間t（單位：h）與行駛速度v（單位：km/h）之間有何數量關系？

以上問題具有進階性，能幫助學生體會函數關系的多樣性及變量與常量的相對性。筆者按照尋找變量→分析關系→建立模型的步驟，逐步引導學生解決問題，認識兩個變量之間的對應規律。在此基礎上，筆者引入其他實例，讓學生感受現實世界中運動變化的普遍性和規律性，如圓的周長[l]隨半徑[r]的變化而變化（[l=]2πr）、正方形的面積S隨邊長[x]的變化而變化（[S=x2]）等。通過分析這些實例中的數量關系，學生列出了形如[y=kx]，[y=kx+b]，[y=ax2+bx+c]，[y=kx]四種類型的函數解析式，為后續函數解析式的分類、概括打下基礎。

2.以生為本，明晰函數概念體系

抽象與概括是數學概念形成的關鍵環節。在分析函數特征環節，筆者先引導學生觀察他們列出的函數解析式（[S=x2]，[y=300t]，[Z=1318-300t]，[l=]2πr，[t=1318v]，[m=7.9V]，[T=-2t]，[Z=1318-y]），分析它們的相同點和不同點。然后，筆者組織學生對函數進行分類，說出分類依據，并給每一類函數命名。有的小組按照等號右邊是整式還是分式，將它們分為整式函數和分式函數；有的小組按照等號右邊是單項式還是多項式，將它們分為單項式函數和多項式函數；還有的小組按照自變量的次數，將它們分為一次函數、二次函數和“負一次”函數。在學生匯報的基礎上，筆者引導學生鞏固了整式、分式、單項式、多項式的概念，形成了正確的分類方法：先按照等號右邊是整式還是分式將其分為整式函數和分式函數，再將整式函數按照自變量的次數分為一次函數和二次函數。學生通過自主探究，不僅明確了特殊函數的分類以解析式特征為標準，還增強了分析、歸納、抽象、概括的能力。最后，筆者從一次函數入手，引導學生比較、分析“[y=300t]，[Z=1318-300t]，[l=]2πr，[m=7.9V]，[T=-2t]，[Z=1318-y]”6個解析式的異同。對于相同點，學生發現這些解析式都可以看成[y=kx+b]的形式，由此歸納出一次函數的概念。對于不同點，學生發現解析式[y=300t]，[m=7.9V]，[l=]2πr，[T=-2t]形式更特殊，它們的常數項[b]等于0，即函數[y]與自變量[x]是正比例關系，由此明確了正比例函數的概念及正比例函數是特殊的一次函數。后續，學生可類比一次函數的定義方式，預測二次函數、反比例函數的形式特征，以構建相對完整的函數概念體系。

三、關注知識銜接，歸納函數的一般研究路徑

1.自主探究，生成函數知識結構

本環節，筆者設計了三個問題，幫助學生明確函數概念的本質，深入理解正比例函數與一次函數的關系。

首先，筆者出示問題1：下列關系式［①[y=-0.1x]，②[y=2x2]，③[y=x3]，④[y=3x]，⑤[y=3（x-1）]，⑥[y2=4x]］中，哪些是一次函數？學生快速判斷出①③是一次函數，⑤去括號后得到的[y=3x-3]也是一次函數。筆者追問：這些一次函數中，哪些是正比例函數？比例系數是多少？學生發現①③是正比例函數，比例系數分別為-0.1和[13]。筆者繼續追問：⑤中[y]是[x-1]的正比例函數嗎？學生將[x-1]當作一個整體，發現[y]與[x-1]是正比例關系，因此，[y]可以看作[x-1]的正比例函數。類似地，學生還判斷出②是二次函數，④是反比例函數等。通過對比和辨析，學生發現了一次函數、二次函數、反比例函數的表象特征，初步構建了函數的知識結構。

然后，筆者出示問題2：下列問題［A.每本書的厚度為0.5cm，一摞書的總厚度[h]與數量[n]的關系。B.圓的面積[S]與半徑[r]的關系。C.某人一年（12個月）的總收入[W]與月平均收入[q]的關系。D.買某種作業本所需的錢數[y]（元）與數量[x]（本）的關系］中，變量之間的關系不是正比例函數的是（? ? ）。這個問題旨在培養學生將實際問題抽象為函數模型的能力。學生自主探究，分別得出各選項中變量之間的函數解析式，確定了答案B。

最后，筆者引導學生完成問題3，即舉出生活中一次函數的例子，進一步體會一次函數應用的廣泛性。結合學生列舉的正比例函數[y=2x]，筆者引導學生深入研究。基于教材上一節內容，學生知道描述函數的方法不僅有解析式法，還有列表法、圖象法。筆者引導學生嘗試列表、畫圖象，并觀察表格和圖象，從數和形兩個角度分析函數的性質，自主歸納函數的特征。這個過程為學生后續深入學習一般一次函數的圖象、性質等奠定了基礎。

2.從整體視角出發，歸納函數研究路徑

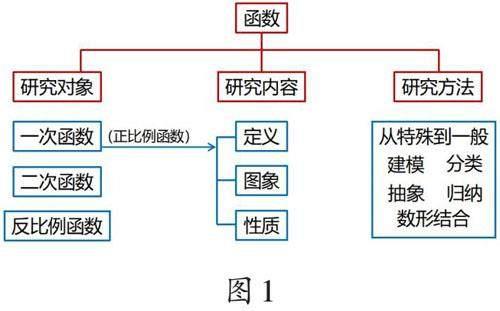
小結環節，筆者引導學生回顧學習過程，總結本節課研究函數的基本路徑，積累研究函數的經驗。學生通過交流、總結，形成如圖1所示的研究框架。

圖1呈現了函數的研究對象、研究內容和研究方法，學生由此形成了單元學習的“導覽圖”。同時，學生歸納出“情境引入變量—明確對應關系—繪制函數圖象—探究函數性質”的具體研究路徑。

（作者單位：襄陽市實驗中學教育集團）