關(guān)于動態(tài)幾何問題解題策略的探究

馬云飛

[ 摘 要 ]瓜豆原理在解析動態(tài)幾何線段、軌跡、路徑問題中十分常用，教學(xué)探究中需要引導(dǎo)學(xué)生總結(jié)方法技巧，探究軌跡模型，并結(jié)合實(shí)例探索構(gòu)建思路.文章通過解讀瓜豆原理，對其常見的兩種類型進(jìn)行應(yīng)用探究.

[ 關(guān)鍵詞 ]瓜豆原理；模型；軌跡；直線；圓弧

動態(tài)幾何問題是初中數(shù)學(xué)重點(diǎn)和難點(diǎn)問題之一，該類問題往往以幾何運(yùn)動為背景進(jìn)行綜合構(gòu)建.對于其中涉及主動點(diǎn)和從動點(diǎn)的情形，可以結(jié)合瓜豆原理模型，利用軌跡思想，明確主、從動點(diǎn)之間的關(guān)系，由軌跡入手逐步破解.下面深入探究瓜豆原理模型，探究解題思路.

方法技巧探究

探究瓜豆原理破解幾何動態(tài)問題，需要關(guān)注以下三大重點(diǎn)：一是原理解讀，二是滿足條件，三是思路構(gòu)建.下面分步探究，具體分析.

1.原理解讀

瓜豆原理適用于主、從動點(diǎn)幾何最值問題，內(nèi)容核心為含有一個(gè)主動點(diǎn)和一個(gè)從動點(diǎn)，受到特定條件的約束，從動點(diǎn)跟隨主動點(diǎn)運(yùn)動，且兩者的軌跡相同.古語：種瓜得瓜，種豆得豆，故而得名.因此該模型原理中有“種”圓得圓，“種”線得線.本質(zhì)上瓜豆原理是關(guān)于幾何旋轉(zhuǎn)、相似的解析構(gòu)造.

2.滿足條件

瓜豆原理適用于幾何動點(diǎn)問題，使用時(shí)需要滿足三大條件：一是問題中含有兩動一定；二是動點(diǎn)與定點(diǎn)之間的連線的夾角為定角；三是動點(diǎn)與定點(diǎn)的距離之比為一定值.

3.思路構(gòu)建

使用瓜豆原理進(jìn)行解題構(gòu)建時(shí)，需分為五步，需要完成動點(diǎn)軌跡確認(rèn)、解題模型構(gòu)建及求解.構(gòu)建思路如下：

第一步，確定主動點(diǎn)的軌跡；

第二步，探尋主動點(diǎn)與從動點(diǎn)之間的關(guān)系；

第三步，確定主動點(diǎn)軌跡的起點(diǎn)、終點(diǎn)；

第四步，結(jié)合相似知識，確定從動點(diǎn)的軌跡；

第五步，根據(jù)動點(diǎn)的軌跡來構(gòu)建模型，求解點(diǎn)、線、圓背景中的路徑長或線段長.

軌跡模型探究

瓜豆原理的軌跡模型常見的有兩種，一種是運(yùn)動軌跡為圓弧，另一種是運(yùn)動軌跡為線段.探究解析時(shí)需要深入解讀模型，掌握其解析思路，總結(jié)相應(yīng)的結(jié)論，為后續(xù)的應(yīng)用探究打下基礎(chǔ)，下面開展模型探究.

模型1：軌跡為圓弧模型

引例：如圖1（a），P為圓O上一個(gè)動點(diǎn)，A為定點(diǎn)，連接AP，Q為AP的中點(diǎn).

思考①：當(dāng)點(diǎn)P在圓O上運(yùn)動時(shí)，點(diǎn)Q的軌跡是什么樣子的？

思考②：分析點(diǎn)Q的軌跡，它與圓O之間有何關(guān)系？

總結(jié)：在上述軌跡為圓模型中，確定點(diǎn)Q的軌跡，實(shí)則就是確定其圓心和半徑，需要從以下三大視角審視模型.

①共線分析：在模型中始終存在三點(diǎn)共線，即點(diǎn)A，Q，P始終共線，由此可得點(diǎn)A，M，O共線.

③縮放分析：從幾何縮放視角分析，可將點(diǎn)Q的軌跡視為點(diǎn)P的軌跡的比例縮放.

基于上述軌跡為圓模型分析，在實(shí)際解析時(shí)需要關(guān)注兩大關(guān)系：一是根據(jù)動點(diǎn)之間的相對位置關(guān)系分析圓心的相對位置關(guān)系；二是根據(jù)動點(diǎn)之間的數(shù)量關(guān)系分析軌跡為圓時(shí)半徑之間的數(shù)量關(guān)系.

模型2：軌跡為線段模型

引例：如圖2（a）所示，△APQ為等腰直角三角形，∠PAQ=90°且AP=AQ.

思考：當(dāng)點(diǎn)P在直線BC上運(yùn)動時(shí)，點(diǎn)Q的軌跡是怎樣的？

分析：當(dāng)AP與AQ的夾角固定，并且兩者的比值為定值時(shí)，點(diǎn)P和Q的軌跡為同一幾何圖形.分析點(diǎn)Q的軌跡，可以任取兩個(gè)時(shí)刻的位置，連接即可.如提取其中的特殊位置，起始點(diǎn)和終止點(diǎn)位置，再連接即可確定點(diǎn)Q的軌跡線段，如圖2（b）所示.

總結(jié)：對于上述軌跡為線段模型，需要滿足對應(yīng)的必要條件，有兩種情形，一是主動點(diǎn)、從動點(diǎn)與定點(diǎn)連線的夾角為定量，即∠PAQ是定值；二是主動點(diǎn)、從動點(diǎn)到定點(diǎn)的距離之比是定量，即AP∶AQ是定值.

模型示例探究

上述探索了瓜豆原理，解讀模型、總結(jié)方法思路，并對其中的兩種模型進(jìn)行深入探究，形成了相應(yīng)的解析策略.下面結(jié)合實(shí)例具體探究，進(jìn)一步總結(jié)方法策略.

1.瓜豆原理之直線軌跡問題

例1 在如圖3所示的平面直角坐標(biāo)系xOy中，已知點(diǎn)A（0，4），P是x軸上的一個(gè)動點(diǎn).現(xiàn)把線段PA繞著點(diǎn)P順時(shí)針旋轉(zhuǎn)60°，得到線段PF，連接OF，則線段OF長的最小值是 .

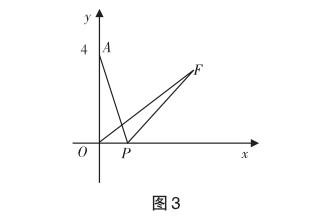
思路分析：本題目為動態(tài)幾何求線段最值問題，以線段PA旋轉(zhuǎn)為背景進(jìn)行綜合構(gòu)建.分析可知其中點(diǎn)A為主動點(diǎn)，點(diǎn)F為從動點(diǎn)，兩點(diǎn)之間由幾何條件進(jìn)行串聯(lián).問題解析時(shí)，可以結(jié)合瓜豆原理，先確認(rèn)動點(diǎn)軌跡，再構(gòu)建最值模型.

過程解析：由條件可知，線段PA繞點(diǎn)P順時(shí)針旋轉(zhuǎn)60°后得到線段PF，根據(jù)旋轉(zhuǎn)特性可知∠APF= 60°，PF=PA，可推知△APF是等邊三角形，則有AP=AF.需要討論點(diǎn)F的位置，分兩種情形：情形1，點(diǎn)F在x軸上；情形2，點(diǎn)F在y軸上.下面分別構(gòu)建模型，討論分析.

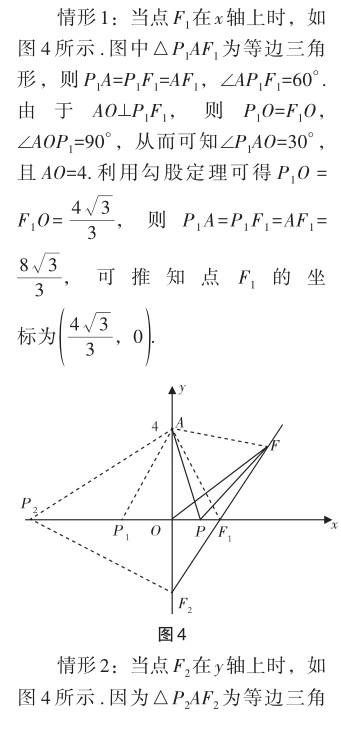
評析：上述求解線段的最小值時(shí)借用了瓜豆原理，分析其中的主動點(diǎn)與從動點(diǎn)的關(guān)系，根據(jù)主動點(diǎn)的軌跡確定從動點(diǎn)的軌跡為直線，屬于瓜豆原理中的直線軌跡類型.探究解析時(shí)需要關(guān)注兩點(diǎn)：一是分析確定主動點(diǎn)軌跡的起始點(diǎn)和終止點(diǎn)；二是把握主動點(diǎn)與從動點(diǎn)的幾何關(guān)系.

2.瓜豆原理之圓弧軌跡問題

例2 如圖5所示，A為坐標(biāo)系第一象限內(nèi)的定點(diǎn)，P是以O(shè)為圓心，2個(gè)單位長度為半徑的圓上的一個(gè)動點(diǎn)，連接AP，以AP為邊向AP右側(cè)作等邊三角形APB.當(dāng)點(diǎn)P在⊙O上運(yùn)動一周時(shí)，點(diǎn)B運(yùn)動的路徑長是 .

思路分析：本題目為與圓相關(guān)的動態(tài)幾何求路徑問題，題目設(shè)定了點(diǎn)P的軌跡，探求點(diǎn)B的運(yùn)動路徑長.需要把握其中的核心條件，即點(diǎn)B是以AP為邊所作的等邊三角形的一個(gè)頂點(diǎn).分析可知問題滿足幾何中的瓜豆原理，點(diǎn)P為主動點(diǎn)，點(diǎn)B為從動點(diǎn)，即可確定點(diǎn)B的軌跡，后續(xù)再根據(jù)移動軌跡求路徑.

過程解析：連接AO，OP，將AO繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)60°，得線段AO′，連接O′B，OO′，如圖6所示.

評析：上述求解動態(tài)幾何中的路徑長，使用了瓜豆原理，分析其中主動點(diǎn)與從動點(diǎn)的關(guān)系，確定動點(diǎn)的軌跡，進(jìn)而完成路徑求解.對于瓜豆原理中的圓弧軌跡問題，需要注意兩點(diǎn)：一是分析其中的幾何特性，構(gòu)建主動點(diǎn)與從動點(diǎn)之間的聯(lián)系；二是關(guān)注動點(diǎn)的運(yùn)動軌跡，包括圓弧的圓心和半徑長.

解題教學(xué)建議

上述對動態(tài)幾何中的瓜豆原理進(jìn)行深入探究，總結(jié)了方法技巧，解讀了模型特性，并結(jié)合實(shí)例對兩種軌跡類型進(jìn)行探究，下面提出幾點(diǎn)建議.

1.深入知識本質(zhì)，總結(jié)方法技巧

瓜豆原理模型是破解動態(tài)幾何問題常用的方法策略，探究解析時(shí)需要注意深入知識本質(zhì)，同時(shí)全面解析突破的方法技巧.教學(xué)探究時(shí)，可從以下三個(gè)方面進(jìn)行：一是具體解讀模型的原理，挖掘知識本質(zhì)；二是對其適用條件進(jìn)行剖析，分析條件之間的關(guān)聯(lián)；三是構(gòu)建解題應(yīng)用的思路，形成分步策略.

2.總結(jié)模型類型，實(shí)例探索構(gòu)建

動態(tài)幾何問題在初中數(shù)學(xué)中十分常見，利用瓜豆原理模型探究突破時(shí)要注意類型解讀，并結(jié)合實(shí)例分類構(gòu)建.教學(xué)中教師需對常用模型進(jìn)行深入分類解析，即軌跡為直線型和軌跡為圓弧型，并精選問題引導(dǎo)學(xué)生體驗(yàn)構(gòu)建過程.教學(xué)時(shí)需要注意以下三點(diǎn)：一是對類型進(jìn)行引例分析，總結(jié)解析思路；二是實(shí)例探究注意思路引導(dǎo)，引導(dǎo)學(xué)生逐步思考；三是注意解后評析，讓學(xué)生思考解題過程，總結(jié)方法思路，積累解題經(jīng)驗(yàn).

3.滲透思想方法，提升綜合素養(yǎng)

在動態(tài)幾何問題的探究解析中，教師需要注意合理滲透數(shù)學(xué)思想方法，通過思想方法教學(xué)來提升學(xué)生的綜合素養(yǎng).教學(xué)時(shí)可從以下兩個(gè)方面進(jìn)行：一是滲透模型思想，構(gòu)建瓜豆原理的解析模型，引導(dǎo)學(xué)生關(guān)注模型構(gòu)建的過程；二是滲透數(shù)形結(jié)合思想.動態(tài)幾何問題解析時(shí)需要利用數(shù)形結(jié)合的方法技巧，教學(xué)時(shí)要引導(dǎo)學(xué)生掌握具體的方法，由“數(shù)”照“形”，以“形”釋“數(shù)”.