關于中點四邊形模型的探究思考

孫鍇

[ 摘 要 ]中點四邊形模型是初中數學探究的重點，涉及三角形中位線定理、特殊圖形的判定定理等知識.解讀模型、總結結論、應用強化對于提升學生的知識水平和解題能力有極大的幫助.文章探究中點四邊形模型，開展模型教學思考，提出相應的教學建議.

[ 關鍵詞 ]平行四邊形；中點；模型；菱形；矩形

中點四邊形模型是一種特殊的幾何模型，該模型以四邊形的中點為基礎構建，形成的新圖形為平行四邊形，且增加幾何條件可形成特殊的平行四邊形.本文將深入探究中點四邊形模型，并結合實例突破解題探究.

引例探究

引例：如圖1所示，四邊形ABCD四邊的中點分別為E，F，G，H，順次連接E，F，G，H四點，試判斷四邊形EFGH的形狀，并說明理由.

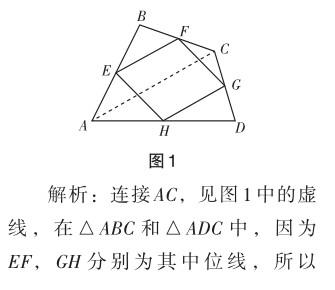
點評：上述探究四邊形EFGH的形狀，即任意四邊形中點連線所得圖形的形狀，根據上述結論可知為平行四邊形.實際上上述題目涉及中點四邊形模型，即依次連接四邊形四邊的中點，所得四邊形即為中點四邊形，其知識核心為三角形的中位線的性質定理.

模型總結

中點四邊形模型在初中數學中十分常見，增設條件不同，所獲得的平行四邊形不同，可將平行四邊形演變為菱形、矩形、正方形，下面深入探究，總結模型.

中點模型1——矩形

增設條件：對角線垂直（圖2中BD⊥AC）.

結論：對角線垂直的四邊形的中點四邊形是矩形.

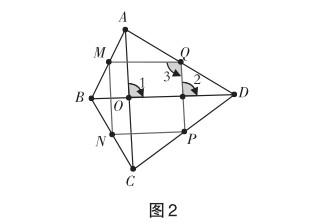
證明：點M，N，P，Q分別是任意四邊形ABCD四邊的中點，由引例結論可知四邊形MNPQ為平行四邊形.

由于AC∥PQ，則∠2=∠1=90°.又知MQ∥BD，所以∠3=∠2=90°.可證四邊形MNPQ為矩形.

中點模型2——菱形

增設條件：對角線相等（圖3中BD=AC）.

結論：對角線相等的四邊形的中點四邊形是菱形.

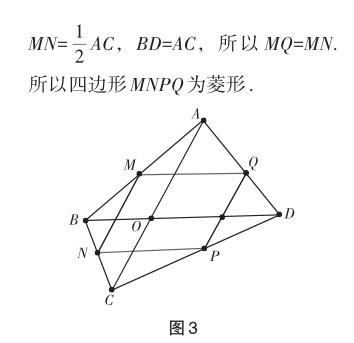
中點模型3——正方形

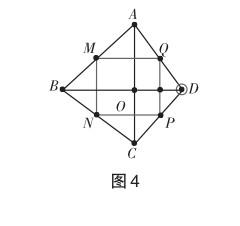
增設條件：對角線平行且相等（圖4中BD⊥AC，且BD=AC）.

結論：對角線垂直且相等的四邊形的中點四邊形是正方形.

證明：根據模型2的思路可先證明四邊形MNPQ為菱形，再結合模型1的結論可證明其為矩形，進而可證明其為正方形.

解題探究

上述具體探究了三種特殊的中點四邊形模型，即菱形、矩形、正方形成立的條件，并總結結論，探索證明過程.而在實際考查時，中考模型問題的題型多樣、綜合性強，下面結合實例具體探究、解析.

1.模型中的綜合探究

例1 在四邊形ABCD中，點E，F，G，H分別為邊AB，BC，CD，DA的中點，順次連接各邊中點得到的新四邊形EFGH稱為中點四邊形（如圖5所示）.

（1）我們知道：無論四邊形ABCD怎樣變化，它的中點四邊形EFGH都是平行四邊形.特殊的：

①當對角線AC = BD時，四邊形ABCD的中點四邊形為 形；

②當對角線AC⊥BD時，四邊形ABCD的中點四邊形是 形.

（2）如圖5，在四邊形ABCD中，已知∠B =∠C = 60°，且BC = AB + CD，請利用（1）中的結論，判斷四邊形ABCD的中點四邊形EFGH的形狀并進行證明.

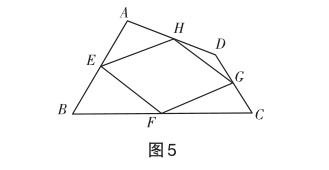
思路分析：上述為幾何中較為特殊的中點四邊形模型問題，題設兩問，分別探討特殊條件下四邊形的形狀.解析探究時要結合中點四邊形模型的相關知識，結合題設條件按照“四邊形→平行四邊形→特殊圖形”的思路來證明.

過程解析：（1）①該問探究“對角線相等”條件下的中點四邊形形狀，可連接AC，BD，利用三角形中位線定理來證明四邊形EFGH是平行四邊形，再證明其為特殊圖形.

連接AC，BD，如圖6所示.已知點E，F，G，H分別為AB，BC，CD，DA的中點，則EH∥BD，FG∥BD，所以EH∥FG.同理可證EF∥HG，所以四邊形EFGH是平行四邊形.

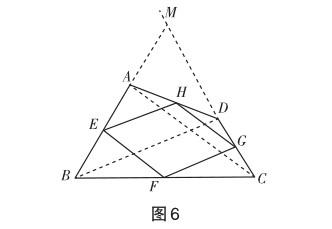
已知對角線AC=BD，所以EH= EF，可證四邊形ABCD的中點四邊形是菱形.

②該問探究“對角線垂直”條件下的四邊形形狀，把握其中的垂直關系即可.

當對角線AC⊥BD時，EF⊥EH，所以四邊形ABCD的中點四邊形是矩形.

（2）該問探究等角關系及線段關系下的中點四邊形形狀，可證明其中的全等三角形，再利用其結合第（1）問的條件來得出結論.

解后評析：上述以中點四邊形模型為背景開展幾何探究，題設兩問，設定不同條件來探究四邊形的形狀.解析探究時，要充分利用圖形的性質條件，作輔助線構建模型.上述解析過程涉及矩形、菱形的判定和中點四邊形的定義，掌握中點四邊形的概念、矩形及菱形的判定定理是解題的關鍵.

2.新定義中的模型探究

例2 我們給出如下定義：順次連接任意一個四邊形各邊的中點所得的四邊形叫中點四邊形.

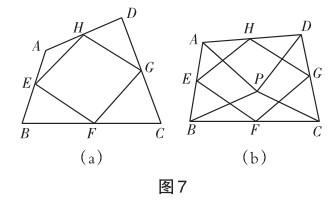
（1）如圖7（a），在四邊形ABCD中，點E，F，G，H分別為邊AB，BC，CD，DA的中點，中點四邊形EFGH是 .

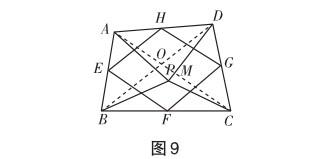
（2）如圖7（b），P是四邊形ABCD內一點，且滿足PA=PB，PC= PD，∠APB=∠CPD，點E，F，G，H分別為邊AB，BC，CD，DA的中點.猜想中點四邊形EFGH的形狀，并證明你的猜想.

（3）若改變（2）中的條件，使∠APB=∠CPD=90°，其他條件不變，直接寫出中點四邊形EFGH的形狀（不必證明）.

思路分析：上述以新定義的命題形式考查中點四邊形模型，解析探究時要理解新定義，即中點四邊形的定義，挖掘其中的性質定理.后續探究時要充分利用設定條件，按照“四邊形→平行四邊形→特殊圖形”的思路來逐步探究.

過程解析：（1）該問證明中點四邊形的性質，實則考查對新定義的理解，利用三角形的中位線定理即可推出結論.

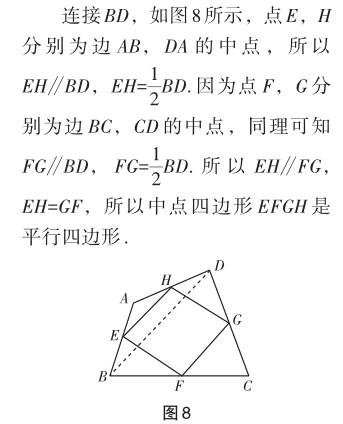
（2）該問進一步設定條件，涉及等邊、等角條件，猜想驗證中點四邊形EFGH的形狀.探究時可提取其中的特殊三角形，利用其性質來推導結論.

結合第（1）問可知中點四邊形EFGH是平行四邊形，所以平行四邊形EFGH是菱形.

（3）該問進一步變更條件探究中點四邊形的性質，分析猜想可知其為正方形，則可按照“特殊四邊形→菱形→正方形”的思路逐步證明.

解后評析：上述以新定義的形式考查中點四邊形模型，問題整體上具有關聯探究的特點，所涉三小問之間具有相關性，其結論可以互通互用.解析突破時要理解定義、合理猜想、嚴謹論證，利用特殊四邊形的證明思路，作圖建模，推導論證.

教學思考

上述圍繞中點四邊形模型開展探究，總結模型結論，探索證明思路，并結合實例進行拓展探究，整個過程對于強化學生基礎知識，培養探究能力極為有利.同時模型的探究思路具有一定的教學參考價值，下面結合教學實踐進一步思考，提出幾點建議.

1.以基礎知識為探究出發點

幾何模型探究是初中數學教學的重要內容，有利于幾何知識整合與重構，可幫助學生梳理知識網，強化知識基礎.模型探究時要以基礎知識作為出發點，立足教材的性質定理，引導學生思考，逐步構建模型.以上述中點四邊形模型為例，探究時立足三角形中位線定理、平行四邊形判定定理，構建幾何模型.具體教學中要注意兩點：一是引導學生理解定理，掌握定理本質；二是讓學生體會模型的構建過程，感悟模型結構.

2.將模型總結作為探究關鍵

幾何模型探究中要注意總結歸納，即總結模型特征、證明思路、幾何結論，探究時按照“特征分析、定理證明、結論總結”的思路來開展.以上述中點四邊形模型為例，從引例入手呈現構建過程；分步探究總結模型的三種情形，并加以證明.因此，教學中教師要注意引導學生總結模型，掌握模型問題的探究思路.可分如下三個環節來開展：一是構建探索，引導學生探索模型特征；二是開展模型“猜想—驗證”，培養學生的思維能力；三是總結模型結論，指導學生總結歸納，生成幾何結論.

3.將應用強化作為教學重點

“應用強化”是模型探究的重要環節，應作為教學的重點，即針對幾何模型精選問題，引導學生開展解題探究，應用模型知識及分析思路來處理問題，提升學生的知識應用能力.以上述中點四邊形模型的解題探究為例，從“知識綜合”和“新定義拓展”兩大視角設定問題，按照“思路分析—過程解析—解后評析”的思路進行解題探究.探究過程中注意學生的思維培養，滲透數學的思想方法，提升學生的綜合能力.

寫在最后

開展模型教學時教師要注意采用合適的方法，注意引導學生立足教材中的定理，探索構建過程，總結模型結論，積累探究經驗.通過模型探究，幫助學生強化基礎知識，構建知識網絡，提升思維能力，培養核心素養.