基于教學評一體化的初中生幾何推理能力培養行動研究
陳琴琴
[ 摘 要 ]“教學評一體化”作為一種教學思想與手段,將其應用于課堂教學中,有利于提升教學效果和學習效率.在培養學生幾何推理能力的過程中,教師作為課堂教學的引導者,必須更新教學觀念,突破傳統教學的束縛,重視“教學評一體化”的應用,結合教學中的反饋進行適時、適度的啟發和指導,以此逐步提升學生的幾何推理能力,發展學生的數學核心素養.
[ 關鍵詞 ]垂線段;最短;定義;模型;最值
基金項目:福建省福州市教育科學研究“十四五”規劃2023年度課題“基于教學評一體化的初中生幾何推理能力培養行動研究”(FZ2023GH051).
《義務教育數學課程標準(2022年版)》指出,完整的教學活動包括教、學、評三個方面.在課堂教學中,要把教、學與評價相互整合,既要考慮教什么、怎么教,為什么教,明確教學中學生應具有的學習效果,還要關注學生的學習過程,了解學生學會了什么,有沒有達到預期要求,并根據實際反饋及時調整教學計劃和教學策略,真正做到“教學評一體化”.不過在實際教學中,部分教師為了趕進度,只管教什么和怎么教,卻不關注教學結果,只是為了教而教.教、學、評的相互分離,很容易使課程的實施偏移預設的軌道,影響教學質量和學習效果.因此在實際教學中,教師要明確教學目標與學習結果,進而為教與學提供方向,為評提供依據.
若想學好初中數學,學生需要具備一定的幾何推理能力,但是從目前整體水平來看,很多學生幾何推理能力存在不足,表現為推理意識不強,并未形成良好的推理習慣,思維缺乏嚴謹性、變通性.為了改變這一局面,教學中教師不僅要關注自身的教,更要關注學生的學,要提供時間和空間讓學生思考與探究,并結合課堂生成進行適時的評價和引導,真正做到教學評一體化,推動學生幾何推理能力的提升.下面,筆者結合教學經驗分析培養學生幾何推理過程中存在的問題,并提出幾點建議.
培養學生幾何推理能力過程中存在的問題
1.缺乏一定的幾何推理意識
在初中數學教學中,部分教師側重于教,常常大包大攬,忽視了學生的學.“以教代學”的教學模式影響學生自主學習能力的提升,影響學生幾何推理能力的培養.從整體來看,初中生普遍存在推理意識不強的問題,表現為思路混亂.
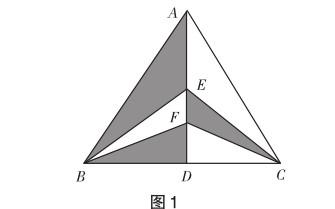
例如,如圖1,在△ABC中,AC=AB=5,BC=6,AD是BC邊上的中線,點E,F分別是AD上兩點,求陰影部分的面積.問題給出后,大多數學生首先想到的就是分別計算出陰影部分的面積,再將各陰影部分的面積相加,但是根據已知,無法計算出AE,EF,FD的長度,所以沒有得到答案.之所以出現以上情況,是因為學生還沒有形成推理習慣,解題時習慣于生搬硬套.根據已知條件可知△ABC是等腰三角形,又AD是△ABC的中線,根據等腰三角形“三線合一”定理可知,AD也是等腰三角形的高,所以△ABD和△ADC的面積相等.又BD = DC,且AD⊥BC,所以S△BEF=S△CEF,這樣問題便轉化為求△ABC面積的一半.對于該題,如果學生有較好的幾何推理意識和轉化意識,問題便可迎刃而解.
2.缺乏數學思維的嚴謹性
數學是一門非常嚴謹的學科,常常是“一字之差,謬以千里”.在幾何問題的解決過程中,答案的準確與否取決于每個推理環節結論準確與否,只有確保每步推理都是合理的、正確的,才能得到正確的答案.顯然其對學生的思維嚴謹性有著較高的要求.

3.缺乏足夠的合情推理能力
在教學中,課堂教學側重于培養學生的演繹推理能力,而忽視對學生合情推理能力的培養,使得學生對合情推理方面的知識與技能掌握較少.合情推理的結論雖然不夠嚴謹,但它在很多時候是演繹推理的“引路人”.
例如,以圖1中計算陰影部分的面積為例,若學生通過觀察能夠猜想出所求陰影面積為△ABC面積的一半,那么學生在解題時就可以此為條件,反向尋找線索.不過從學生的解題反饋來看,大多數學生的合情推理能力不高,他們局限于根據已知條件來推導答案.
培養學生幾何推理能力的策略研究
1.培養推理意識,提升學生幾何推理能力
推理意識應是初中生應具備的素養之一.在幾何教學中,為了更好地培養學生的推理意識,教師首先要讓學生發現幾何證明的樂趣,讓學生獲得成功的體驗,以此激發學生學習幾何的興趣;其次要重視概念、公式、定理等基礎知識的推導,培養學生靈活應用基礎知識解決問題的能力;最后要引導學生梳理解題過程,并鼓勵學生創新推理方法.逐層的引導與訓練,能為學生幾何推理能力的提升打下堅實的基礎.
2.精心設計問題,培養學生合情推理能力
學生合情推理能力的培養是一個緩慢的過程,需要教師在日常教學中慢慢啟發、引導.教師要改變傳統的講練模式,給學生提供一定的觀察、思考、探索、歸納的時間和空間,培養和鍛煉學生的合情推理能力.在具體實施過程中,教師可以精心設計問題鏈,并提供機會讓學生獨立思考和合作探究,同時對各種課堂生成給予及時的、正面的評價,以有效規避講練模式的枯燥感,通過教學評一體化的應用,潛移默化地提升學生的合情推理能力.
例如,學習了四邊形相關知識后,教師從學生現有認知水平出發,設計了如下問題鏈:
(1)已知E,F,G,H是平行四邊形ABCD各邊中點,試猜想四邊形EFGH是什么四邊形,并加以證明;
(2)已知E,F,G,H是矩形ABCD各邊中點,試猜想四邊形EFGH是什么四邊形,并加以證明;
(3)已知E,F,G,H是菱形ABCD各邊中點,試猜想四邊形EFGH是什么四邊形,并加以證明;
(4)已知E,F,G,H是正方形ABCD各邊中點,試猜想四邊形EFGH是什么四邊形,并加以證明;
(5)已知E,F,G,H是任意四邊形ABCD各邊中點,試猜想四邊形EFGH是什么四邊形,并加以證明.
教學中,教師可以引導學生畫一畫、量一量,結合實驗結果提出自己的猜想,并鼓勵學生根據幾何基礎知識進行推理、驗證.在此過程中,教師要鼓勵學生爭論,并提供機會進行生生互評,以此通過經歷操作、猜想、推理、驗證、爭論、評價等過程,加深對相關知識的理解,提升學生的幾何推理能力.
3.重視解題規范,培養數學思維的嚴謹性
幾何證明是幾何教學的重中之重,也是培養學生幾何推理能力的必經之路.對于初學幾何證明的初一新生來講,幾何證明是一個難點.學生對幾何證明的學習主要源于教師的講授,學生學習幾何證明大多從模仿開始.教學中,教師要充分發揮例、習題的示范功能,幫助學生養成規范解答的好習慣,以此培養學生數學思維的嚴謹性,提升學生的幾何推理能力.教師不要急于呈現證明過程,應先帶領學生思考這樣幾個問題:(1)證明該題需要分幾步?(2)先證什么?(3)再證什么?這樣通過逐層分析得到解題路徑后,教師要鼓勵學生將問題進行到底,并讓學生對解題過程進行點評,以幫助學生形成解題規范,提高學生的幾何推理能力.
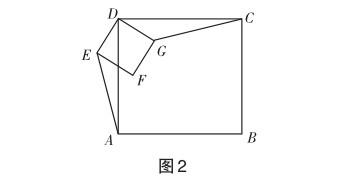
例如,如圖2,已知四邊形ABCD和四邊形DEFG都是正方形,求證:AE=CG.


在幾何教學中,尤其在學生初學幾何證明時,教師一定要重視學生的書寫規范,確保證明過程嚴謹、順暢,每步都有理有據,有效避免出現一些“想當然”的錯誤,以此培養學生數學思維的嚴謹性,提高學生的邏輯推理素養.
總之,培養學生幾何推理能力不是一蹴而就的,教學中教師要分析影響學生幾何推理能力提升的原因,并結合教學實際適度引導,以此通過“教學評一體化”教學原則的落實,提升課堂教學效果,發展學生的幾何推理能力.

