融合數學建模思想的物流管理課程教學研究

紀海峰 楊真真

摘 要：隨著經濟的全球化，物流業的發展急速加快，促進培養了更多的物流管理專業人才。數學建模作為聯系實際問題和數學的橋梁，在人才培養上有著重要的作用。在物流管理專業課程的教學中融入數學建模的思想和過程，不僅可以豐富課堂教學內容，而且能夠培養學生解決實際問題的能力，提高學生的綜合素質。文章首先詳細介紹了數學建模的基本概念和流程，分析了其在物流管理中的重要性，然后以物流中心選址為例，研究了數學建模在物流管理課程教學中的應用。

關鍵詞：數學建模；物流管理；高等教育

中圖分類號：F259.22；G642文獻標志碼：ADOI：10.13714/j.cnki.1002-3100.2024.10.034

Abstract： With the globalization of the economy， the development of the logistics industry is accelerating rapidly，? which promotes the training of more students majoring in logistics management. Mathematical modeling， a bridge connecting the practical problems and the mathematics， plays an important role in talent cultivation. Integrating the thought and process of mathematical modeling into the teaching of logistics management courses can not only enrich the teaching content， but also cultivate students' ability to solve practical problems and improve their comprehensive quality. This paper first presents the basic concept and process of mathematical modeling， analyzes its importance in logistics management， and then studies the application of mathematical modeling in the course of logistics management by taking the issue of finding the location of logistics center as an example.

Key words： mathematical modeling; logistics management; higher education

0? ? 引? ? 言

中國是全球經濟增長的重要貢獻者之一，物流是經濟發展的重要一環，起著促進貿易、降低成本、推動經濟發展的作用，以物流形成的產業也是國民經濟的重要部分。隨著經濟全球化的深入和網絡經濟的興起，物流業的發展也急速加快[1-2]。實現快速的發展需要人才的支持，特別是具有物流管理方面知識的高素質人才的支持。目前，如何培養出能夠勝任新形勢下所需的物流管理方面的高級人才一直是高校探索的方向。隨著大數據、人工智能等新技術的出現，物流業也逐漸向智能化轉化[3]，而大數據、人工智能又涉及到多學科融合，這給物流專業的人才培養提出了新的要求。高校需從教學與實踐環節進行深入思考，追蹤物流業的發展趨勢，為我國培養優秀的物流人才[4]。

數學是人類智慧的結晶，也是一個有力的工具。正如馬克思所說“一門科學只有在成功地運用了數學時，才算是達到了真正完善的地步。”數學建模利用數學知識解決實際問題，是聯系數學知識和實際問題的橋梁[5]。數學建模通過對實際問題的本質規律進行提煉，建立數學化的模型，并利用數學知識和計算機手段對模型進行求解，達到解決實際問題或指導實際生產的目的。無論是大數據、人工智能的新技術還是物流專業傳統的專業課，數學建模思想都在其中發揮著重要作用。

南京郵電大學的物流管理專業開設在現代郵政學院之下，其培養目標為：“本專業培養適應現代物流服務業發展需要，以管理學科為理論基礎，經濟、管理、工學學科相互滲透，具有較高的思想道德和文化修養，具有國際視野、創新精神和實踐能力的物流管理專業人才。”南京郵電大學物流管理專業的學生，在大一學習高等數學課程之后，已經掌握了必要的數學知識，具備一定的利用數學知識解決實際問題的能力，這為后續物流管理專業的專業課提供了數學基礎。物流管理中涉及到許多模型，例如物流需求預測模型、庫存控制模型、物流運輸決策模型、物流網點選址模型等[6]，這些模型實際上都屬于數學建模的范疇。如果任課教師能充分了解數學建模的一些基本概念、思想以及流程，并貫穿到課堂教學中，那么學生將更容易理解這些模型的來龍去脈，并且在遇到新的問題時，可以利用數學建模的思想，建立自己的數學模型，達到舉一反三的效果。

1? ? 數學建模概述

1.1? ? 數學建模基本概念

在現實生活中隨處可見各種各樣的模型，例如：汽車玩具模型、展覽廳的城市規劃模型等。而數學模型是一種抽象的模型，是為了達到某個目標，在某些假設下提煉出來的數學結構，例如微分方程和線性規劃等。數學建模是指建立并求解數學模型的全過程，它主要包含5個部分：問題的提出、模型的建立、模型的求解、模型的檢驗以及模型的應用。

1.2? ? 數學建模基本步驟

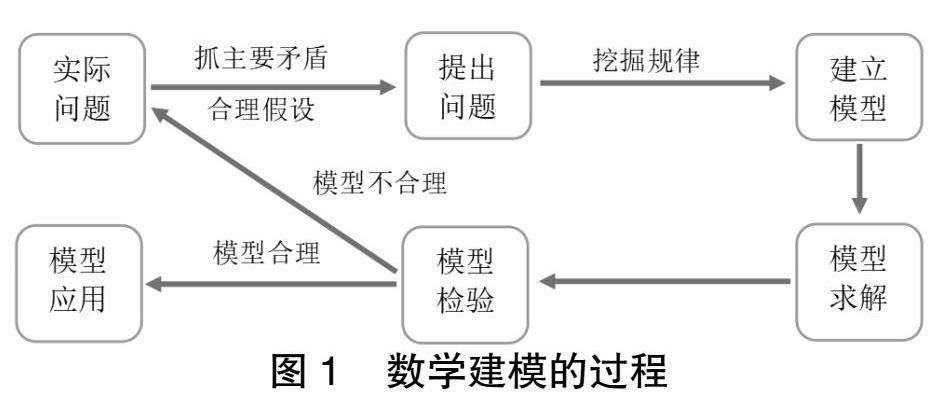
數學建模的過程大致如圖1所示。

第一步：針對研究的實際問題，如物流網點選址問題，提出數學問題。這里需要了解問題的背景，明確研究的目的，收集相關數據，抓住問題的主要矛盾，做出合理的假設，用數學語言將實際問題簡化，抽象成一個數學問題。

第二步：基于第一步的假設，充分挖掘問題的內在規律，利用數學知識，選擇合適的建模方法，建立與問題相適應的數學模型。這一步用到的數學知識較多，考察學生對數學基礎知識的掌握情況。

第三步：利用數學上的解析方法或數值方法，自己編程或借助已有的軟件，精確或近似地求解所建立的數學模型。這一步考察學生的團隊協作能力以及動手實踐能力。

第四步：對模型的靈敏度和穩健性進行分析，判斷模型的優劣。對模型的計算結果進行分析，檢驗是否和實際一致。如果不一致，說明模型不合理，需要返回第一步，判斷假設是否合理，對模型進行修正。

第五步：如果第四步對模型的檢驗沒有發現與實際問題不一致的情況，說明模型基本是合理的，可以把模型應用到實際問題中。這一步需要注意的是，需要對所得結果用非數學的語言重新表述，使得非數學專業的問題提出者能夠理解。

1.3? ? 能力的培養

數學建模不僅能解決實際問題，在物流管理中還有著重要的應用，而且也是培養學生能力的一個有效手段。通過數學建模，學生能提高查閱資料的能力、化繁為簡抽象思維的能力、分析解決問題的能力以及動手實踐的能力等。

2? ? 融合數學建模的課堂教學示例

在物流定量模型與應用這門課上，有一個關于物流網點選址的知識點[7]。這一節以該知識點為例，按照上一節給出的方法和步驟，給出融合數學建模思想的教學實例。

2.1? ? 實際問題的描述

首先，對學生描述實際遇到的物流選址問題及其重要性。物流網點或倉庫的選址是一個十分重要的決策問題，是物流網格規劃的重要內容。合理的選址有利于充分利用資源，降低成本，促進經濟發展，提高經濟效益。如果選址不當，會造成資源浪費，給企業帶來無法彌補的缺陷。假設某工廠生產某種產品，先運送到物流中心，再從物流中心分發到零售商，那么如何科學合理地選址物流中心的地址呢？

2.2? ? 數學問題的提出

接著，給學生展示如何提出數學問題。為了抓住主要矛盾，需要對問題做一些簡化假設。假設工廠的位置是確定的，它的生產能力能夠充分滿足需求。此外，假設每個零售商的位置和銷量也是確定的。為了簡化，只考慮一個物流中心的選址，且不考慮工廠到物流中心的運輸成本和倉庫的管理費用，只考慮物流中心到零售商的運送費用。基于上述假設，物流中心的選址問題就變成要求物流中心的位置坐標使得總物流費用H最小的問題。

2.3? ? 數學模型的建立

給學生示范怎樣推導數學模型。為了建立數學模型，需要用符號定義一些量。設零售商的個數為，每個零售商的位置坐標為，，所需求解的物流中心的位置坐標為，該物流中心到第個零售商的運送費用為，則總的物流費用可以表示成，其中又可以表示為，這里表示從物流中心到第個零售商的運送費率，即單位噸單位公里的運送費用；表示第個零售商的貨物需求量；表示物流中心到第個零售商的距離，即：。

假設在區域上進行選址，且物流中心的地址有一些限制條件那么選址問題的數學模型為如下帶約束的最優化問題。

2.4? ? 數學模型的求解

在模型建立后，需要對模型的目標函數和約束條件進行分析。如果約束條件較弱，則可以近似成無約束的優化問題。這時借助數學理論，其最優解實際上是目標函數偏導數為零的解，即：

。

這里考察學生高等數學知識的學習情況，不會的學生需要復習高等數學中偏導數計算的知識點。由于上式右端中還含有未知量，因此需要采用不動點迭代法求解。在應用迭代法求解時可以將零售商的幾何重心作為初始值，加快算法收斂。

如果模型帶有復雜的約束條件，上述方法則不再適用，可以借助計算機軟件進行求解[8]，例如Lingo軟件、Matlab軟件以及國產北太天元軟件等。在實踐教學中，可以將學生進行分組，每一個組分配不同的算法及軟件，比較不同算法和軟件之間的優缺點，提高學生的積極性和動手能力。在每個組內，鼓勵學生協同合作，例如將編寫程序、數據處理、結果分析等任務分給不同的學生，提高團隊協作能力。

2.5? ? 模型的檢驗及修正

上述模型是基于一些簡化而得到的。如果問題比較復雜，需要考慮工廠到物流中心的運輸費用F以及物流中心的建設費用，那么上述模型的目標函數需要改成。

上式中，和是物流中心的地址的函數，即，。由于不同地方的土地成本不同，因此物流中心的建設用與地址相關是合理的。修正后的模型比較復雜，需要借助計算機軟件求解。

在課堂上講解這一知識點時，可以讓學生開動腦筋，思考這個模型是否還可以進一步改進。實際上，兩點之間的運輸是通過曲折的道路相連接的，不是簡單的直線，這時可以在距離計算公式中添加一個系數加以修正，以得到更加準確的數學模型。

2.6? ? 實際問題的應用

給學生展示如何把上述模型應用到實際問題中。零售商的地址坐標和貨物需求量如表1所示。

不考慮工廠到物流中心的運輸費用以及物流中心的建設費用，利用建立的數學模型求解。將學生分成兩組，一組通過迭代法求解，另一組利用Lingo軟件進行求解。在迭代法中，先通過數學公式計算出4個零售商的重心為（7.8，4.9），再把其作為初始值帶入到迭代法中，得到如下結果，如表2所示。

另一組學生通過Lingo軟件中的優化函數求解，也選擇重心（7.8，4.9）作為初始值，得到與表2中相同的結果。

3? ? 結束語

通過對選址問題知識點的教學，可以看出數學建模過程的引入對物流管理課程的教學是有效的，學生更容易理清從實際問題到數學問題的過程。當然，針對不同的知識點，教師也必須根據具體問題設計具體的教學方案。在物流管理專業課程中融入數學建模的思想和過程，不僅豐富了課堂教學，還培養了學生解決問題的能力，提高了學生的素質，在物流人才的培養方面起到了積極的作用。

參考文獻：

[1] 楊明．國際物流信息化發展趨勢及策略[J]．中國物流與采購，2023（3）：108-109．

[2] 何黎明．中國物流技術發展報告2020[M]．北京：中國財富出版社有限公司，2021．

[3] 謝美娥．大數據在物流管理中的應用研究[J]．物流工程與管理，2020，42（3）：49-51．

[4] 魏杰羽．高職物流專業人才通識素養與教育現狀分析[J]．物流工程與管理，2015，37（8）：139-140．

[5] 李大潛．數學建模是開啟數學大門的金鑰匙[J]．數學建模及其應用，2020，9（1）：1-8．

[6] 汪曉銀，吳雄華．從科學研究的視角重構數學建模教學[J]．數學建模及其應用，2018，7（4）：25-29．

[7] 趙剛，沈家驊，王立坤．物流定量模型與應用[M]．成都：四川人民出版社，2009．

[8] 曾琢．線性規劃法在物流管理中的應用[J]．中國市場，2015（7）：24-25．