黃土高原SRC參數的空間物理釋義與流量估算應用

薛超偉　張洪波　冶兆霞　張雨柔　楊志芳　趙孝威　李同方

摘 要：黃土高原地處我國西北旱區，降水稀少且潛在蒸發強烈，包氣帶較厚且空間異質性大等多種問題交織耦合導致區域河川徑流演化機制極其復雜，影響區域生態保護與高質量發展的進程。對黃土高原不同生態分區的１０ 個代表性流域的ＳＲＣ 參數進行空間分析，研究了ＳＲＣ 參數的異質性分布規律，探析了ＳＲＣ 參數在黃土高原地區的物理釋義，并基于ＳＲＣ 建立了流域出口斷面流量與陸地水儲量的區域化響應關系，實現了通過ＧＲＡＣＥ 重力衛星反演數據對流域出口斷面流量的初步估算。研究表明，同一生態區內ＳＲＣ 參數α、β 具有一定的穩定性，其中β 和流域的干旱指數成負相關關系，與平均坡度成正相關關系，在地理位置中隨緯度的減小和經度的增大而增大；而α 則和土壤孔隙度存在正相關關系，與導水率衰減參數存在負相關關系。通過冪函數可建立黃土高原流域陸地水儲量與出口斷面流量間的擬合關系，并形成適用于平穩ＧＲＡＣＥ 數據的流域流量過程估算方法。

關鍵詞：ＳＲＣ；特征參數；空間分布；影響因素；ＧＲＡＣＥ；黃土高原

中圖分類號：ＴＶ６２；ＴＶ８８２．１ 文獻標志碼：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２４．０４．００４

引用格式：薛超偉，張洪波，冶兆霞，等．黃土高原ＳＲＣ 參數的空間物理釋義與流量估算應用［Ｊ］．人民黃河，２０２４，４６（４）：２３－３１．

０ 引言

水文循環過程是地球陸地系統的重要組成部分，其驅動地表通量變化進而影響流域陸面演化進程及空間分布格局。土壤類型、坡度、干旱指數等作為流域地表特征變量，也會通過陸面過程反作用于氣候系統，進而影響流域的水文循環過程［１］ ，并將復合性結果表現于地表徑流過程。在降水稀少、生態脆弱的干旱半干旱地區，地表徑流過程尤為重要，其不僅關系沿岸地區的供水安全，也會影響地球關鍵帶的活躍程度，更是山水林田湖草沙生命共同體的重要紐帶，持續影響著旱區生態系統的健康狀況。已有研究表明，我國西北干旱半干旱地區地貌類型多樣，降水差異顯著，地表生態系統分異化明顯，這也導致區域水文過程及其形成機制具有很大的空間異質性［２］ ，因此科學認識西北旱區水文物理過程及水資源賦存與演化規律面臨極大挑戰。尤其是在西北旱區的無資料地區，水文過程定量估算不確定性所引發的水安全威脅，對國家的西部大開發、“一帶一路”建設以及鄉村振興重大戰略的實施都造成了重要影響。由此可見，探索西北干旱半干旱地區河川徑流演變規律及物理驅動過程至關重要，其對科學認識干旱半干旱地區水循環演化模式、保障區域水安全與生態安全、促進區域高質量發展意義重大。

一直以來，水文模型都被認為是提高對流域水文演化規律和物理驅動機制認識的重要手段，可將各類氣象水文數據與流域特征變量作為輸入，通過產匯流計算模擬或預測流域的徑流過程［３］ 。當模型參數未知時，一般可通過實際觀測數據對模型參數進行率定與校準，從而獲得模型參數值。而對無資料地區，則通常采用區域化關系來進行估計［４］ 。在干旱半干旱地區，基流是河川徑流的重要組成部分，也是非雨期河道徑流的主要來源，一般占河川徑流總量的５０％～８０％。很多干旱半干旱地區包氣帶較厚，且區域間入滲系數差異較大，使得區域基流過程與降水過程間存在較大的延遲，且多齡水特點突出，進而引發區域降水與徑流的相關關系不夠穩定，即很難保持單一的對應關系。而這一現象，也導致干旱半干旱地區降水—徑流模型校準時，因降雨形成基流的滯時高度多元性和地面徑流與基流耦合權重的高度不確定，使得很多水文模型在干旱半干旱地區的模擬效果欠佳［５］ 。而對于無資料地區，參證區域降水與徑流關系的非單一性導致區域水文過程與流域特征變量或參數間的統計關系無法有效建立［６］ ，無資料地區常用的水文比擬法也就缺少了科學基礎與依據。

近年來，很多學者聚焦于流域水儲量與流量的非線性關系，形成一種簡單且可廣泛應用的河道流量推求方法。已有研究表明，在很多流域應用非線性的水儲量—流量關系，可匹配更復雜的流量演算函數［７］ ，進而實現降水與徑流不穩定區域的流量過程估算。查閱文獻不難發現，很早就有對這種非線性關系的研究。早在１９４５ 年，Ｈｏｒｔｏｎ［８］ 就提出將流域出口流量與流域水儲量構建為冪函數關系，其包含兩個參數ａ、ｂ，分別表征流域尺度的土壤水力特性和地形的綜合效應，在理想狀況下，參數ａ、ｂ 可根據流域特征變量進行先驗估計而無須實測徑流進行校準。如Ｈｏｒｔｏｎ 在提出水儲量—流量冪函數關系的同時，確定了層流條件和湍流條件下ｂ 的取值。１９７７ 年，Ｂｒｕｔｓａｅｒｔ 等［９］ 又進一步估算了無承壓含水層中ｂ 的取值，并根據質量守恒定律以及鏈式法則，對原來的流域水儲量—流量冪函數方程進行了改進，提出了ＳＲＣ（Ｓｔｒｅａｍｆｌｏｗ ＲｅｃｅｓｓｉｏｎＣｕｒｖｅ），給出了ＳＲＣ 參數α、β 與Ｈｏｒｔｏｎ 水儲量—流量方程參數ａ、ｂ 之間的函數關系，ＳＲＣ 已成為目前應用非常廣泛的描述流域徑流衰退過程的方法。近年來，ＳＲＣ 持續發展，可實現利用流域徑流觀測值和流域特征變量估計無資料地區的ＳＲＣ 參數α、β 值，并作為一種廣泛使用的水文工具，集成在許多集總式水文模型中用來模擬徑流變化［１０］ 。有關學者陸續開展了ＳＲＣ參數α、β 的物理釋義與敏感性分析。如Ａｌｅｂａｃｈｅｗ等［１１］ 采用山坡模型，探討了ＳＲＣ 中α 和β 的關系，指出α 和β 對于地形坡度、表層土壤導水率和飽和導水率垂直衰減指數最敏感。Ｙｅ 等［１２］ 擬合了美國東部５０個流域的日流量衰退數據，進行了不同流域特征變量對α 和β 的敏感性分析，發現α 對土壤蓄水量、地表土壤飽和導水率敏感性表現強烈，而β 僅對干旱指數表現出敏感性。Ｍａｔｈｉａｓ 等［１３］ 聚焦英國１２０ 個流域的日流量衰退數據，結果發現α、β 與流域面積和基流指數均表現出較大的敏感性，且不同衰退數據篩選方法可能會影響α 與β 的取值。

黃土高原是我國干旱半干旱地區最大且最復雜的典型區，覆蓋面積占我國國土總面積的近７％。其位于我國西部大開發、“一帶一路”和生態文明建設的核心區，區內革命老區分布廣泛，也是我國鄉村振興的關鍵區，國家戰略意義顯著。近年來，在國家重大戰略的復合驅動下，黃土高原區的高質量發展持續向前推進，水土保持與生態保護成效顯著，高原變綠已成為震驚世界的盛景。然而，黃土高原區域特征顯著，具有獨特且多樣的地貌類型、稀少且異質的降水條件、脆弱且時變的生態環境、嚴重且廣泛的水土流失，諸多問題相互交織，使得黃土高原水安全備受威脅，也成為制約黃土高原區域高質量發展、保障國家戰略有效落地的障礙與挑戰。因此，研究黃土高原河川徑流演變規律及產匯流過程對提升區域水文過程演化及伴生影響的科學認知、有效開展黃土高原水安全保障與生態治理至關重要。然而，黃土高原降水少，潛在蒸發量大，包氣帶厚度可達８０ ｍ，這導致黃土高原的地表通量變化更趨復雜，降水向地表水、地下水的轉化存在較大的滯時和空間上的異質性，很難借助水文模型有效開展區域水文模擬與物理機制解析，相應地，流域特征參數的區域化賦值也無法有效定量。因此，從典型流域徑流ＳＲＣ參數的角度，認識流域特征變量與徑流衰退的關系，明晰ＳＲＣ 參數空間分布格局，并據此形成基于重力衛星反演數據的徑流過程推估方法，對認識黃土高原不同生態分區的水文演化特征和物理驅動機制、提供可靠的水文估算方法用于區域水資源規劃與生態安全保障意義重大。

為此，筆者基于黃土高原生態分區［１４］ ，選取皇甫、溫家川、綏德、延安、武山、秦安、吳旗、雨落坪、馬渡王和鸚鴿１０ 個水文站控制的典型流域為研究對象，對其流量衰退曲線數據進行空間分析，以探討不同生態區的ＳＲＣ 參數α、β 的空間演化特征。同時，建立ＳＲＣ 參數α、β 與可測量的流域特征變量（如地形、土壤特性、干旱指數、集水面積等）的回歸關系，以探究和驗證黃土高原流域特征變量對ＳＲＣ 參數α、β 的影響，進而實現對特征參數α、β 的區域物理釋義。最后，為驗證非線性水儲量—流量方程在黃土高原的適用性，基于ＳＲＣ 參數α、β 與Ｈｏｒｔｏｎ 方程參數ａ、ｂ 之間的函數關系，以ＧＲＡＣＥ 重力衛星反演陸地水儲量數據為輸入，估算不同流域的出口斷面流量，并驗證基于重力衛星反演數據推求河川徑流量方法的可行性，明確其在黃土高原的適用條件。

１ 研究區概況及數據來源

１．１ 研究區概況

黃土高原位于我國中部偏北的黃河中上游地區（北緯３３°—４１°，東經１０２°—１１４°），總面積約６４ 萬ｋｍ２。區域整體地勢西北高、東南低，海拔為８００～３ ０００ ｍ［見圖１（ａ）］，其中，西南區域起伏明顯［見圖１（ｂ）］。黃土高原主要位于干旱半干旱氣候區，干燥少雨，蒸發量大，具有典型的大陸性季風氣候特征，年降水量為１５０～７５０ ｍｍ，年水面蒸發量為１ ４００～２ ０００ ｍｍ［１５］ ，空間格局整體表現為西北較東南干旱，如圖１（ｃ）所示。區域水系以黃河為骨干，發源于黃土高原的河流較多，約有２００ 條，較大的有皇甫川、窟野河、無定河等。年河川徑流（不包括黃河干流）總量約１８５ 億ｍ３。

已有研究表明，黃土高原氣候類型多樣，自然地理條件復雜、空間組合變化明顯，水土流失與治理模式區域差異顯著［１６］ ，是我國典型的干旱半干旱區，也是我國生態治理與水安全保障的重點區。楊艷芬等［１４］ 參照國家發改委的分區方法，依據自然條件、水土流失治理技術和模式的區域性特征及差異，將黃土高原劃分為６ 個生態分區［見圖１（ｃ）］，即黃土高塬溝壑區（含Ⅰ區和Ⅱ區）、黃土丘陵溝壑區（含Ⅰ區和Ⅱ區）、沙地及農灌區、土石山區及河谷平原區。

１．２ 數據來源

降水數據來自黃土高原不同生態分區的１０ 個典型流域內及其周邊的眉縣、渭南、安定、華家嶺、準格爾旗、神木、麻黃山、吳旗、橫山、子長、米脂、莊浪、華池１３ 個氣象站（見圖１），日數據來源于中國地面氣候資料日值數據集（Ｖ３．０，ｈｔｔｐ：／／ ｄａｔａ．ｃｍａ．ｃｎ／ ），覆蓋時段與選用流域的徑流時段相同。潛在蒸散發量數據主要通過ＦＡＯＰｅｎｍａｎ－Ｍｏｎｔｅｉｔｈ 公式計算［１７］ ，逐日太陽輻射利用Ａｎ?ｇｔｒｏｍ－Ｐｒｅｓｃｏｔｔ 方程［１８］ 計算，計算中涉及的氣壓、風速、氣溫、相對濕度、日照時數等數據，亦來自中國地面氣候資料日值數據集（Ｖ３．０）。

ＤＥＭ 數據來源于國家地球系統科學數據中心黃土高原分中心（ｈｔｔｐ：／／ ｌｏｅｓｓ．ｇｅｏｄａｔａ．ｃｎ），分辨率為９０ ｍ；干旱指數來源于中國科學院植物科學數據中心（ｈｔｔｐｓ：／／ｗｗｗ．ｐｌａｎｔｐｌｕｓ．ｃｎ／ ）提供的第三版全球干旱指數和潛在蒸散數據庫中的１ ｋｍ 分辨率的干旱指數多年月平均數據［１９－２０］ ；土壤屬性數據來源于時空三極環境大數據平臺（ｈｔｔｐ：／／ ｐｏｌｅｓ．ｔｐｄｃ．ａｃ．ｃｎ）提供的面向陸面模擬的中國土壤數據集中的ＳＯＭ、ＳＡ、ＳＩ、ＣＬ、ＧＲＡＶ、ＰＯＲ 和ＣＥＣ的１ ｋｍ 分辨率數據，該數據將土壤深度分為８ 層，土層最深為２．３ ｍ［２１］ 。

ＧＲＡＣＥ 重力衛星反演水儲量數據采用了整合后的２００５—２０２０ 年空間分辨率為０． ２５° × ０． ２５° 的ＧＲＡＣＥ－ＦＯ 衛星數據，時間分辨率為１ 個月。由于衛星測量時電力不足、衛星震動和衛星更換，因此導致ＧＲＡＣＥ 重力衛星數據存在長短期數據缺失，為保證數據的連續性，采用三次樣條插值法對短期缺失數據進行插補［２２］ ，基于降水重建方法對長期缺失數據進行插補［２３］ 。

徑流數據選用了黃土高原不同生態分區１０ 條河流的控制水文站的徑流觀測數據，涉及皇甫站（皇甫川）、溫家川站（窟野河）、綏德站（大理河）、延安站（延河）、武山站（渭河）、秦安站（葫蘆河）、吳旗站（北洛河）、雨落坪站（馬蓮河）、馬渡王站（灞河）和鸚鴿站（石頭河），數據來源于黃河水利委員會印制的水文年鑒。

２ 研究方法

２．１ 水文時間序列的非一致性檢驗

在徑流時間序列的演變規律研究中，非一致性檢驗一直是水文時間序列分析首先要解決的問題，一般涉及趨勢變異檢驗、均值變異檢驗和方差變異檢驗等。為盡可能篩選人類影響較弱的近天然徑流序列，本研究采用了趨勢變異檢驗和均值變異檢驗來識別變異點的位置，進而刻畫徑流序列的非一致性特征。

Ｍａｎｎ－Ｋｅｎｄａｌｌ 趨勢檢驗法是一種基于樣本相互獨立假定條件下用于時間序列趨勢分析的非參數檢驗方法，其可通過兩個趨勢檢驗統計量ＵＦｋ 和ＵＢｋ 曲線在置信度線之間的交點判斷變異點。考慮到徑流數據之間可能存在自相關性［２４］ ，故本文采用了去趨勢預置白Ｍａｎｎ－Ｋｅｎｄａｌｌ（ＴＦＰＷ－ＭＫ）檢驗徑流時間序列的潛在變異位置。

Ｐｅｔｔｉｔｔ 均值變異檢驗法也是一種常用的變異檢驗方法，主要通過構建秩序列來識別水文序列的突變年份，并評價其顯著性［２５－２６］ 。本研究中，Ｐｅｔｔｉｔｔ 均值變異檢驗法同樣用于檢驗徑流時間序列的均值變異點，并與ＴＦＰＷ－ＭＫ 檢驗結果交叉驗證。

２．２ ＳＲＣ 分析

１９４５ 年，Ｈｏｒｔｏｎ 提出了一種流域水儲量與出口斷面流量的冪函數關系［８］ ，在本文中稱其為ＨＳＥ（ＨｏｒｔｏｎＳｔｏｒａｇｅ－Ｅｍｉｓｓｉｏｎｓ）方程。

ｑ ＝ａＶｂ （１）

式中：ｑ 為流域出口流量，Ｖ 為流域平均蓄水量，ａ、ｂ 為經驗參數。

１９７７ 年，Ｂｒｕｔｓａｅｒｔ 等［９］ 根據流域質量守恒及鏈式法則，對式（１）進行了改進，提出了ＳＲＣ。該曲線通過刻畫降水事件結束后河流流量的消退過程來解釋流域內部水文動態，已成為目前應用最廣泛的描述流域水文特征的方法。所提出的流量衰退（退水）公式如下。

式中：ｔ 為時間，ｑ 為日流量，α、β 為參數。

ＳＲＣ 參數α、β 與經驗系數ａ、ｂ 之間的關系為

為了構建衰退曲線，需要從所有觀測數據中篩選出衰退數據。為此，構建了流量梯度衰退流量Ｒｍ、響應流量Ｑｍ以及潛在凈徑流深Ｒｎｅｔ，計算方法如下。

式中：ｑ 為日流量，Ｐ 為日降水量，ＥＰＥＴ 為潛在蒸散發量，ｎ 為時間序列的第ｎ 天。

為了確保僅有衰退數據納入衰退回歸分析，需要排除Ｒｍ＜ω 和Ｒｎｅｔ ＜０ 的觀測值，其中ω 是與數值精度相關的閾值。根據２００６ 年Ｒｕｐｐ 等［２７］ 的研究結果，ω可被設置為每個流域Ｑｍ序列最小值的５ 倍。然后，利用式（２）取自然對數可得到式（８），離散化后，即可轉變為式（９）。最后，通過線性回歸，即可計算得到ＳＲＣ參數α、β。需要說明的是，回歸擬合中僅使用了變異點之前的序列數據，以減少人類活動對衰退分析產生的影響。

２．３ 流域特征值計算

１）潛在蒸散發量。ＦＡＯ Ｐｅｎｍａｎ－Ｍｏｎｔｅｉｔｈ（Ｐ－Ｍ）依據能量平衡和水汽擴散理論，提出了一種計算潛在蒸散發量的公式［１７］ 。

式中：Δ 為飽和水汽壓曲線的斜率，Ｒｎ為作物表面凈輻射，Ｇ 為土壤熱通量，γ 為溫度計常數，Ｔ 為２ ｍ 高處日平均氣溫，ｕ２為２ ｍ 高處的風速，ｅｓ為飽和水氣壓，ｅｎ為實際水氣壓。

逐日太陽輻射依據２００５ 年童成立等［２８］ 提出的計算方法獲得。而Ｐ－Ｍ 計算所使用的氣象要素值均來自于中國地面氣候資料日值數據集（Ｖ３．０）。

２）干旱指數。根據年降水量（Ｐ）和由Ｐ－Ｍ 公式計算得到的潛在蒸散發量（ＥＰＥＴ ） 可計算干旱指數ＩＡＩ［２９］ ，具體計算公式為

３）土壤屬性指數。面向陸面模擬的中國土壤數據集主要由第二次全國土壤普查的８ ５９５ 個土壤剖面制作而成，空間分辨率為１ ｋｍ。其將土壤數據分為８層［０，０．０４５）、［０．０４５，０．０９１）、［０．０９１，０．１６６）、［０．１６６，０．２８９）、［０． ２８９， ０． ４９３）、［０． ４９３， ０． ８２９）、［０． ８２９，１．３８３）、［１．３８３，２．２９６］，單位為ｍ。由于部分區域第７層與第８ 層土壤數據缺失，因此本文采用了前６ 層土壤數據。

首先，將土壤數據按流域邊界進行剪裁，并提取土壤孔隙度φ，土壤深度ｄ。而每層土壤的飽和導水率Ｋ則可通過將土壤數據中的陽離子交換率（ＫＣＥＣ）及各類物質占土壤質量的百分比［其中涉及砂粒（ＫＳＡ）、粉粒（ＫＳＩ）、黏粒（ＫＣＬ）、礫石（ＫＧＲＡＶ ）、有機質（ＫＳＯＭ ）］代入Ｓｐａｗ 軟件進行土壤屬性計算，進而得到每層土壤的平均飽和導水率Ｋｎ ，再根據每層土壤深度所占比重，計算空間平均飽和導水率Ｋ － 。

本文假設飽和導水率隨深度線性下降，即

Ｋｎ ＝Ｋ１ －ｆｄ （１２）

式中：Ｋ１ 和Ｋｎ 分別為第１ 層和第ｎ 層土壤飽和導水率，ｆ 為衰減參數。

得到土壤飽和導水率衰減參數計算公式為

然而，由于柵格類型參數（包括ｆ 在內）在空間上都是可變的，為了最小化不確定性，需要獲得流域尺度上更可靠的ｆ。文中使用柵格值估計了每一層土壤飽和導水率的空間算術平均值和空間平均深度，遂可將垂直衰減參數公式轉換為

式中：Ｋｎ為第ｎ 層土壤數據的平均飽和導水率，ｄ －為流域土壤深度的空間平均值。

通過將ｎ 層的土壤平均飽和導水率線性回歸擬合，即可實現求解。

２．４ ＧＲＡＣＥ 重力衛星數據估算流域出口流量

如前文所述，流域水儲量Ｖ 和流域出口斷面流量ｑ 的冪函數方程中的經驗系數ａ、ｂ 和ＳＲＣ 參數α、β 之間關系已建立，則可通過α、β 推求式（１）中的ａ、ｂ，即實現基于流域水儲量對流域出口斷面流量的推求。其中，每年的流域水儲量可通過實測數據和ＧＲＡＣＥ 衛星反演數據計算得到，具體計算公式如下：

Ｖ ＝Ｔ＋ΔＶＧＲＡＣＥ （１５）

式中：Ｔ 為２００２—２００９ 年流域水資源總量的多年平均值，ΔＶＧＲＡＣＥ為年際ＧＲＡＣＥ 重力衛星反演的水儲量變化量。

３ 結果分析

為了探究黃土高原地區ＳＲＣ 參數的空間異質性及其分布規律，明晰黃土高原ＳＲＣ 參數的物理釋義，分別對黃土高原不同生態區的１０ 個典型流域進行ＳＲＣ 分析，并將ＳＲＣ 參數的空間規律與流域特征值進行區域尺度的協同性分析，進而厘清ＳＲＣ 參數的空間分布格局及物理歸因。最后，選擇秦安站（葫蘆河）和武山站（渭河上游）為代表站，建立流域水儲量與出口流量的冪函數關系，并分析基于ＧＲＡＣＥ 重力衛星反演數據的ＨＳＥ 方程的估算效果。

３．１ ＳＲＣ 參數的空間特征

為更好地識別流域ＳＲＣ 參數α、β 的區域模式，同時避免氣候、地形以及陸面過程等空間組合變化的影響，在每一個生態分區選擇了兩個典型流域進行分析，如圖１（ｂ）所示，以期得到更為可靠的ＳＲＣ 參數α、β的分區規律。在時段的選擇上，依據Ｍａｎｎ－Ｋｅｎｄａｌｌ 趨勢變異檢驗和Ｐｅｔｔｉｔｔ 均值變異檢驗結果，結合不同潛在影響工程的建成或措施實施時間，確定不同典型流域的近天然時期：皇甫站１９６５—１９８２ 年，溫家川站１９７９—１９９６ 年，綏德站１９６０—１９７１ 年，延安站１９７９—１９９６ 年，吳旗站１９７９—１９９６ 年，雨落坪站１９６５—１９８２年，武山站１９７５—１９８９ 年，秦安站１９６５—１９８２ 年，馬渡王站１９７３—１９９０ 年，鸚鴿站１９７４—１９９１ 年。

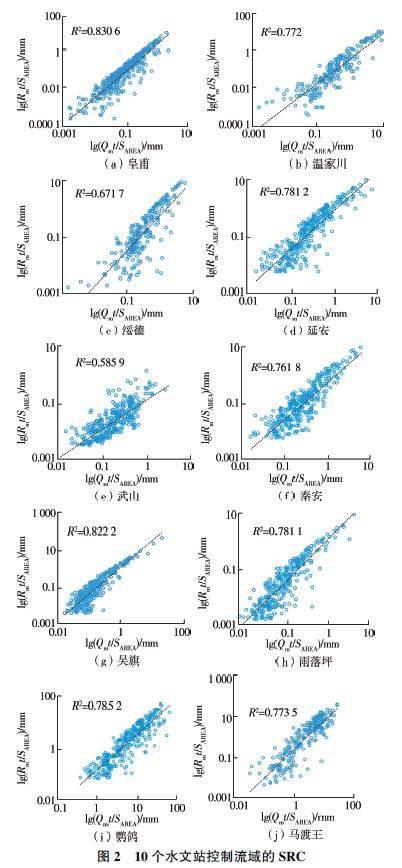
根據ＳＲＣ 的構建方法，首先從近天然期的觀測數據中篩選衰退事件和衰退數據。圖２ 中的點據即為已被歸類為衰退事件的衰退數據（Ｒｍ ＞ω 和Ｒｎｅｔ ＞０），各流域的數據規模在２５６～３２９ 個之間，僅為所有觀測數據的１／１０ 左右。然后基于衰退數據，按照式（９）逐流域進行ＳＲＣ 擬合，所得結果如圖２ 所示（ＳＡＲＥＡ 為集水面積），圖中虛線為線性擬合回歸曲線，即為ＳＲＣ。

將黃土高原不同生態區典型流域的ＳＲＣ 參數α、β 值繪于圖３。從中不難發現，在黃土高原地區，隨著緯度降低，β 值表現出整體增大的趨勢。而處于黃土高原緯度最低點的馬渡王站和鸚鴿站，與其他區域差異較大，并未延續空間上持續走高的態勢，而是參數β值相對較小。沿經度變化方向，β 值整體表現出自東向西不斷增大的趨勢，且在相近的經度區段內，如馬渡王站、綏德站、延安站β 值近似，且緯度相對較低的馬渡王站β 值略大于綏德站和延安站的，這與前面所提到的β 值隨緯度的變化規律是相符的。２０１３ 年，Ｙｅ等［１２］ 在對美國５０ 個流域進行ＳＲＣ 研究時發現，地形的陡峭會使α 值減小。在本文的分析中，也表現出類似的規律，如馬渡王站、鸚鴿站因靠近秦嶺北麓，地勢相對陡峭，這也解釋了馬渡王站和鸚鴿站ＳＲＣ 參數α值較小的原因。

聚焦ＳＲＣ 參數α 可知，緯度較低的秦安站、武山站、馬渡王站、鸚鴿站，其α 值均較小，而地處黃土高原中高緯度地區的雨落坪站、吳旗站、延安站、綏德站，α 值普遍偏大。但值得注意的是，黃土高原更高緯度的皇甫站、溫家川站α 值則相對較小，與武山站和秦安站相當，其原因需要進一步分析。

Ｂｒｕｔｓａｅａｒｔ 等［９］ 和Ｍａｔｈｉａｓ 等［１３］ 的研究表明，流域ＳＲＣ 參數α、β 一般與流域特征值具有很大的相關性，而對于同一生態分區而言，不同流域特征值的區域化綜合作用可協同驅動同一生態分區內流域ＳＲＣ 參數α、β 的變化。由圖３ 可以看出，在同一生態分區內，流域ＳＲＣ 的參數α、β 值相對穩定，空間異質性并不明顯，這也從側面證明了在黃土高原地區同一生態分區不同流域具有相似的水文驅動過程。

３．２ 基于流域特征的ＳＲＣ 參數物理釋義

表１ 列出了位于不同生態分區的１０ 個典型流域ＳＲＣ 參數α、β 與各類氣候、地貌和土壤水力特征的對比結果。主要涉及干旱指數（ＩＡＩ ）、集水面積（ＳＡＲＥＡ，ｋｍ２）、平均地形坡度（θ － ，°）、平均土壤埋深（ｄ，ｍ）、土壤孔隙度（φ，％）、土壤表層飽和導水率均值（Ｋ１，ｍｍ／ｈ）、土壤底層飽和導水率（Ｋ６，ｍｍ／ ｈ）以及土壤飽和導水率垂直衰減系數（ｆ）。圖４ 顯示了這些流域特征值與ＳＲＣ 參數α、β 之間的多維協同關系。

黃土高原影響水文過程因素繁多，物理驅動機制極其復雜，因此很難解釋某一流域特征值與ＳＲＣ 參數α、β 的一一對應關系，但仍可從表１ 和圖４ 發現部分流域特征值與參數α、β 間存在較強的關聯性。如在同一生態分區中，干旱指數ＩＡＩ（Ｒ２ ＝０．３１）和流域平均坡度θ（Ｒ２ ＝０．４０）對β 值的影響極為明顯，即干旱指數越小，β 值越大，而平均坡度越大，β 值越大。通過跨生態分區的分析，可以發現土壤平均飽和導水率Ｋ －與β 值的相關性較為明顯，Ｋ －越大的流域，其β 值越小，這也解釋了馬渡王站和鸚鴿站盡管干旱指數較小和平均坡度較大，但其β 值卻始終偏小的原因。

通過流域特征值與參數α 的相關性分析，可以發現土壤孔隙度φ（Ｒ２ ＝ ０．４１）、土壤飽和導水率垂直衰減系數ｆ（Ｒ２ ＝０．６９）與參數α 具有很強的同向或異向相關性，具體而言，φ 越大的流域參數α 值越大，而ｆ越大的流域α 值越小。對于土壤飽和導水率垂直衰減系數ｆ，參數α 表現出了較高的響應性特征，關聯程度位于所有流域特征值之首。

綜合以上分析，可以得到β 值與流域平均坡度和干旱指數具有較強的關聯關系，其中干旱指數與β 值成負相關關系，而流域平均坡度與β 值成正相關關系。參數α 值受土壤孔隙度和土壤飽和導水率垂直衰減系數的影響較大，其中，土壤飽和導水率垂直衰減系數與α 值成負相關關系，而土壤孔隙度與α 值成正相關關系。

３．３ 利用ＧＲＡＣＥ 重力衛星數據推估流域出口流量

根據２．４ 節所述方法，嘗試基于流域水儲量與流域出口流量的冪函數關系，利用ＧＲＡＣＥ 重力衛星反演的陸地水儲量（ＴＷＳＡ）數據推求流域出口斷面的流量過程。不同典型流域的估算結果表明，由于ＨＳＥ 方程僅建立了流域水儲量與流量之間的簡單冪函數關系，因此僅有流域水儲量變化相對平穩的秦安站和武山站獲得了較為合理的結果，由此可以證明流域水儲量借助冪函數方程推求流域出口流量僅適用于流域水儲量變化相對平穩的情況。

圖５ 顯示了秦安站和武山站控制流域ＧＲＡＣＥ 重力衛星反演多年月平均陸地水儲量（ＴＷＳＡ）變化量。

基于ＧＲＡＣＥ 重力衛星反演的陸地水儲量，借助ＨＳＥ 方程冪函數方程推算秦安站和武山站斷面的多年月平均流量，并將其與實測多年月平均流量一起繪于圖６ 中。由小提琴圖可知，估算結果與實測數據在多年平均尺度上較為近似，但估算結果相對集中，序列方差或者說波動明顯小于實測數據。從數據上看，秦安站和武山站的估算結果與實測數據分別分布在４～６ ｍ３ ／ ｓ和１２～１７ ｍ３ ／ ｓ 區間，這說明基于ＧＲＡＣＥ 重力衛星反演數據的估算方法在平水期應用效果較好，可在模擬或預測流域多年平均（徑）流量時使用。相反，在河流枯水期與汛期則估算效果較差，很難準確反映低水和高水變化。究其原因，可能與ＳＲＣ 參數在率定過程中取均值有關。

４ 結論

針對黃土高原地區降水稀少且潛在蒸散發強烈，生態環境脆弱且兼具時變性，包氣帶較厚且空間異質性大等多因素交織耦合導致黃土高原地區河川徑流演化復雜的問題，利用ＳＲＣ 法對黃土高原不同生態分區的１０ 個典型流域進行流量衰退分析，系統分析了ＳＲＣ參數α、β 的空間分布規律及與流域特征值間的相關關系，并進一步明晰了黃土高原流域ＳＲＣ 參數α、β 的空間分布格局與物理釋義。最后，以ＧＲＡＣＥ 重力衛星反演的陸地水儲量數據為輸入，驗證了Ｈｏｒｔｏｎ 所提出的水儲量數據推求出口斷面流量過程的冪函數方程（ＨＳＥ）在黃土高原的適用性。取得的成果和所得結論如下。

黃土高原同一生態分區的流域ＳＲＣ 參數α、β 具有穩定性。其中，β 值與流域所在的地理位置（即經緯度）有較好的相關關系，整體上緯度與β 成正相關關系，經度與β 成負相關關系。此外，β 值與流域平均坡度和干旱指數也具有較強的關聯性，其中干旱指數與β 成負相關關系，流域平均坡度與β 成正相關關系。參數α 與β 有所不同，其與地理位置并無較為明顯的關聯規律，而受土壤孔隙度和土壤飽和導水率垂直衰減系數的影響較大，其中土壤飽和導水率垂直衰減系數與α 成負相關關系，土壤孔隙度與α 成正相關關系。

Ｈｏｒｔｏｎ 所提出的基于流域水儲量推求出口斷面流量過程的冪函數規律在黃土高原是客觀存在的，可以利用ＧＲＡＣＥ 重力衛星反演的流域水儲量數據推求流域出口斷面流量，該結論已在秦安站和武山站控制流域的徑流模擬中得到了驗證。但這種冪函數規律具有一定的應用條件，即僅適用于流域水儲量變化較為平穩的流域。另外，研究還發現基于ＧＲＡＣＥ 重力衛星反演數據的推估結果在多年平均尺度上可以獲得與實測數據相近的結果，且趨勢一致，但對于低水和高水時段的估算效果則一般。因此，認為基于ＧＲＡＣＥ 重力衛星反演數據的流域出口流量過程估算方法可在模擬或預測流域多年平均（徑）流量時使用，可兼具便捷性與可靠性。

盡管本文在由ＧＲＡＣＥ 重力衛星反演的流域水儲量數據推求流域出口斷面流量方面做了一些有益的嘗試，但問題也客觀存在，如擬合結果在干旱期和汛期的響應欠佳，在流域水儲量數據不平穩的流域無法有效應用等，這無疑是下一階段需要重點破解的難題。

參考文獻：

［１］ ＫＯＳＴＥＲ Ｒ Ｄ，ＤＩＲＭＥＹＥＲ Ｐ Ａ，ＧＵＯ Ｚ Ｃ，ｅｔ ａｌ．Ｒｅｇｉｏｎｓ ｏｆＳｔｒｏｎｇ Ｃｏｕｐｌｉｎｇ Ｂｅｔｗｅｅｎ Ｓｏｉｌ Ｍｏｉｓｔｕｒｅ ａｎｄ Ｐｒｅｃｉｐｉｔａｔｉｏｎ［Ｊ］．Ｓｃｉｅｎｃｅ，２００４，３０５（５６８７）：１１３８－１１４０．

［２］ ＬＵ Ｓ，ＧＵＯ Ｗ Ｄ，ＧＥ Ｊ，ｅｔ ａｌ．Ｉｍｐａｃｔｓ ｏｆ Ｌａｎｄ Ｓｕｒｆａｃｅ Ｐａｒａｍ?ｅｔｅｒｉｚａｔｉｏｎｓ ｏｎ Ｓｉｍｕｌａｔｉｏｎｓ ｏｖｅｒ ｔｈｅ Ａｒｉｄ ａｎｄ Ｓｅｍｉａｒｉｄ Ｒｅ?ｇｉｏｎｓ： Ｔｈｅ Ｃａｓｅ ｏｆ ｔｈｅ Ｌｏｅｓｓ Ｐｌａｔｅａｕ ｉｎ Ｃｈｉｎａ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆＨｙｄｒｏｍｅｔｅｏｒｏｌｏｇｙ，２０２２，２３（６）：８９１－９０７．

［３］ 李彬權，牛小茹，梁忠民，等．黃河中游干旱半干旱區水文模型研究進展［Ｊ］．人民黃河，２０１７，３９（３）：１－４，９．

［４］ ＹＯＵＮＧ Ａ Ｒ．Ｓｔｒｅａｍ Ｆｌｏｗ Ｓｉｍｕｌａｔｉｏｎ Ｗｉｔｈｉｎ ＵＫ ＵｎｇａｕｇｅｄＣａｔｃｈｍｅｎｔｓ Ｕｓｉｎｇ ａ Ｄａｉｌｙ Ｒａｉｎｆａｌｌ?Ｒｕｎｏｆｆ Ｍｏｄｅｌ［Ｊ］．Ｊｏｕｒｎａｌｏｆ Ｈｙｄｒｏｌｏｇｙ，２００６，３２０（１－２）：１５５－１７２．

［５］ ＬＥＥ Ｈ，ＭＣＩＮＴＹＲＥ Ｎ，ＷＨＥＡＴＥＲ Ｈ，ｅｔ ａｌ．Ｓｅｌｅｃｔｉｏｎ ｏｆ Ｃｏｎ?ｃｅｐｔｕａｌ Ｍｏｄｅｌｓ ｆｏｒ Ｒｅｇｉｏｎａｌｉｓａｔｉｏｎ ｏｆ ｔｈｅ Ｒａｉｎｆａｌｌ?Ｒｕｎｏｆｆ Ｒｅｌａ?ｔｉｏｎｓｈｉｐ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２００５，３１２（１－４）：１２５－１４７．

［６］ ＷＡＮＧ Ｈ Ｊ，ＣＡＯ Ｌ，ＦＥＮＧ Ｒ．Ｈｙｄｒｏｌｏｇｉｃａｌ Ｓｉｍｉｌａｒｉｔｙ?ＢａｓｅｄＰａｒａｍｅｔｅｒ Ｒｅｇｉｏｎａｌｉｚａｔｉｏｎ Ｕｎｄｅｒ Ｄｉｆｆｅｒｅｎｔ Ｃｌｉｍａｔｅ ａｎｄ Ｕｎ?ｄｅｒｌｙｉｎｇ Ｓｕｒｆａｃｅｓ ｉｎ Ｕｎｇａｕｇｅｄ Ｂａｓｉｎｓ［Ｊ］．Ｗａｔｅｒ，２０２１，１３（１８）：２５０８．

［７］ ＭＣＩＮＴＹＲＥ Ｎ．Ａｐｐｏｒｔｉｏｎｉｎｇ Ｎｏｎ?Ｌｉｎｅａｒｉｔｙ ｉｎ Ｃｏｎｃｅｐｔｕａｌ Ｒａｉｎ?ｆａｌｌ?Ｒｕｎｏｆｆ Ｍｏｄｅｌｓ：Ｅｘａｍｐｌｅｓ ｆｒｏｍ Ｕｐｌａｎｄ ＵＫ Ｃａｔｃｈｍｅｎｔｓ［Ｊ］．Ｈｙｄｒｏｌｏｇｙ Ｒｅｓｅａｒｃｈ，２０１３，４４（６）：９６５－９８１．

［８］ ＨＯＲＴＯＮ Ｒ Ｅ．Ｅｒｏｓｉｏｎａｌ Ｄｅｖｅｌｏｐｍｅｎｔ ｏｆ Ｓｔｒｅａｍｓ ａｎｄ ＴｈｅｉｒＤｒａｉｎａｇｅ Ｂａｓｉｎｓ： Ｈｙｄｒｏｐｈｙｓｉｃａｌ Ａｐｐｒｏａｃｈ ｔｏ ＱｕａｎｔｉｔａｔｉｖｅＭｏｒｐｈｏｌｏｇｙ［Ｊ］．Ｂｕｌｌｅｔｉｎ ｏｆ ｔｈｅ Ｇｅｏｌｏｇｉｃａｌ Ｓｏｃｉｅｔｙ ｏｆ Ａｍｅｒｉｃａ，１９４５，５６（３）：２７５－３７０．

［９］ＢＲＵＴＳＡＥＲＴ Ｗ，ＮＩＥＢＥＲ Ｊ Ｌ．Ｒｅｇｉｏｎａｌｉｚｅｄ Ｄｒｏｕｇｈｔ ＦｌｏｗＨｙｄｒｏｇｒａｐｈｓ ｆｒｏｍ ａ Ｍａｔｕｒｅ Ｇｌａｃｉａｔｅｄ Ｐｌａｔｅａｕ［Ｊ］．Ｗａｔｅｒ Ｒｅ?ｓｏｕｒｃｅｓ Ｒｅｓｅａｒｃｈ，１９７７，１３（３）：６３７－６４３．

［１０］ ＴＡＳＨＩＥ Ａ，ＰＡＶＥＬＳＫＹ Ｔ，ＢＡＮＤ Ｌ Ｅ．Ａｎ Ｅｍｐｉｒｉｃａｌ Ｒｅ?ｅｖａｌｕａｔｉｏｎ ｏｆ Ｓｔｒｅａｍｆｌｏｗ Ｒｅｃｅｓｓｉｏｎ Ａｎａｌｙｓｉｓ ａｔ ｔｈｅ Ｃｏｎｔｉ?ｎｅｎｔａｌ Ｓｃａｌｅ ［ Ｊ］． Ｗａｔｅｒ Ｒｅｓｏｕｒｃｅｓ Ｒｅｓｅａｒｃｈ， ２０２０， ５６（１）：ｅ２０１９ＷＲ０２５４４８．

［１１］ ＡＬＥＢＡＣＨＥＷ Ｍ Ａ，ＹＥ Ｓ，ＬＩ Ｈ Ｙ，ｅｔ ａｌ．Ｒｅｇｉｏｎａｌｉｚａｔｉｏｎ ｏｆ Ｓｕｂ?ｓｕｒｆａｃｅ Ｓｔｏｒｍｆｌｏｗ Ｐａｒａｍｅｔｅｒｓ ｏｆ Ｈｙｄｒｏｌｏｇｉｃ Ｍｏｄｅｌｓ： Ｕｐ?Ｓｃａｌｉｎｇｆｒｏｍ Ｐｈｙｓｉｃａｌｌｙ Ｂａｓｅｄ Ｎｕｍｅｒｉｃａｌ Ｓｉｍｕｌａｔｉｏｎｓ ａｔ Ｈｉｌｌｓｌｏｐｅ Ｓｃａｌｅ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２０１４，５１９：６８３－６９８．

［１２］ ＹＥ Ｓ，ＬＩ Ｈ Ｙ，ＨＵＡＮＧ Ｍ Ｙ，ｅｔ ａｌ．Ｒｅｇｉｏｎａｌｉｚａｔｉｏｎ ｏｆ Ｓｕｂ?ｓｕｒｆａｃｅ Ｓｔｏｒｍｆｌｏｗ Ｐａｒａｍｅｔｅｒｓ ｏｆ Ｈｙｄｒｏｌｏｇｉｃ Ｍｏｄｅｌｓ： Ｄｅｒｉ?ｖａｔｉｏｎ ｆｒｏｍ Ｒｅｇｉｏｎａｌ Ａｎａｌｙｓｉｓ ｏｆ Ｓｔｒｅａｍｆｌｏｗ ＲｅｃｅｓｓｉｏｎＣｕｒｖｅｓ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２０１４，５１９：６７０－６８２．

［１３］ ＭＡＴＨＩＡＳ Ｓ Ａ，ＭＣＩＮＴＹＲＥ Ｎ，ＯＵＧＨＴＯＮ Ｒ Ｈ．Ａ Ｓｔｕｄｙ ｏｆＮｏｎ?Ｌｉｎｅａｒｉｔｙ ｉｎ Ｒａｉｎｆａｌｌ?Ｒｕｎｏｆｆ Ｒｅｓｐｏｎｓｅ Ｕｓｉｎｇ １２０ ＵＫＣａｔｃｈｍｅｎｔｓ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２０１６，５４０：４２３－４３６．

［１４］ 楊艷芬，王兵，王國梁，等．黃土高原生態分區及概況［Ｊ］．生態學報，２０１９，３９（２０）：７３８９－７３９７．

［１５］ 黎揚兵，張洪波，任沖鋒，等．基于ＴＲＭＭ 降尺度數據的渭河流域干旱時空演變特征與重心遷移規律研究［Ｊ］．華北水利水電大學學報（自然科學版），２０２３，４４（３）：１４－２４．

［１６］ 時明立，史學建，付凌，等．黃土高原淤地壩泥沙沉積的空間差異研究［Ｊ］． 人民黃河，２００８，３０（３）：６４－ ６５，８５，８８．

［１７］ ＡＬＬＥＮ Ｒ Ｇ，ＰＥＲＥＩＲＡ Ｌ Ｓ，ＲＡＥＳ Ｄ，ｅｔ ａｌ．Ｃｒｏｐ Ｅｖａｐｏ?ｔｒａｎｓｐｉｒａｔｉｏｎ?Ｇｕｉｄｅｌｉｎｅｓ ｆｏｒ Ｃｏｍｐｕｔｉｎｇ Ｃｒｏｐ Ｗａｔｅｒ Ｒｅ?ｑｕｉｒｅｍｅｎｔｓ?ＦＡＯ Ｉｒｒｉｇａｔｉｏｎ ａｎｄ Ｄｒａｉｎａｇｅ［Ｊ］．ＦＡＯ，１９９８，３００（９）：Ｄ０５１０９．

［１８］ 左大康，王懿賢，陳建綏．中國地區太陽總輻射的空間分布特征［Ｊ］．氣象學報，１９６３，２１（１）：７８－９６．

［１９］ＺＯＭＥＲ Ｒ Ｊ，ＸＵ Ｊ Ｃ，ＴＲＡＢＵＣＣＯ Ａ． Ｖｅｒｓｉｏｎ ３ ｏｆ ｔｈｅＧｌｏｂａｌ Ａｒｉｄｉｔｙ Ｉｎｄｅｘ ａｎｄ Ｐｏｔｅｎｔｉａｌ Ｅｖａｐｏｔｒａｎｓｐｉｒａｔｉｏｎ Ｄａｔａ?ｂａｓｅ［Ｊ］．Ｓｃｉｅｎｔｉｆｉｃ Ｄａｔａ，２０２２，９（１）：４０９．

［２０］ ＴＲＡＢＵＣＣＯ Ａ，ＺＯＭＥＲ Ｒ．Ｇｌｏｂａｌ Ａｒｉｄｉｔｙ Ｉｎｄｅｘ ａｎｄ ＰｏｔｅｎｔｉａｌＥｖａｐｏｔｒａｎｓｐｉｒａｔｉｏｎ （ＥＴ０） Ｃｌｉｍａｔｅ Ｄａｔａｂａｓｅ Ｖ２［Ｊ］．ＣＧＩＡＲＣｏｎｓｏｒｔ Ｓｐａｔ Ｉｎｆ，２０１８，１０：ｍ９．

［２１］ ＷＥＩ Ｓ Ｇ，ＤＡＩ Ｙ Ｊ，ＬＩＵ Ｂ Ｙ，ｅｔ ａｌ．Ａ Ｃｈｉｎａ Ｄａｔａ Ｓｅｔ ｏｆ ＳｏｉｌＰｒｏｐｅｒｔｉｅｓ ｆｏｒ Ｌａｎｄ Ｓｕｒｆａｃｅ Ｍｏｄｅｌｉｎｇ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ａｄ?ｖａｎｃｅｓ ｉｎ Ｍｏｄｅｌｉｎｇ Ｅａｒｔｈ Ｓｙｓｔｅｍｓ，２０１３，５（２）：２１２－２２４．

［２２］ ＨＵＭＰＨＲＥＹ Ｖ，ＲＯＤＥＬＬ Ｍ，ＥＩＣＫＥＲ Ａ．Ｕｓｉｎｇ Ｓａｔｅｌｌｉｔｅ?Ｂａｓｅｄ Ｔｅｒｒｅｓｔｒｉａｌ Ｗａｔｅｒ Ｓｔｏｒａｇｅ Ｄａｔａ： Ａ Ｒｅｖｉｅｗ ［ Ｊ］．Ｓｕｒｖｅｙｓ ｉｎ Ｇｅｏｐｈｙｓｉｃｓ，２０２３，４４：１４８９－１５１７．

［２３］ ＺＨＯＮＧ Ｙ Ｌ，ＦＥＮＧ Ｗ，ＨＵＭＰＨＲＥＹ Ｖ，ｅｔ ａｌ．Ｈｕｍａｎ?Ｉｎ?ｄｕｃｅｄ ａｎｄ Ｃｌｉｍａｔｅ?Ｄｒｉｖｅｎ Ｃｏｎｔｒｉｂｕｔｉｏｎｓ ｔｏ Ｗａｔｅｒ ＳｔｏｒａｇｅＶａｒｉａｔｉｏｎｓ ｉｎ ｔｈｅ Ｈａｉｈｅ Ｒｉｖｅｒ Ｂａｓｉｎ， Ｃｈｉｎａ ［ Ｊ］． ＲｅｍｏｔｅＳｅｎｓｉｎｇ，２０１９，１１（２４）：３０５０．

［２４］ 張洪波，李哲浩，席秋義，等．基于改進過白化的Ｍａｎｎ?Ｋｅｎｄａｌｌ趨勢檢驗法［Ｊ］．水力發電學報，２０１８，３７（６）：３４－４６．

［２５］ 張洪波，余熒皓，南政年，等．基于ＴＦＰＷ－ＢＳ－Ｐｅｔｔｉｔｔ 法的水文序列多點均值跳躍變異識別［Ｊ］．水力發電學報，２０１７，３６（７）：１４－２２．

［２６］ 黃強，孔波，樊晶晶．水文要素變異綜合診斷［Ｊ］．人民黃河，２０１６，３８（１０）：１８－２３．

［２７］ ＲＵＰＰ Ｄ Ｅ，ＳＥＬＫＥＲ Ｊ Ｓ．Ｉｎｆｏｒｍａｔｉｏｎ，Ａｒｔｉｆａｃｔｓ，ａｎｄ Ｎｏｉｓｅｉｎ ｄＱ／ ｄｔ?Ｑ Ｒｅｃｅｓｓｉｏｎ Ａｎａｌｙｓｉｓ［Ｊ］．Ａｄｖａｎｃｅｓ ｉｎ Ｗａｔｅｒ Ｒｅ?ｓｏｕｒｃｅｓ，２００６，２９（２）：１５４－１６０．

［２８］ 童成立，張文菊，湯陽，等．逐日太陽輻射的模擬計算［Ｊ］．中國農業氣象，２００５，２６（３）：１６５－１６９．

［２９］ ＡＲＯＲＡ Ｖ Ｋ．Ｔｈｅ Ｕｓｅ ｏｆ ｔｈｅ Ａｒｉｄｉｔｙ Ｉｎｄｅｘ ｔｏ Ａｓｓｅｓｓ ＣｌｉｍａｔｅＣｈａｎｇｅ Ｅｆｆｅｃｔ ｏｎ Ａｎｎｕａｌ Ｒｕｎｏｆｆ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２００２，２６５（１－４）：１６４－１７７．

【責任編輯 張 帥】

基金項目：國家自然科學基金資助項目（５２３７９００３，５１９７９００５）； 陜西省自然科學基礎研究計劃項目（２０２２ＪＣ－ＬＨＪＪ－０３）；中央高校基本科研業務費專項（３００１２２９３２０１）