邏輯推理素養培養視角下的高中數學課堂教學

王世瓊

摘要：培養學生的邏輯推理素養，既能夠助力學生對數學知識的有效掌握，也能夠幫助學生掌握推理技巧與推理方法.據此，筆者將從高中數學邏輯推理素養培養的基本原則與基本策略入手，闡述如何有效開展高中數學課堂教學.

關鍵詞：邏輯推理；高中數學；課堂教學

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）12-0047-03

邏輯推理素養是指，在教學中教師應從事實和命題處入手，根據相應的規則推理獲得其他命題的一種數學素養.在邏輯推理素養中，一般將其分為兩類：其一為“特殊到一般”推理，包括有歸納推理、類比推理；其二為“一般到特殊”推理，包括有演繹推理.

1 高中數學邏輯推理素養培養應遵循的基本原則

1.1 重視邏輯推理習慣的有效引導

在培養學生邏輯推理素養的過程中，教師也應重視對學生的引導，即給到學生一定的思路與啟發，由學生進行自主思考.只有這樣，學生才能真正具備邏輯推理能力.在教師的引導中，學生積極思考，努力整合所學知識，做到嚴謹推理過程，養成良好的推理習慣.

1.2 重視邏輯推理規律的清晰講解

在培養學生數學邏輯推理能力的過程中，教師需要重視對邏輯推理規律的清晰講解.對高中學生而言，高中數學知識具有一定的難度，要想實現對知識的深入理解，學生應扎實掌握基礎知識，在此基礎上，教師講解的邏輯推理規律才能夠被學生有效理解.因此，在高中階段的數學課堂中，要想實現對學生邏輯推理素養的培養，教師應

重視邏輯推理規律的講解，并在教學中有意識地引導學生厘清推理問題的內部邏輯.

1.3 尊重學生邏輯推理的發展需要

對學生而言，從小學到初中階段的學習，是其自身思維發展的重要過程，這是學生必須經歷的學習過程.而到了高中階段，學生的需求會增多，這是學生思維發展的需要，更是學生實現深入學習的必經之路.為此，教師應在教學中尊重學生的發展需要，努力講好關于邏輯推理的課程，讓學生掌握邏輯推理，并引導學生借此提高數學學習能力，努力豐富自己的知識和內涵.

2 高中數學邏輯推理素養培養應實施的基本策略

2.1 設置情境，認知邏輯推理

在認知邏輯推理內容的過程中，教師需要運用情境教學手段，為學生設置關于邏輯推理的教學情境，以此來引導學生正確認知邏輯推理.在此基礎上，教師實施的教學活動才是有效、有意義的.在設置教學情境時，教師可以結合學生的實際情況設置故事情境、生活情境、問題情境等不同形式的教學情境，從而實現對學生邏輯推理能力的有效認知[1].

以人教版數學必修第一冊第一章中《1.3 集合的基本運算》為例.在本章節的學習中，學生應借助對以下知識內容的學習，做到對邏輯推理的基本認知.具體如下：準確理解、掌握、運用交集、并集、全集、補集的知識，知曉不同集合之間的關系運算，從而實現對邏輯推理知識的初步認知.基于此，在教學實踐中，教師可以通過創設生活情境的方式，引出本次學習的知識內容.首先，了解并集與交集.教師可以展示生活中常見的標志：公共交通上的老弱病殘孕專座，并讓學生推理四種情況之間的關系.在推理分析中，學生可以從每個字所代表群體的具體含義入手，如“老”是指老人，“弱”是指弱小的兒童，“病”是指病人，“孕”是指孕婦.在知曉具體含義后，學生便能夠發現其中的集合關系，即這四類人是并集關系，只要滿足其中一個條件，便可以坐在該座位上.再如“多快好省”曾是國家建設的宣傳標語，現為許多商家使用的廣告語.在推理分析中，學生依舊需要從每個字的具體含義入手：“多”是指數量多，“快”是指速度快，“好”是指質量好，“省”是指成本省.但是，這四條標準之間的關系還是并集嗎？答案是否定的，這四條標準是交集關系，即需要同時滿足四條標準的要求，才能夠讓商家做到吸引消費者的目的.

在上述情境中，教師借助生活實例設置了教學情境，并引導學生對情境內容進行分析與推理，以此促進學生對并集與交集知識的掌握，并從集合知識中獲得對邏輯推理的初步認知，有效建立邏輯推理意識.

2.2 講解例題，感受邏輯推理

在數學課堂中，教師需要借助例題講解新知識、總結舊知識，讓例題成為新知識與舊知識之間的橋梁.因此，在邏輯推理的數學課堂上，教師需要借助對例題的講解，引導學生感受邏輯推理、理解邏輯推理.

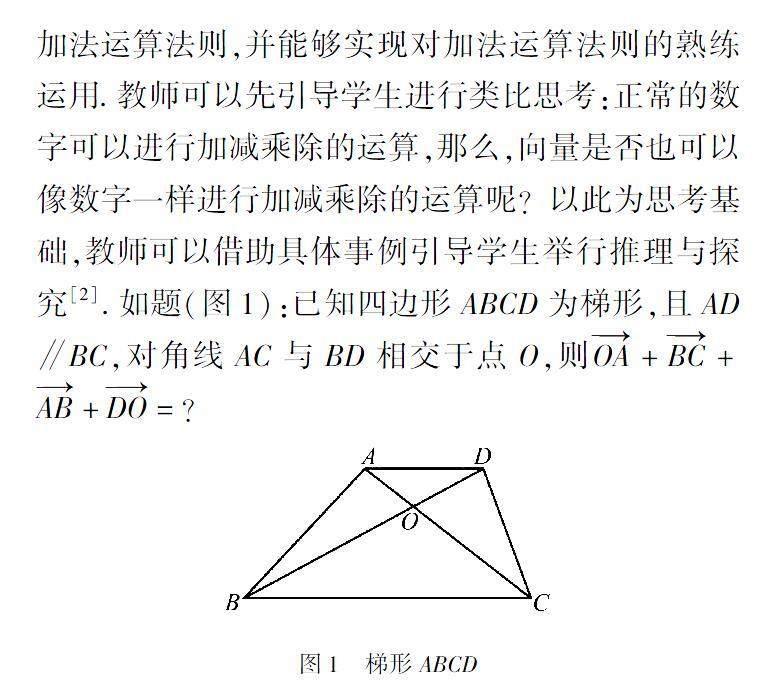
以人教版數學必修第二冊第六章中《6.2.1 向量的加法運算》為例.在本次課程的學習中，學生需要借助對實例與平面向量的幾何意義，掌握向量的加法運算法則，并能夠實現對加法運算法則的熟練運用.教師可以先引導學生進行類比思考：正常的數字可以進行加減乘除的運算，那么，向量是否也可以像數字一樣進行加減乘除的運算呢？以此為思考基礎，教師可以借助具體事例引導學生舉行推理與探究[2].如題（圖1）：已知四邊形ABCD為梯形，且AD∥BC，對角線AC與BD相交于點O，則OA+BC+AB+DO=？

在推理解決該問題時，教師要引導學生體會推理的過程，即向量與向量間的加法運算法則，具體計算推理過程如下：OA+BC+AB+DO =DO+OA+AB+BC=DA+AB+BC=DB+BC=DC.在本題的計算中，學生需要根據題目中提供的信息，找到不同向量之間的關系，如DO與OA是在△DOA中，而根據向量加法的三角形可知DO+OA=DA，如此便可以繼續根據向量加法的三角形法計算△DAB中涉及的向量關系，經過層層推導，獲得最終的結果.其實，解題的關鍵在于學生能夠充分理解向量加法的三角形法則，并根據法則完成向量之間的推導.

因此，在引導學生感受邏輯推理時，教師需要借助具體例題，為學生清晰地解釋每一個推理步驟的依據.這樣，學生在掌握習題的同時，對向量加法的三角形法則也能夠熟練掌握.2.3 設計問題，嘗試邏輯推理

在實際教學中，教師通過設計問題，引導學生對邏輯推理的問題進行思考，并嘗試自主解決邏輯推理問題.對學生而言，嘗試自己解決邏輯推理問題，不僅是對自身知識掌握情況的考驗，也是促進自身能力進步的重要途徑.學生需要依靠自己完成知識的獲取，這也是學生掌握邏輯推理能力的重要一步.因此，在教學中，教師應積極設計問題，引導學生進行邏輯推理.

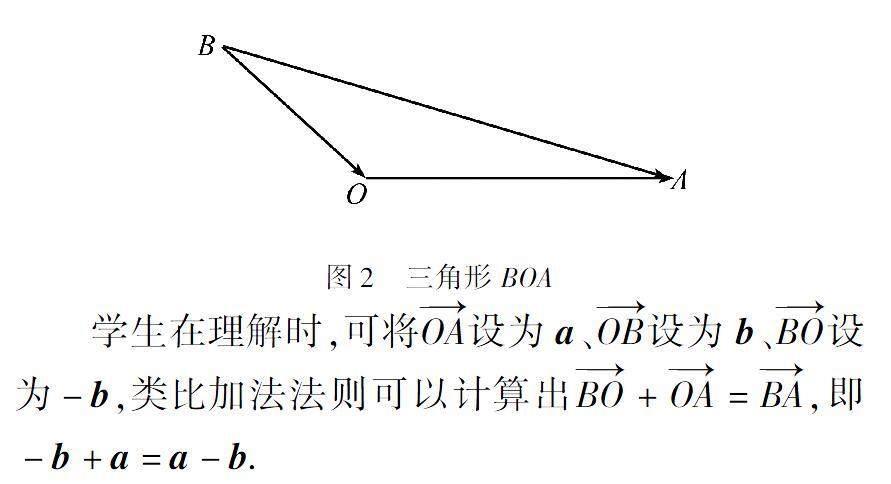
以人教版數學必修第二冊第六章中《6.2.2 向量的減法運算》為例.在本課程的學習中，學生應掌握相反向量的概念，理解并能夠運用向量減法的運算法則.對此，在上文學習向量加法的基礎上，教師可以借助問題的設計，引導學生自主思考，讓學生嘗試自主完成問題的推理與解決.首先，教師可以借助減法運算的知識，設置類比問題，如根據數的運算的減法法則，能否獲得向量的減法法則？如果能，應該怎樣定義呢？如何理解與運用向量減法的三角形法則？是否可以類比向量加法的三角形法則呢？其次，學生應對問題進行類比思考，并講出最后的答案.理解前兩個問題，需要清楚減法是加法的逆運算，即減去一個數等于加上這個數的相反數，類比推理可得“減去一個向量等于加上這個向量的相反向量”，如a-b= a+（-b），同理可以獲得向量減法的三角形法則.如圖2中所示：

學生在理解時，可將OA設為a、OB設為b、BO設為-b，類比加法法則可以計算出BO+OA=BA，即-b+a=a-b.

通過上述推理，學生便可以獲得關于向量減法的三角形法則，并能夠理解其蘊含的意義，進而在題目中熟練運用.

2.4 反思過程，把握邏輯推理

在邏輯推理的過程中，學生應對自己的推理過程有切實的把握，既要有邏輯推理的思路，也要有對邏輯推理過程的反思.只有這樣，學生才能在數學學習中真正掌握邏輯推理知識，實現對邏輯推理知識的有效運用.因此，在數學課堂上，教師應引導學生養成反思邏輯推理過程的習慣，在推理過程中做到嚴謹細致，以此來鍛煉自己的推理思維，實現對推理知識的有效運用，進而提升推理能力.

以人教版數學必修第二冊第六章中《6.2.1 向量的加法運算》和《6.2.2 向量的減法運算》為例.在上文的闡述中，筆者借助具體的實際案例，從為學生詳細講解向量的加法運算，到學生在教師的指點下自主完成加法運算的學習，不僅鍛煉了學生的學習能力，更重要的是讓學生學會進行知識的類比學習，能夠在一定邏輯思維的促進下，實現獨立自主的學習.但是，在學習向量加法與減法的過程中，學生需要對自己計算的內容、學習的知識進行及時的反思與總結，主動將思想向邏輯推理靠攏，這樣才能提升邏輯推理能力.在學習中，筆者認為，學生應將重點放在理解向量加法的三角形法則和向量減法的三角形法則.通過題目的練習，我們會發現，向量計算最終都會歸入三角形中，不論題目初始時的圖形是平行四邊形，還是梯形等其他圖形，都需要將最終的計算落實在三角形上.故而，學生在運用的過程中，應思考如何將題目給的信息與最后需要獲得的結果進行關聯，即充分運用向量加法與減法的三角形法則.

對此，教師應在教學中及時將上述知識內容與學生分享，并提醒學生注意計算的過程.這樣，學生在解題時，便可以圍繞三角形法則尋找解題思路，從而確保整個計算過程的嚴謹、細致，促進學生邏輯推理能力的提高.

3 結束語

綜上，邏輯推理素養是高中學生必須具備的一種數學核心素養，是其深入學習數學知識、提高數學思維能力的重要素養.因此，在文章中，筆者從設置情境、講解例題、設計問題、反思過程四個方面入手，闡述了高中數學邏輯推理素養應實施的基本策略.該策略的實施不僅可以讓學生具備邏輯推理素養，更重要的是可以培養學生養成運用邏輯推理的習慣，這對學生數學核心素養和數學綜合能力的提升有重要意義.

參考文獻：

[1] 張劉珊.邏輯推理素養培養視角下的高中數學課堂教學策略[J].高考，2022（27）：89-92.

[2] 楊海山.基于邏輯推理素養的高中數學課堂教學對策探析[J].數學學習與研究，2022（24）：26-28.

［責任編輯：李璟］