拓寬對函數的認識

田載今

函數作為刻畫變量之間相互聯系的數學模型，是近代數學中一個非常重要的基礎概念，本文在人教版八年級數學教科書中“一次函數”內容的基礎上，再介紹一些關于函數的知識，希望能幫助同學們拓寬對函數的認識．

一 函數的含義

不了解函數的人，往往誤以為函數是一種數的名稱，如同自然數、有理數、實數等．其實，函數不是“數”，而是變量之間的對應關系，函數的英文單詞“function”，也有“作用”“功能”和“運轉”的釋義，這些都與函數的含義相關．

宇宙萬物都始終處在運動之中，運動帶來變化．人們為了定量地研究這些變化，找出了各式各樣的變量．例如，月亮不停地繞地球轉動，在不同的日期它與地球之間的距離發生著變化，這里的日期和地月距離都是變量，在某些事物的變化過程中，每當一個變量x或一組變量（x1，x2，…，xn）取了確定的值時，另一個變量y都有唯一確定的值與之對應，這種對應關系叫作變量y對變量x或變量組（x1，x2，…，xn）之間的單值對應．例如，地月距離y與日期x之間存在單值對應關系：當x取2021年9月21日（中秋節）時，y約為3.88x105km；當x取2023年9月29日（中秋節）時，y約為3.62×105km．

變量之間具有的單值對應關系，反映了事物的變化規律．為了數量化研究變化規律，函數這個重要的數學工具應運而生，這標志著數學研究的主要對象由常量轉向變量，它使數學和其他學科的理論研究和實際應用，都發生了深刻的變化．

從16世紀至今，函數概念的形成有很長的發展過程．初中數學教科書中給出的函數定義為：在一個變化過程中，如果有兩個變量x與y，并且對于x的每一個確定的值．y都有唯一確定的值與其對應，那么我們就說x是自變量，y是x的函數，這里主要有兩層意思：（1）兩個變量互相聯系，一個變量變化時另一個變量也隨之發生變化；（2）函數與自變量之間是單值對應關系，自變量的值確定后，函數的值是唯一確定的．這個定義是以單值對應觀點對函數的簡單樸素的刻畫，今后隨著數學學習的深入，同學們還會見到函數定義的其他形式（如集合、映射、序對等觀點下的函數定義）．它們與單值對應觀點下的定義本質一致，只是描述得更深刻而已．

解：圖1（1）中，x取任一值時，動點P（x，y）的位置唯一確定，從而縱坐標y唯一確定，y對x是單值對應，因而v是x的函數．圖1（2）中，x取某些值（例如x=a）時，對應曲線上的多個點，它們有不同的縱坐標，y對x不是單值對應，因而y不是x的函數．

二 函數的元和次

如果變量y對另一個變量x單值對應，則y是一個自變量x的函數，它叫作一元函數：如果變量y對有n個變量的一組變量（x1，x2，…，xn）單值對應，則y是n個自變量x1，x2，…，xn的函數，它叫作n元函數．例如，設正方形的邊長為x，則它的周長y1=4x，面積y2=x2都是一元函數；設矩形的長為x1，寬為x2，則它的周長y1=2（x1+x2），面積y1=x1x2都是二元函數：設長方體的長為x1，寬為x2，高為x3，則它的表面積y1=2（x1x2+x2x3+x1x3），體積y2=x1x2x3都是三元函數．

如果一元函數能表示成關于自變量的多項式的形式，則多項式的次數（自變量的次數）即為函數的次數．例如，y=ax+b（a，b為常數，a≠0）是一次函數，y=ax2+bx+c（a，b，c為常數，a≠0）是二次函數，y=a0xn+a1xn-1+…+an-1x+an（a0，a1，…，an為常數，a0≠0）是n次函數．

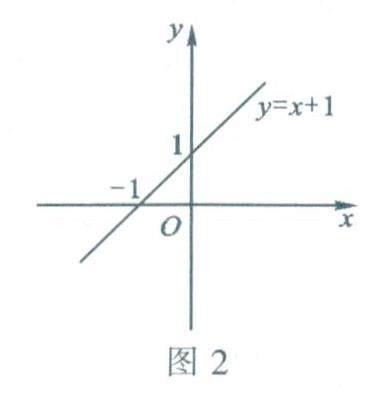
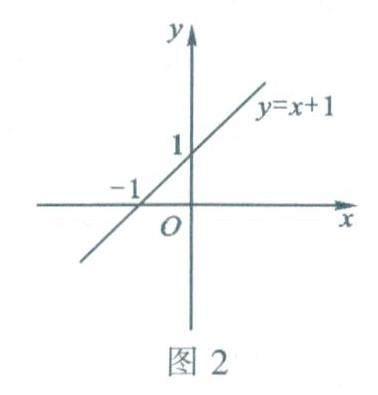
函數的表示法之一是圖象法，即通過點的坐標反映變量之間的對應關系．這種表示法將數量關系直觀形象地呈現出來，為數形結合研究問題提供了方便，在數學發展中有重要的作用．不同次數的一元多項式函數的圖象呈現為不同形狀的曲線，例如，圖2、圖3和圖4的三個函數圖象分別是一次函數y=x+1．二次函數y=x2+1和三次函數y=x3+1的圖象．一元多項式函數中，只有一次函數的圖象是直線，二次以上（含二次）函數的圖象都是非直的曲線，如二次函數y=x2的圖象是拋物線．因此，一次函數也叫作線性函數．

三 顯函數與隱函數

函數的本質是變量之間的單值對應．不論用什么形式，只要能表示這樣的對應關系，就可以表示函數．通常，表示函數用解析式、圖象、列表等方法，其中解析式最為常用，例如，圓的面積S=πr2是一元函數解析式（半徑r是自變量，S是函數，π是常數），圓錐的體積v=1/3πr2h，是二元函數解析式（自變量是底面半徑r和高h，V是函數，π是常數）．函數解析式中等號的左邊表示函數，右邊是關于自變量的算式．它不僅清楚地表示出哪個變量是函數、哪些變量是自變量，而且直觀地反映了函數與自變量之間的數量關系，即如何由自變量的值得出相應的函數值，因此，這種解析式叫作顯函數表達式．一元顯函數的解析式可簡寫為y=f（x）的形式，其中y是函數，x是自變量，符號f為function（函數）的首字母．n元顯函數的解析式可簡寫為y=f（x1，x2，…，xn）的形式，其中y是函數，x1，x2，…，xn是n個自變量．

多元方程是含有多個未知數的等式，如二元方程5x+y=1，3x2+2x-0.5y=6.雖然這兩個方程不是y=f（x）的形式，但是從它們可以分別推出y=-5x+1，y=6x2+4x-12這樣的一元顯函數，這就是說，這兩個方程各自隱含了一個函數，一般地，隱含了某種函數關系的方程，也叫作隱函數表達式．由此可知，函數與方程有著密切的聯系．

解：兩個方程都是隱函數表達式，它們分別對應一次函數y=4/3x-2與y=-2x+3.畫出這兩個函數的圖象（圖8），兩直線交于點（1.5，0），即x=1.5，y=0同時滿足兩個函數，也是兩個方程的公共解，這樣就用畫函數圖象替代了消元法的計算而得到方程組的解.

四 定義域和值域

五 一次函數圖像與直線

自變量為x的一次函數的形式為y=kx+b（其中k，b是常數，k≠0）．當b=0時，y=kx，又叫作正比例函數，一次函數y=kx+b的圖象也稱為直線y=kx+b.當x=0時，y=kx+b=6，由此可知，直線y=kx+b與y軸交于點（0，6）．6叫作直線y=kx+b在y軸的截距．如圖9，當k>0時，直線y=kx+b從左向右上升：當k<0時，直線y=kx+b從左向右下降．|k|越大，直線越“陡”，k的值決定直線y=kx+b的傾斜程度（包括傾斜的方向和陡緩）．k叫作直線y=kx+b的斜率．斜率和截距這兩個常數確定后，直線y=kx+b在坐標系中的位置就確定了．y=kx+b叫作直線的斜截式，它在解析幾何中常常用到．

需要注意，一次函數的圖象與坐標系中的直線并非一一對應關系，平行、重合于坐標軸的直線不是一次函數的圖象，它們對應的式子形如x=a或y=b，都不符合一次函數y=kx+b（k≠0）的形式．一次函數與坐標系中的不平行、不重合于坐標軸的直線有一一對應關系，即每個一次函數的圖象都是不平行、不重合于坐標軸的某條直線：反過來，每一條不平行、不重合于坐標軸的直線都代表某個一次函數的圖象．

把抽象的數量關系和直觀的圖象結合起來，從“數”與“形”兩方面動態地分析問題，對于全面認識函數有重要作用．例如，可以先從圖象發現k的符號和其絕對值對直線傾斜程度的影響；再進一步從解析式分析出當k>0（或k<0）時，如果x10），由此得出k對一次函數y=kx+b的增減性的決定作用．“數”與“形”結合，可以達到既直觀又入微的認識效果，這是研究函數的有效方法．