“三數一差”與圖表同行

張衛

平均數、中位數和眾數是反映一組數據集中趨勢的統計量，簡稱“三數”，方差反映了一組數據的波動大小，四者加起來簡稱“三數一差”，它們是數據分析的核心內容和重要指標，考查“三數一差”時，很多問題是通過圖表給出數據信息.

要求通過計算“三數一差”分析數據特征．

一 從統計表中提取數據

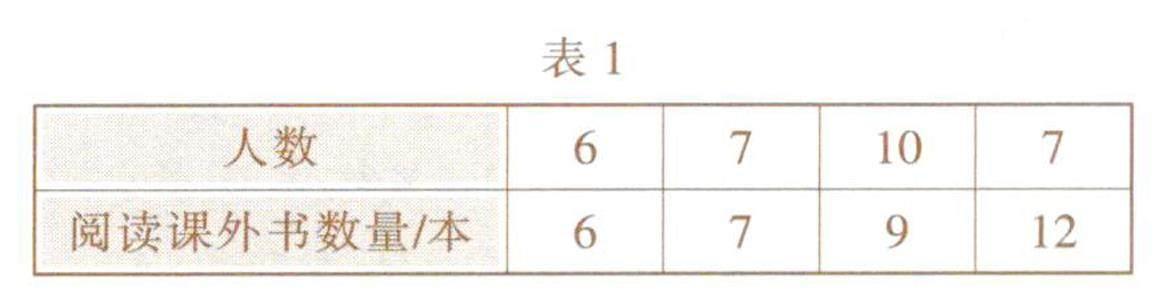
例1 （2023·棗莊）4月23日是世界讀書日，學校舉行“快樂閱讀，健康成長”讀書活動，小明隨機調查了本校七年級30名同學近4個月內每人閱讀課外書的數量，數據如表1所示．

閱讀課外書數量的中位數和眾數分別是（ ）．

A.8和9 B.10和9

C.7和12 D.9和9

解析：根據統計表所提供的信息，將統計表中的30個數據按照大小進行排列，可以發現處于最中間的第15個和第16個數據都是9，所以中位數為9+9／2＝9．這30個數據中，9出現10次，出現次數最多，所以眾數為9．故選D．

二 從扇形圖中分析數據

例2 八（1）班舉行投籃球比賽，每人投6次球，投進1球得1分．圖1是班上所有學生得分的扇形圖，下列關于班上所有學生得分的統計量的說法中，正確的是（ ）．

A.眾數為2 B.眾數為6

C.平均數為1.8 D.中位數為4

解析：眾數是出現次數最多的數據，對于扇形圖而言則是面積最大的扇形所對應的數據，可以看出，得2分的所占面積比例最大，所以眾數為2，A選項正確．由圖可知，將得分按從小到大的順序排列后，處于中間位置的數據應在3分區域內，因此中位數為3．根據各數據所占比例可求得平均數為0×100-10+2×35%+3×15%+4×20％+5×15%+6×5%=3．故選A．

三 從條形圖中整理數據

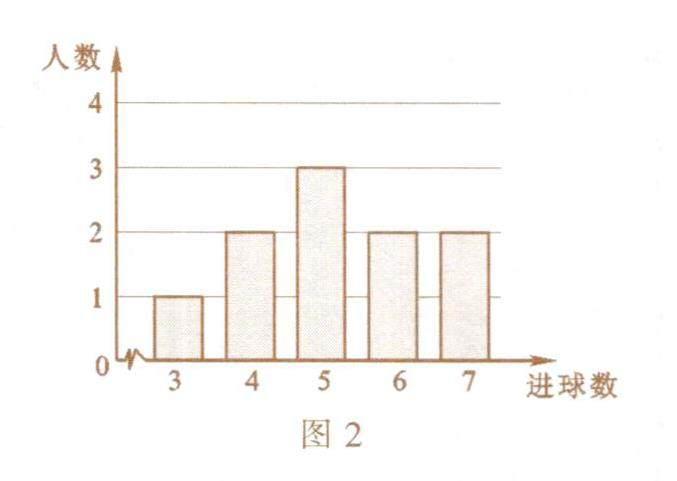
例3 為檢測學校足球隊的訓練效果，從隊中隨機抽取10名隊員進行射門檢測，進球數統計如圖2所示．對于這10名隊員的射門進球數，下列說法中錯誤的是（ ）．

A.中位數是5 B.眾數是5

C.平均數是5.2 D.方差是2

解析：從條形圖中分析數據時，眾數是最高的小長方形對應的數據，因此眾數是5．把這10名隊員射門進球數從小到大排列，排在第5和第6的數都是5，所以中位數是5．這10個數據的平均數是1／10×（3+4×2+5×3+6×2+7×2）=5.2，方差是1／10×[（3-5.2）2+2×（4-5.2）2+3×（5-5.2）2+2×（6-5.2）2+2×（7-5.2）2]=1.56.故選D．

四 從折線圖中觀察數據

例4 （2022·菏澤）射擊比賽中，某隊員的10次射擊成績（單位：環）如圖3所示，則下列結論中錯誤的是（ ）．

A.平均數是9 B.中位數是9

C.眾數是9 D.方差是0.8

解析：觀察折線圖可知，這組數據的平均數為1／10×（8.4+8.6+8.8+9+9+9+9.2+9.2+9.4+9.4）=9，中位數為9+9／2=9，眾數為9，方差為1／10×[（8.4-9）2+（8.6-9）2+（8.8-9）2+3×（9-9）2+2x（9.2-9）2+2×（9.4-9）2]=0.096．故選D.

試金石

1.小楠所在社會實踐小組的同學們到附近七個社區宣傳“垃圾分類”知識，他們記錄了各社區參與活動的人數，并制作了如圖4所示的折線統計圖，由統計圖可知，這組數據的眾數和中位數分別是（ ）．

A.42，40 B.42，38 C.40，40 D.38，42

2.八年級260名學生參加捐贈圖書活動．活動結束后隨機調查了部分學生每人捐贈圖書的數量，并按照捐贈圖書數量分為四種類型．A類：5本；B類：6本；C類：7本；D類：8本，最后，根據統計數據繪制了條形統計圖（圖5）和扇形統計圖（圖6）．

（1）本次調查獲取的樣本數據的中位數為________，在扇形統計圖中，m的值為________．

（2）求樣本數據的平均數．

（3）根據樣本數據估計這260名學生共捐贈圖書多少本．

（參考答案在本期找）