數據分析　創新中考

于秀埔

近年來，中考試卷中與數據分析有關的考題比較多，其中不乏具有創新性的題目．下面選取幾例進行分析，供同學們學習時參考．

一 不受影響的統計

例1 （2023·衢州）某公司5名員工在一次義務募捐中的捐款額（單位：元）為30，50，50，60，60．若捐款最少的員工又多捐了20元，則分析這5名員工捐款額的數據時，不受影響的統計量是（ ）．

A.平均數 B.中位數 C.眾數 D.方差

解析：由題意知，捐款最少的員工又多捐了20元，于是5個數據分別是50，50，50，60，60，則從小到大的順序不變，即中位數不變，而平均數、眾數、方差都要用到第一個數，故不受影響的統計量是中位數．選B．

二 沒有出現的數字

例2 （2023·杭州）將一枚質地均勻的正方體骰子（六個面分別標有數字1，2，3，4，5，6）投擲5次，分別記錄每次骰子向上的一面出現的數字，根據下面的統計結果，能判斷記錄的這5個數字中一定沒有出現數字6的是（ ）．

A.中位數是3，眾數是2

B.平均數是3，中位數是2

C.平均數是3，方差是2

D.平均數是3．眾數是2

解析：當中位數是3，眾數是2時，記錄的5個數字可能為2，2，3，4，6或2，2．3，5，6，故A選項不符合題意.

當平均數是3，中位數是2時，5個數之和為15，記錄的5個數字可能為1，1，2，5，6或1，2，2，4，6或2，2，2，3，6，故B選項不符合題意．

當平均數是3，方差是2時，5個數之和為15.假設6出現了1次，方差最小的情況下另外4個數為2，2，2，3，此時方差s2=1/5×[3×（2-3）2+（3-3）2+（6-3）2]=2.4>2．因此假設不成立，即一定沒有出現數字6，故C選項符合題意．

當平均數是3，眾數是2時，5個數之和為15.2至少出現2次，記錄的5個數字可能為1，2，2，4，6或2，2，2，3，6，故D選項不符合題意．

綜上，選C．

三 與遮蓋無關的統計量

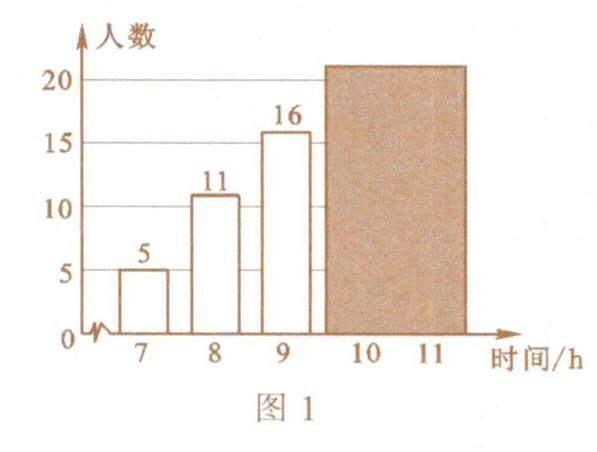
例3 （2022·南充）為了解“睡眠管理”落實情況，某中學隨機調查了50名學生每天的平均睡眠時間（時間均保留整數）．將樣本數據繪制成統計圖（圖1），其中有兩個數據被遮蓋，關于睡眠時間的統計量中，與被遮蓋的數據無關的是（ ）．

A.平均數 B.中位數 C.眾數 D.方差

解析：由統計圖可知，平均數無法計算，眾數無法確定，方差無法計算，而中位數是（9+9）÷2=9，與被遮蓋的數據無關．選B．