常用的幾個數據代表

田載今

研究問題時需要關注各種相關信息，這些信息通常以數字形式呈現，即統計中所稱的數據，數據不僅能簡潔地表達信息，而且能定量地刻畫信息，便于我們科學地分析信息，因而數據是研究問題的重要依據，隨著計算機和云計算的迅速發展，大數據時代已經到來，海量數據的處理得到越來越廣泛的應用．

統計學是研究數據處理的學科，統計的全過程包括：收集數據、整理數據、分析數據（發現并研究數據的分布特征），并依此推斷、評判已發生的事或預測將發生的事，在統計過程中，已收集到而未進一步處理的數據叫作原始數據．一般情況下，直接面對一組未經整理的原始數據，難以發現其分布特征．因此，通常需要對原始數據進一步加工整理，使其分布狀況變得清晰．從中得出相應的特征值作為數據代表，再從研究數據代表人手，深入研究相關問題．

一組數據的分布特征可以從不同方面進行分析，下面從數據分布的集中趨勢和離散程度兩方面，討論統計中常用的平均數、中位數、眾數和方差等數據代表．

一、描述集中趨勢的數據代表

“一組數據圍繞哪個中心數值分布？”這是分析數據時通常關注的一個問題．它關系到一組數據的平均水平或一般情況，對統計推斷有重要參考價值．在統計學中，把一組數據向某一中心數值靠攏的情形，稱為這組數據的集中趨勢．在描述數據的集中趨勢時，常從平均數、中位數和眾數中選擇合適的數據代表．

如果以一組數據大小的平均水平描述集中趨勢，則可用平均數作為數據代表．平均數由全部原始數據計算得出．如果以一組數據大小的中間水平描述集中趨勢，則可用中位數作為數據代表．一組數據按大小排列時，中位數在居中位置．如果以一組數據中出現次數最多的數據描述集中趨勢，則可用眾數作為數據代表，眾數是一組原始數據中出現次數最多的數據．一組數據的眾數可能有一個，也可能有多個，還可能一個也沒有，平均數、中位數和眾數各有各的作用，分別適合從不同角度分析數據的集中趨勢．

平均數是最常用的一個數據代表，它反映了一組數據大小的平均水平．需要注意的是，如果一組數據中有極端數據，即與多數數據相比過大或過小的個別數據，則它會使平均數的值與多數數據存在較大差距．如仍以平均數代表該組數據的中心數值，則不能恰如其分地反映這組數據的分布狀態．這種情形下，選擇中位數或眾數作為數據代表，能更好地反映一組數據的集中趨勢．

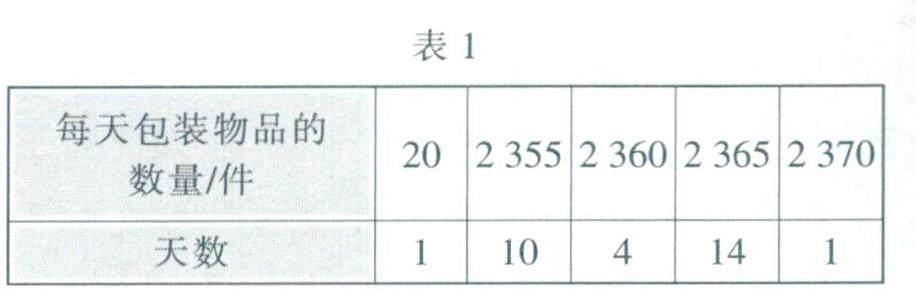
例1 表1為一條自動包裝線某月每天包裝物品的數量及相應的天數．

（l）分別求出表中數據的平均數、中位數和眾數．

（2）用平均數作為數據代表，能客觀反映這個月每天包裝物品數量的一般情況嗎？

解：（1）通過計算加權平均數，得表中數據的平均數為

（20+2355×10+2360×4+2365×14+2370）÷30=2283.

表中共有30天的數據，這30個數據從小到大排列時，處于正中間位置的第15和第16兩個數據的平均數為（2360+2365）÷2=2362.5．因此2362.5是該組數據的中位數．

30個數據中，2365出現14次，出現次數最多，因此2365是該組數據的眾數．

（2）觀察表中數據不難發現，30天中有29天的數據都不小于2355，它們都大于平均數，且與平均數的差都不小于72．這30天中有1天的數據20遠小于平均數2283，這可能是某一天自動包裝線有突發故障造成的反常結果，顯然，20這個極端數據，使得正常情況下應有的平均數的值變小．如果仍以平均數2283作為數據代表，則與自動包裝線每天工作的一般狀況差距較大．而以中位數2362.5或眾數2365作為數據代表，則能較客觀地反映一般情形下包裝物品數量的實際情況．因此，此問題不宜用平均數作為數據代表描述數據的集中趨勢．

二、描述離散程度的數據代表

“一組數據中，各個數據與這組數據的中心數值（例如平均數）的偏離程度有多大？”這是分析數據時通常關注的另一個問題，在統計學中，把這種偏離程度稱為這組數據的離散程度（或離中程度），它反映了一組數據大小的波動狀態．我們結合下面的問題對數據離散程度予以說明．

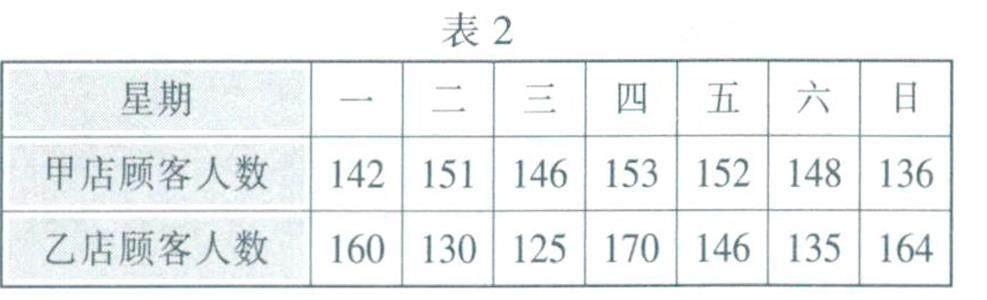
表2是某一周內甲、乙兩個書店接待顧客人數的記錄．

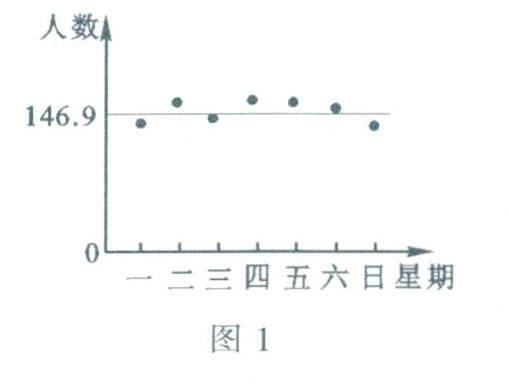
計算可知，甲、乙兩個書店該周內平均每天接待顧客人數分別約為146.9和147.1．兩者非常接近，我們再考慮兩組數據的波動狀態．先觀察數據散點圖，圖1和圖2中的點分別表示甲、乙兩個書店的顧客數量，各點的橫坐標為時間（星期一到星期日），縱坐標為顧客人數．圖中的水平線與縱軸交點的縱坐標是7個數據的平均數．

比較兩圖，直觀上可以發現：圖1中各數據點分布較緊密，波動較小，即總體上看各點與平均值對應的水平線的偏離度較小：圖2中各數據點分布較松散，波動較大，即總體上看各點與平均值對應的水平線的偏離度較大．這里的偏離度是對7個點偏離度的平均水平而言，是根據各數據點與平均數直線的距離大小而得出的．盡管與平均數直線相比，有些數據點高，有些數據點低，但各點與直線的距離都是非負的值．即高度差的絕對值，兩組數據相比，甲店數據的離散程度較小，乙店數據的離散程度較大．

統計學中常用方差對一組數據的波動情況（即各數據與平均數的偏離狀態）作定量的刻畫，描述數據的離散程度．計算方差的方法為：（1）計算一組數據的平均數；（2）計算各數據與平均數之差的平方和；（3）用所得平方和除以這組數據的個數．設一組數據為x1，x2，…，xn（共n個），記其平均數為x，方差為s2．則

例2 分別計算上面問題中甲、乙兩個書店某一周接待顧客人數的方差．南所得方差你能看出哪種可能性？

解：由以上所述可知，甲、乙兩個書店某一周平均每天接待顧客人數分別為146.9和147.1（保留到0.1）．計算兩組數據的方差，得甲店數據的方差s2甲=32.1，乙店數據的方差sz=272.1．比較兩個方差，得S2甲．

為什么計算方差要用各數據與平均數之差的平方和，而不直接把各數據與平均數之差相加呢？一般情形下，一組數據中可能有些數據比平均數大，有些數據比平均數小．它們與平均數之差會有正有負，如果直接把這些差相加，就會出現正負相抵．例如，一組數據為1，2，3，4，5，平均數為3，各數據與平均數之差分別為-2，一1，0，1，2．這些差之和為0，但這并不意味著這組數據都是緊靠著平均數的，用各數據與平均數之差的平方和，則利用了平方的非負性，防止出現做加法時正負相抵而隱藏了相關數據對平均數的偏離，方差名稱中的“方”正是“平方”的簡稱．

對方差的算式進行恒等變形：

這給出了方差的另一種算法：各數據平方的平均數減各數據平均數的平方．

從上面幾例可以看出，得出平均數、中位數、眾數和方差這四種常用數據代表的方法不同，這些數據代表所表示的意義也不同，在反映一組數據的分布特征時，它們有各自的側重點．根據實際問題的需要，選取合適的數據代表來認識一組數據的集中趨勢與離散程度，是分析數據的常用做法．