織機車間直捻機筒紗抓取機械臂逆運動學求解方法研究

于俊康 江維 李紅軍 陳偉 陳振

摘 要：紡織車間中通過協作機械臂代替工人實現對直捻機筒紗的自動更換，可降低工人勞動強度，提高筒紗卷繞的生產效率。在對機器人進行運動學建模與分析時，逆運動學求解是機器人運動學中關鍵部分。傳統法求機器人逆解存在求解速度慢、求解過程復雜、結果穩定性差等問題，采用傳統BP（Back Propa- gationg Neural Network）神經網絡求解又容易陷入局部極小值，針對上述問題，提出一種基于PSO優化算法（Particle Swarm Optimization Algorithm）的BP神經網絡機械臂逆運動學求解方法，通過PSO算法對BP神經網絡的權值和閾值進行多次迭代優化，避免了局部最小值的問題，提高了神經網絡的全局搜索能力。采用 D-H法建立機器人運動學模型，根據機器人正運動學方程由關節角度解得末端位姿，將解得結果作為數據集，通過學習算法經多次迭代確定神經網絡的模型參數，并對神經網絡進行性能檢驗。實驗結果表明： PSO-BP神經網絡相比于傳統的BP神經網絡收斂速度快，該模型在搬運機器人逆運動學求解中精度高，滿足紡織車間直捻機筒紗抓取作業的需要。

關鍵詞：紡織車間；直捻機；筒紗卷繞；機械臂逆運動學；PSO-BP神經網絡

中圖分類號：TP242?? 文獻標志碼：A? 文章編號：2097-2911-（2024）01-0021-12

Study on the Inverse Kinematic Solving Method of Grasping Mechanical Arm in Loom Workshops

YU Junkang a， JIANG Weia， b*， LI Hongjuna， CHEN Weia ， CHEN Zhena， b

（Wuhan Textile University a. School of Mechanical Engineering and Automation;

b. Hubei Provincial Key Laboratory of Digital Textile Equipment， Wuhan 430200， China）

Abstract：In the textile workshop， the automatic replacement of cylindrical yarn packages on the twisting ma- chine is achieved by using a collaborative robotic arm instead of human workers. It can reduce the labor intensi- ty of workers and improve the production efficiency of winding yarn packages. In the process of modeling and analyzing the robot's motion， the solution to inverse kinematics is a critical aspect of robot kinematics. Tradition- al methods for solving the inverse kinematics of robots suffer from issues such as slow computation speed， com- plex solving processes， and poor stability of results. Utilizing the traditional Back Propagation Neural Network （BPNN） for solving also tends to get stuck in local minima. To address these challenges， this paper proposes a method for solving the inverse kinematics of a robotic arm based on the Particle Swarm Optimization Algorithm （PSO） optimized Backpropagation （BP） neural network. Through multiple iterations using the PSO algorithm， the weights and thresholds of the BP neural network are optimized， preventing it from getting stuck in local min- ima and enhancing its global search capabilities. The robot's kinematic model is established using the Denavit- Hartenberg （D-H） method， and the end-effector pose is obtained by solving joint angles through the robot's for- ward kinematic equations. The results obtained serve as a dataset， and the model parameters of the neural net- work are determined through multiple iterations using a learning algorithm， followed by performance testing. Experimental results indicate that the PSO-BP neural network converges faster compared to the traditional BP neural network. The model exhibits high precision in solving the inverse kinematics of the material handling ro- bot， meeting the requirements for yarn-grabbing operations in the textile workshop.

Keywords： loom workshop；twisting machine；winding yarn packages；inverse kinematics of the robot arm； PSO-BP neural network

中國是紡織生產大國，紡織技術在國民經濟、生產、生活中占據重要地位。直捻機是一種重要的紡織裝備，其功能是將兩根原絲加捻后合并一起形成紗線，再對紗線進行卷繞操作形成筒紗，最后取下直捻機上卷繞好的筒紗進行染色。傳統的筒紗取放依靠人工，對于大型紡織車間，該方式效率低、勞動強度大，亟需開發一款能夠輔助甚至替換人工進行筒紗抓取作業的智能化裝備，因此，研究開發織機車間直捻機筒紗抓取智能裝備具有重要理論意義與實際應用價值[1-2]。利用 AGV搭載機械臂輔助甚至替換人工實現織機車間直捻機筒紗自動抓取是一種行之有效的手段[3-4]， AGV到達作業點后，機械臂抓取筒紗過程中需要通過各關節協調運動，在固定的坐標系中，抓取筒紗其實質是由目標抓取點反推機械臂各關節運動參數的過程即機械臂的逆運動學問題[5]。機器人正運動學求得的位置和姿態是唯一確定的，而逆運動學求得的各關節角度通常有多個解或有不存在解的可能，甚至會出現奇異解[6]，因此在抓取機械臂眾多逆解中尋求一組最優解以保證機械臂實現高性能抓取就顯得至關重要。

對機器人各關節求逆解是機器人運動學中重要的一步[7]，傳統的機器人逆運動學求解有代數法、幾何法和數值解法。幾何法是根據機械臂各桿件的平面幾何關系和三角學原理求解各關節角度[8]。如盧喆等[9]中針對六自由度機器人求解復雜、幾何定義模糊等問題[10]，對前3個軸線不相交的關節采用幾何法求解，后3個軸線交于一點的關節采用Paden-Kahan子問題的插值法進行求解，但對高維、非線性的方程組求解時，存在計算效率低、難度大的問題。數值解法是通過數值逼近、差值或有限元計算來求得一組滿足運動學方程的近似解。如林貞國[11]通過對偶矩陣的方法來求逆解，但該方法求解的難度較大，計算時間長，無法得到所有解，不適于實時性要求高的場合。代數法在運算速度和精度上有了較大的提升，但推導過程復雜，且機器人必須滿足Piper 準則[12]（即六關節機器人中有三個連續關節的軸線交于一點或相互平行）才能使用該方法。人工智能的發展為機器人逆運動學求解提供了新的思路[13]。最常見的是利用BP神經網絡[14]和RBF 神經網絡[15]求逆解，如陳平等[16]采用權值優化后的 RBF 神經網絡，來對機器人運動學求逆解。楊萍等[17]通過含有兩個隱含層的BP神經網絡對機器人求逆解。但當處理的數據較多時就會降低網絡的運算速度。有專家提出基于智能優化算法提高神經網絡的運算性能。如石建平[18]提出一種基于改進的克隆選擇算法來對機械臂運動學求逆解，該方法下種群多樣性的保持能力強，能夠處理常規法無法解決的冗余機械臂逆運動學求解問題。董云等[19]將傳統的解析法與遺傳算法相結合，提高了全局尋優能力使機械臂在運動過程中保持良好的穩定性和避障性能。陳睿等[20]采用競爭的多變異策略差分進化算法分別對局部和全局種群進行參數標定，提高了三自由度并聯機器人的運動精度。

綜上所述，本文提出一種PSO優化BP神經網絡的機器人逆運動學求解方法。PSO算法是基于群體智能的優化算法[21-22]，通過群體粒子間的合作與競爭搜尋最優解，該算法計算速度快、全局搜索能力強。通過PSO算法優化BP神經網絡權值和閾值，改善網絡結構，解決了BP神經網絡易陷入局部極小值的問題，提高了網絡的泛化性能和訓練速度。將優化后的PSO-BP神經網絡算法應用到紡織車間筒紗裝卸六自由度機械臂上，實驗結果表明，PSO-BP 神經網絡比傳統的 BP神經網絡得到的運算結果精度更高，改進后的神經網絡輸出結果的均方根誤差為0.071，且誤差波動小，為大型織機車間多自由度機械臂逆運動學求解及作業控制提供了新的思路。

1 紡織車間協作機器人運動學建模與分析

1.1 機器人結構與作業流程

全自動紗筒更換的智能紡織系統包括直捻機、協作機械臂、末端夾爪、自動牽引車（AGV）和物料箱如圖1所示，協作機械臂安裝于AGV上，該機械臂系統是一個6-DOF機構，各關節依次為旋轉關節、俯仰關節、俯仰關節、旋轉關節、旋轉關節、旋轉關節，末端執行器，用來抓取紗筒，以完成對直捻機或倍捻機上紗筒的更換。牽引車后搭載的物料車用來存放筒紗和空紗管。

當直捻機某一工位的紗筒卷滿紗線時，控制終端就會向機器人發送作業指令，AGV 接收到指令后通過地磁導引線牽引物料車移動到待作業位置，此時的機械臂處于初始狀態。機器人到達作業位置，通過機械臂各關節的配合完成末端與筒紗的初始定位，末端夾爪取下筒紗，并放置在物料箱內，再通過各關節的配合將空紗管安放在工位上，此時已完成對一個工位上紗管的更換。AGV 繼續移動到下一個待作業工位，重復上述操作，直到完成整個車間作業為止，其完整的操作流程如圖2所示。

1.2 機械臂連桿坐標系建立

建立筒紗抓取機械臂各關節坐標系，如圖3所示，獲得各連桿之間的相對運動和位姿關系。通過改進D-H法描述機械臂各連桿坐標系之間的關系，其中各關節均繞Z軸旋轉，α為坐標系繞X軸旋轉的角度，a 為連桿長度，d 為連桿關節偏移量，θ為坐標系繞Z軸旋轉角度。

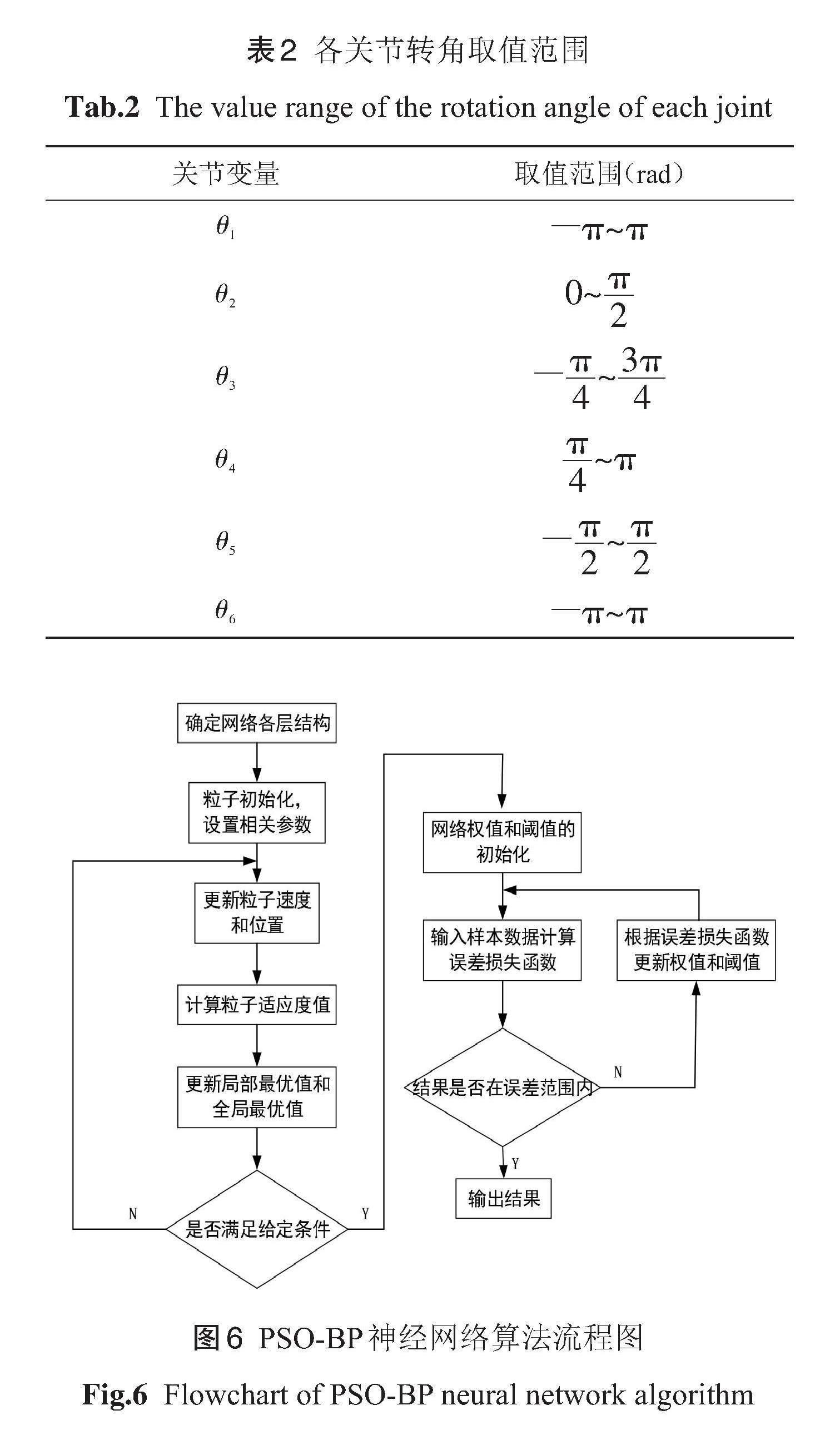
最終，得到協作機械臂 D-H 參數表，如表1所示。

1.3 機械臂正運動學推導

將表1中機械臂 D-H 參數帶入相鄰桿件坐標系的位姿變換矩陣，得到相鄰連桿之間的變換矩陣 i（i）?1T（i =1，2，3，4，5，6），如公式（1）所示。

公式（1）中：Cθ表示 cos θ ， Sθ表示 sin θ。根據機器人正運動學，將公式（1）相鄰桿件齊次變換矩陣依次左乘可得到機器人基坐標與機器人末端的位姿變換，即機械臂的齊次變換矩陣如公式（2）。

公式（2）為機器人運動學正解，其中 R =[nx，ox，ax ; ny ，oy ，ay ; nz ，oz ，az]表示機器人末端執行器的姿態，P =[px，py ，pz]為機器人末端的坐標位置，并以機器人末端的位置和姿態參數作為機械臂操作空間的數據集。按 z?y?z 軸的旋轉順序對姿態 R 進行歐拉變換得到偏轉角γ、俯仰角β、回轉角α ， 如公式（3）所示，與 px、py、pz 組成包含6個變量的數據集，作為 BP 神經網絡的輸入量，經神經網絡模型的運算得到機械臂各關節的角度θi （i =1， 2， 3， 4， 5， 6）。

α= ATAN2（ay ， ax）

β= ATAN2（ax cos α+ ay sin α， az）? （3）

γ= ATAN2（-nx sin α+ ny cos α， oy cos α-ox sin α）

公式（3）中ATAN2表示反正切函數，完整形式為：ATAN2（sin，cos），括號內依次為角度的正弦值和余弦值。

2 織機車間機械臂BP神經網絡逆解求解方法

2.1 BP神經網絡基本原理

BP神經網絡是一種根據誤差信號反向傳播和BP算法訓練的多層前饋型神經網絡，具有良好的非線性擬合能力，可應用于多輸入多輸出的非線性系統。該網絡結構由三層區域組成，各區域均含有多個神經元，每個神經元可將外部輸入或上一神經元的輸出作為該神經元的輸入信號，不同的輸入信號經過加權處理后進行累加，通過激活函數得到輸出信號[23]。單個神經元如圖4所示，X1至Xn 為該神經元的輸入分量，Wi1至 Win 為各輸入的權重，ui 為該神經元的組合輸入，即：ui =∑j（n）=1xj wij ，組合輸入ui 與閾值bi 計算后得到輸出 vi ，即：vi = ui + bi ，將 vi 通過激活函數f（·）進行處理可得到最終的神經元輸出 Yi。

BP 神經網絡反向傳播分為：工作信號的正向傳遞和誤差信號的反向傳遞。其中誤差的反向傳遞是 BP 神經網絡的核心[24]，主要原理是采用梯度下降法即沿著實際輸出與期望結果之差的平方和減小最快的方向，經多次迭代對網絡的權值和閾值進行優化，直至實際值與理想值的誤差最小或達到最大迭代次數時，訓練結束后，輸出模型參數，得到最終的神經網絡模型。

2.2 BP 網絡結構的設計

良好的神經網絡結構保證了運算結果的準確性。針對本文中六自由度機械臂，根據BP神經網絡的基本結構特點，設計了6輸入、6輸出的三層神經網絡結構如圖5所示，三層區域分別為輸入層、隱藏層、輸出層，6個輸入節點分別對應機械臂末端姿態參數γ、β、α和位置參數 px、py、pz ，輸出層的6個輸出節點分別對應機械臂6個關節變量即θ1、θ2、θ3、θ4、θ5、θ6。

根據公式（4）確定合適的隱藏層節個數的取值范圍，其中，h表示隱含層節點數，m表示輸入層節點數，l表示輸出層節點數，α取1～10之間的常數。通過公式可選取3～13個隱藏層節點，根據黃金分割原理不斷縮小取值區間，直到神經網絡的輸出更加逼近真實值時，最終選取11個節點單個隱藏層的神經網絡。

2.3 基于PSO算法的BP神經網絡設計及改進

BP算法的實質是以梯度下降法求誤差函數的最小值，即通過修正權值和閾值使輸出結果的誤差在期望誤差范圍內。考慮到初始權值和閾值的選取對BP神經網絡性能影響較大和易陷入局部極小值的問題，影響神經網絡的性能和準確性[25]，可通過啟發式算法和基于數值最優化理論的訓練算法來對BP神經網絡進行優化。神經網絡的輸入向量為 xm （m=1～6），輸出向量為 yn （n=1～6），隱藏層輸入向量為 Hi 、輸出向量 Ho 。機械臂末端位姿參數輸入到輸入層，待輸入到隱藏層的數據經過加權處理，如公式（5），將隱藏層輸入向量代入 sigmoid 激活函數解得隱藏層輸出向量，如公式（6）。同樣的方法得到輸出層輸入向量yi 和輸出層輸出向量yo，如公式（7），（8）。

上述公式中 H k）表示第k代樣本數據輸入到第j個隱藏層節點所得到的隱藏層輸入向量，H ）為對應的隱藏層輸出向量，其中j=1～11，ωmj 為輸入層 m 節點與隱藏層j 節點間的連接權值，bj 表示隱藏層j節點的閾值，xm 為輸入層m節點的輸入向量。 y n（k））表示 H ）輸入到輸出層n節點所得到輸出層輸入向量，y 為輸出層n節點的輸出向量，其中 n=1～6，ωjn 為隱藏層j 節點與輸出層n節點之間連接的權值，bn 表示輸出層n節點的閾值。將輸出層的實際值與理想值做差，得到均方差損失函數Loss，如公式（9）。

公式中 d ）為第k次迭代在輸出層n節點的理想輸出值。誤差函數 Loss 分別對誤差函數 Loss的隱藏層與輸出層間的權值和輸入層與隱藏層間的權值求偏導得到公式（10）。

定義δ ）為（d k）- y ））?f'（y nk ）），δ k）為 k）?ωjn ?f'（H k）），d ）表示輸出層n節點的理想輸出值，學習率μ取0.5。通過調節δ k）、δ k）來修正各層之間連接的權值ωjn 、ωmj 和閾值 bn 、 bj ，使實際輸出更接近理想值，如公式（11）。

計算參數修正后神經網絡的實際輸出值，代入公式（9）得到神經網絡的輸出誤差，當所有誤差值在理想范圍內，運算結束，得到最終的神經網絡模型，否則繼續沿著誤差平方和減小的方向修正權值和閾值直到輸出的誤差在理想范圍內。

采用粒子群優化算法（PSO）對BP神經網絡進行對神經網絡的權值和閾值進行初始化操作，以提高BP神經網絡的全局尋優能力。系統中的隨機粒子在搜索空間中經適應度函數計算和多次迭代來尋找最優解。假設在D維空間內，設置種群規模N=50，最大迭代次數T=220。空間中的粒子根據局部最優解和全局最優解來更新自己的速度和位置，如公式（12）。

公式中：v k）（t）和 x k）（t）分別表示 t 時刻粒子j在k維上的速度和位置。ω為慣性權重，值越大表示粒子種群收斂速度越快，全局尋優能力越強，一般在0～1之間內取值。 pb 為粒子本身的歷史最優解，gb 為整個種群中粒子的歷史最優解。根據標準PSO算法的參數設置要求，保證全局搜索和局部搜索的能力相等，現令加速度常數 c1= c2=2。 rand（0， 1）表示0～1的隨機數。將實際輸出均方根誤差定義為適應度函數，如公式（13）。

2.4 織機車間抓取機械臂神經網絡逆解求解

基于筒紗抓取六自由度機械臂的結構特點，設計了六輸入、六輸出的PSO-BP三層結構的神經網絡模型。輸入變量X=[γ，β， α，px，py ，pz ]包含機械臂末端的位置和姿態，輸出向量 Y=[θ1，θ2 ，θ3， θ4 ， θ5， θ6]為機械臂各關節的角度值。對神經網絡進行離線訓練和在線運行，以提高神經網絡模型的泛化能力和性能。離線訓練是將網絡的輸入值和對應的輸出值作為數據集，輸入到PSO-BP 神經網絡中，經PSO算法對網絡權值、閾值的優化和BP算法對誤差的反向傳播以縮小實際輸出與理想值之間的偏差。在線運行階段，將機械臂末端的位姿參數輸入到神經網絡模型得到實時的機械臂逆解即各關節角度大小。

根據實際作業要求確定各關節轉角范圍，如表（2），通過 MATLAB Robotic 工具箱完成對機器人正運動學求解。在關節變量的取值范圍內隨機抽取1100組關節角度值，經公式（2）求解機器人正運動學，通過公式（3）解得機械臂末端的姿態角，得到機械臂的輸入數據集，在MATLAB 環境下對神經網絡模型進行訓練，確定關鍵參數。圖6為PSO-BP神經網絡訓練流程圖。

3 仿真與實驗分析

3.1 仿真實驗

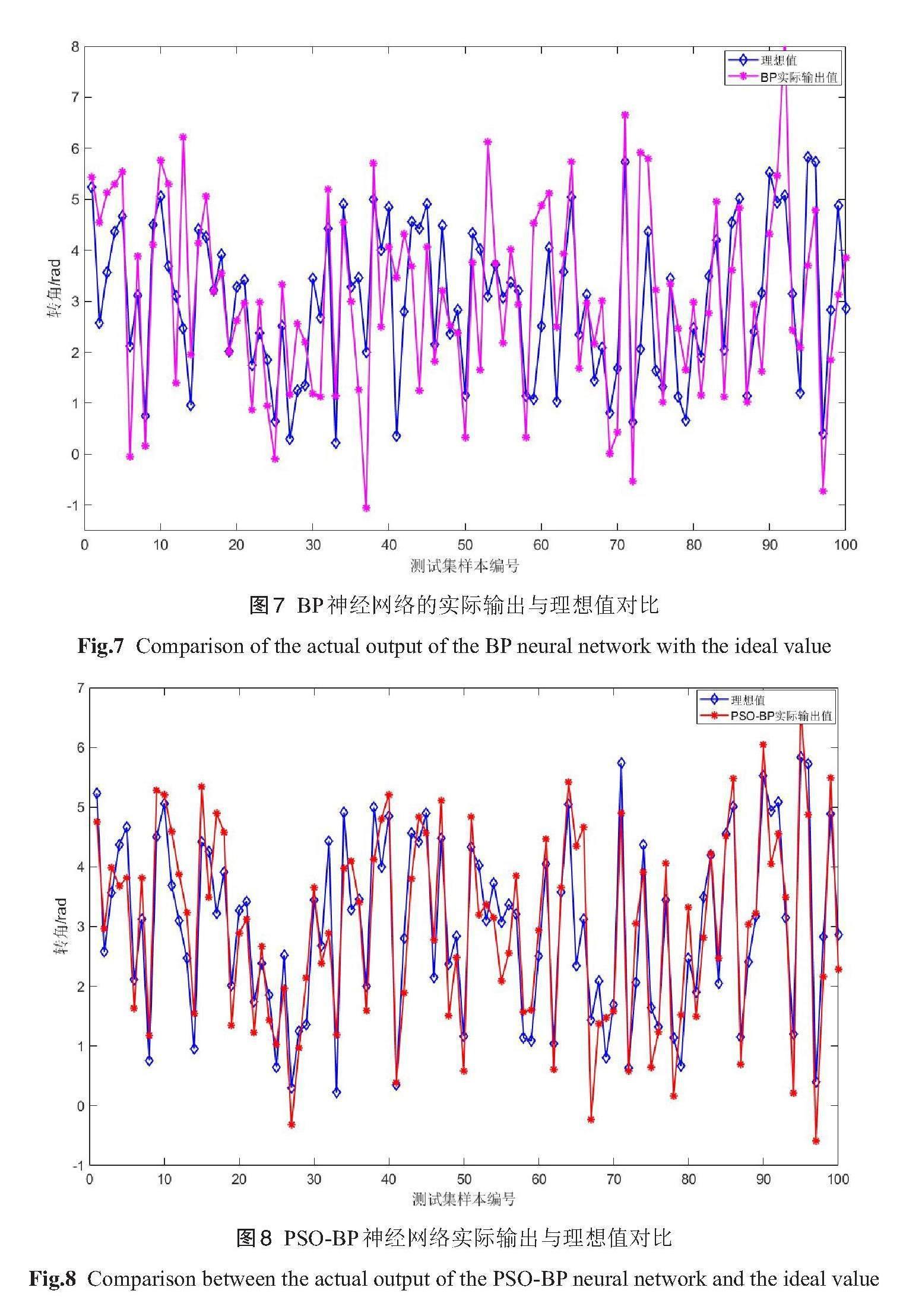
在 MATLAB 環境下根據機器人正運動學解得機械臂末端的位姿參數（γ、β、α、px、py、pz ），與各關節角度組成含有12個參數的1100組數據的數據集（γ、β、α、px、py、pz 、θ1、θ2、θ3、θ4、θ5、θ6），其中前6個參數為神經網絡的輸入量，后6個參數為輸出量。將所有數據記錄到表格中，表中每一列對應不同的參數，隨機抽取1000組為訓練集，余下的100組為測試集。測試集的位姿參數分別經過粒子群優化前后的BP神經網絡運算，分別得到對應的實際輸出值，繪制實際輸出與理想輸出的折線圖，如圖7，圖8。觀察圖像，相比于圖7，圖8中神經網絡的實際輸出與理想值的擬合程度較高。整體上看，PSO- BP神經網絡輸出值更加接近理想值，相比于傳統的BP神經網絡，經過粒子群優化的BP神經網絡具有更準確的預測能力。

提取神經網絡對關節1的預測情況，如表3所示，分析PSO算法對BP神經網絡預測性能的影響。其中BP神經網絡對關節1的最大輸出誤差為0.386，均方根誤差為0.139，PSO-BP神經網絡對關節1的最大輸出誤差為0.199，均方根誤差為0.071。經粒子群優化的 BP 神經網絡最大輸出誤差和均方根誤差都小于傳統BP神經網絡的輸出誤差。分析圖9測試集中的100個樣本誤差，可知PSO-BP的輸出的誤差波動幅度較小，且均在誤差范圍內。

分析BP神經網絡在粒子群算法優化前后的收斂性能，在相同的實驗條件及相關參數下進行對比，得到BP神經網絡和PSO-BP神經網絡迭代收斂變化趨勢，如圖10。傳統的BP神經網絡經16次迭代后適應度函數達到最小值為1.015，而PSO-BP神經網絡訓練迭代到第8次后的適應度值達到最小值為0.920。通過圖10，傳統的BP神經網絡收斂速度較慢，全局的尋優能力較弱，而經過粒子群優化的BP神經網絡在計算精度和收斂速度上都有了一定的提高，滿足筒紗抓取中對機械臂的逆運動學求解和對機械臂的實時定位控制。

4 結論

（1）提出了一種紡織車間加捻機筒紗自動抓取的智能化解決方案，通過AGV上搭載了六自由度機械臂，其末端能夠到達作業空間的任意位置，末端夾爪可對筒紗進行抓取，能夠實現對直捻機上紗管的更換任務。

（2）通過分析六自由度機械臂的結構和機械臂末端的位移參數，利用粒子群優化算法，提出了一種6輸入6輸出的PSO-BP神經網絡來對直捻機筒紗抓取機械臂求逆解。該方法能夠處理高維問題和各關節間的強耦合關系，并且 PSO- BP 神經網絡較強的泛化能力使其能夠處理復雜的、非線性的六自由度機械臂逆運動學問題。

（3）在MATLAB環境下實現了BP神經網絡對機器人逆運動學求解，通過仿真實驗對比粒子群優化算法對BP神經網絡性能的影響可知，相比于傳統BP神經網絡，PSO-BP神經網絡在機器人逆運動學求解中的精度更高、求解速度更快。

參考文獻：

[1]龔闖，戴程浩，江維，等.基于改進A*算法的大型織機車間運載機器人路徑規劃[J].紡織工程學報，2023， 1（2）：57-67.

GONG Chuang， DAI Chenghao， JIANG Wei， et al. Path planning of transport robot in large loom workshop based on improved A* algorithm[J].Journal of Advanced Textile Engineering， 2023， 1（2）：57-67.

[2]鄒亮，吳曉，袁勤政.一種自動循跡 AGV 平臺機械結構設計及力學分析[J].武漢紡織大學學報，2023， 36（5）：53-57.

ZOU Liang， WU Xiao， YUAN Qinzheng. Mechan- ical structure design and mechanical analysis of an automatic tracking AGV platform[J]. Journal of Wuhan Textile University，2023， 36（5）：53-57.

[3]陳家浩，龐愛民，李浩，等.倉儲立體庫紗錠智能配重打包方法研究[J].武漢紡織大學學報，2022， 35（5）：46-50.

CHAN Jiahao， PANG Aimin， LI Hao， et al. Re- search on the method of intelligent weighing and packing for three-dimensional warehouse[J]. Jour- nal of Wuhan Textile University， 2022， 35（5）：46-50.

[4]李進，方楚橋，王紹祥，吳曉.自動穿經機上軸車改造設計[J].紡織工程學報，2023，1（2）：90-96.

LI Jin， FANG Chuqiao， WANG Shaoxiang， WU Xiao. Reconstruction design of upper axle trolley of automatic drawing- in machine[J]. Journal of Wuhan Textile University， 2023， 1（2）：90-96.

[5]SARIYILDIZ E， CAKIRAY E， TEMELTAS H. A comparative study of three inverse kinematic methods of serial industrial robot manipulators in the screw theory framework[J]. International Jour- nal of Advanced Robotic Systems， 2011， 8（5）：9-24.

[6]李憲華， 盛蕊， 張雷剛， 等.六自由度模塊化機器人手臂奇異構型分析[J].農業機械學報， 2017， 48（7）：376-382.

LI Xianhua， SHENG Rui， ZHANG Leigang， et al. Singular configuration analysis of 6-DOF modular manipulator[J]. Transactions of the Chinese Soci- ety for Agriculture Machinery， 2017， 48（7）：376-382.

[7]姜宏超， 劉士榮， 張波濤.六自由度模塊化機械臂的逆運動學分析[J].浙江大學學報（工學版）， 2010， 44（7）：1348-1354.

JIANG Hongchao， LIU Shirong， ZHANG Botao. Inverse kinematics analysis for 6 degree-of-free- dom modular manipulator[J]. Journal of Zhejiang University（Engineering Science）， 2010， 44（7）：1348-1354.

[8]TATUM R， LUCAS D， WEAVER J， et al. Geomet- rically motivated inverse kinematics for an arm with 7 degrees of freedom[C]//IEEE.Proceeding of OCEANS 2015- MTS /IEEE.Washington： IEEE， 2015：1-6.

[9]盧喆， 鄭松.基于幾何法和旋量理論的6自由度機器人逆解算法[J].機械傳動， 2017， 41（6）：111-114.

LU Zhe， ZHENG Song. Inverse kinematics algo- rithm of 6-DOF robots based on geometric meth- od and screw theory[J]. Journal of Mechanical Transmission， 2017， 41（6）：111-114.

[10]王國勛， 舒啟林， 王軍.基于旋量理論的6R工業機器人運動學建模與分析[J].機床與液壓， 2018， 46（23）：35-42.

WANG Guoxun， SHU Qilin， WANG Jun. Kine- matics modelling and analysis for 6R industrial robot based on screw theory[J]. Hydromechatron- ics Engineering， 2018， 46（23）：35-42.

[11]林貞國.挖掘機器人軌跡規劃與仿真研究[D].太原：太原科技大學， 2017.

LIN Zhenguo， Research on trajectory planning simulation of excavator robot[D]. Taiyuan：Taiyu-an University of Science and Technology， 2017.

[12]PAUL R P， SHIMANO B， MAYER G. Differen- tial kinematics control equations for simple ma- nipulators[J]. IEEE Transactions on Systems，Man and Cybernetics， 1981， 11（6）：456-460.

[13]BIDOKHDI H S， ENFERADI J. Direct kinemat-ics solution of 3-R R R robot by using two differ- ent artificial neural networks[C]//IEEE. Proceed- ings of 20153rd RSI International Conference on Robotics and Mechatronics （IC ROM）. Teh- ran： IEEE， 2015.

[14]陳睿， 閔華松.基于BP和RBF神經網絡的機器人逆運動學算法[J].機床與液壓， 2019， 47（23）：22-27.

CHEN Rui，MIN Huasong. Inverse kinematics al- gorithm of robot based on BP and RBF neural networks[J]. Hydromechatronics Engineering， 2019， 47（23）：22-27.

[15]董慧芬， 高爽笑， 宋金海.基于徑向基神經網絡的Delta機器人位置精度補償[J].科學技術與工程， 2020， 20（31）：12883-12889.

DONG Huifen， GAO Shuangxiao， SONG Jinhai. Position accuracy compensation of delta robot Based on RBF neural network composites[J]. Sci- ence Technology and Engineering， 2020， 20（31）：12883-12889.

[16]陳平， 劉國海.基于 RBF 神經網絡的 MOTO- MAN-UPJ 型機器人運動學逆解[J].機床與液壓， 2006（12）：72-74.

CHEN Ping， LIU Guohai. A method for solving inverse kinematics of MOTOMAN-UPJ manipu- lator based on RBF network[J]. Hydromechatron- ics Engineering， 2006（12）：72-74.

[17]楊萍， 劉曉琴， 張淑珍.基于BP網絡的水輪機修復專用機器人運動學逆解分析[J].機械設計， 2005（6）：36-38.

YANG Ping， LIU Xiaoqin， ZHANG Shuzhen. In- verse kinematic solution analysis of a special ro- bot for hydraulic turbine repair based on BP net- work[J]. Mechanical Design， 2005（6）：36-38.

[18]石建平， 李培生， 劉國平， 等.基于改進克隆選擇算法的機械臂運動學逆解[J].計算機集成制造系統， 2021， 27（10）：2929-2939.

SHI Jianping， LI Peisheng， LIU Guoping， LIU Peng. Inverse kinematics of manipulator based on improved clonal selection algorithm[J]. Com- puter- Integrated Manufacturing Systems， 2021，27（10）：2929-2939.

[19]董云， 楊濤， 李文.基于解析法和遺傳算法的機械手運動學逆解[J].計算機仿真， 2012， 29（3）：239-243.

DONG Yun， YANG Tao， LI Wen. Algorithm based on analytical method and genetic algo- rithm for inverse kinematics of redundant manip- ulator[J]. Computer Simulation. 2012， 29（3）：239-243.

[20]陳睿， 閔華松.基于BP和RBF神經網絡的機器人逆運動學算法[J].機床與液壓， 2019， 47（23）：22-27.

CHEN Rui， MIN Huasong. Inverse kinematics al- gorithm of robot based on BP and RBF neural networks[J]. Hydromechatronics Engineering， 2019， 47（23）：22-27.

[21]BEHNAMIAN J， GHOMI S M T F. Develop- ment of a PSO- SA hybrid metaheuristic for a new comprehensive regression model to time-se- ries forecasting[J]. Expert Systems with Applica- tions， 2010， 37（2）：974-984.

[22]EBERHART R C， SHI Y. Comparing inertia weights and constriction factors in conference particle swarm optimiation[C]//IEEE. Congresson Evolutionary Computation. Piscataway， IEEE， 2000：84-88.

[23]BIDOKHTI H S， ENFERADI J. Direct kinemat- ics solution of 3-R R R robot by using two differ- ent artificial neural networks[C]//IEEE. Proceed- ings of 20153rd RSI International Conference on Robotics and Mechatronics （IC ROM）. Teh- ran： IEEE， 2015.

[24]芮宏斌， 曹偉， 孫寧寧.基于BP神經網絡的光伏陣列清潔機械臂逆運動學分析與時間最短運動規劃[J].太陽能學報， 2022， 43（10）：43-51.

RUI Hongbin， CAO Wei， SUN Ningning. In- verse kinematics analysis and tine opimal motion planning of photovoltaic array cleaning manipu- latory based on BP neural neteork[J]. Acta Ener- giae Solaris Sinica， 2022， 43（10）：43-51.

[25]周帥， 劉曉鳴.基于神經網絡的工業機器人力控制研究[J].機床與液壓， 2023， 51（17）：21-25.

ZHOU Shuai， LIU Xiaoming. Research on force control of industrial robot based on neural net- work[J]. Hydromechatronics Engineering， 2023， 51（17）：21-25.

（責任編輯：孫婷）