二次函數綜合題的解法探究與啟示

相晨晨

摘 要：二次函數綜合題一直是各地中考的熱點，也是教學的難點.文章以南充市2023年中考數學試題中的一道二次函數壓軸題為例，通過探求多種解法，立足核心素養，明晰思維路徑，培養學生利用數學知識解決問題的能力及提高學生的思維能力.

關鍵詞：二次函數；綜合題；解法探究；啟示

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2024）08-0002-04

二次函數是初中數學的重要內容，也是中考數學的重要考點.由于其涉及的知識面廣，思維難度大，通常以中考壓軸題的形式呈現，對學生而言具有一定的難度.解決這類問題需要學生具備較高的數學素養和思維能力.2023年南充市中考數學第25題是一道以二次函數為背景的壓軸題，具有一定的選拔功能.本文立足核心素養，明晰思維路徑，探究多種解法，培養學生利用數學知識分析問題和解決問題的能力，提升學生的數學核心素養.

1 試題呈現

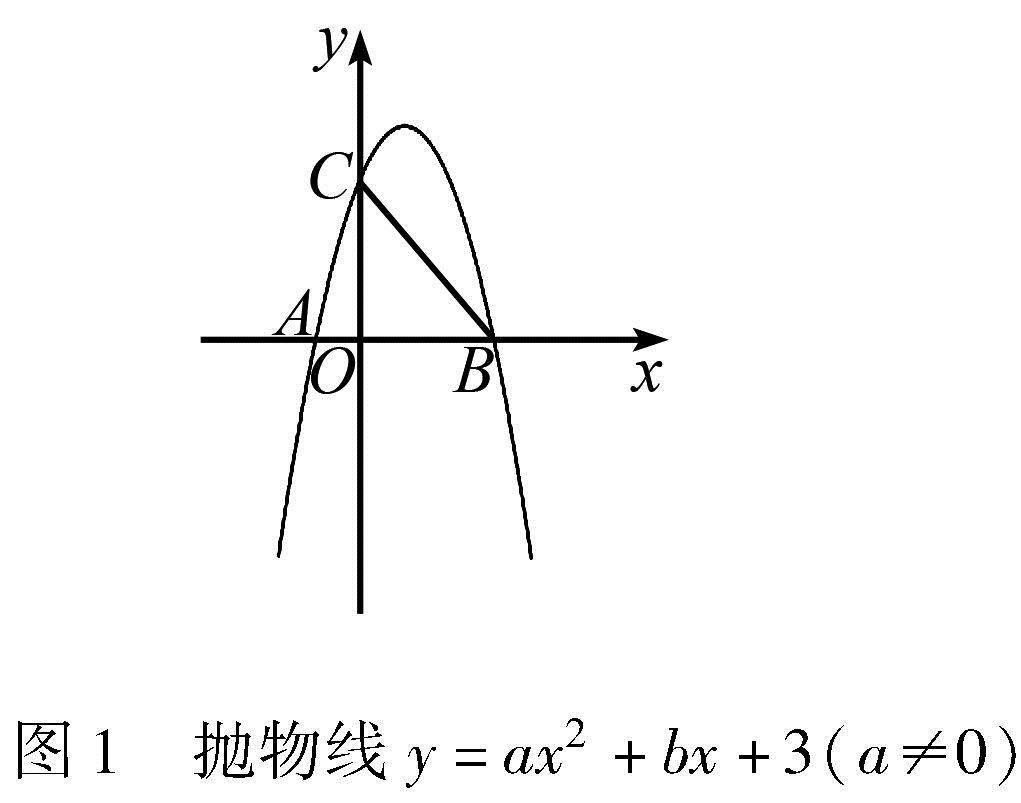
如圖1，拋物線y=ax2+bx+3（a≠0）與x軸交于A（-1，0），B（3，0）兩點，與y軸交于點C.

（1）求拋物線的解析式.

（2）點P在拋物線上，點Q在x軸上，以B，C，P，Q為頂點的四邊形為平行四邊形，求點P的坐標.

（3）如圖2，拋物線的頂點D，對稱軸與x軸交于點E，過點K（1，3）的直線（直線KD除外）與拋物線交于G，H兩點，直線DG，DH分別交x軸于點M，N，試探究EM·EN是否為定值，若是，求出該定值；若不是，說明理由.

2 試題分析

不論是從知識的綜合性還是思維的層次性來看，二次函數都當之無愧地占據著初中數學代數領域的“制高點”，是中考壓軸題的命題熱點[1].本題是一道二次函數的綜合題，以二次函數為背景并結合圖形與幾何進行命題，不僅能考查學生對二次函數和圖形與幾何相關知識的掌握情況，還能考查學生綜合應用知識的能力及靈活處理問題的心態.問題的難度層層遞進，符合學生的心理特征及由易到難的解題模式.本題以核心素養為導向，集中體現了數學課程的育人價值，符合《義務教育數學課程標準（2022年版）》所提出的命題原則，即實現對核心素養導向的義務教育數學課程學業質量的全面考查[2].

本題主要考查的核心概念有二次函數、平行四邊形的性質、一次函數、線段定值等，蘊含豐富的數學思想和方法，主要有方程思想、函數思想、數形結合思想、分類討論思想和模型思想等.綜合考查了學生的運算能力、幾何直觀、空間觀念、推理能力和創新意識等核心素養.

問題（1）難度較小，考查二次函數的解析式，學生只要熟知二次函數相關知識及求解方法，就能很容易解出正確答案.此問題主要考查學生的運算能力，培養學生會用數學的眼光觀察現實世界.問題（2）難度上升，從學生的認知規律來看，只要學生認真審清題目，提取有關信息，采用“爬山法”，一步一步分析題目，也能很快解決問題.而本題是從平行四邊形的性質出發，最終落腳到點的坐標，解題最關鍵的一點是學生能夠考慮到分類討論的思想，想到固定點B，C組成的線段，而點P在拋物線上，通過拋物線的圖象來看，點P有可能在x軸的上方，也有可能在x軸的下方，然后采用數形結合的方法解決問題.此問題主要考查學生的運算能力、幾何直觀、推理能力等，培養學生會用數學的眼光觀察現實世界和用數學的思維思考現實世界.問題（3）難度要比前兩個問題高，學生要根據題目的信息先提出猜想，再進行證明，最后得出結論，并借助尺規將數學語言轉化為實際圖形，促進學生理解和思維的轉變.此問題需要學生解出三個一次函數的解析式，并通過方程思想，解出兩根之間的關系，再通過射影定理模型得出結論，對學生運算能力和邏輯思維能力的要求相對較高，知識的綜合性更強，這不僅考查學生的“四基”和“四能”，更考查學生是否具有穩定的心態，培養學生會用數學的語言表達現實世界.

3 試題解答

3.1 問題（1）的解法

解法1 （代入法）將A（-1，0），B（3，0）兩點

解法2 （對稱法）因為拋物線y=ax2+bx+3（a≠0）與x軸交于A（-1，0），B（3，0）兩點，從而得出拋物線y=ax2+bx+3（a≠0）的對稱軸為x=1，所以b=2a.將A（-1，0）代入拋物線中a-b+3=0，從而得出a=-1，b=2，所以拋物線的解析式為y=-x2+2x+3.

解法3 （兩點式）根據題意，可設拋物線的解析式為y=a（x+1）（x-3）=ax2-2ax-3a，從而得出-3a=3，解得a=-1，進而得出拋物線的解析式為y=-x2+2x+3（a≠0）.

3.2 問題（2）的解法

根據已知條件，以B，C，P，Q為頂點的四邊形為平行四邊形，但并沒有明確說明P的位置，所以要對點P的位置進行分類討論，分為兩種情況，第一種是P在x軸的上方，第二種是P在x軸的下方.

第一種情況：P在x軸的上方.

解法1 （平行四邊形的性質）如圖3，過點C作CP∥BQ，過點P作PN⊥OQ，設點P的坐標為（t，-t2+2t+3），因為四邊形BCPQ為平行四邊形，所以BC=PQ，CP=BQ進而得出Q（t，0），OQ=3+t，ON=t，NQ=3，所以PQ2=PN2+NQ2，即（-t2+2t+3）2+9=18，當-t2+2t+3=3，解得t=0（舍去）或t=2;當-t2+2t+3=-3，因為P在x軸的上方，所以-t2+2t+3=-3舍去，從而只有t=2符合題意，進而求出點P的坐標為（2，3）.

解法2 直線CB的斜率為kCB=-1，又因為CB∥PQ，所以kPQ=-1，-t2+2t+3=3，解得t=0（舍去）或t=2，只有t=2是符合題意，從而求出點P的坐標為（2，3）.

第二種情況：P在x軸的下方.

評析分類討論是二次函數綜合題常用的方法之一，是學生在學習過程中必須掌握的解題思想.解決本題的關鍵是對點P的位置進行分類討論，從已知條件出發，可以把點P分為在x軸的上方和在x軸的下方.

3.3 問題（3）的解法

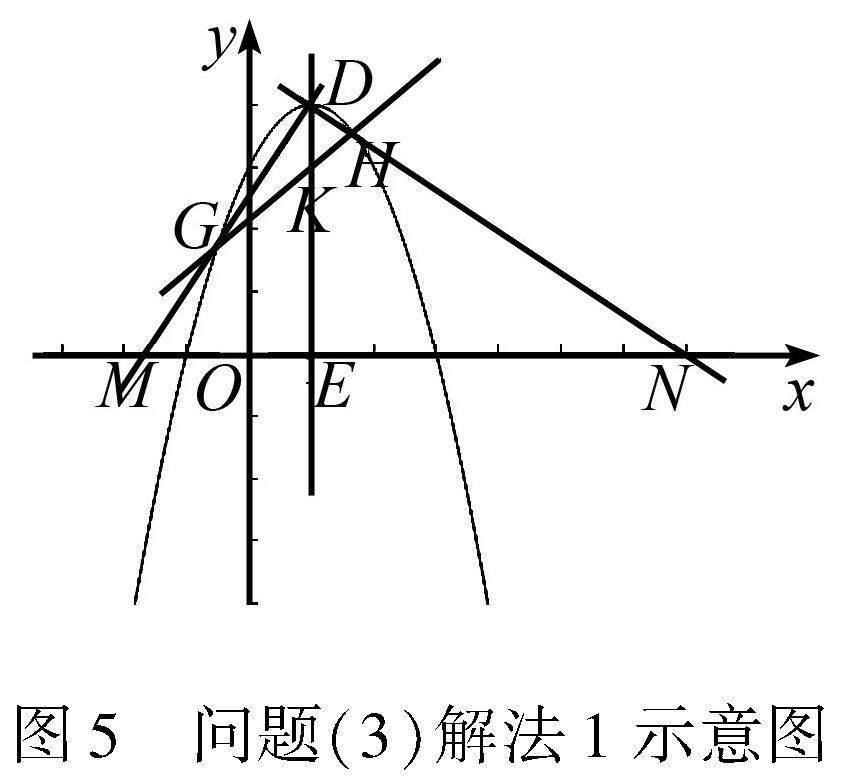
評析這類解法思路很明確，求出點的坐標，然后根據點的坐標求相關線段的長度，進而計算EM·MN的值.雖然運算量較大，需要明確三條直線的解析式，但是解題的思路比較清晰.

評析 根據點的坐標，利用兩點間的距離公式可求得相關線段的長度，然后利用勾股定理的逆定理即可判定△MDN是直角三角形，最終利用直角三角形和相似三角形的性質解決問題.

解法3 如圖6所示，設過點D的直線解析式為y=kx+b，將D（1，4）代入直線解析式，得出y=kx+3-k，因為G，H在拋物線上，可設G（x1，kx1+3-k），H（x2，kx2+3-k），從上面可知x1+x2=2-k，x1x2=-k，過點G作GF

評析 根據圖形特征，一條線段上有垂直線，并求EM·EN，要能夠想到射影定理，利用三角形相似，證明兩個三角形相似要從角或者線段成比例角度考慮，同時解題的關鍵是要證明出∠MDN=90°.

解法4 在上面的解法中已經求出了直線DG解析式為y=-（x1-1）x+x1+3，同理可求出直線DN的解析式為y=-（x2-1）x+x2+3，從而可以得出kDG=-（x1-1），kDN=-（x2-1），又因為x1+x2=2-k，x1x2=-k，所以kDG·kDN=（x1-1）×（x2-1）=-1，則直線DG與直線DN互相垂直，進而∠MDN=90°，所以∠MDE+∠EDN=90°，所以∠MDE=∠DNE，所以△EMD△EDN，從而得出ED2=EM·EN=16.因此，EM·EN是定值.

評析 通過對圖形的觀察，發現解題的關鍵是要證明∠MDN=90°，兩直線的夾角為直角，說明兩直線互相垂直，則可以通過斜率關系進行證明，最后能求出EM·EN的值.

4 解題反思

4.1 重視變式訓練，發展思維能力

題目不在于多，而在于精.一道題目不僅是一個知識點，它還可以是多個知識點的結合.在教學中教師可以圍繞著一個問題向多個方向發散，把一道題變成一類題.就如本題中的二次函數，在方法上，對于點P的位置進行分類討論，通過變式的形式可以從B，C所組成的線段是邊還是對角線進行分類討論，打破學生的常規思維.在內容上，除了可以考查線段乘積的定值和點的存在性，還可以與中點問題、線段的最值問題、面積定值、一次函數特殊角等問題進行結合.基于此，在教學中要不僅要培養學生能夠靈活選擇數學方法解決問題的習慣，還要通過“一題多解”培養學生思考問題和靈活變通的意識，而“一題多解”不僅有利于學生發散思維的培養，更有利于學生問題解決策略的形成、關鍵問題解決能力的培養[3].所以，在教學中教師可以通過變式進行教學，發展學生的思維能力，培養學生的發散思維，打破學生的思維定式，培養學生創新意識和實踐能力.

4.2 構建知識網絡，提高運算能力

綜合題往往不是一個數學知識點，而是多個數學知識的結合，所以在復習的過程中，要提高學生搭建知識網絡的能力，形成知識框架，在教學中可以通過主題式學習，將知識進行整合.知識是解決問題的前提，而解決問題的成敗關鍵在于學生的運算能力，它不僅是一種數學的操作能力，更是一種數學的思維能力[4]，教師在教學中可以通過日常的運算訓練來發展學生的運算能力，有利于培養學生的思考問題的品質和養成科學的學習態度.

參考文獻：

［1］ 石樹偉.中考二次函數模型試題的源與流[J].中學數學月刊，2022（5）：60-63.

[2] 中華人民共和國教育部.義務教育數學課程標準（2022年版） [M].北京：北京師范大學出版社，2022.

[3] 高巖.二次函數背景下三角形面積最值問題的解法探究：由一道九年級期末壓軸題引發的思考[J].初中數學教與學，2022（9）：20-22.

[4]金小亞.借助幾何直觀 培養運算能力[J].教育實踐與研究（A），2019（1）：25-28.