基于混合裁剪失衡數據增強與SwinNet網絡的滾動軸承故障診斷

火久元, 李宇峰, 常 琛, 李超杰, 許繼豪

(1. 蘭州交通大學 電子與信息工程學院,蘭州 730070;2. 蘭州瑞智元信息技術有限責任公司,蘭州 730070)

目前,故障診斷技術已逐漸成為提升機械系統可靠性和安全性的關鍵手段[1]。優秀的故障診斷方法可以準確判斷故障發生的位置,辨識發生故障的類型,避免造成嚴重的經濟損失和人身傷害[2]。滾動軸承作為旋轉機械系統關鍵部件之一,在各個行業中都有非常廣泛的應用[3],是影響機械設備能否安全運行的重要因素[4]。因此,開展滾動軸承故障診斷研究對提高機械設備運行效率,實現機械設備健康管理具有重要意義。

對滾動軸承進行故障診斷的方法通常分為4類,分別是基于模型的、基于經驗的、基于傳統機器學習的與基于深度學習的[5]。但是由于現代工業設備比較復雜并且缺乏足量的先驗知識,因此通過基于模型的或者基于經驗的故障診斷方法存在一些限制條件[6]。傳統的機器學習方法已經被廣泛的應用于故障診斷領域。Van 等[7]使用經驗模態分解對信號進行分解,然后利用支持向量機算法來對軸承故障進行分類,取得了顯著的分類效果,但其需要手動進行特征提取與特征選擇,存在一定的局限性。He等[8]提出了一種利用多尺度隨機共振譜圖來對軸承進行故障制度的方法,但是此方法在處理大量振動信號時計算難度大,且過度依賴于研究人員的專業知識。

近年來,深度學習方法由于其具有自適應地從監測數據中進行故障特征學習的優勢,得到越來越廣泛的關注。如吳春志等[9]設計出了一種一維卷積神經網絡,以原始振動信號作為模型輸入完成了對齒輪箱的故障診斷。張立智等[10]提出了一種利用短時傅里葉變換結合卷積神經網絡模型進行故障診斷的方法,該模型具有強大的特征提取能力。Han等[11]提出了一種將卷積神經網絡的特征處理能力與支持向量機的泛化能力相結合的方法,解決了小樣本數據集難以訓練復雜模型的問題。此外,一些學者在故障診斷模型中引入了注意力機制來增強卷積神經網絡處理長距離依賴關系等方面的能力。Li等[12]引入了一種注意力機制來輔助單位信息數據段,提取輸入的判別特征來完成滾動軸承的故障診斷。Ding等[13]構建了一種擁有全新的注意力機制的TransFormer結構,實現了滾動軸承端到端的故障診斷。

在理想的環境中,各種故障診斷方法都能夠取得出色的效果,尤其是在大量故障樣本和健康樣本進行訓練的情況下對滾動軸承進行故障診斷。這樣的訓練數據確保了算法具備足夠的準確性。如果在沒有環境噪聲和人為噪聲干擾的情況下,這些方法甚至可以實現接近100%的故障診斷精度。然而,機械設備通常處于正常服役狀態,其故障樣本數量往往遠少于正常樣本數量[14]。此外,大多數滾動軸承密閉于機械系統內部,受到電磁干擾的影響會讓采集到的振動信號中不可避免地包含噪聲[15]。同時,在對故障數據進行標記時可能會出現人為的操作失誤而導致真實標簽與標記標簽不符的情況發生[16]。這些情況的出現都會大幅度降低故障診斷模型的診斷精度。因此,本文提出了一種基于混合裁剪失衡數據增強與SwinNet網絡相結合的故障診斷模型,利用混合裁剪失衡數據增強算法來解決故障類別失衡問題,同時有效地結合SwinNet網絡,完成在有噪聲干擾與在有噪聲標簽干擾時對滾動軸承的故障診斷。

1 理論基礎

1.1 小波變換

相較于一維信號,二維圖像是更強大的信息表達方式。小波變換是一種信號處理技術,它能夠將信號分解為不同尺度和頻率成分。在低頻段,小波變換能夠提供更高的頻率分辨率和更低的時間分辨率,在高頻段,小波變換能夠提供更高的時間分辨率和更低的頻率分辨率,這與信號變換的特性相符[17]。因此,本文使用小波變換來將滾動軸承振動信號轉換為二維時頻圖像,從而能夠同時顯示全局的低頻信息和局部的高頻特征,更好地揭示故障信號的本質特征[18]。小波變換操作如式(1)所示

(1)

式中:a為尺度參數,a>0;b為時間平移量;P(b)為原始的故障信號;φ為母小波;Wp(a,b)為連續小波變換。

1.2 卷積神經網絡

卷積神經網絡(convolutional neural networks, CNN)是一種常見的深度學習神經網絡模型,常用于圖像和視頻等數據的分類和處理。CNN的基本結構大多由卷積層、池化層和全連接層組成。

卷積層是CNN中最重要的層級之一,它的主要目的是從輸入數據中提取特征[19]。一般的卷積計算如式(2)所示

Mi+1=[Mi?Wi]+d

(2)

式中:Mi+1為第i層的特征輸出圖;Mi為第i層的特征張量;Wi為第i層感受器的權值向量;d為第i層的偏置向量; ?為卷積計算。

池化層是一種常用的降采樣技術,用于減少卷積層輸出的特征圖的大小[20]。主要池化操作有最大池化和平均池化,如式(3)、式(4)所示

(3)

(4)

式中:uP(i,t)為第p層中第i個特征張量的第t個神經元;w為卷積核寬度;j為第j個池化層。

全連接層是將前面的卷積層和池化層的輸出連接成一個全連接的神經網絡層,用于對輸入特征進行分類或者回歸。如式(5)所示

q(x)=f(wx+c)

(5)

式中:x為全連接層的輸入;w為權重;c為偏置;f為激活函數。

1.3 Transformer

隨著Transformer模型在自然語言處理領域的成功應用,研究人員開始將其引入到了圖像處理領域。最早的工作是將Transformer應用于圖像分類任務中,這些模型通常被稱為ViT(vision transformer)[21]。ViT將圖像的像素數據視為一維序列,通過將像素轉換為一組向量后送入到對應模塊中進行分類。為解決ViT在處理圖像時需要大量的計算和內存資源的問題,提出了一種Swin Transformer網絡作為可行解決方案,其擁有類似于金字塔形式的架構,可以大大降低模型對于計算和內存的要求[22]。傳統的Swin Transformer塊結構如圖1所示。

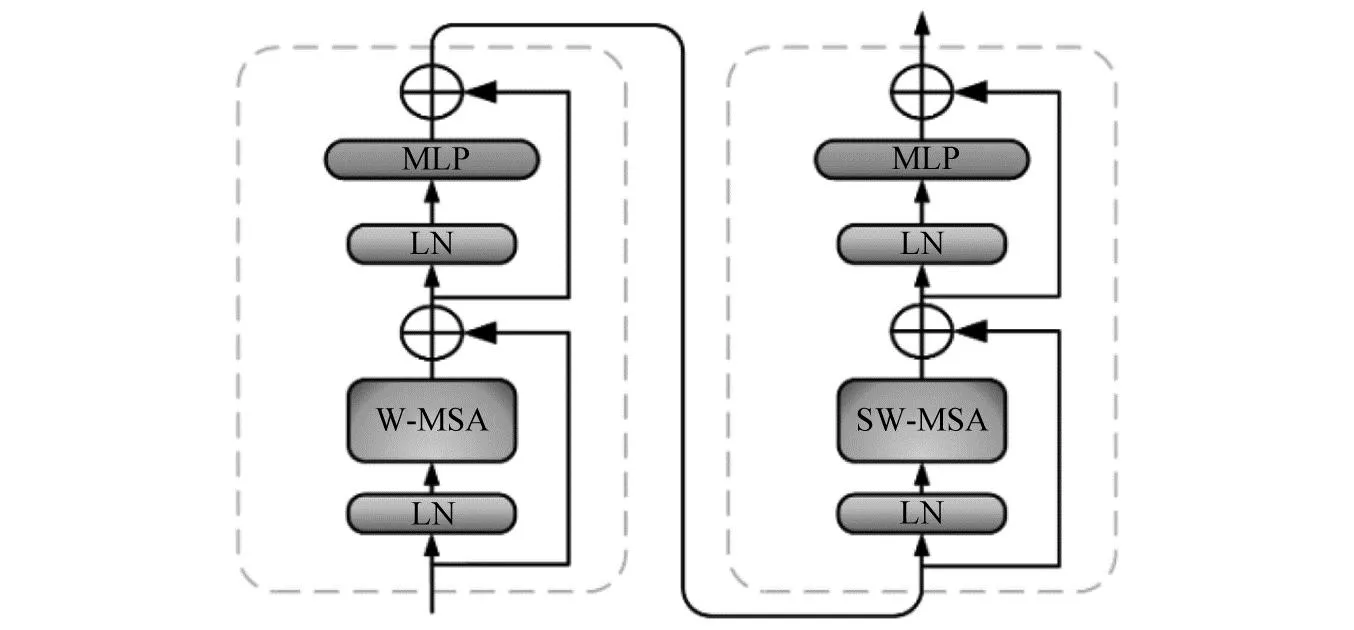
圖1 Swin Transformer塊結構Fig.1 Swin Transformer block structure

圖1中,Swin Transformer采用了一種窗口化的自注意力機制,將輸入的特征圖分割成多個大小相同的窗口,每個窗口內部進行多頭注意力機制的計算。通過這種方式,模型可以僅對每個窗口內的信息進行關注和計算,避免了對整個圖像的計算。此外,為了使信息在窗口之間進行傳遞,Swin Transformer還采用了一種移動窗口的自注意力運算機制,該機制可以將注意力權重向左或向右偏移一定距離,以實現窗口間的信息交流。

2 基于混合裁剪失衡數據增強與SwinNet網絡的故障診斷模型

2.1 混合裁剪失衡數據增強算法

在實際工況下,正常樣本數量通常遠遠多于故障樣本數量,這往往會導致故障診斷模型診斷能力降低以及泛化能力不夠等問題。受到Bai等[23]提出的數據增強算法啟發,通過借鑒圖像裁剪的數據增強思想,本文提出了一種混合裁剪失衡數據增強(mixed-cutout imbalanced data augmentation,MCIDA)算法,如式(6)所示

(6)

式中:S為通過一次MCIDA算法進行擴充后的樣本數;M為數據集原始時間序列長度;N為數據樣本長度;K為需要對原始數據集進行擴充的倍數;i的取值為1～K的整數。

當數據失衡的情況發生時,為生成足夠多的數據來作為故障診斷模型的輸入,對于失衡的故障數據類別通過MCIDA算法進行樣本擴充,保證擴充后的故障類別樣本數盡量與滾動軸承健康狀況下的樣本數相同。以對失衡的故障類別進行5倍混合裁剪失衡數據增強為例,其原理如圖2所示,對應的算法原理偽代碼如表1所示。

表1 算法原理偽代碼Tab.1 Pseudocode for algorithm principle

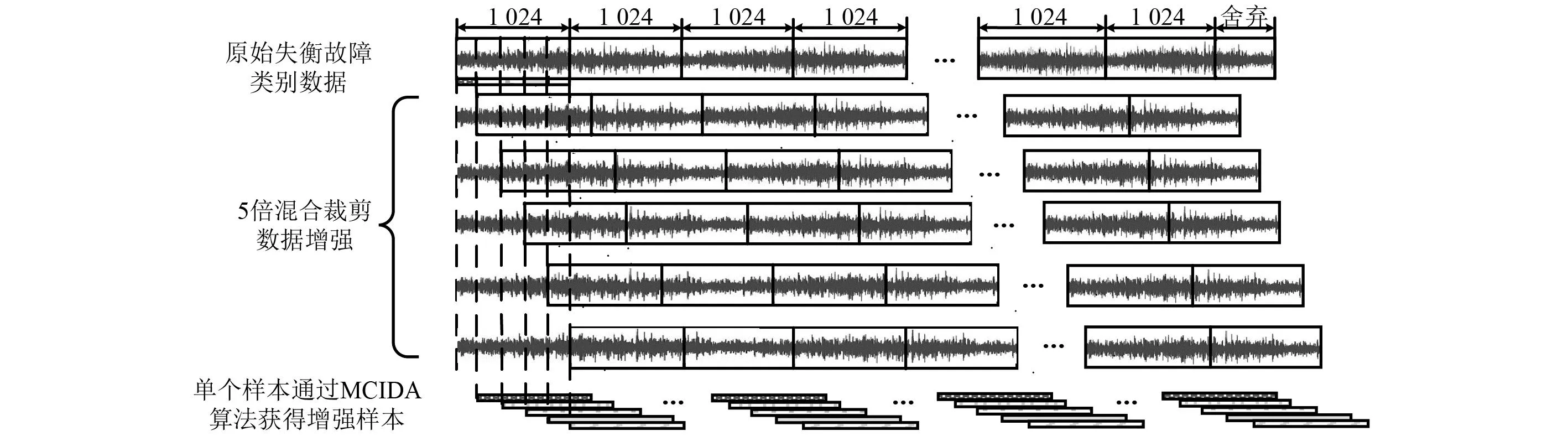
圖2 5倍混合裁剪失衡數據增強Fig.2 5 times mixed cropping imbalanced data augmentation

結合圖2與見表1,原始數據集的失衡類別樣本按照該算法最終可以獲得5組樣本集,將這5組樣本集進行混合就可以獲得最后的增強數據集。

通過MCIDA算法進行重新劃分獲得的樣本集中的各個樣本一定不會發生重復,并且增強數據集中的任何一個樣本也不會與原始數據集失衡類別中的樣本相同。

2.2 SwinNet網絡

滾動軸承的故障特征受到振動耦合的影響往往會表現出多尺度性質[24]。基于傳統CNN的故障特征提取方法已無法適用于較為復雜的滾動軸承故障診斷場景中,為提高故障診斷模型的性能,需要獲取更加全面的故障特征,因此,本文將CNN與Swin Transformer編碼器相結合設計出了以時頻圖像作為輸入的SwinNet網絡模型。該SwinNet網絡結構如圖3所示。

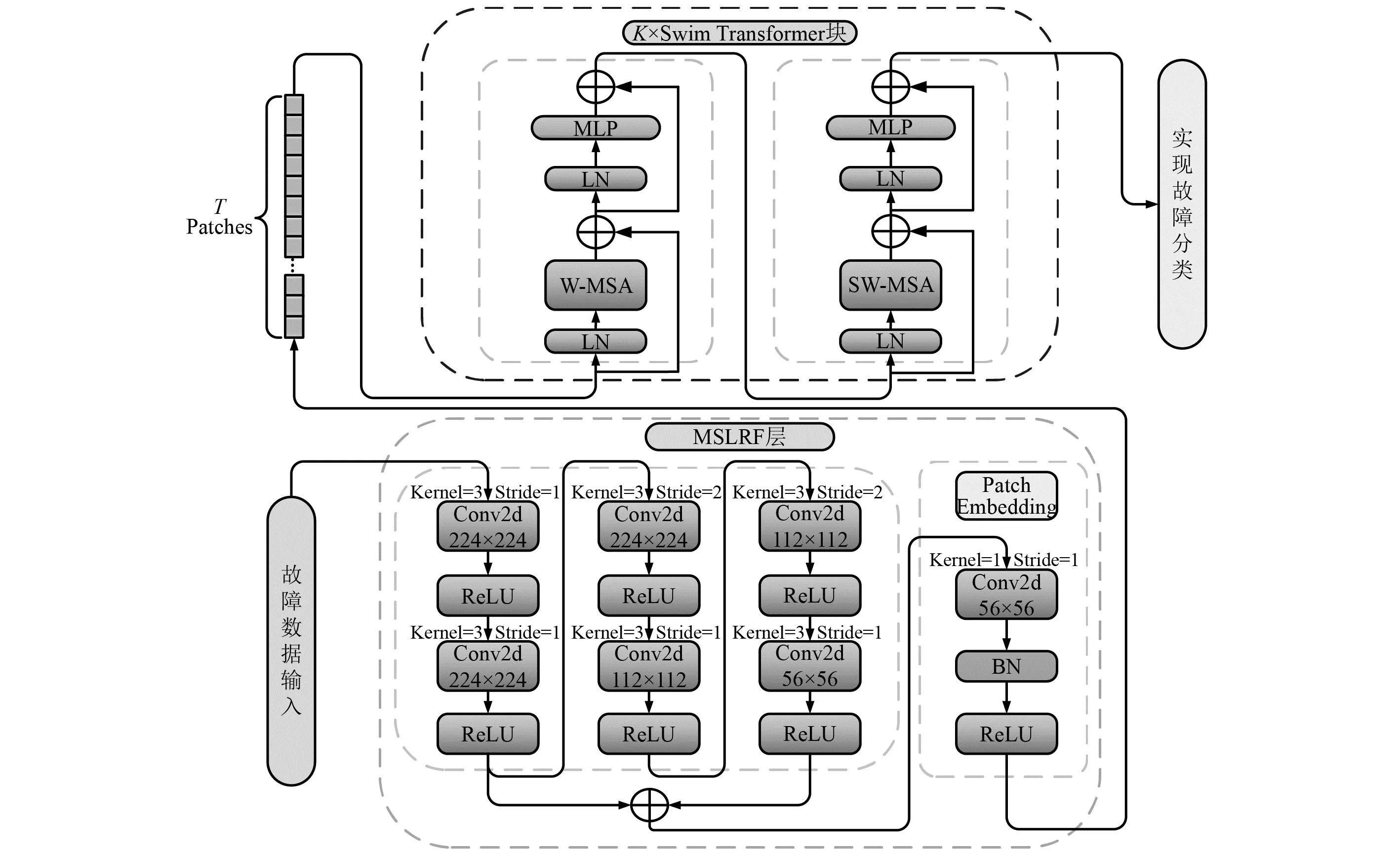
圖3 SwinNet網絡模型結構Fig.3 SwinNet network model architecture

該網絡包含了一個多尺度局部感受野特征提取(multi-scale local receptive field feature extraction,MSLRF)層和多個Swin Transformer編碼器。首先,借助卷積核的帶通濾波特性,利用MSLRF 層中的卷積模塊提取圖像的低維特征,保證每個卷積層可以捕獲不同尺度和方向的局部信息。然后,利用MSLRF層中的Patch Embedding能力將每一張圖片分解為多個小塊,從而更好地表示圖像中的局部信息。最后,將提取到的每個小塊中的局部窗口特征傳遞到Swin Transformer編碼器中實現跨窗口交互捕捉全局信息,從而進一步提高特征提取能力。總之,SwinNet網絡可以將CNN的歸納偏置能力與Swin Transformer編碼器的移動窗口多頭注意力機制進行結合從而完成滾動軸承故障的高效診斷。

2.3 故障診斷流程

基于MCIDA-SwinNet方法的故障診斷整體流程如圖4所示。具體過程如下:

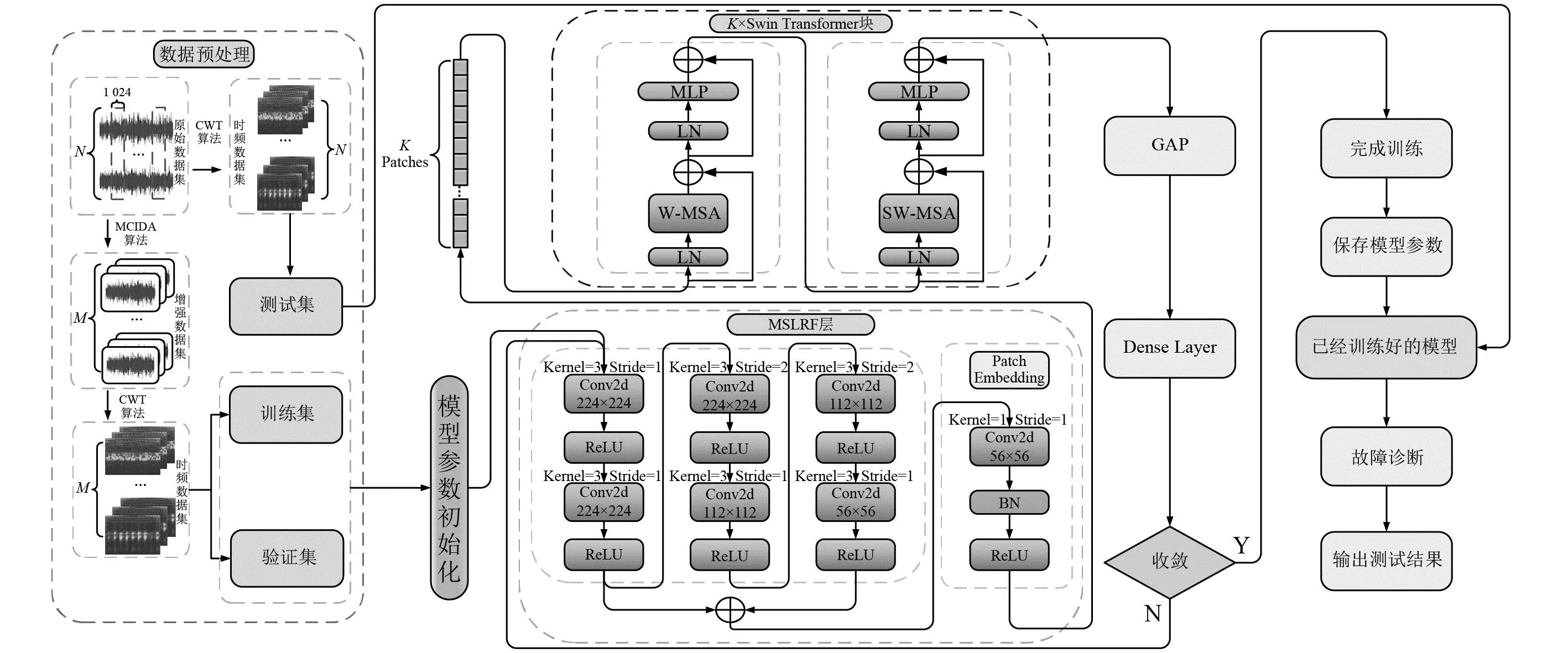
圖4 基于MCIDA-SwinNet方法的故障診斷流程Fig.4 Thefault diagnosis process based on MCIDA-SwinNet method

(1) 對原始的振動信號數據進行樣本的劃分,將需要進行數據增強的失衡數據集按照MCIDA算法進行數據增強。通過小波變換算法對增強數據集與原始數據集進行時頻圖像的轉換,并且將增強數據集按照比例劃分為訓練集與驗證集,原始數據集作為測試集。

(2) 對SwinNet網絡的參數進行初始化,設置SwinNet網絡的drop_rate參數為0.1,droppath參數為0.2,使模型在訓練過程中隨機丟棄網絡中的某些連接,減少不同層之間的耦合和復雜性,從而增加模型的魯棒性和泛化能力,防止過擬合的產生。此外,設置SGD(stochastic gradient descent)優化算法來更新網絡超參數,將學習率初始化為0.001,根據驗證集的損失函數值動態更新學習率,并且設置權重衰減參數進一步減小過擬合的風險。

(3) 網絡進行訓練,首先,輸入數據經過MSLRF層和多個Swin Transformer塊得到表示圖像信息的特征向量。然后,特征向量輸入到全局池化層中得到完整的圖像語義表示。最后,通過全連接層進行故障分類。當驗證集的損失函數值不再下降時,保存收斂后的模型。將測試集輸入到訓練好的模型之中,最終得到故障診斷分類結果,完成故障診斷流程。

3 試驗驗證與分析

為驗證所提出的故障診斷方法的診斷性能,本文使用美國凱斯西儲大學(Case Western Reserve University,CWRU)電擊軸承采集的公開數據集進行試驗。采用的深度學習框架為Pytorch,在Windows Server 2016上利用python語言進行編程。計算機的配置為:Inter(R) Xeon(R) Silver 4210R CPU @ 2.40 GHz 2.39 GHz,NVIDIA Tesla T4顯卡,64 GB內存。為客觀反映試驗的有效性并且排除偶然性,每組試驗都重復多次,然后取平均值作為最終結果。

3.1 數據說明

本試驗進行診斷的軸承型號為SKF6205[25],該軸承存在3種故障損傷的位置,分別是軸承滾動體故障、外圈故障與內圈故障。3種故障損傷的損傷直徑大小分別為0.177 8 mm、0.355 6 mm、0.533 4 mm。每一種故障數據可以分別通過驅動端、風扇端、底座端的加速度計來收集到。本文所使用的故障數據是當電機轉速為1 772 r/min,采樣頻率為12 kHz時,從驅動端的傳感器獲得的軸承振動信號數據。按照該軸承故障位置與故障直徑進行軸承狀態類別劃分,其狀態類別可以劃分為10類。將該軸承振動信號數據以1 024個樣本點為1個樣本進行樣本劃分,得到不同狀態類別的時域波形圖像與頻域波形圖像如圖5所示。

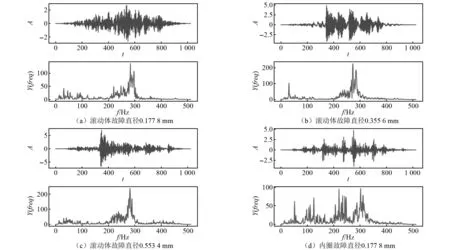
圖5 不同狀態類別的時域波形圖與頻域波形圖Fig.5 Time-domain waveform and frequency-domain waveform images of different state categories

3.2 基于MCIDA算法的數據增強試驗

本試驗依據滾動軸承不同狀態類別的失衡樣本數量的失衡比值(imbalance ratio,IR)構造了4組失衡數據集。其失衡樣本數量的比值如式(7)所示。

IR=X∶Y

(7)

式中:X為故障樣本的數量;Y為健康樣本的數量。IR分別設置為1∶20、1∶10、1∶5、1∶2,4組失衡數據集的9種故障狀態與1種健康狀態的樣本數量如表2所示。設置每組失衡數據集的健康樣本數量為200個,故障類別樣本數量分別設置為10、20、40、100個。得到劃分后的4組失衡數據集的樣本總數分別為290、380、560、1 100個。

基于MCIDA算法來構造增強數據集,對第1組失衡數據集進行增強,每一類的失衡故障樣本數將由10個擴增到180個。同樣的使用該MCIDA算法可以分別將第2、3、4組的失衡故障樣本數擴充到190、195和198個。這樣最后獲得的4組增強數據集的樣本總數分別為1 820、1 910、1 955、1 982個。自此一共得到8組數據集,即4組原始失衡數據集與4組增強數據集。

使用小波變換算法將8組數據集的振動信號數據樣本轉換為二維時頻圖像數據樣本,以此圖像數據作為SwinNet網絡的輸入數據。考慮到較小尺寸時頻圖像信號的某些部分會糾纏到一起導致無法區分,而根據奈奎斯特-香農采樣定理,適當的增加圖像尺寸可以改善這一問題[26]。綜合考慮使用尺寸為224×224的時頻圖像作為網絡模型的輸入數據。該滾動軸承10種不同狀態類別下的二維時頻圖像,如圖6所示。由圖6(a)～圖6(c)可知,不同直徑的滾動體故障呈現出周期性的、分離的特征,其周期性特征與故障直徑相關; 由圖6(d)～圖6(f)可知,不同直徑的內圈故障在特定頻率上展現出獨特的時域反射特征強度;而由圖6(g)～圖6(i)可知,不同直徑的外圈故障在不同頻率和時域上會表現出短時能量集中的特征;只有圖6(j)所展示的健康軸承狀態的二維時頻圖像呈現出了均勻且較為平滑的特征。

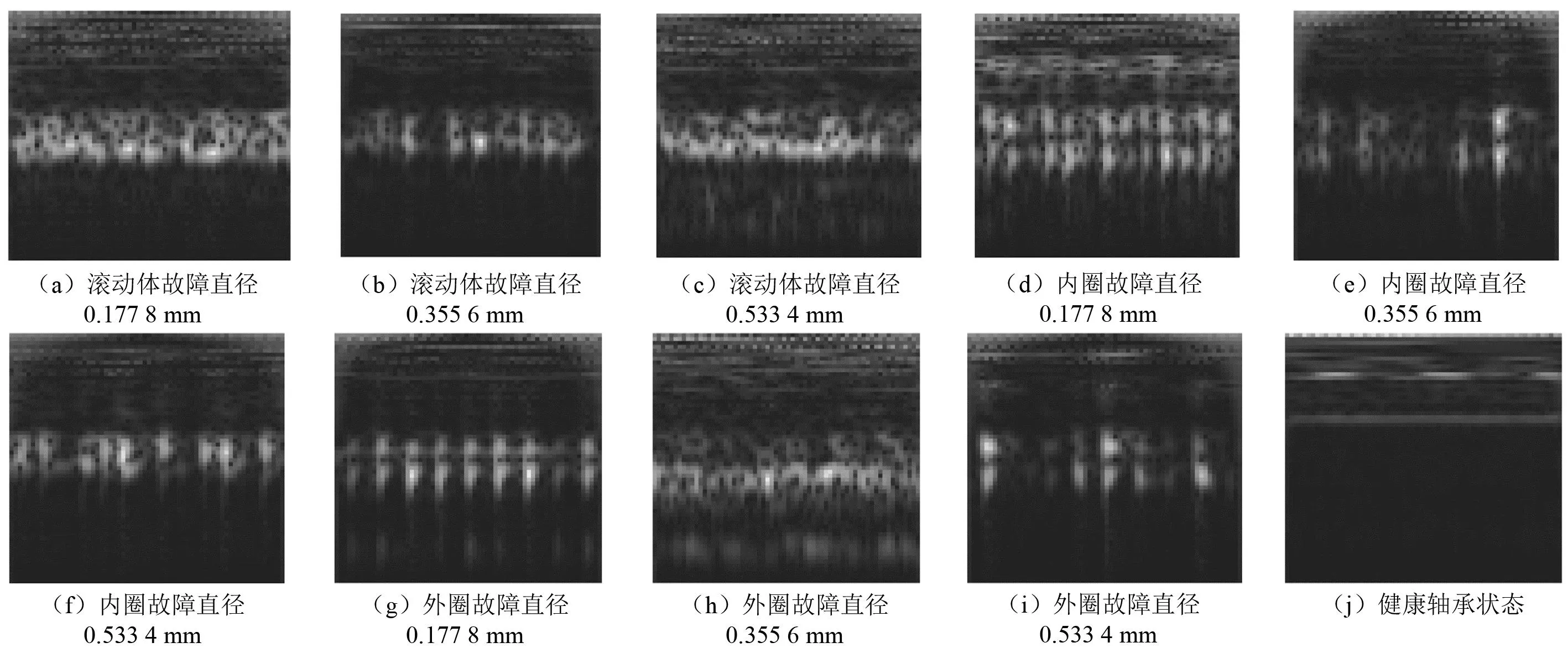
圖6 二維時頻圖像Fig.6 Two dimensional time-frequency images

使用失衡數據集按照7∶3的比例劃分出訓練集和驗證集進行SwinNet網絡訓練的訓練情況如圖7(a)所示,unba_10、unba_20、unba_40、unba_100分別代表的是使用4組失衡數據集進行訓練的曲線。由于失衡數據集故障樣本較少,正常樣本較多,這導致網絡訓練曲線波動性較大,穩定性不夠。隨著類失衡程度加劇,SwinNet網絡的特征提取能力減弱,其在IR為1∶20時的訓練精度只能達到94.12%左右。為了驗證MCIDA算法不僅能夠提高網絡訓練的穩定性,還可以提高網絡的特征提取能力,針對每一組增強數據集按照7∶3的比例劃分出訓練集和驗證集,而將原始的失衡數據集作為測試集。SwinNet網絡使用增強數據集訓練的情況如圖7(b)所示,ba_10、ba_20、ba_40、ba_100分別代表的是使用4組增強數據集進行訓練的曲線。可以發現使用增強數據集進行訓練的曲線波動非常小,具有較強的穩定性,當迭代到第50次后,所有的訓練曲線都達到收斂狀態。最后4組增強數據集的訓練集平均收斂精度都可以達到98.7%左右。

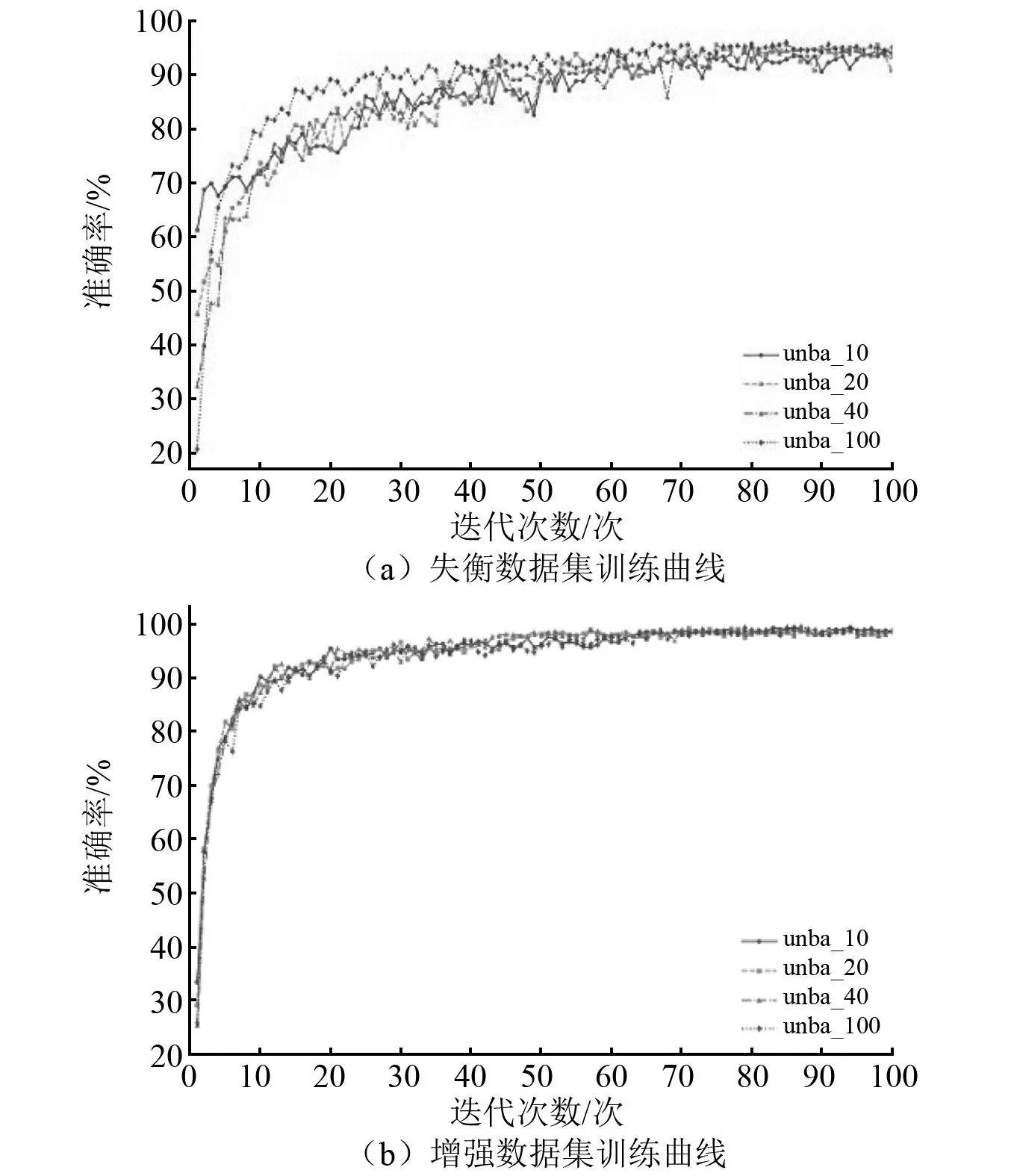
圖7 SwinNet網絡訓練曲線Fig.7 SwinNet network training curves

為了驗證MCIDA算法擁有較強的泛化能力,使用4組增強數據集來對AlexNet、ResNet、M1DCNN[27]、MTSC-CNN[28]故障診斷模型進行訓練,使用原始數據集來作為測試集。本文提出的SwinNet網絡與其他4種對比算法的測試集結果如表3所示。

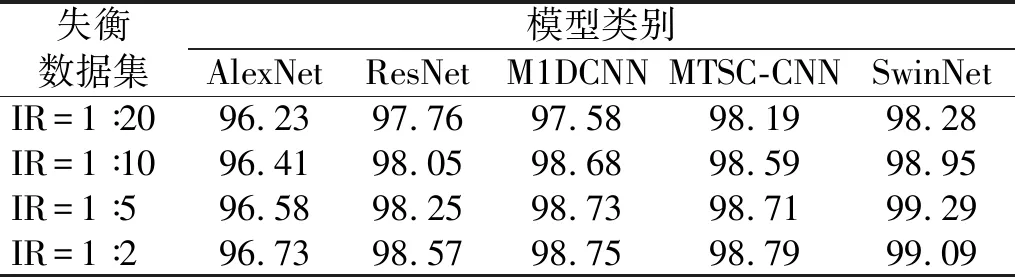
表3 不同故障診斷模型的測試集精度Tab.3 Test set accuracy of different fault diagnosis models

由表3可知所有模型使用測試集進行測試的診斷精度均能夠達到96%以上,這充分證明了MCIDA算法的普適性,大多數深度學習故障診斷模型通過該增強算法增強后的增強數據集進行訓練后都可以獲得不錯的故障診斷精度,其中SwinNet網絡在第3、第4組測試集中的精度更是達到了99%以上。

SwinNet網絡模型的測試集分類結果可以通過圖8的混淆矩陣更加直觀的展示。結合數據集的描述可以發現SwinNet網絡在4組不同測試集進行測試的結果中分別只有5、5、4、10個狀態類別被錯誤的分類。

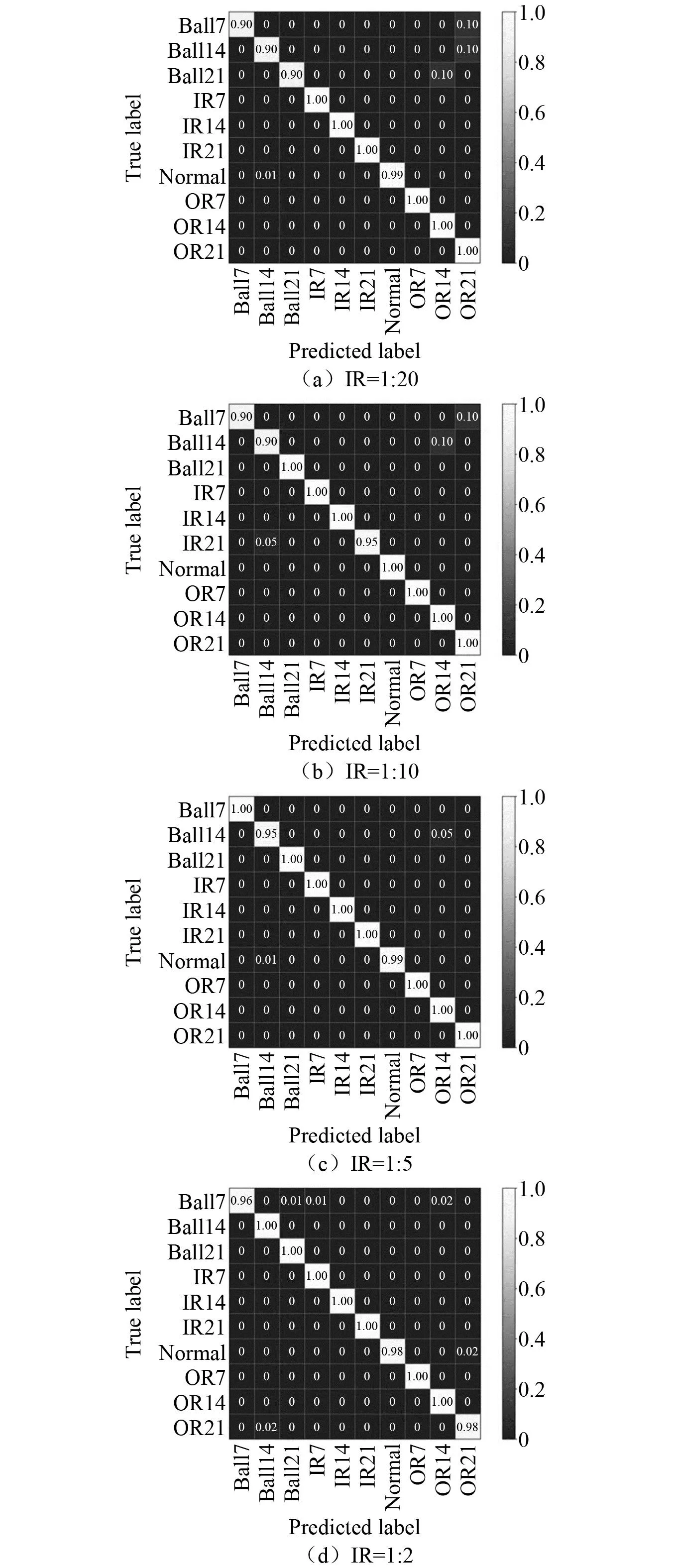
圖8 4組測試集混淆矩陣Fig.8 Confusion matrices for the 4 test sets

3.3 噪聲環境測試

機械設備在實際運行過程中通過傳感器采集到的振動信號往往攜帶環境噪聲,而CWRU數據集的振動信號所包含的噪聲級別還達不到“強噪聲”的程度。考慮到機械設備運行環境中,許多噪聲源的統計特性近似為高斯分布,而高斯白噪聲作為一種隨機噪聲能夠涵蓋多種頻率范圍內噪聲成分,因此使用高斯白噪聲來模擬真實環境中的復雜噪聲是一種較為有效的方式。為了評估SwinNet網絡在噪聲環境下的診斷性能,在4組原始失衡數據集中分別添加信噪比為-4～12 dB的高斯白噪聲,然后使用通過4組增強數據集進行訓練的模型來進行抗噪試驗。通過增強數據集訓練的模型的抗噪測試驗證結果如圖9所示。

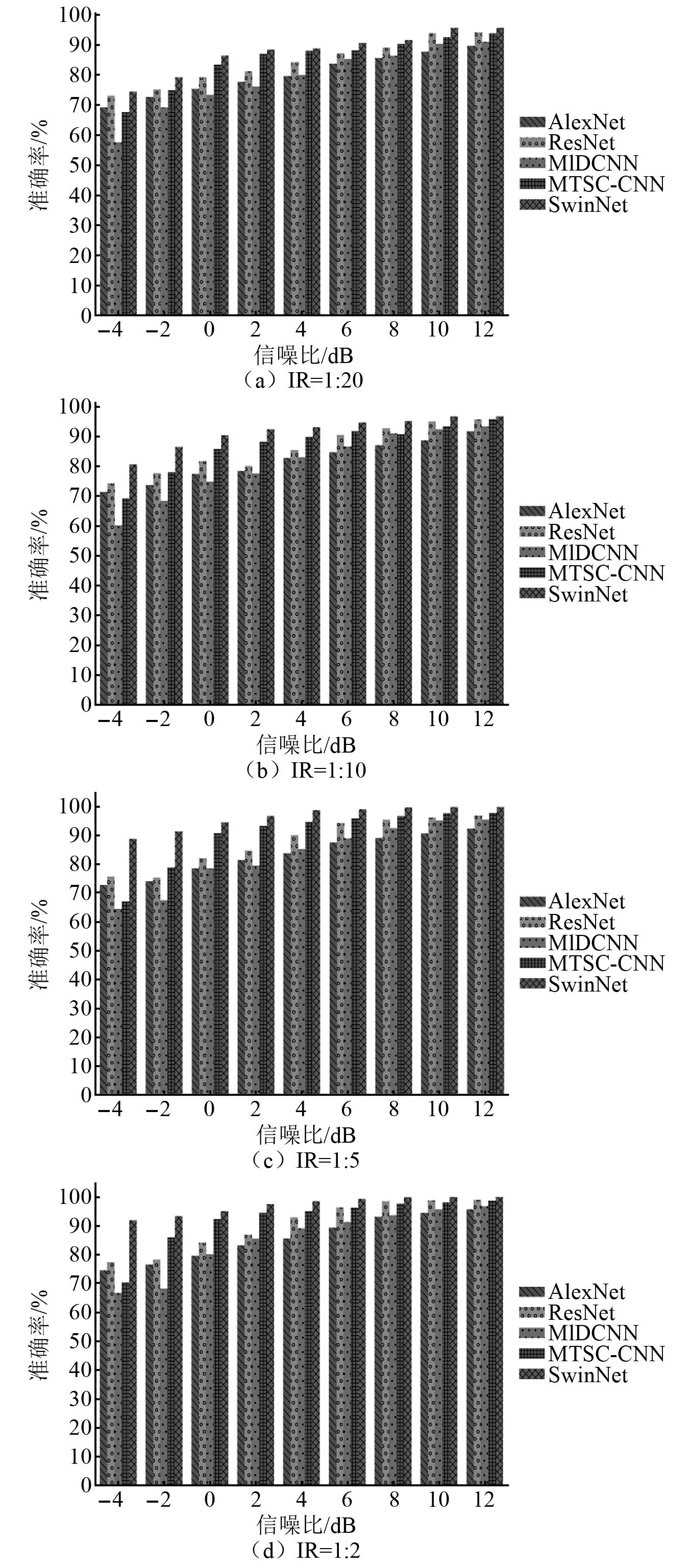
圖9 噪聲測試驗證結果Fig.9 The results of noise testing verification

使用MCIDA算法增強IR為1∶20的失衡數據集,通過該增強數據集進行訓練的模型抗噪測試具體值如表4所示。

表4 增強IR為1∶20的數據集訓練的模型的噪聲測試結果Tab.4 Noisy test results for a model trained on a dataset with an augmentation imbalance ratio of 1∶20

由圖9(d)可知,通過MCIDA算法對輕微失衡數據集進行數據增強后再訓練得到的模型的抗噪測試準確率最高,其中本文所提出的SwinNet網絡在信噪比為-4 dB時可以獲得超過90%的準確率,精度遠遠超過其他模型。隨著失衡數據集的失衡程度升高,雖然所有診斷算法可以通過使用MCIDA算法來增強其故障診斷精度,但是模型在“強噪聲”的影響下其精度還是會有不同程度的下降,通過圖9(a)再結合表4數據可知本文所提出的SwinNet網絡的故障診斷穩定性比其他所有模型都好。即使受到原始數據類別嚴重失衡與噪聲環境干擾的雙重影響,SwinNet網絡的診斷精度仍然高于其他模型,達到了74.45%。

為了驗證SwinNet網絡在更加極端的噪聲環境中診斷的有效范圍,針對失衡比值為1∶5與1∶2的原始數據集進行數據增強后進行訓練的SwinNet網絡進行更多信噪比場景下的抗噪測試,其結果如圖10所示。

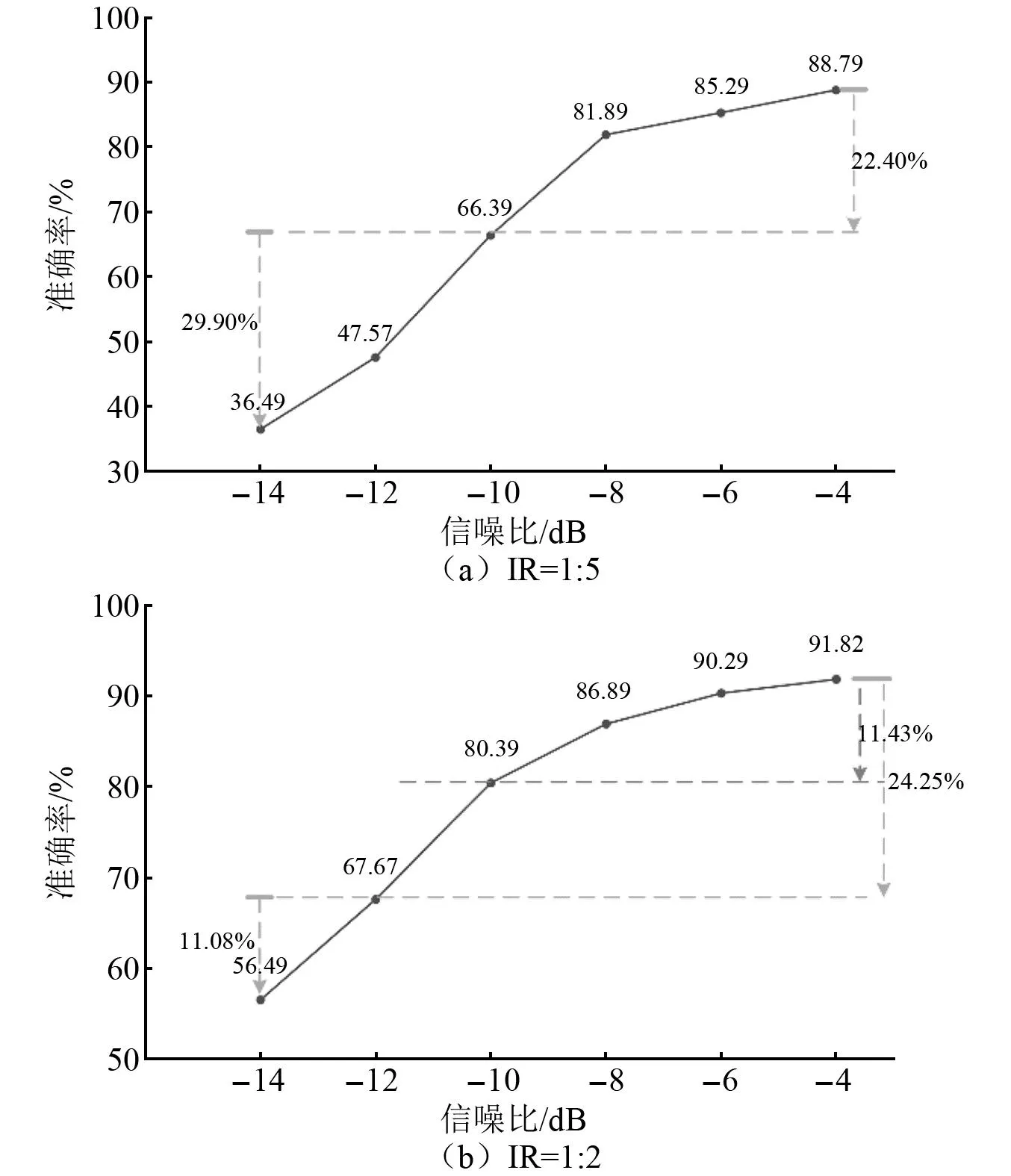
圖10 SwinNet網絡極端噪聲環境測試結果Fig.10 Testing results of SwinNet network under extreme noise environment

由圖10(a)可知,隨著噪聲的增加,SwinNet對故障信號的提取能力減弱。當信噪比為-10 dB時,其診斷精度相比于信噪比為-4 dB時下降了22.4%,但此時的精度可以達到66.39%,仍然是可以接受的水平,隨著信噪比下降到-14 dB,其診斷精度迅速下降了29.9%,可以認為此時SwinNet網絡不再具備故障診斷能力。由圖10(b)可知當原始數據集只有輕微失衡時,使用數據增強后再訓練獲得的SwinNet網絡在信噪比為-12 dB時的診斷精度為67.57%,仍然具有較強的診斷能力。究其原因是因為SwinNet模型擁有MSLRF層可以充分的提取二維時頻圖像的低維特征,同時擁有Swin Transformer編碼器的局部窗口機制與移動窗口機制,可以更加關注當前像素點相鄰的像素點,減少對噪聲或者異常數據點的關注,進一步提高模型的泛化能力。

3.4 噪聲標簽測試

在實際的故障數據采集過程中,經常由于人為操作失誤導致某些樣本被標記上錯誤的標簽,這種錯誤標簽被稱為噪聲標簽。為了驗證SwinNet網絡在樣本集輕微失衡且混入了噪聲標簽的情況下仍然具有很好的診斷精度,使用3.2節中的失衡比值為1∶2的失衡數據集來作為該試驗的原始數據集。由于實際故障診斷中不可能出現某類樣本集存在大量噪聲標簽的情況,因此在這里對原始數據集按照3∶1∶1的比例劃分出訓練集、驗證集、測試集后,將不添加噪聲標簽的訓練集記為A,而按照5%、8%、10%的噪聲標簽率(Label Noise Rates,LNR)對訓練集中的樣本進行替換后獲得的3組含有噪聲標簽的訓練集記為B、C、D,具體劃分細節由表5給出。

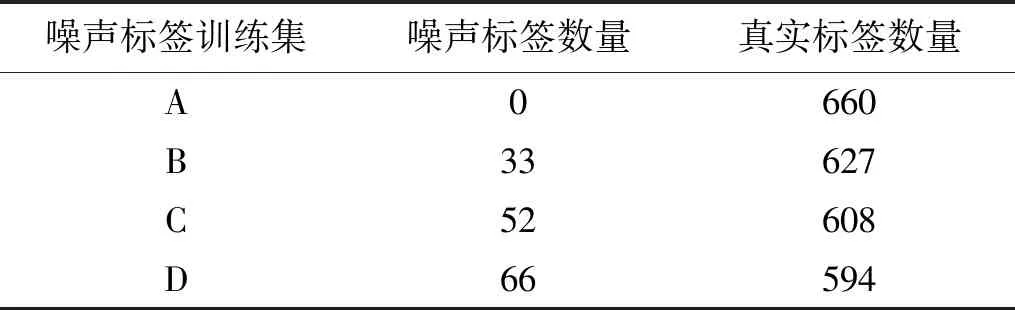
表5 4組噪聲標簽訓練集具體劃分展示Tab.5 4 sets of noise label training set specific division display

將SwinNet網絡與對比模型在4組含有不同噪聲標簽數量的訓練集中進行訓練,使用不含噪聲標簽的測試集對網絡模型進行測試,各個模型的測試集對比結果如表6所示。從表6中的結果可知在樣本集輕微失衡的情況下,錯誤的標簽占比確實會在一定程度上影響模型的故障診斷精度。隨著訓練集中噪聲標簽數量的增加,各個模型的診斷精度都呈現明顯的下降趨勢。結合圖11與表6可知,本文所提出的SwinNet網絡在樣本集輕微失衡且訓練集中混入了噪聲標簽的情況下診斷性能仍然表現優異。即使在訓練集噪聲標簽率為10%的情況下,其診斷精度仍然達到了98.12%,遠超過了其他的故障診斷模型的診斷精度。

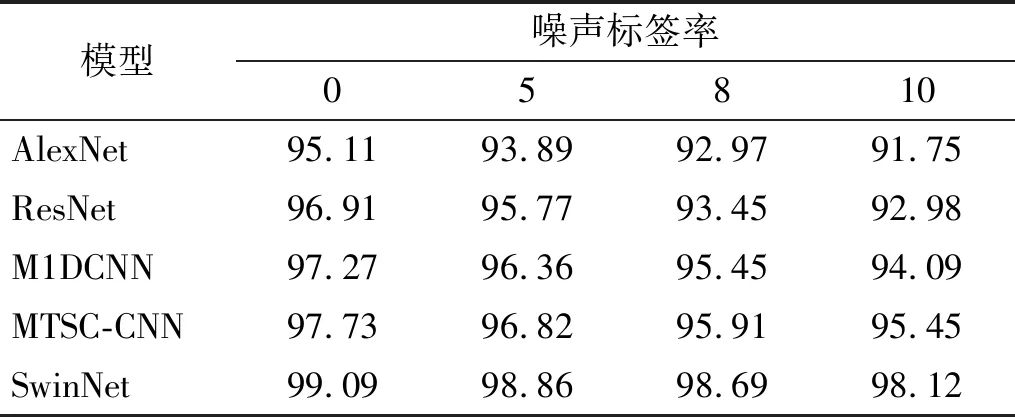
表6 不同噪聲標簽率下訓練的模型的測試集對比結果

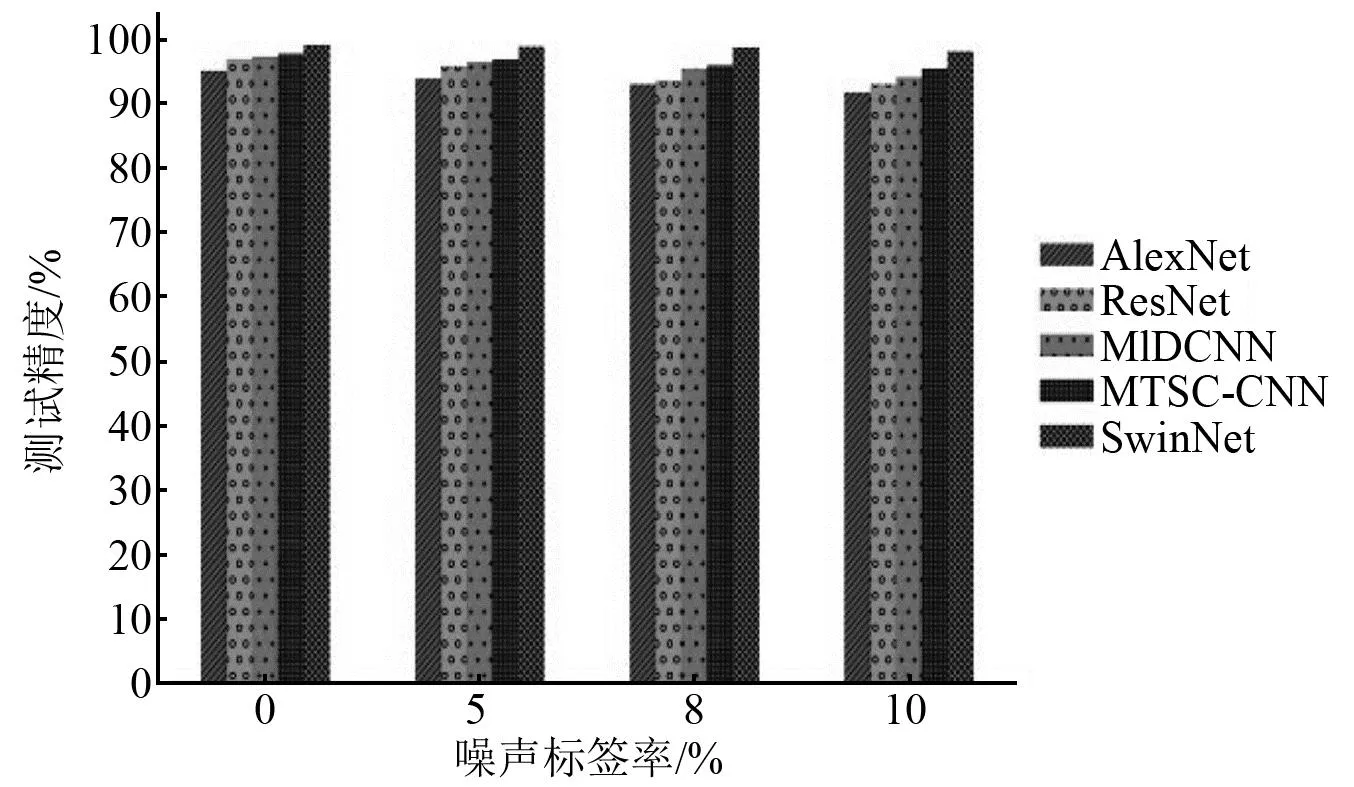
圖11 不同噪聲標簽率結果對比Fig.11 Comparison of results with different noise label rates

為了更加直觀地觀察SwinNet網絡的故障診斷效果,采用t-SNE技術可視化處理測試集樣本,獲得測試集的樣本特征分布如圖12所示。其中,圖12(a)是使用不含噪聲標簽訓練集訓練的SwinNet網絡對測試集進行分類后的可視化特征分布情況,圖12(b)～圖12(d)分別是使用噪聲標簽率為5%、8%、10%的訓練集訓練的SwinNet網絡對測試集進行分類后的可視化特征分布情況。

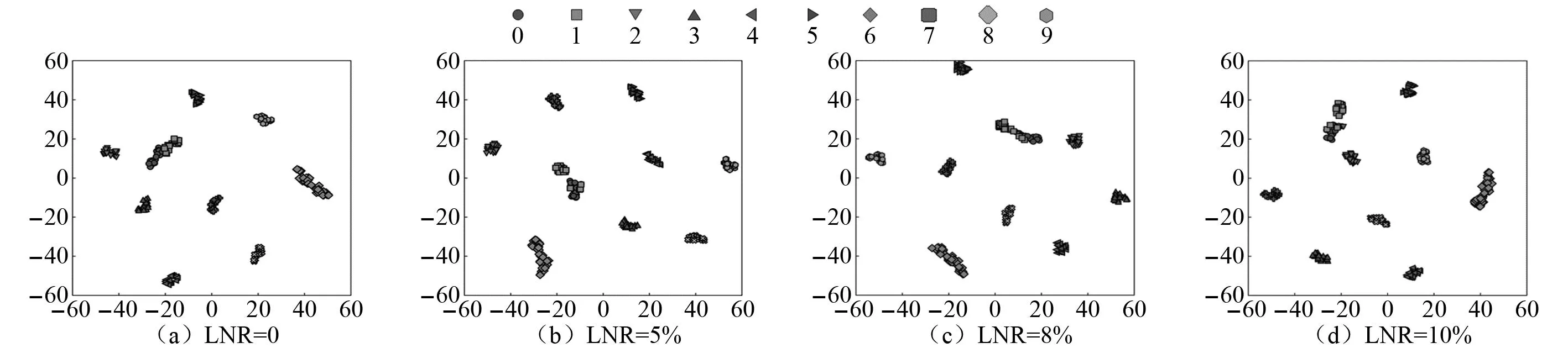
圖12 不同噪聲標簽率下t-SNE特征可視化顯示Fig.12 t-SNE feature visualization display under different noise label rates

由圖12可知,在樣本集輕微失衡且訓練集含有噪聲標簽的情況下,本文所提出的SwinNet網絡仍然可以將測試集中的樣本特征進行很好的分割。這充分說明了SwinNet網絡優秀的故障診斷能力,該網絡利用MSLRF 層對二維時頻信號進行特征提取后,借助移動窗口自注意力機制對輸入的圖像特征進行全局信息的建模,讓模型可以更好地學習到魯棒的特征表示,從而進一步提高模型的魯棒性。

4 結 論

針對在較為復雜的環境中對滾動軸承進行高精度的故障診斷問題,本文提出了一種將混合裁剪失衡數據增強算法與SwinNet網絡進行結合的故障診斷方法。具體結論如下:

(1) 提出了一種混合裁剪失衡數據增強(MCIDA)算法,利用該算法可以很好地解決滾動軸承故障診斷領域存在的故障數據類別失衡問題。

(2) 提出了一種SwinNet故障診斷網絡,該網絡與MCIDA算法進行結合使用能夠很好地應對診斷中存在的環境噪聲干擾與噪聲標簽干擾問題。

(3) 本文在公開數據集上做了大量仿真測試。結果表明,與現有方法相比本文所提出的方法故障診斷精度相對更高。

雖然本文所提方法在一定程度上提高了滾動軸承的故障診斷效果,但是在針對變負載條件下滾動軸承故障診斷方面還要做進一步研究。