中低速磁浮最小曲線半徑及緩和曲線長度研究

林遠揚, 李 苗, 馬衛華, 王 波, 張 敏, 左飛飛

(西南交通大學 軌道交通運載系統全國重點實驗室,成都 610031)

21世紀以來,我國在高速鐵路、重載鐵路、城市軌道交通和磁浮交通四大領域發展迅猛,取得了舉世矚目的重大成就[1]。日益完善的軌道交通網絡,為旅客出行帶來極大便利的同時,也進一步激發了人們的期望[2]。其中,中低速磁浮交通擺脫了傳統輪軌黏著的限制,且具有轉彎半徑小、爬坡能力好、選線適應性強等優點,受到許多國家的廣泛關注和持續研究[3]。線路參數作為中低速磁浮交通最基本的設計參數,其取值大小對于中低速磁浮交通的列車運行品質和建設成本具有重要影響。因此,科學合理地設計中低速磁浮交通的線路參數,是推動中低速磁浮交通發展中面臨的問題之一。

曲線半徑大小、緩和曲線長度是線路設計的關鍵參數,其在保證車輛運行效率的同時,還需要保證車輛具有優秀的乘坐舒適度,因此其研究受到國內外眾多學者的關注。在磁浮車輛的曲線半徑研究中,王相平等[4-5]通過仿真研究了小半徑曲線上的磁浮車輛-軌道耦合系統振動特性,得到車體、空氣彈簧等部件的動力響應。姚金斌等[6-7]從乘客舒適度、磁浮列車技術要求等方面對中低速磁浮線路最大橫坡角取值進行了分析,進而給出最小平曲線半徑取值。時瑾等[8]通過計算中低速磁浮車輛滑枕偏移距離、彈簧變形量等指標,對其最小平、豎曲線半徑展開了研究,并提出建議值。Jiang等[9]基于理論分析得到高速磁浮最小平曲線半徑理論值,并通過動力學仿真對其優化調整。在磁浮車輛的緩和曲線研究中,武巍[10]通過仿真研究了緩和曲線參數對中低速磁浮動力學性能的影響規律,得到了乘客舒適度隨緩和曲線類型及長度的變化關系。米隆等[11-12]基于行駛動力學理論,推導出適用于高速磁浮線路的平、豎緩和曲線長度計算公式,進一步提出其建議值。茍智平[13]參照高速輪軌鐵路線路參數的設計方法,對高速磁浮線路平面緩和曲線展開了研究,并得到一系列取值。Han等[14]利用建立的中低速磁浮列車模型分析了緩和曲線參數對列車懸浮穩定性的影響,得到懸浮穩定性隨緩和曲線參數的變化規律。

上述研究成果一定程度上促進了磁浮交通的選線設計,但目前中低速磁浮線路研究成果均為基于速度在100 km/h等級以下曲線半徑取值的研究,且多數研究僅通過受力分析得到最小曲線半徑取值,該方法將車輛視為質點,未考慮車輛中各部件之間的相對運動關系;對于緩和曲線的研究,則多集中在高速磁浮線路緩和曲線的取值,且上述研究均忽略了列車在緩和曲線上運行時受到的法向沖擊為空間曲線決定的法向沖擊和橫坡扭轉產生的法向沖擊的疊加。而中低速磁浮列車運行速度得到提升、系統結構復雜且線路緩和曲線類型不同于高速磁浮線路的一波正弦型,因此有必要開展中低速磁浮線路最小曲線半徑及緩和曲線長度的研究。

1 舒適度控制目標值

旅客舒適度是指列車運行時,車上旅客受到車體各種運動的作用后,在生理和心理上感覺不舒適的程度。由于中低速磁浮列車多采用“抱軌”的方式運行,降低了列車脫軌的風險。因此,旅客舒適度控制目標值是中低速磁浮列車線路參數選取的主要影響因素。列車行駛過程中會產生振動,在通過曲線路段時,車體會產生未被平衡的側向、法向離心加速度,當產生的離心加速度為0時,線路的曲率、橫坡角和列車的運行速度必須完美匹配,這較難實現。因此,CJJ/T 262—2017《中低速磁浮交通設計規范》[15]、TB 10630—2019《磁浮鐵路技術標準(試行)》[16]規定了其最大允許值來保證旅客乘坐的舒適度,各舒適度控制目標值如表1所示。

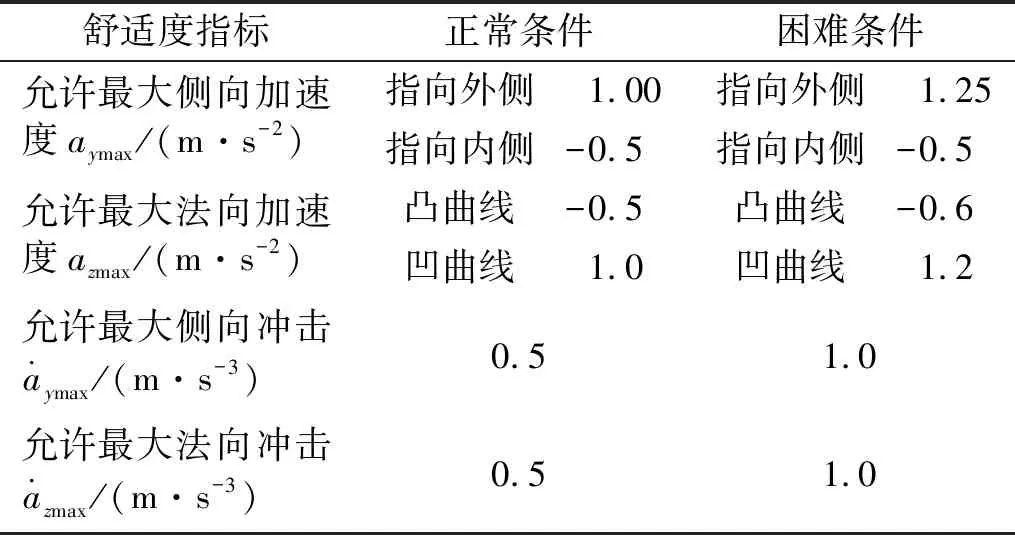
表1 舒適度控制目標值Tab.1 Comfort controls the target value

2 最小曲線半徑

曲線半徑是磁浮線路的關鍵參數之一,最小曲線半徑是指在規定的橫坡角、縱坡、行車速度等條件下,既保證列車在曲線路段時,產生的離心力等橫向力不超過軌道與車輛之間阻力所允許的限值,又能使車上旅客感覺舒適的臨界半徑。根據曲線線路相鄰兩坡段縱坡是否為0,曲線半徑可分為平曲線半徑和豎曲線半徑。

2.1 最小平曲線半徑

中低速磁浮列車通過空間曲線時的受力情況如圖1所示。圖1中:Y軸、Z軸分別平行、垂直于軌面;α、β分別為橫坡角、線路中心線的縱坡角;Re為空間圓曲線的半徑;m為中低速磁浮列車質量;g為重力加速度,取9.81 m/s2;FN為軌道對磁浮列車的反作用力;ay、az分別為磁浮列車在曲線上運行時受到的未平衡離心側向、法向加速度;FH、FV分別為磁浮列車通過平曲線、豎曲線時受到的離心力,FH、FV的計算公式為

圖1 中低速磁浮列車通過空間曲線時的受力情況Fig.1 The force on a medium- and low-speed maglev train as it passes through a spatial curve

(1)

(2)

式中:V為磁浮列車運行速度;RH和RV分別為平曲線和豎曲線半徑。

當列車通過曲線時,在Y軸方向的受力應滿足

may≥FVsinα+FHcosα-mgsinαcosβ

(3)

將FH、FV代入式(3)得到平曲線半徑計算公式

(4)

根據式(4)可見,中低速磁浮列車平曲線半徑的取值受列車運行速度、橫坡角、縱坡角、豎曲線半徑和側向加速度共同控制。當列車在平曲線上運行時,豎曲線半徑對平曲線半徑取值的影響可忽略,即RV取∞。圖2為橫坡角6°、側向加速度-0.5 m/s2和1.0 m/s2時,縱坡對平曲線半徑的影響。由圖2可以看出,當列車運行條件、速度相同時,隨著縱坡坡度的增大,平曲線半徑基本保持不變,因此可忽略縱坡對平曲線半徑取值的影響,即縱坡取0‰。將式(4)進一步簡化為式(5)

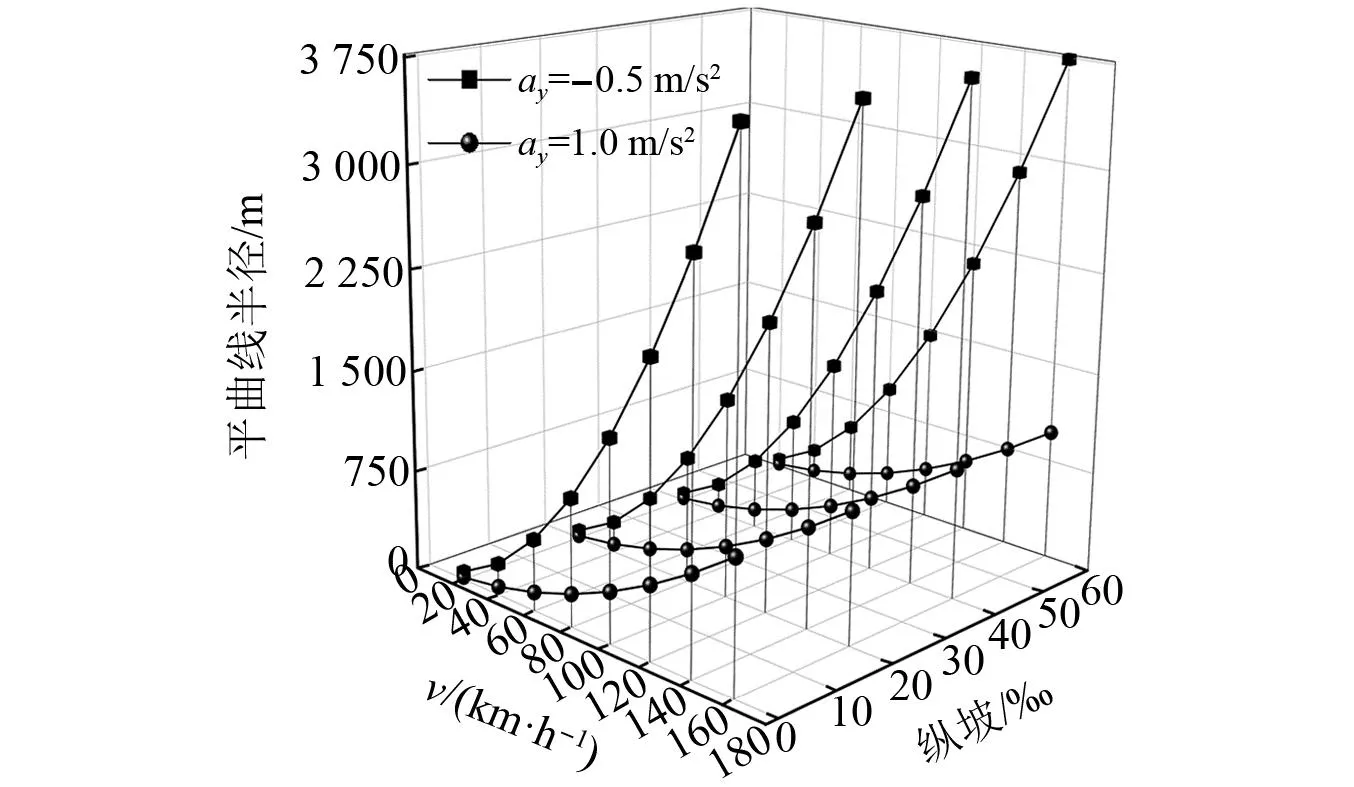
圖2 縱坡對平曲線半徑的影響Fig.2 Influence of longitudinal slope on radius of horizontal curve

(5)

根據CJJ/T 262—2017《中低速磁浮交通設計規范》的規定,中低速磁浮交通線路允許設置的最大橫坡角為6°。因此,考慮橫坡角為2°、4°、6°時,對中低速磁浮列車以20～160 km/h速度時的最小平曲線半徑展開計算。其中正常條件下,aymax取-0.5 m/s2、1.0 m/s2;困難條件下,aymax取-0.5 m/s2、1.25 m/s2,對正常和困難條件下各自對應的兩組計算結果進行比較,并取最小值,得到滿足舒適度要求的中低速磁浮列車最小平曲線半徑取值,如附錄A中表A.1所示。圖3為側向加速度控制下,速度、橫坡角與平曲線半徑的關系,由圖3可以發現,正常條件、困難條件下,指向內側的最大側向加速度確定的平曲線半徑取值遠大于指向外側的最大側向加速度確定的平曲線半徑取值,因此指向外側的最大側向加速度控制著最小平曲線半徑的取值;當列車通過平曲線速度一定時,橫坡角越大,中低速磁浮列車可允許通過的平曲線半徑越小。

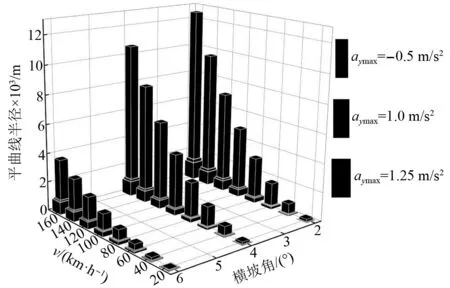
圖3 側向加速度控制下速度、橫坡角與平曲線半徑的關系Fig.3 Relationship between speed, cross slope angle and radiusof horizontal curve under lateral acceleration control

2.2 最小豎曲線半徑

當列車通過曲線時,在Z軸方向的受力應滿足

maz≥mgcosαcosβ+FHsinα-FVcosα-FN

(6)

其中,

FN≈mg

(7)

將FH、FV代入式(6)得到中低速磁浮豎曲線半徑計算公式

(8)

根據式(8)可見,中低速磁浮列車豎曲線半徑的取值受列車運行速度、橫坡角、縱坡角、平曲線半徑和法向加速度共同控制。當磁浮列車在豎曲線上運行時,平曲線半徑對豎曲線半徑取值的影響可忽略,即RH取∞。圖4為縱坡60‰、法向加速度-0.5 m/s2和1 m/s2時,橫坡角對豎曲線半徑的影響。由圖4可以看出,當磁浮列車運行條件、速度相同時,橫坡角對線路豎曲線半徑影響很小,可忽略,即橫坡角取0°。因此,將式(8)進一步簡化為式(9)

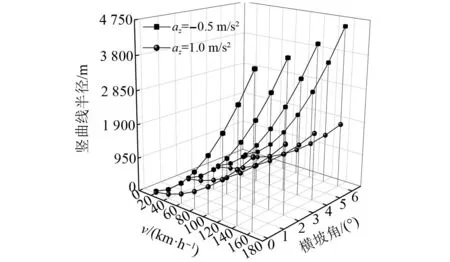
圖4 橫坡角對豎曲線半徑的影響Fig.4 Influence of cross slope angle on radius of vertical curve

(9)

根據CJJ/T 262—2017《中低速磁浮交通設計規范》的規定,中低速磁浮交通正線的最大縱坡不宜大于60‰。因此,考慮縱坡為20‰、40‰、60‰時,對中低速磁浮列車以20～160 km/h速度通過曲線時的最小豎曲線半徑展開計算。其中正常條件下,azmax取-0.5 m/s2(指向內側)、1.0 m/s2(指向外側);困難條件下,azmax取-0.6 m/s2、1.2 m/s2,對正常和困難條件下各自對應的兩組計算結果進行比較,并取最小值,得到滿足舒適度要求的中低速磁浮列車最小豎曲線半徑取值,如附錄A表A.2所示。圖5為法向加速度控制下,速度、縱坡與豎曲線半徑的關系。由圖5可以發現,凸曲線上法向加速度確定的豎曲線半徑取值遠大于凹曲線上法向加速度確定的豎曲線半徑取值,因此凹曲線上允許的最大法向加速度控制著最小豎曲線半徑的取值;在中低速磁浮交通正線規定的最大縱坡范圍內,縱坡對最小豎曲線半徑的取值幾乎無影響。

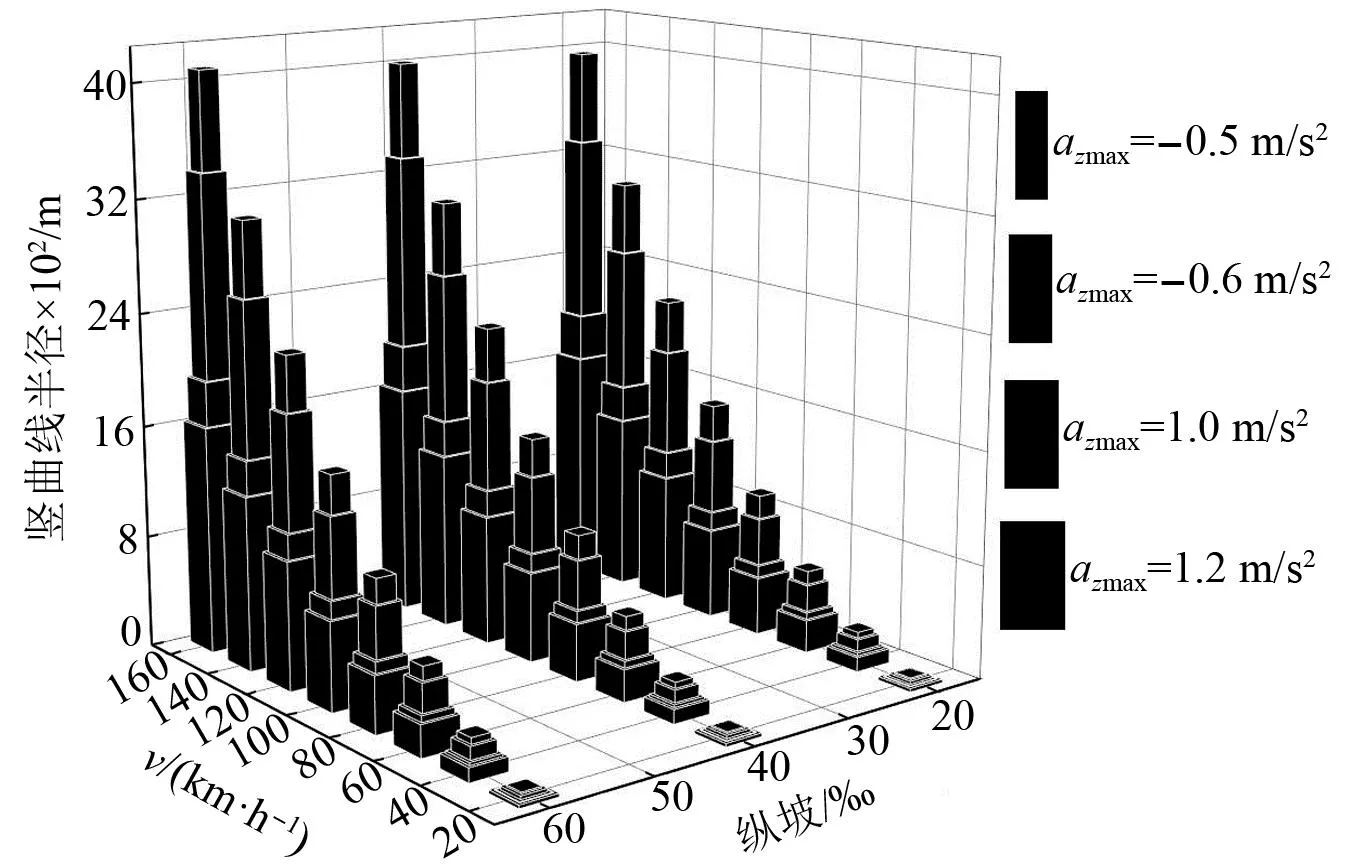
圖5 法向加速度控制下速度、縱坡與豎曲線半徑的關系Fig.5 Relationship between speed, longitudinal slope and radius of vertical curve under normal acceleration control

3 最小緩和曲線長度

緩和曲線是磁浮線路線形要素之一,在中低速磁浮線路縱斷面設計中,在相鄰兩坡度之間,一般不設置緩和曲線,故中低速磁浮交通緩和曲線為平面緩和曲線,它通常用于連接圓曲線和直線或兩個轉向相同且半徑差值較大的兩段圓曲線。為了使列車能夠在線路上平穩、安全地運行,國內外學者提出了很多類型的緩和曲線[17-18],如:三次拋物線型、五次曲線型、S曲線型、一波正弦型等。根據TB 10630—2019《磁浮鐵路技術標準(試行)》的規定,中低速磁浮交通線路采用三次拋物線型緩和曲線,其上任意一點處的曲率和橫坡角可表示為

(10)

(11)

式中:k0為圓曲線曲率;α0為圓曲線橫坡角;l為緩和曲線上任意一點到直緩點的曲線距離,0≤l≤ls,ls為緩和曲線長度。

3.1 側向沖擊確定的緩和曲線長度

當中低速磁浮列車在緩和曲線上運行時,其受到的側向加速度為

(12)

由于中低速磁浮交通線路橫坡角很小,不大于6°,因此,可將式(12)進一步簡化為式(13)

(13)

式中,ρ為角度制到弧度制的換算符。

若列車以勻速通過緩和曲線,則其受到的側向沖擊為

(14)

故滿足側向沖擊要求的最小平面緩和曲線長度為

(15)

3.2 法向沖擊確定的緩和曲線長度

當中低速磁浮列車在緩和曲線上運行時,可忽略豎曲線半徑、縱坡的影響,即RV=∞,β=0‰。同時考慮外軌超高角甚小,可得列車在緩和曲線上運行時受到的由曲線決定的法向加速度

(16)

若列車以勻速通過緩和曲線,則其受到的由曲線決定的法向沖擊為

(17)

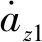
(18)

由橫坡扭轉產生的法向加速度應按式(19)計算

(19)

式中:bG為乘車區域最外側座位中心距線路中心線的側向距離,取1.5 m;αa為緩和曲線起點橫坡角;αe為緩和曲線終點橫坡角。

若列車以勻速通過緩和曲線,則其受到的由橫坡扭轉產生的法向沖擊為

(20)

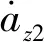
(21)

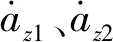
對式(22)進一步整理得式(23)

(23)

其中,

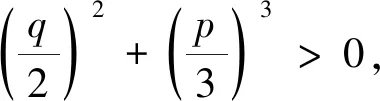
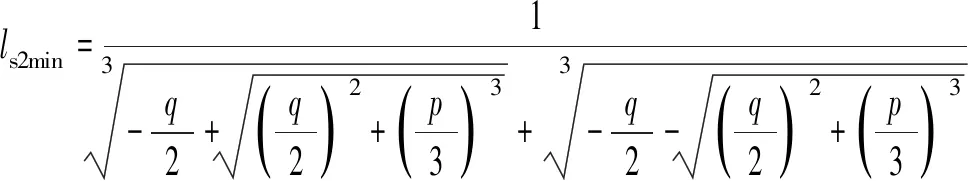
3.3 橫坡扭轉率確定的緩和曲線長度

因中低速磁浮交通線路采用三次拋物線型緩和曲線,其橫坡角在緩和曲線上的變化規律如式(11)所示,因此,列車通過平面緩和曲線時的橫坡扭轉率為

(26)

式中,Δα為橫坡扭轉率。

由式(26)可知,緩和曲線長度與連接的圓曲線橫坡角和緩和曲線上的橫坡扭轉率有關,根據CJJ/T 262—2017《中低速磁浮交通設計規范》中的規定,橫坡扭轉率在正常條件下不應大于0.12 (°)/m,困難條件下不應大于0.15 (°)/m,即正常條件下Δαmax=0.12 (°)/m,困難條件下Δαmax=0.15 (°)/m。所以,由橫坡扭轉率確定的平面緩和曲線最小長度為

(27)

綜上所述,3個因素共同決定中低速磁浮交通最小緩和曲線長度,最終的最小平面緩和曲線長度lsmin=max{ls1min,ls2min,ls3min}。考慮與緩和曲線相連的圓曲線橫坡角為2°、4°、6°,對中低速磁浮列車以20～160 km/h速度通過緩和曲線時的最小長度展開計算,其中與緩和曲線相連的圓曲線半徑大小分別取附錄A表A.1列車正常條件下運行時對應的建議值,中低速磁浮交通最小緩和曲線長度取值見附錄A表A.3。圖6為正常、困難運行條件下,側向沖擊、法相沖擊、橫坡扭轉率對緩和曲線長度取值的影響,由圖6可以發現,當橫坡角為2°,列車在正常/困難條件下以20 km/h速度運行時,最小緩和曲線長度受最大橫坡扭轉率控制,以40～160 km/h速度在正常條件下運行時,最小緩和曲線長度受最大側向沖擊控制,在困難條件下運行時,最小緩和曲線長度受最大法向沖擊控制;當橫坡角為4°,列車在正常/困難條件下以20～40 km/h速度運行時,最小緩和曲線長度受最大橫坡扭轉率控制,以60～160 km/h速度運行時,最小緩和曲線長度受最大法向沖擊控制;當橫坡角為6°,列車在正常/困難條件下以20～60 km/h速度運行時,最小緩和曲線長度受最大橫坡扭轉率控制,以80～160 km/h速度運行時,最小緩和曲線長度受最大法向沖擊控制。

圖6 不同因素對最小緩和曲線長度的影響Fig.6 The effect of different factors on the length of the minimum alleviating curve

4 動力學仿真

4.1 車輛模型

以三懸浮架的(懸掛)端置式中低速磁浮車輛為例,懸浮架結構呈“口字形”框架(如圖7所示),主要由2根縱梁、2個懸浮模塊、4片防側滾梁組成。

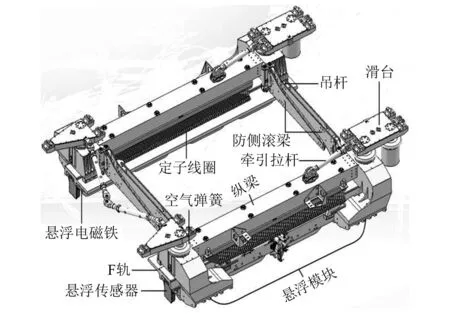
圖7 (懸掛)端置式懸浮架Fig.7 (Suspension) end-set levitation frame

車輛系統由1個車體、3個懸浮架、6個牽引桿、8個滑臺等部件組成,其中滑臺又分為端部移動滑臺和中部固定滑臺。當車輛通過曲線時,移動滑臺可以實現相應位置的懸浮架相對于車體發生橫向位移,發生橫向位移時,相應的懸浮架側架以固定滑臺為回轉中心。車體和懸浮架之間還安裝了迫導向機構,以此來改善車輛的曲線通過能力。對車輛結構進行適當簡化,基于Simpack軟件建立了具有如下微分代數方程形式的90自由度車輛系統動力學模型[19],如圖8所示,圖中各剛體的自由度說明見表2。

圖8 車輛系統動力學模型Fig.8 Vehicle system dynamics model

表2 車輛系統自由度Tab.2 Vehicle system degrees of freedom

(28)

式中:q為各剛體的廣義坐標;M為各剛體的質量矩陣;S為廣義慣量;Q為作用在各剛體上的廣義力矩陣;λ為拉格朗日乘子;Ф為約束雅可比矩陣;η為約束條件的加速度矢量。

4.2 懸浮控制模型

中低速磁浮車輛利用懸浮電磁鐵與F軌之間的電磁吸力實現車體懸浮,電磁力F為懸浮間隙δ與懸浮電磁鐵線圈電流i的函數[20]

(29)

式中:μ0為空氣磁導率;A為磁極正對面積;N為線圈匝數。

根據保角變換、四角幾何法[21]對式(29)分析可得懸浮力Fz、導向力Fy

(30)

(31)

式中:y為電磁鐵橫向位移;W為磁極寬度。

開環的電磁懸浮系統是不穩定的,遇到外部激擾時,系統容易失衡,因此需進行主動反饋控制。在實際的工程應用中,懸浮傳感器可檢測到懸浮電磁鐵端部的懸浮間隙、加速度信號,但無法獲得速度信號,懸浮間隙、加速度信號經濾波器處理后,還需引入狀態觀測器來重構懸浮間隙、加速度信號并構造速度信號[22]

(32)

(33)

(34)

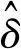
懸浮控制器利用狀態觀測器生成的懸浮間隙、速度和加速度信號生成控制電流

(35)

式中,k0、k1和k2分別為電磁鐵懸浮間隙、垂向速度和加速度反饋系數。

由式(29)～式(35),可搭建出懸浮控制系統流程圖,如圖9所示,工作時兩端相鄰線圈串聯在一起與懸浮控制器構成一套懸浮控制回路。

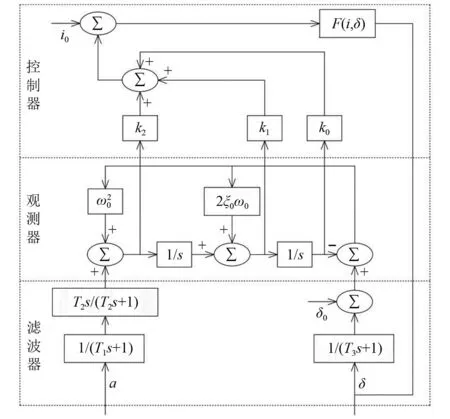
圖9 懸浮控制系統流程Fig.9 Suspension control system processes

4.3 工況設置

根據理論分析得到的最小曲線半徑和該半徑下推導得到的最小緩和曲線長度來設置線路進行動力學仿真,對其取值的可靠性進行逐一驗證,結果表明,中低速磁浮列車均能平穩地通過由上述參數設置的任意一組曲線工況。為避免贅述,本文以橫坡角6°,平曲線半徑970 m,緩和曲線長度120 m的曲線工況為例展開介紹,線路組成見圖10,與該線路匹配的中低速磁浮列車運行速度為160 km/h。中低速磁浮列車對軌道不平順引起的隨機激勵十分敏感,軌道不平順是磁浮交通主要的外部激勵源,加劇了車輛與軌道的相互作用,是造成車-軌耦合振動現象的重要因素。由于磁浮交通起步較晚,中低速磁浮軌道特殊“F”形結構也為軌道不平順的測量產生了一定限制,目前中低速磁浮軌道不平順的數據較少,還未形成統一的磁浮軌道不平順功率譜軌道不平順功率譜函數,因此本文選擇文獻[23]中的解析式(見式(36)),該解析式功率譜能很好的和實測線路譜相吻合,根據式(36)反演出本文仿真計算所需的軌道不平順樣本,如圖11所示,軌向不平順幅值在±2 mm內波動,高低不平順幅值在±4 mm內波動。

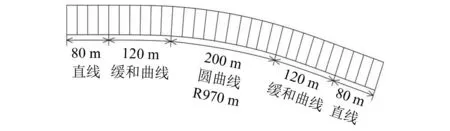
圖10 線路組成Fig.10 Line composition

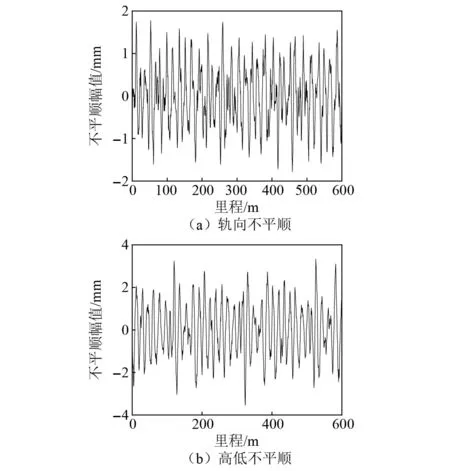
圖11 軌道不平順Fig.11 Track irregularity

(36)

式中:f為空間頻率;A、B、C、D、E、F、G為軌道譜特征參數。

4.4 結果與討論

以車體橫向和垂向振動加速度、電磁鐵懸浮間隙波動量和橫向位移、空氣彈簧橫向和垂向位移為評價指標,通過動力學仿真對車輛的曲線通過性能進行評估,進而判斷理論分析得到的中低速磁浮最小曲線半徑及緩和曲線長度取值是否可靠。

圖12所示為車輛以160 km/h的速度運行時車體的橫向和垂向振動加速度時間歷程曲線。圖12中,Car_F、Car_R分別為車體前、后側對應位置。

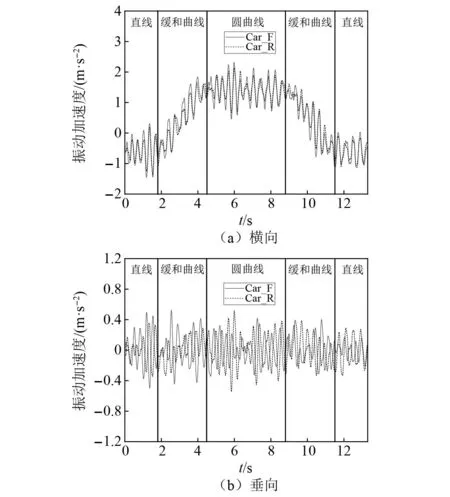
圖12 車體振動加速度Fig.12 Body vibration acceleration

從圖12可知,當車輛在圓曲線上運行時,車體橫向振動加速度達到最大,車輛在進圓曲線的緩和曲線上運行時,車體垂向振動加速度達到最大,且最大值均出現在車體前端,分別為2.32 m/s2、0.53 m/s2,進一步得到橫向、垂向平穩性最大值2.41、2.04,均小于2.5,表明車輛在曲線上運行時具有優秀的平穩性。

圖13所示為車輛以160 km/h的速度運行時電磁鐵的懸浮間隙波動量和橫向位移時間歷程曲線。圖13中,L11、L14/R11、R14分別為一位懸浮架左/右側懸浮模塊前、后端電磁鐵對應位置。

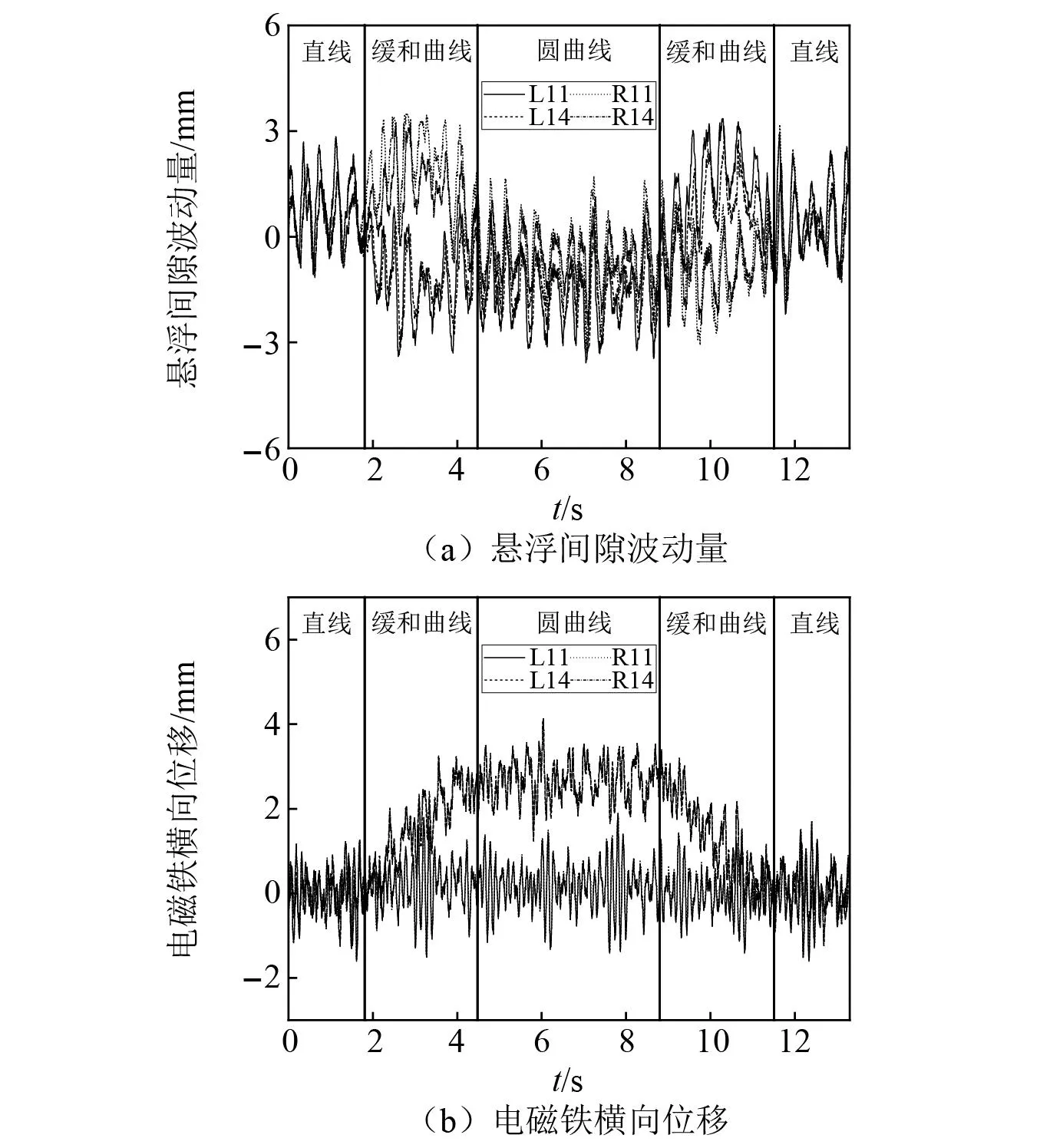
圖13 電磁鐵動態響應Fig.13 Dynamic response of electromagnet

計算結果表明,電磁鐵懸浮間隙波動量在-3.58～3.47 mm變化,在±4 mm以內,橫向位移最大值為4.12 mm,電磁鐵與F軌不會發生機械碰撞,表明車輛在曲線上運行時具有良好的懸浮穩定性和導向能力。

圖14所示為車輛以160 km/h的速度運行時空氣彈簧的橫向、垂向位移時間歷程曲線。圖14中,1LF、1LR/1RF、1RR分別為一位懸浮架左/右側縱梁前、后端空氣彈簧對應位置。

圖14 空氣彈簧位移Fig.14 The displacement of the gas spring

計算結果表明,當車輛在圓曲線上運行時,空氣彈簧橫向、垂向位移達到最大,空氣彈簧的橫向位移最大值為10.33 mm,出現在左側縱梁后端空氣彈簧上,垂向位移最大值為29.62 mm,出現在左側縱梁前端空氣彈簧上,空氣彈簧橫向、垂向位移均小于其限值。

綜上所述,車輛在曲線上運行時,具有優秀的平穩性和良好的懸浮穩定性、導向能力,空氣彈簧橫向、垂向位移均滿足規格要求。仿真結果表明,車輛曲線通過性能良好,曲線半徑及緩和曲線長度取值可靠。

5 結 論

通過上述研究,可以得到如下結論:

(1)中低速磁浮列車在正常、困難條件下運行時,最小平曲線半徑的取值受指向外側的最大側向加速度控制,最小豎曲線半徑的取值受凹曲線上最大法相加速度控制,當列車運行速度一定時,橫坡角越大,最小平曲線半徑取值越小,而縱坡對最小豎曲線半徑取值幾乎無影響。

(2)當橫坡角為2°,列車在正常/困難條件下以20 km/h速度運行時,最小緩和曲線長度受最大橫坡扭轉率控制,以40～160 km/h速度在正常條件下運行時,最小緩和曲線長度受最大側向沖擊控制,在困難條件下運行時,最小緩和曲線長度受最大法向沖擊控制;當橫坡角為4°,列車在正常/困難條件下以20～40 km/h速度運行時,最小緩和曲線長度受最大橫坡扭轉率控制,以60～160 km/h速度運行時,最小緩和曲線長度受最大法向沖擊控制;當橫坡角為6°,列車在正常/困難條件下以20～60 km/h速度運行時,最小緩和曲線長度受最大橫坡扭轉率控制,以80～160 km/h速度運行時,最小緩和曲線長度受最大法向沖擊控制。

(3)理論分析得到中低速磁浮列車以20～160 km/h速度運行時可通過的最小平、豎曲線半徑及緩和曲線長度,進一步給出其建議值,并通過動力學仿真對車輛的曲線通過性能進行評估,驗證了取值的可靠性,可為將來中低速磁浮交通的選線設計提供理論依據和數據參考。

附錄A

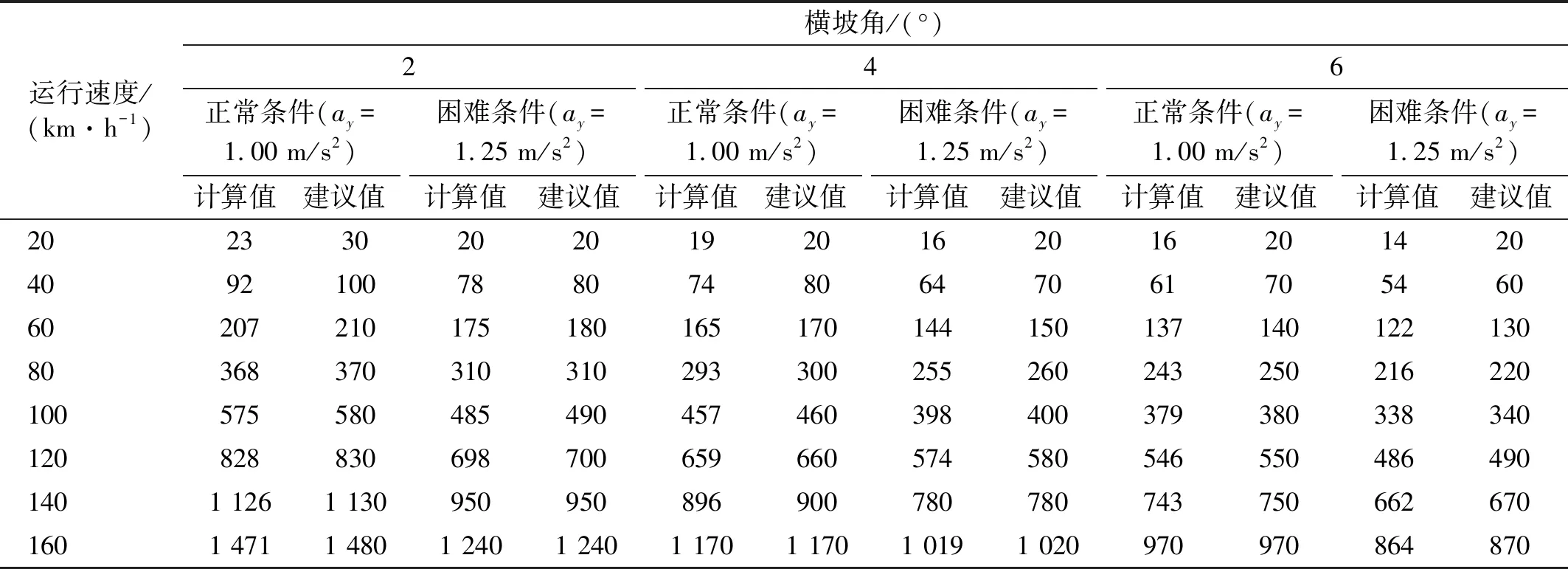
表A.1 中低速磁浮列車最小平曲線半徑Tab.A.1 The minimum flat curve radius for medium and low speed maglev trains 單位:m