碳排放權交易對試點地區綠色發展的影響及溢出效應
——基于PSM－DID 和SDID 模型的實證分析

余 謙 吳 婷 覃一冬 賈 鵬，2

1（武漢理工大學經濟學院，武漢 430070） 2（中交三公局第三工程有限公司，武漢 430033）

引 言

“二十大” 報告明確提出，“推動經濟社會發展綠色化、低碳化是實現高質量發展的關鍵環節”，要“發展綠色低碳產業，健全資源環境要素市場化配置體系”。為了實現經濟綠色高質量發展、達成雙碳目標，2021 年7 月份全國碳排放權交易市場正式上線。在這之前，自2013 年開始，碳排放權交易政策已歷經9 年試點。那么，在多年試點過程中，碳排放交易政策對綠色發展有什么直接影響？ 是否能通過促進試點地區產業升級和提高創新水平間接影響綠色經濟高質量發展呢？ 而碳排放交易對周邊地區的綠色發展又是否存在空間溢出效應呢？

基于上述問題，本文以碳排放權交易試點政策為出發點，用生態效率測度綠色發展水平，從不同維度區分了碳排放權交易試點對綠色發展的影響，包括碳排放權交易試點對綠色發展的直接效應、間接效應及空間溢出效應； 建立了碳排放權交易試點對綠色發展影響的理論框架，分析其影響機制，并設計實證模型進行驗證； 建立了PSM－DID模型和SDM－DID 模型，克服了傳統雙重差分模型只解決內生性而忽略了城市間的交互作用的問題。

1 文獻綜述

國內外有關生態效率的政策影響因素的研究主要分為三大類： （1） 關于低碳試點城市政策對綠色發展的影響的研究。王貞潔和王惠（2022）［1］研究發現低碳城市試點政策能顯著促進企業綠色發展； Cheng 等（2019）［2］研究發現低碳試點城市政策通過促進技術進步和提升結構效應能顯著促進綠色發展； （2） 創新型城市試點政策對綠色發展的影響研究。Li 等（2021）［3］發現創新型城市試點可以通過調整產業結構、充分發揮政府的直接干預作用對城市綠色發展產生積極影響； 劉曙光等（2022）［4］發現創新型城市試點政策還通過節能降耗和環境規制推動城市綠色發展； （3） 其他政策因素對綠色發展的影響研究。Jiang 和Tan（2020）［5］發現政府環境審計可以顯著改善靜態的和動態的生態效率； 辛寶貴和高菲菲（2021）［6］發現生態文明試點政策能顯著促進生態效率增長； 馬雙和海駿嬌（2022）［7］發現城市層面的環境政策能通過強化技術關聯性來促進區域生態效率增長，而省級層面的環境政策對技術關聯性反而有抑制作用。

關于碳排放權交易試點政策（Carbon Emissions Trading Pilot，CETP）的研究，主要是使用雙重差分法或其擴展模型對綠色創新效率、能源效率和碳排放效率等綠色指標進行政策效應評估。Hong等（2022）［8］研究發現CETP 能通過促進綠色創新和優化資源配置顯著提升城市單要素和全要素能源效率，高市場化和產業集聚更有利于能源效率的提升； Chen （2021）［9］發現CETP 主要通過技術進步、綠色創新和能源消費結構優化3 個途徑顯著提高試點城市的碳排放效率，市場化程度較高的城市作用更為明顯； 張揚等（2022）［10］發現CETP 能降低企業債務融資成本，進而促進實質性綠色創新。除上述研究之外，也有部分學者對CETP 與生態效率之間的關系展開了研究，Wu（2022）［11］研究發現CETP 對農業生態效率有顯著影響，張優智和喬宇鶴（2021）［12］研究發現CETP對試點地區的生態效率有顯著的促進作用。

隨著全球價值鏈低碳化發展趨勢日益明顯，現有研究不能滿足新常態下產業空間結構優化與經濟綠色高質量發展的需求，主要存在以下兩方面的局限性： （1） 現有研究分析碳排放權交易試點政策對綠色發展的全面效應并解釋其中的作用機理在因果推斷方面存在不足； （2） 有關綠色發展政策沖擊的研究主要采用傳統DID 模型，較少考慮到綠色發展的空間相關性，忽略了兩者的空間溢出效應。

2 理論假設

碳排放權交易試點對綠色發展具有直接效應是指CETP 能夠直接促進城市綠色發展。本文用生態效率衡量綠色發展，這一指標最早由Schaltegger和Sturm （1990）［13］提出，指某地區在一定時間范圍內產值增加額與要素投入和環境污染的比值，兼具“經濟增長” 效應和“污染減排” 效應。Costantini和Mazzanti（2011）［14］基于波特假說理論，發現合適的環境規制政策會吸引資本、勞動等生產要素的集聚，從而能改善該地區的資源配置效率。而CETP 作為限制性環境規制的一種，可能會促進資源配置的改善，從而提升經濟發展水平，實現“經濟增長”； 另外，CETP 會增加企業的碳排放成本，最終達到降低二氧化碳排放量的目的，具有“污染減排” 效應，能夠提高生態效率。

綜上，提出假設1： CETP 兼具“經濟增長”和“污染減排”效應，能夠直接促進城市綠色發展，即碳排放權交易試點對綠色發展具有直接效應。

碳排放權交易試點對綠色發展具有間接效應是指CETP 能通過促進技術創新和產業結構升級從而間接提升城市綠色發展水平。有研究表明，CETP 能促進產業結構的優化升級［15］、提升綠色技術創新水平［16］。產業結構調整是影響經濟發展的重要因素，技術創新是促進經濟發展的主要動力［17］，因此，CETP 可能通過促進產業結構優化升級或綠色技術創新間接影響綠色發展。碳排放權交易可以通過增加債務融資成本，從而迫使企業積極投入綠色創新研發，提升其綠色創新水平。低碳環保企業由于碳排放量較少，企業超額成本較低，且能通過交易市場出售多余的碳配額獲取低碳轉型的紅利，從而更有動力將資源用于技術研發和創新，進一步提升了其市場競爭力，獲取更多超額利潤。同時，對于高污染企業，短期內企業無法快速對生產設備和生產流程進行優化調整來達到固定排放配額，所需碳配額往往會超出固定排放配額。因此高污染企業需要通過市場交易獲取碳配額，這將導致生產成本提高。長期來看，高污染企業會選擇引進先進生產設備、加快低碳技術的研發或更換低碳低污染型生產要素或來降低生產成本。因此，無論是短期還是長期，企業所進行的綠色技術創新，不僅能提高環境收益，還能提高生產過程中的生產效率和經濟收益，降低生產成本，提高綠色發展水平； 與此同時，碳排放權交易機制能利用市場價格發現機制，以引導企業調整經營戰略，改變試點地區的產業結構布局。當企業獲得的碳排放權交易收益超過實施低碳技術改造或技術創新的成本，就會有更多資金流入綠色低碳技術研發和應用的環保企業，從而推動產業轉型升級，促進地區產業結構高級化，對綠色發展產生正面影響。

基于以上分析，提出假設2： CETP 能通過促進技術創新和產業結構升級間接提升城市綠色發展水平，即碳排放權交易試點對綠色發展具有間接效應。

碳排放權交易試點對試點地區的綠色發展具有溢出效應是指CETP 對試點城市周邊地區的綠色發展有顯著影響。有研究表明，CETP 對綠色創新［18］、碳排放量［19］的影響存在溢出效應。因此，CETP 也可能對試點地區周圍的生態效率有溢出效應。（1） CETP 會對周邊城市產生“污染避難所效應”。不同地區之間的環境規制差異，會導致污染企業向低管制地區轉移，使該地區成為污染避難所［20］。由于碳排放權交易會使試點地區的排污成本上升，當污染密集型產業增加額外的排放成本時，能源密集型和污染密集型工廠將趨向于向環境標準較低的非試點地區轉移，這會導致非試點地區的生態效率下降； （2） CETP 還具有“虹吸效應”。試點地區多是經濟密度高、資源稟賦強的一、二線城市，而CETP 還將進一步促進試點地區的產業結構升級和創新發展，賦予試點地區的新的競爭優勢，因而會吸引勞動力等生產要素和創新因素向試點城市集聚，不利于周邊地區的基礎設施建設和人力資本積累，阻礙了周邊地區的創新發展，進而影響生態效率； （3） CETP還會對周邊地區帶來“技術溢出效應”。CETP 誘導的高效節能和低碳技術可以推廣到非試點地區，根據內生創新理論［21］，技術創新造成的競爭效應和技術溢出使周邊地區可以以相對低廉的成本掌握技術創新的成果，促進周邊地區低碳生產技術的提升，從而促進生態效率增長。同時，根據區域增長極理論，試點地區創新水平提高帶來的綠色發展水平提升會通過不同途徑向創新水平低的非試點地區擴散。

綜上，本文提出假設3： CETP 對試點城市周邊地區生態效率具有空間溢出效應，“污染避難所效應”、“虹吸效應” 與“技術溢出效應” 的大小決定其方向和大小。

3 實證研究設計

3.1 空間權重矩陣的選擇

為了體現樣本個體間的空間聯系，考慮到樣本點間的地理距離，本文選擇了地理距離權重矩陣①作為模型估計的主要空間權重矩陣。由于空間計量模型的結果可能受到空間權重矩陣的影響，本文還將使用鄰接矩陣②和經濟地理距離權重矩陣③來檢驗空間計量實證結果的穩健性。為了減少或消除不同區域之間的外部因素的影響，本文對權重矩陣進行了行標準化處理。

3.2 模型設定

（1） 多期DID 模型

根據假說1，本文將CETP 作為一項準自然實驗，將實施CETP 的8 個試點區域覆蓋的地級市視為處理組，其他地級市視為對照組，多期DID模型設定為：

式中，GML是NT*1 維被解釋變量，emi是一個啞變量，表示碳排放權交易試點的情況；u為城市固定效應；v為時間固定效應；X為NT*k維控制變量矩陣；ε為是一個NT*N維的誤差項向量，β是待估參數，γ是將X連接被解釋變量的函數。

（2） 中介效應模型

根據假設2，碳排放權交易試點可能通過促進產業結構升級和技術創新，進而促進城市生態效率的增長。據此，參考溫忠麟和葉寶娟（2014）［22］的研究，使用中介效應模型驗證CETP 對綠色發展的間接效應，結合式（1），模型設定如下：

其中，M表示中介變量；θ為核心解釋變量對中介變量M的效應；a是在控制了自變量的影響后，中介變量M對被解釋變量的效應。如果系數θ和a均顯著，則說明間接效應存在，否則，應該使用Bootstrap 法檢驗H0：θ*a＝0，采用Bootstrap 檢驗如果置信區間不包含0，則系數乘積顯著，說明存在部分中介效應，否則，則說明不存在間接效應。

（3） SDID 時空效應模型

基于假說3，為準確地分離出CETP 對鄰近區域影響的凈效應，本文將空間滯后項引入多期DID 模型。DID 模型的一個經典假設是個體處理效應穩定性假設（SUTVA），即總體中的任何個體都不會受到其他個體接受處理與否的影響［23］。然而，在空間研究中，我們通常需要考慮到區域是相互關聯的。這就產生了影響在生產發生的區域（處理組）和周圍區域（對照組）上傳播的可能性，違反了SUTVA 假設，這使得因果推斷更加困難。因此，必須將政策的影響效果也模擬在與處理組相鄰的對照組上。在式（1） 的基礎上構建雙重差分模型的空間擴展形式（SDID）：

其中：W為空間權重矩陣；α為被解釋變量的空間自相關系數；β2為碳排放權交易政策的溢出效應；δ為其他控制變量的溢出效應；λ為隨機誤差的空間自相關系數，其他變量同式（1）。β2W*emi表示CETP 對處理組和對照組城市的間接影響的平均效應。

（4） SDID 模型的具體形式

根據Andre （2016）［24］的方式，對W矩陣進行分解：

其中，DD＝diag（emi）是一個N*N維矩陣，主對角線元素為處理效應（emi），其他元素為0，DC＝diag（I－emi），I是單位矩陣。代入式（5）中，可得到有約束模型：

通過構建WT，NT和WNT，NT為0 矩陣，則無約束模型為：

4 變量設定與數據來源

4.1 被解釋變量

本文選用生態效率測度綠色發展水平，采用基于SBM 方向距離函數的GML 指數，結合非期望產出SBM 模型和超效率SBM 模型，建立非期望產出－超效率SBM 模型，來測算城市的生態效率。選取的投入產出指標中，投入指標包括勞動力投入、資本投入和能源投入，分別使用全市年末從業人口（萬人）、固定資產資本存量、能源消耗量來衡量。其中，固定資產資本存量Ki，t采用永續盤存法估計，折舊率設為10.96%［25］，基期資金存量K0使用Hall 和Jones （1999）［26］提出的公式計算，如下：

能源消耗量是以標準煤折算方法折算后的全社會用電量，計算公式為：

期望產出指標使用以2003 年為基期，用城市對應省份的消費價格指數對城市名義GDP 進行平減所得的實際GDP，非期望產出是以熵值法測度的城市工業二氧化硫排放量（萬噸）、工業煙塵排放量（萬噸）、工業廢水排放量（萬噸）的綜合指標。

4.2 核心解釋變量

碳排放權交易試點（emi），emi為treat和post的交互項，若城市屬于碳排放權交易的試點城市，則treat＝1，否則為0； 碳排放權交易政策實施后，post＝1，否則取值為0。

4.3 控制變量

基于以往研究，本文選取4 個控制變量包括外商投資水平（fdi）、稟賦結構（str）、人力資本水平（capital）和經濟發展水平（eco）。外商投資水平（fdi）通過當年匯率平減后的實際利用外資金額占GDP 的比重測度； 稟賦結構（str）是當年資本存量與年末從業人數的比值，用來衡量一個地區要素稟賦豐裕的程度； 人力資本水平（capital）用當年在校大學生數占地區總人口的比重來衡量； 經濟發展水平（eco）則用地區人均GDP（萬元）來代表。

4.4 中介變量

本文的中介變量包括技術創新和產業結構升級。技術創新（tec）采用科學技術支出占地方一般公共預算支出的比例來表示。產業結構升級（ind）采用產業結構高級化指數表示，具體計算公式如下：

本文選用2003 ～2021 年全國共273 個地級市的面板數據作為研究對象，其中，剔除掉樣本缺失值過多的城市——貴州省轄下的畢節市、青海省轄下的海東市、寧夏回族自治區轄下的銀川市等20 個地級市以及中國港澳臺地區的樣本信息。本文數據來源于2004 ～2022 年各城市《城市統計年鑒》、各省（區、市）的統計年鑒、《中國環境統計年鑒》 和國家統計局官網，缺失的數據使用插值法補充。同時，為了消除異方差，在回歸過程中，對各指標作對數處理。各變量的描述性統計見表1。

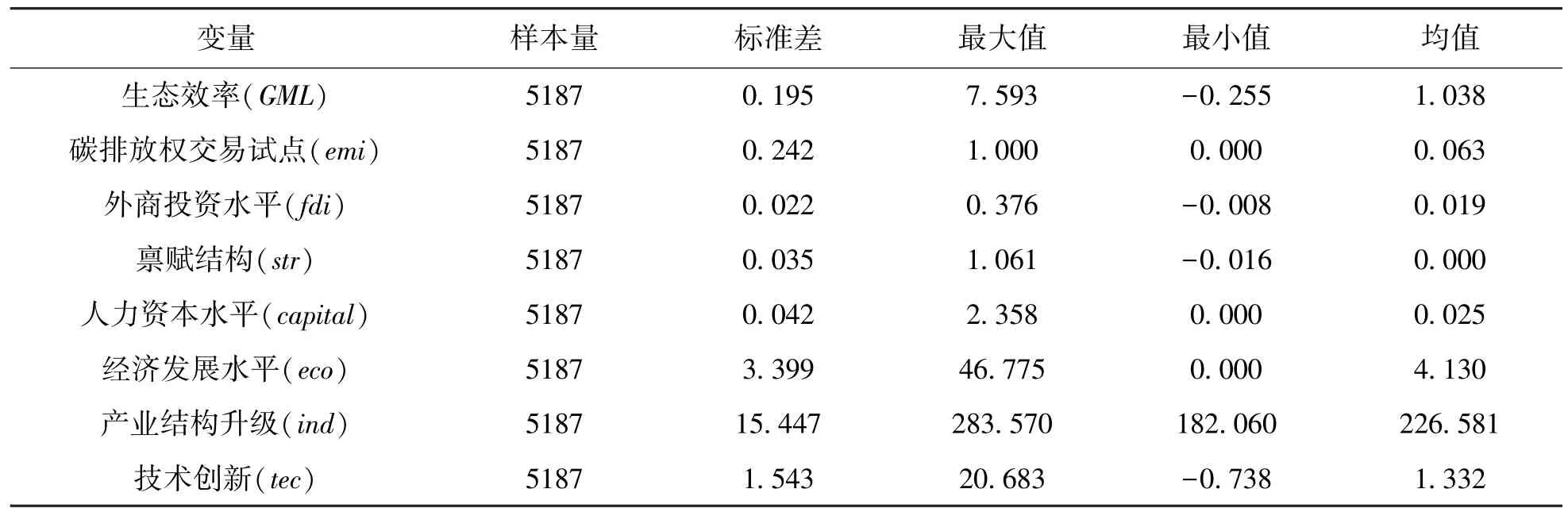
表1 變量的描述性統計

5 直接效應分析

5.1 PSM 有效性檢驗和平行趨勢檢驗

為了消除或減少選擇偏差，使處理組和對照組在各方面特征上盡可能相似，本文將采取傾向得分匹配（PSM）和DID 結合。將外商投資水平、稟賦結構、人力資本水平和經濟發展水平作為匹配協變量，進行Logit 回歸后，計算城市的傾向匹配得分，按照1 ∶3 的比例進行近鄰匹配，PSM 有效性檢驗見表2。可以看出，匹配前，外商投資水平和經濟發展水平的結果均顯著，說明處理組和對照組存在顯著差異。匹配后，協變量的t 檢驗結果均不顯著，說明協變量匹配后處理組和對照組不存在差異，PSM 結果有效。

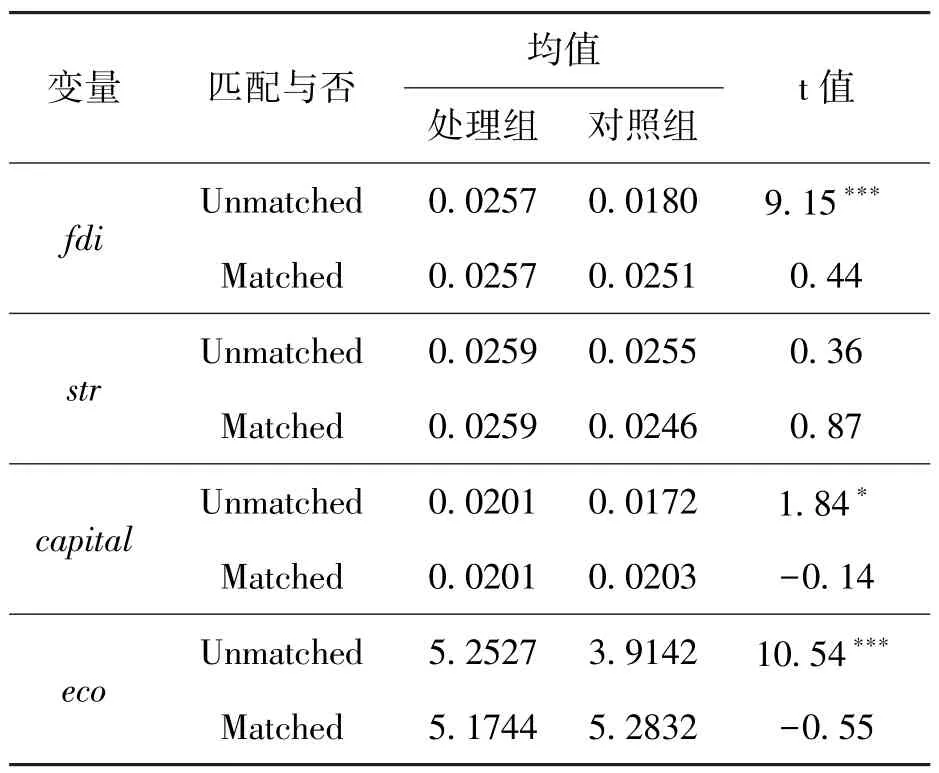
表2 PSM 有效性檢驗

平衡性檢驗見圖1。圖中可以看出，匹配前控制組和處理組的偏差較大，經濟發展水平、外商投資水平的偏差甚至達到30%以上，而匹配后各協變量處理組和對照組的偏差均小于10%，匹配前后控制組和處理組的偏差顯著降低，與表2的結論一致，匹配質量較好。

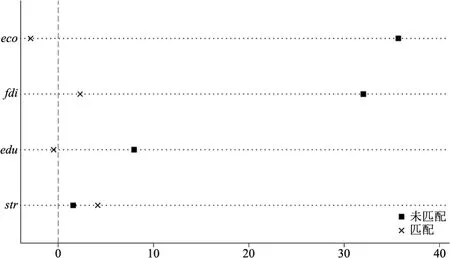
圖1 平衡性檢驗

在此基礎上進一步進行雙重差分估計。雙重差分模型的一個重要前提是處理組和對照組要滿足平行趨勢假設。本文采用事件研究法，選擇CETP 實施前3 期和實施后5 期，估計各期的效應④。估計結果基本滿足平行趨勢假設。

5.2 基準回歸

基準回歸結果見表3，可以看出，在控制了城市和時間雙向固定效應后，模型（1）～（4） 中emi的系數均為正且至少在10%的顯著性水平下顯著，說明CETP 顯著促進了試點城市的生態效率提升，CETP 對綠色發展有直接效應，驗證了假設1。此外，對于控制變量，模型（2） 和模型（4） 中經濟發展水平和外商投資水平均對綠色發展無明顯影響，稟賦結構對綠色發展產生了顯著的負面影響，但人力資本水平在模型（2） 中顯著為負，而在模型（4） 中不顯著，說明傾向得分匹配改變了人力資本水平的顯著性。

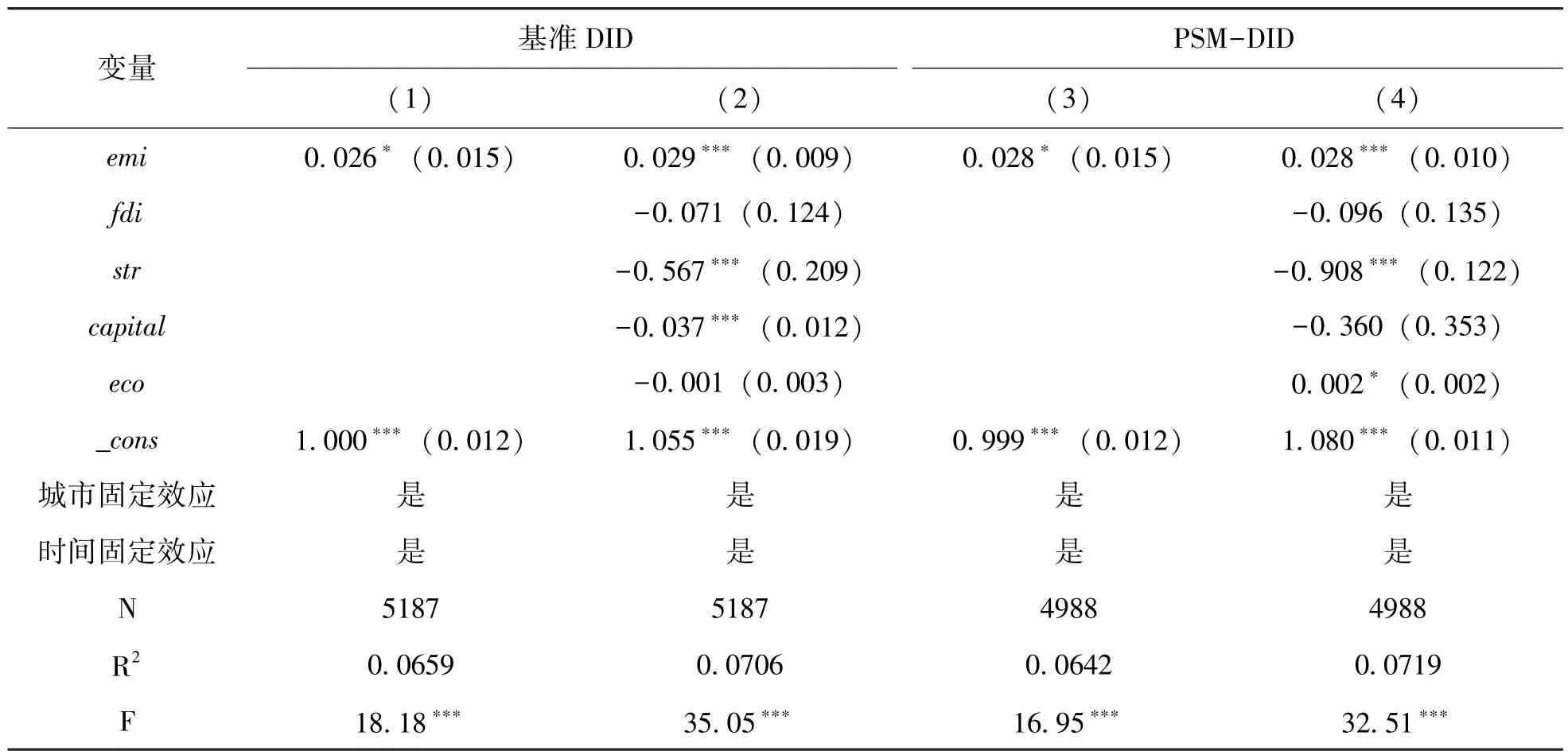
表3 DID 模型回歸結果

5.3 穩健性檢驗

（1） 安慰劑檢驗

為了驗證本文得到的實驗結論不受其他不可觀測因素的影響，需要進行安慰劑檢驗。具體操作如下： 本文在所有樣本中隨機選擇44 個城市作為虛擬實驗組，其余229 個城市作為虛擬對照組，進行基準回歸，并提取回歸后的核心解釋變量系數及標準誤，據此計算t 值，隨機進行上述模擬抽樣1000 次，繪制核心解釋變量的核密度分布圖，如圖2 所示。可以看出圖中絕大多數的系數和t 值均集中分布在0 附近，均值與真實值的距離較遠，且絕大多數估計系數并不顯著，這意味著CETP 對綠色發展的政策效應沒有受到其他未被觀測因素的影響。因此，實證結論是穩健的。

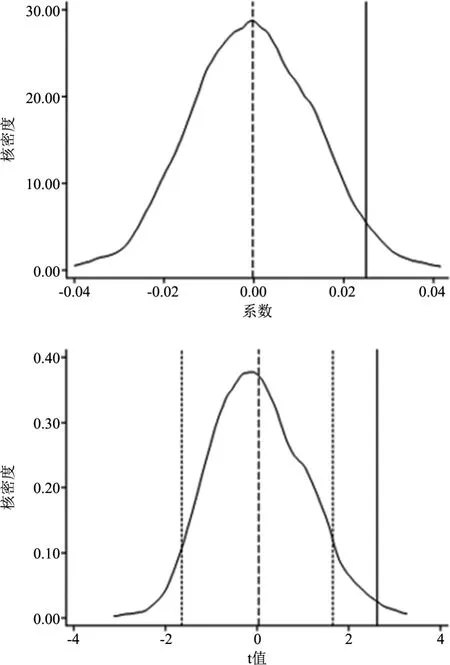
圖2 安慰劑檢驗

（2） 改變PSM 匹配方法

PSM 近鄰匹配比例的不同可能會對結果造成影響，為了避免這種可能性，本文調整PSM 近鄰匹配比例為1 ∶2 和1 ∶4。同時，上文在進行PSMDID 時所采取的是混合匹配方法，是指將多期的面板數據當作截面數據來匹配，這里將使用逐期匹配方法重新進行傾向得分匹配來驗證前文結果的穩定性。選擇政策實施前4 期，將每一期的處理組和對照組個體分別按照1 ∶1 的比例進行近鄰有放回匹配，并進行DID 回歸，結果見表4。可以看出，模型（1）～（6） 中，無論加入控制變量與否，核心解釋變量emi的系數始終為正且至少在10%的水平下顯著，而系數與基準回歸結果（0.026）并無較大差異，說明CETP 對生態效率影響顯著為正，近鄰匹配比例的大小和匹配的方法并不影響最終的實驗結論。

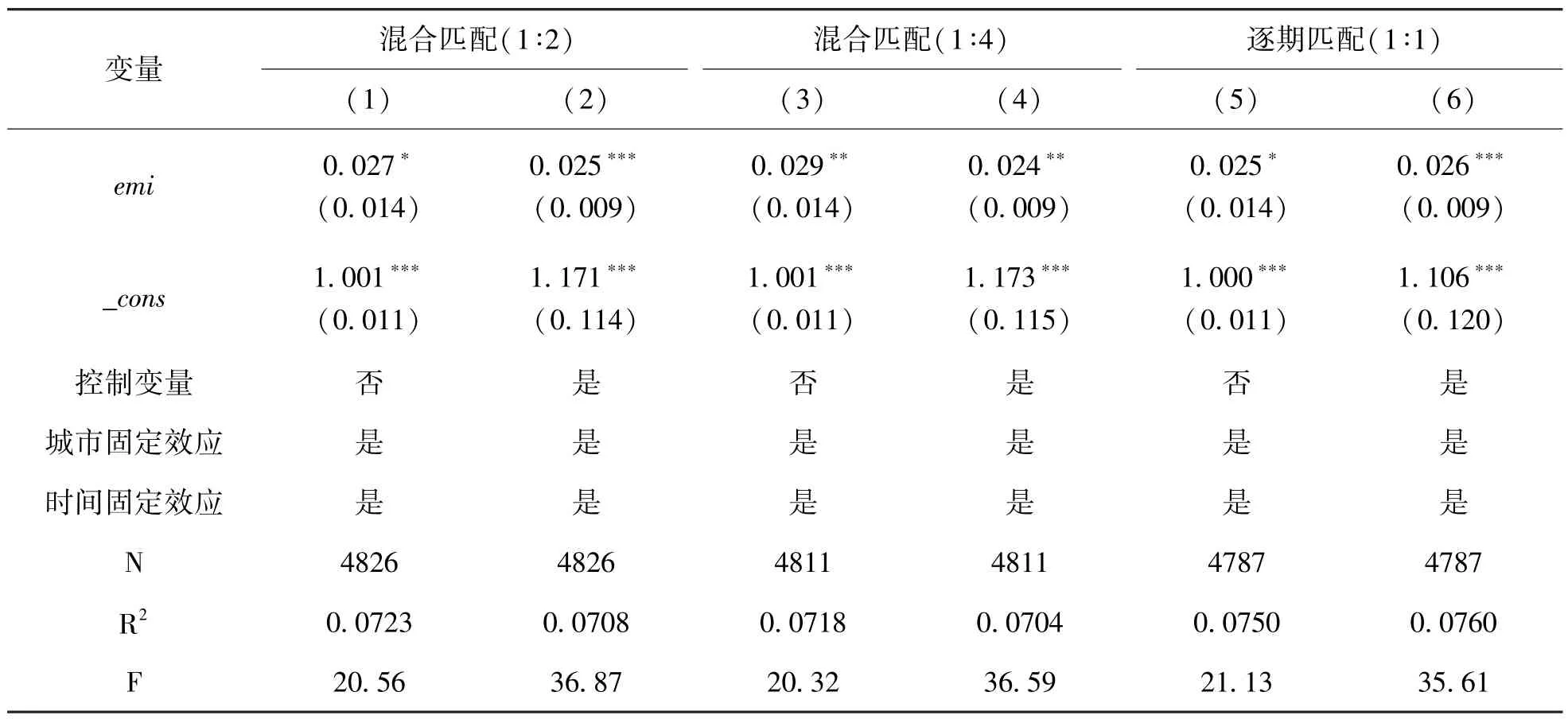
表4 PSM－DID 回歸結果

（3） 剔除其他政策的干擾

試點地區生態效率的提升可能是多個政策共同作用的結果，為了排除這種可能性，準確識別CETP 對生態效率的影響，需要剔除其他政策的干擾。結合相關文獻，2010 年及2014 年分別進行的低碳試點城市試點政策顯著促進了試點地區的綠色全要素生產率［27］，2008 年和2013 年在我國各地區實行的環境信息披露制度也能顯著促進生態效率增長［28］。參考曹清峰（2020）［29］的研究，在式（1） 的基礎上，估計以下方程：

其中，DID1 為環境信息披露制度虛擬變量矩陣，DID2 為低碳試點政策虛擬變量矩陣。其他變量同式（1）。表5 報告了回歸結果，可以發現，在加入這些政策一起回歸之后，核心解釋變量emi的系數仍顯著為正，且與PSM－DID 模型的系數相差較小，CETP 對地區生態效率還是有顯著的正向效應。因此，實證結論穩健。

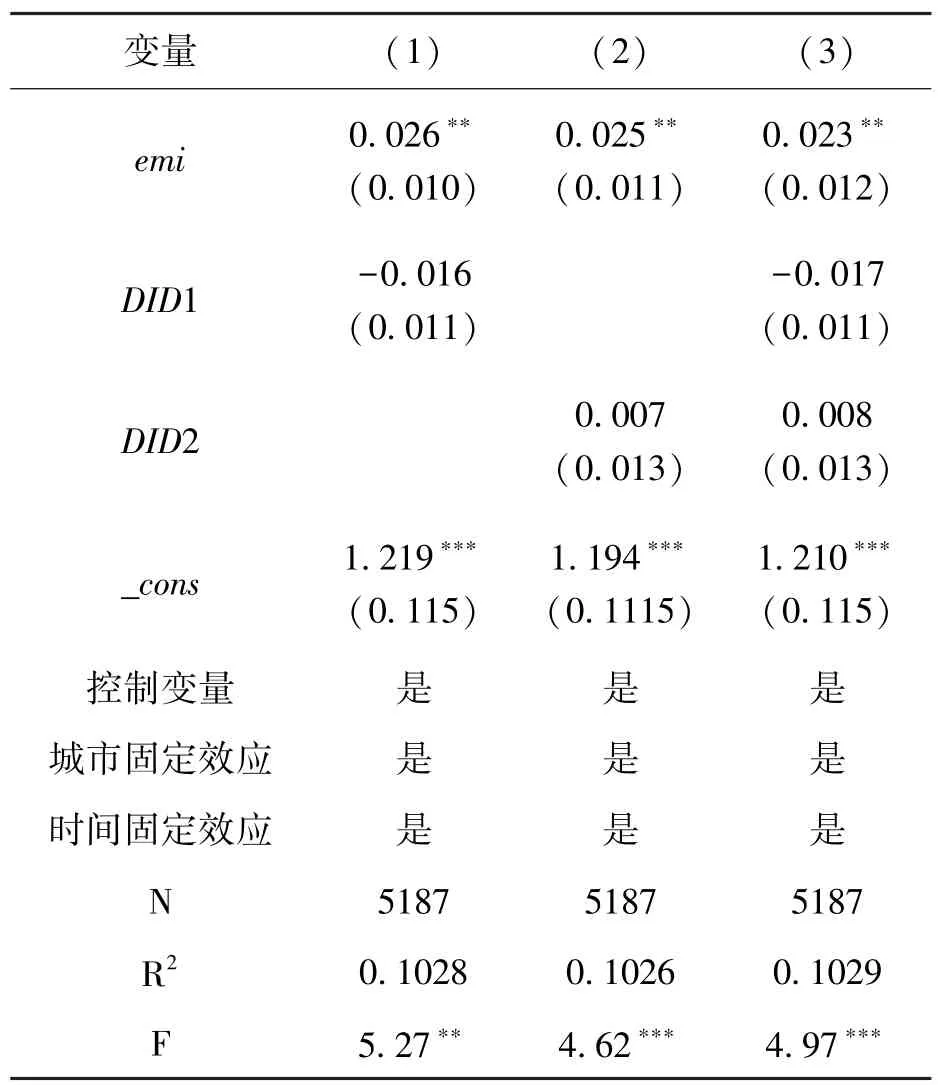
表5 排除其他政策干擾的回歸結果

6 間接效應及空間溢出效應分析

6.1 間接效應分析

上述基準回歸和穩健性檢驗結果均表明CETP顯著提高了城市綠色發展，接下來，使用中介效應模型對間接效應進行檢驗，結果如表6 所示。當中介變量為產業結構升級指數（ind）時，模型（1）的核心解釋變量emi的系數θ顯著為負，但模型（2） 中介變量（ind）的系數a不顯著，則需要進行Bootstrap 檢驗。有放回地進行1000 次重復抽樣后，結果得到的置信度為95%的置信區間包含0（［－0.001，0.001］），說明間接效應不顯著，即CETP 對生態效率的提升并不通過產業結構升級實現。產業結構升級的間接效應不存在，有可能是因為碳排放權交易利用市場機制來引導企業調整戰略、實現轉型并最終實現全社會產業鏈轉型升級和產業結構布局調整是一個長期的過程，需要較長的時間才能發揮效果，因此目前還不顯著。

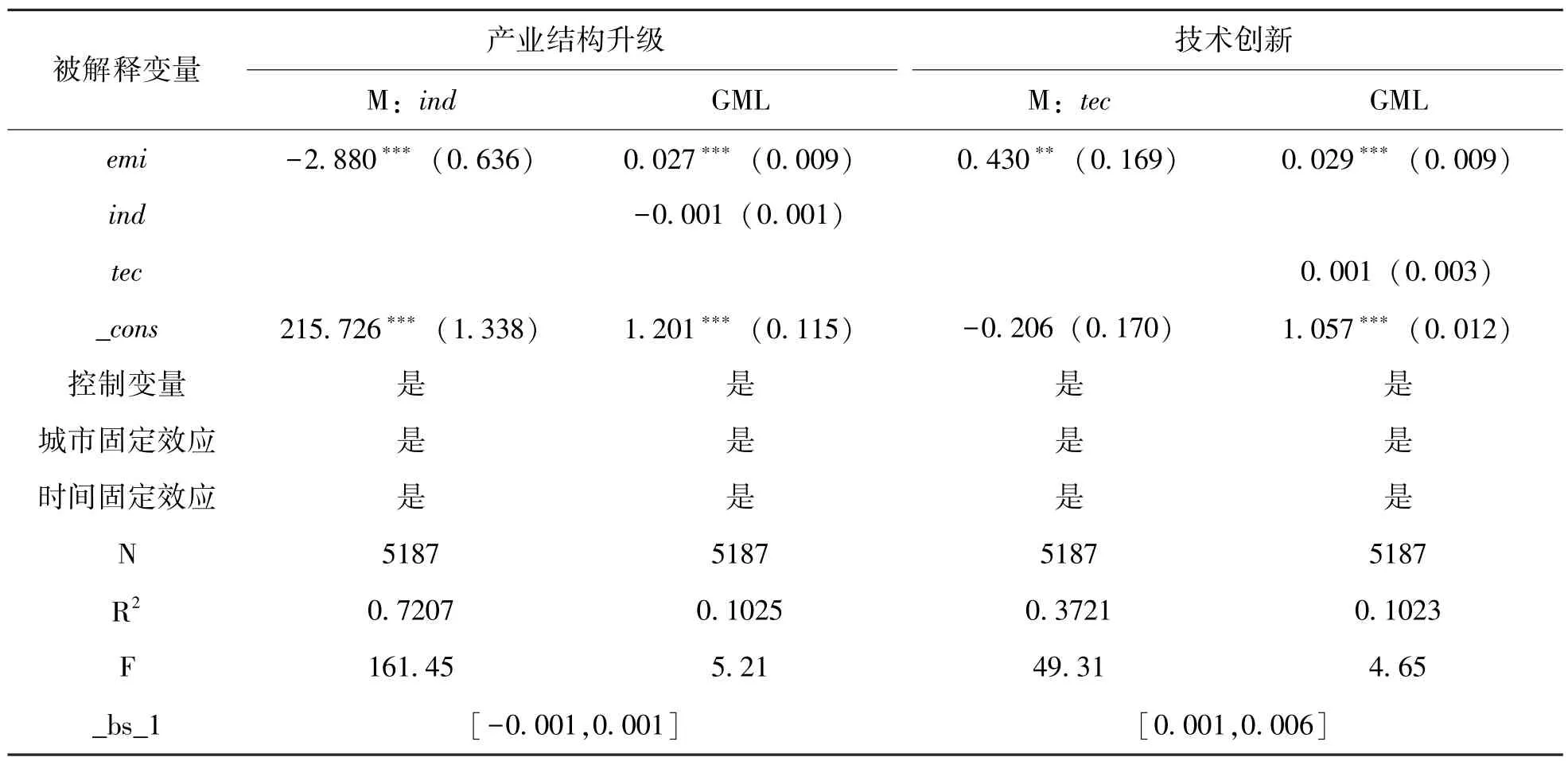
表6 間接效應分析

當中介變量為技術創新（tec）時，模型（3） 中emi的系數θ顯著為正，模型（4） 中介變量（ins）的系數a不顯著，進行1000 次Bootstrap 抽樣檢驗，發現95%的置信區間不包含0（［0.001，0.006］），表明間接效應顯著存在，繼續對比θ*a與b的符號，發現符號相同，則中介效應屬于部分間接效應，此時的效應量為θ*a/b＝1.48%。說明CETP產生的創新效應間接推動了綠色發展，效應量約為1.48%，部分驗證了假設2。

6.2 空間溢出效應分析

（1） 空間自相關檢驗及模型選擇

只有存在空間相關性，才能夠使用空間計量方法來進行模型的構建和估計。本文擬采用全局Moran's I 指數檢驗城市生態效率的全局空間相關性，運用Stata 16.0 軟件，測算2004 ～2021 年生態效率的全局Moran's I 指數，如表7 所示。可以看出，Moran's I 指數在大多數年份均為正，且在5%的水平上顯著，說明地級市之間生態效率具有顯著的空間正相關性，因此使用空間計量模型來研究生態效率是有必要的。

表7 生態效率的Moran's I 指數

本文綜合利用LM 檢驗、Wald 檢驗和LR 檢驗來對空間模型的選擇進行判斷，檢驗結果如表8所示。結果顯示，LMlag、LMerror 和穩健的LMlag、LMerror 均在1%的顯著性水平下顯著，分別拒絕了沒有空間滯后被解釋變量的原假設和沒有空間自相關誤差項的原假設，因此使用SDM 模型能更好的擬合本文的數據。Wald 檢驗和LR 檢驗的結果均在1%的顯著性水平下顯著，分別拒絕了SDM模型能簡化為SAR 模型和SDM 模型能簡化為SEM模型的原假設，所以最終本文選擇基于空間SDM模型的SDID 模型進行實證。

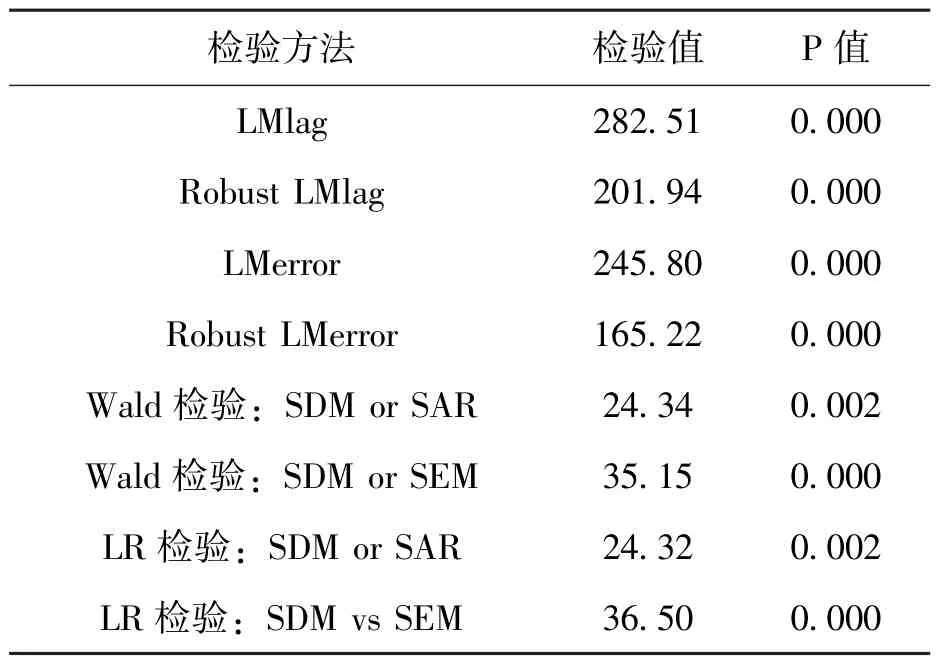
表8 模型設定檢驗

（2） 空間溢出效應分析

使用SDM－DID 模型進行回歸，估計結果見表9 的模型（1） ～（2）。模型（1） 是有約束的SDM－DID 模型回歸結果，模型（2） 是無約束的SDM－DID 模型回歸結果。具體來看，在試點地區，碳排放權交易政策的影響為0.126，比PSM－DID模型的效應（0.026）大。同時，列（1） 中，WD的系數顯著為負，碳排放權交易試點對周邊地區產生了顯著的負向溢出效應，說明其“污染避難所效應” 和“虹吸效應” 作用比“溢出效應” 更強，驗證了假設3。就效應分解來看，列（2） 中，WT，TD的系數為－0.364，為負數，說明碳排放權交易政策的實施對周邊試點城市產生了顯著的負向溢出效應。WNT，TD的系數為負，但接近于0且不顯著，說明政策對鄰近的非試點城市有負面影響，但不顯著。

（3） 空間穩健性檢驗

本文使用鄰接矩陣和經濟距離矩陣來檢驗空間計量實證結果的穩健性。結果見表9 的模型（3）～（6）。可以看出，替換權重矩陣后，模型（3）～（6）中核心解釋變量emi的系數依然顯著為正，與前文一致，且WT，TD和WNT，TD的符號與顯著性也與前面的實證結果一致，雖然經濟距離矩陣的WD符號不顯著，但可能是由于在權重矩陣中加入了經濟因素，對城市之間距離的刻畫有些失真，但并不影響最終的實證結果，穩健性檢驗通過。

7 結論與啟示

本文以2003～2021 年全國273 個城市的面板數據為例，通過PSM－DID 模型和SDID 模型，討論了碳排放權交易試點（CETP）影響綠色發展的理論機制，并研究了CETP 對綠色發展的空間效應，研究結果表明： （1） 無論是使用傳統DID 模型還是PSM－DID 模型，結果都顯示CETP 能夠促進試點地區綠色發展，并且通過了安慰劑檢驗； （2）調整PSM 近鄰匹配比例為1 ∶2、1 ∶4 和使用逐期匹配法后，結論依舊穩健； （3） 剔除了低碳城市試點政策和環境信息披露制度的干擾后，CETP依然能夠顯著促進地區綠色發展； （4） 中介效應檢驗發現“產業結構效應” 不顯著，但“創新效應” 顯著，即CETP 產生的創新效應推動了生態效率的提升； （5） CETP 對周邊地區產生了顯著的負向溢出效應，就效應分解來看，CETP 的實施對周邊試點城市產生了顯著負向的溢出效應，但對非試點城市的生態效率無明顯影響，而且替換空間權重矩陣后結果依然穩健。

通過本文理論和實證研究，得到以下建議：（1） 促進全國碳排放權交易市場健康發展。鑒于CETP 在提高試點地區綠色發展水平方面的有效性，應加強碳排放權交易市場的主導作用，盡可能減少勾連和投機等各種可能阻礙碳排放權交易市場效率的不正當交易行為； 另外，應完善碳排放權交易市場機制設計，提高交易的有效性； （2）充分利用碳排放權交易的創新效應。可以適度提高環保企業的碳排放配額，以激勵企業增加技術投資，促進低碳技術的研發； 降低污染企業的碳配額，加快該類型企業的技術轉型和創新，從而實現綠色發展； （3） 加強碳排放權交易的省際合作。積極推廣成功地區的試點經驗，建立碳排放權交易市場區域合作治理體系，并利用鄰近地區的互補優勢，進一步實現碳排放權交易市場的協調發展。

注釋：

①地理距離權重矩陣： 其空間權重矩陣元素設定為兩城市地理中心之間的直線距離的反函數。

②鄰接矩陣： 如果兩地區空間相鄰，則空間權重矩陣元素記為1，否則為0。

③經濟地理距離權重矩陣： 基于城市間的地理距離和人均GDP設定的權重矩陣。

④版面所限，結果留存備索。