基于壓氣機(jī)三維徹體力模型的葉尖射流擴(kuò)穩(wěn)方法

楊陽(yáng), 郭政波

(中國(guó)飛行試驗(yàn)研究院發(fā)動(dòng)機(jī)所, 西安 710089)

航空發(fā)動(dòng)機(jī)壓縮系統(tǒng)的氣動(dòng)穩(wěn)定性一直是中外先進(jìn)航空發(fā)動(dòng)機(jī)研究的重點(diǎn)[1-2]。由于壓氣機(jī)氣動(dòng)失穩(wěn)會(huì)帶來(lái)嚴(yán)重后果,設(shè)計(jì)者在設(shè)計(jì)階段即預(yù)留足夠的穩(wěn)定裕度,并嘗試采用多種擴(kuò)穩(wěn)方法擴(kuò)大壓氣機(jī)穩(wěn)定工作范圍[3]。目前,一般來(lái)說(shuō),獲得壓氣機(jī)穩(wěn)定工作邊界是靠部件試驗(yàn)的方法或采用全環(huán)非定常RANS(Reynolds averaged Navier-Stokes equations)方法[4-5]進(jìn)行數(shù)值模擬,但是試驗(yàn)方法需要耗費(fèi)大量的人力、物力、財(cái)力,而且試驗(yàn)方法往往都是在壓氣機(jī)設(shè)計(jì)完成后才可進(jìn)行。因此在壓氣機(jī)設(shè)計(jì)階段,研究人員希望研究出能夠?qū)Πl(fā)動(dòng)機(jī)的穩(wěn)定邊界進(jìn)行預(yù)測(cè)的穩(wěn)定性預(yù)測(cè)模型,并能夠?qū)U(kuò)穩(wěn)措施等引起壓氣機(jī)穩(wěn)定邊界變化的情況進(jìn)行模擬。

對(duì)壓氣機(jī)的全環(huán)非定常RANS方法精度主要依賴于湍流模型的準(zhǔn)確性和計(jì)算網(wǎng)格的質(zhì)量及數(shù)量,然而針對(duì)多級(jí)壓氣機(jī)三維黏性流動(dòng)仿真這類工程問(wèn)題,其所需的巨大計(jì)算網(wǎng)格量使其目前仍不能被工程設(shè)計(jì)所接受。三維徹體力模型是目前普遍認(rèn)可的分析多級(jí)軸流壓氣機(jī)在大尺度復(fù)雜進(jìn)氣畸變下氣動(dòng)性能及穩(wěn)定性的計(jì)算工具,其能夠在保證必要的工程計(jì)算精度要求的同時(shí),大幅降低對(duì)計(jì)算資源的消耗。Hale等[6-8]研究了基于非定常歐拉方程的全三維無(wú)黏壓氣機(jī)穩(wěn)定性分析計(jì)算方法,采用徹體力方法并結(jié)合穩(wěn)定性經(jīng)驗(yàn)參數(shù)判據(jù)建立了三維穩(wěn)定性模型TEACC(turbine engine analysis compressor code)。該方法中源項(xiàng)采用流線曲率法計(jì)算,控制方程為Euler方程。采用該模型具有很高的計(jì)算效率。Davis等[9]采用該模型對(duì)單轉(zhuǎn)子和多級(jí)壓氣機(jī)下的畸變進(jìn)氣均取得了較好的預(yù)測(cè)效果。Gong等[10]也基于徹體力方法建立了三維穩(wěn)定性模型,源項(xiàng)采用壓氣機(jī)特性計(jì)算得到,并將壓氣機(jī)過(guò)失速的特性采用拋物線方程代替。

壓氣機(jī)的葉尖位置流動(dòng)特性對(duì)壓氣機(jī)氣動(dòng)穩(wěn)定性有重要影響,高國(guó)榮等[11]以某大涵道比渦扇發(fā)動(dòng)機(jī)的十級(jí)高壓壓氣機(jī)為研究對(duì)象,在高轉(zhuǎn)速壓氣機(jī)試驗(yàn)器上試驗(yàn)研究了葉尖間隙對(duì)壓氣機(jī)非設(shè)計(jì)轉(zhuǎn)速性能特性于穩(wěn)定邊界的影響。表明間隙對(duì)氣動(dòng)穩(wěn)定性有顯著影響,且影響主要集中在葉高80%截面以上,使得壓氣機(jī)更容易進(jìn)入失速狀態(tài)。曹傳軍等[12]以某民用大涵道比渦扇發(fā)動(dòng)機(jī)高壓壓氣機(jī)進(jìn)口級(jí)為研究對(duì)象,通過(guò)數(shù)值方法分析了葉尖間隙對(duì)進(jìn)口級(jí)高負(fù)荷跨音速轉(zhuǎn)子葉片氣動(dòng)性能的影響。結(jié)果表明葉尖泄漏流與通道激波相互作用,泄漏流穿過(guò)激波后在葉片壓力面?zhèn)刃纬奢^大的高熵值損失區(qū)域,何成等[13]對(duì)不同工況下葉尖間隙流動(dòng)的特點(diǎn)進(jìn)行了分析,討論了壓氣機(jī)轉(zhuǎn)子葉頂兩個(gè)低速區(qū)的形成機(jī)理,以及該轉(zhuǎn)子在多種換算轉(zhuǎn)速下的失速機(jī)制。研究表明,轉(zhuǎn)子失速是近壓力面前緣和吸力面尾緣兩個(gè)低速堵塞區(qū)共同作用的結(jié)果。陳歡歡等[14]為研究葉尖間隙對(duì)級(jí)環(huán)境下壓氣機(jī)氣動(dòng)性能的影響,以帶導(dǎo)葉的超音壓氣機(jī)級(jí)為研究對(duì)象進(jìn)行三維數(shù)值計(jì)算。結(jié)果表明:隨著葉尖間隙的增大,轉(zhuǎn)子葉尖處激波向上游移動(dòng),靜子進(jìn)口氣流攻角增大,最終導(dǎo)致壓氣機(jī)穩(wěn)定工作裕度、轉(zhuǎn)子峰值點(diǎn)效率和靜子低損失范圍降低。以上研究結(jié)果都表明葉尖處的高熵值流動(dòng)是壓氣機(jī)失速的重要原因。由此引出了葉尖射流擴(kuò)穩(wěn)技術(shù)研究,該研究方向是近十幾年國(guó)內(nèi)外研究的重點(diǎn)。Gabriele等[15]以單級(jí)低速軸流壓氣機(jī)轉(zhuǎn)子為對(duì)象開(kāi)展了葉尖噴射的數(shù)值模擬研究,發(fā)現(xiàn)分散式射流比全環(huán)向射流擴(kuò)穩(wěn)效果更好。Kefalakis等[16]在一臺(tái)高速單級(jí)軸流壓氣機(jī)上研究了葉尖噴射對(duì)壓氣機(jī)葉尖流場(chǎng)的影響,發(fā)現(xiàn)穩(wěn)定裕度的提高量與噴射流動(dòng)量和自由來(lái)流動(dòng)量的比值有密切關(guān)系。Suder等[17]在跨聲速壓氣機(jī)上100%設(shè)計(jì)轉(zhuǎn)速下采用2%的主流流量,使穩(wěn)定邊界左移6%,而在70%轉(zhuǎn)速下采用1%的主流流量使穩(wěn)定邊界左移了30%。Suder等[17]認(rèn)為射流能夠擴(kuò)穩(wěn)的原因是速度較高的葉尖射流會(huì)降低葉尖的攻角和載荷,則對(duì)于葉尖觸發(fā)失穩(wěn)的壓氣機(jī)可以繼續(xù)節(jié)流,從而壓氣機(jī)能夠在更低的流量下穩(wěn)定工作,并認(rèn)為射流擴(kuò)穩(wěn)的效果與葉尖的平均軸向速度有直接關(guān)系。影響葉尖射流擴(kuò)穩(wěn)效果的有射流流量、射流孔數(shù)目、射流孔的周向分布以及射流角度等。目前,研究者對(duì)射流流量對(duì)擴(kuò)穩(wěn)效果的影響認(rèn)識(shí)是一致的,但對(duì)于其他幾個(gè)影響因素的認(rèn)識(shí)還不夠充分。

在前人在壓氣機(jī)徹體力模型和葉尖射流擴(kuò)穩(wěn)研究的基礎(chǔ)上,現(xiàn)開(kāi)展基于壓氣機(jī)三維黏性徹體力模型的葉尖射流擴(kuò)穩(wěn)技術(shù)研究,首先以Stage 35單級(jí)軸流壓氣機(jī)為研究對(duì)象,以試驗(yàn)數(shù)據(jù)驗(yàn)證三維徹體力模型對(duì)壓氣機(jī)特性和端壁處流動(dòng)的準(zhǔn)確模擬。以多級(jí)軸流壓氣機(jī)為研究對(duì)象,建立多級(jí)壓氣機(jī)的三維徹體力模型,研究葉尖射流對(duì)多級(jí)壓氣機(jī)的擴(kuò)穩(wěn)效果。在建模過(guò)程中,利用ANSYS CFX 提供的源項(xiàng)接口,將動(dòng)量源項(xiàng)和能量源項(xiàng)添加至CFX迭代過(guò)程中,實(shí)現(xiàn)了壓氣機(jī)全通道計(jì)算,由于其求解的方程為N-S方程(Navier-Stokes equations),因此,對(duì)壓氣機(jī)端壁處的流動(dòng)也能準(zhǔn)確模擬。

1 壓氣機(jī)徹體力模型建立方法

1.1 控制方程

壓氣機(jī)內(nèi)部三維黏性流動(dòng)的控制方程為N-S方程,在直角坐標(biāo)系下,不考慮重力以及與外界換熱,帶源項(xiàng)的N-S方程如下。

(1)流量方程:

(1)

(2)動(dòng)量方程:

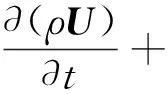
(2)

(3)能量方程:

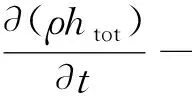
(3)

(4)

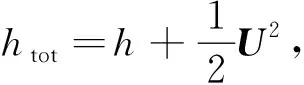
1.2 源項(xiàng)獲取方法

建立徹體力模型的關(guān)鍵是獲得不同工況下的葉片動(dòng)量源項(xiàng)與能量源項(xiàng),采用文獻(xiàn)[10]提出的源項(xiàng)計(jì)算方法。將葉片對(duì)氣流的力分為垂直于流動(dòng)的升力和與流動(dòng)方向相反的阻力。葉片周向力和阻力的計(jì)算公式為

(5)

(6)

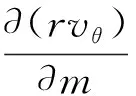
由式(5)和式(6)可見(jiàn),求體積力的關(guān)鍵是獲得葉片排的環(huán)量增加量和熵值增加量。通過(guò)ANSYS CFX計(jì)算單通道壓氣機(jī)級(jí)在不同轉(zhuǎn)速下的整個(gè)工作壓比范圍內(nèi)的一系列工況點(diǎn),建立每個(gè)工況下的葉片排各個(gè)徑向位置的環(huán)量增加量和熵值增加量與該徑向位置對(duì)應(yīng)的進(jìn)口處的單位面積換算流量和換算轉(zhuǎn)速的關(guān)系數(shù)據(jù)庫(kù)。在徹體力模型計(jì)算過(guò)程中,根據(jù)相似原理,以葉片排處計(jì)算點(diǎn)的徑向位置以及其對(duì)應(yīng)的進(jìn)口處的單位面積換算流量和換算轉(zhuǎn)速對(duì)提取的環(huán)量增加量和熵值增加量插值,得到當(dāng)前工作點(diǎn)當(dāng)前葉片排位置的每個(gè)網(wǎng)格節(jié)點(diǎn)的源項(xiàng)。插值過(guò)程由FORTRAN程序?qū)崿F(xiàn),該程序通過(guò)ANSYS CFX求解器提供的源項(xiàng)接口,將能量源項(xiàng)和動(dòng)量源項(xiàng)實(shí)時(shí)返回至N-S方程的求解過(guò)程中,從而實(shí)現(xiàn)無(wú)葉片條件下的三維黏性計(jì)算。

2 模型驗(yàn)證

以NASA Lewis研究中心設(shè)計(jì)的低展弦比跨聲速單級(jí)壓氣機(jī)Stage 35作為研究算例,Stage 35是核心壓氣機(jī)的進(jìn)口級(jí),有公開(kāi)的幾何參數(shù)、實(shí)驗(yàn)結(jié)果和特性參數(shù)[18]。以Stage35作為研究對(duì)象,既可以考核本文研究的模型的通用性,同時(shí)通過(guò)試驗(yàn)數(shù)據(jù)對(duì)模型進(jìn)行驗(yàn)證。

首先對(duì)Stage 35進(jìn)行100%、90%、80%、70%設(shè)計(jì)轉(zhuǎn)速等4個(gè)轉(zhuǎn)速下從堵塞狀態(tài)到失穩(wěn)邊界的單通道定常RANS計(jì)算,獲得了各狀態(tài)下的“環(huán)量項(xiàng)”與“熵增項(xiàng)”。

利用壓氣機(jī)三維黏性徹體力模型計(jì)算壓氣機(jī)流場(chǎng)和特性時(shí),計(jì)算域?yàn)闊o(wú)葉片的環(huán)形通道。對(duì)于葉片排的處理方法是,將轉(zhuǎn)子葉片的前緣線、尾緣線繞壓氣機(jī)軸旋轉(zhuǎn)得到2個(gè)面,這2個(gè)面與機(jī)匣和輪轂形成轉(zhuǎn)子的作用區(qū)域,源項(xiàng)將作用在該域內(nèi)所有網(wǎng)格節(jié)點(diǎn)上。由于計(jì)算域內(nèi)不存在葉片,故網(wǎng)格量大大減少,實(shí)際計(jì)算量減少兩個(gè)數(shù)量級(jí)。利用壓氣機(jī)三維黏性徹體力模型計(jì)算了Stage35在均勻進(jìn)氣條件下,100%設(shè)計(jì)轉(zhuǎn)速和90%設(shè)計(jì)轉(zhuǎn)速的總壓比特性,并與實(shí)驗(yàn)值進(jìn)行了對(duì)比,如圖1所示,計(jì)算過(guò)程中以數(shù)值發(fā)散作為失穩(wěn)邊界。

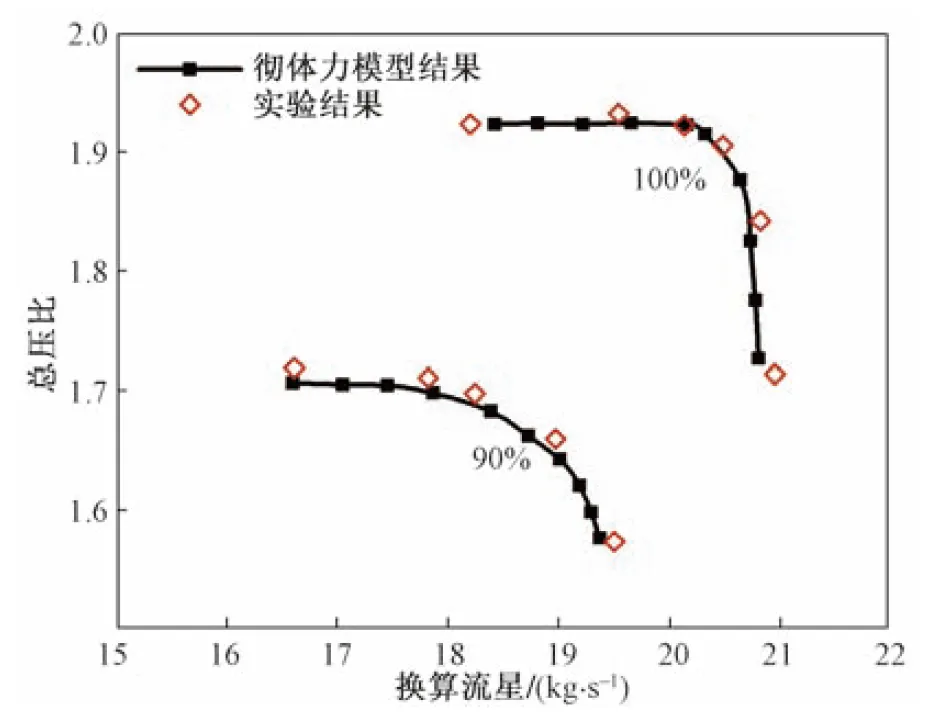
圖1 Stage35徹體力模型計(jì)算的總壓比特性及與試驗(yàn)數(shù)據(jù)的對(duì)比Fig.1 Characteristics of total pressure ratio calculated by Stage35 bulk body force model and comparison with test data

由圖1可以看出,徹體力模型計(jì)算結(jié)果與試驗(yàn)值非常吻合,總壓比特性線趨勢(shì)和絕對(duì)值均與實(shí)驗(yàn)結(jié)果相符,最大誤差不超過(guò)0.8%;對(duì)于失穩(wěn)點(diǎn)流量,模型判斷結(jié)果比實(shí)驗(yàn)結(jié)果要大1.2%,這是模型判斷失穩(wěn)的準(zhǔn)則過(guò)于保守所致。

圖2和圖3給出了徹體力模型計(jì)算的近設(shè)計(jì)點(diǎn)的擴(kuò)散因子和總溫比特性徑向分布與實(shí)驗(yàn)數(shù)據(jù)的對(duì)比。其中擴(kuò)散因子定義為

(7)

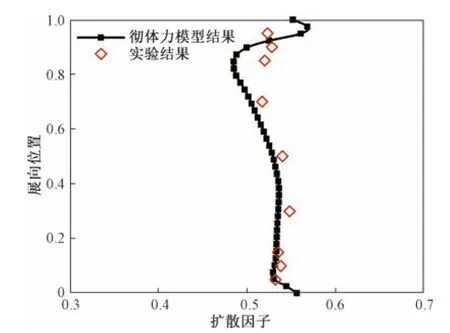
圖2 Stage35徹體力模型計(jì)算的近設(shè)計(jì)點(diǎn)轉(zhuǎn)子擴(kuò)散因子展向分布Fig.2 The spread distribution of the diffusion factor near the design point calculated by the thorough force model of Stage35

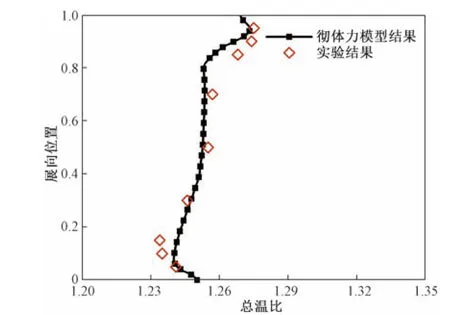
圖3 Stage35徹體力模型計(jì)算的近設(shè)計(jì)點(diǎn)轉(zhuǎn)子總溫比的展向分布Fig.3 The spread distribution of the total temperature ratio of the rotor near the design point calculated by the Stage35 bulk body force model

式(7)中:V′LE為葉柵前緣相對(duì)速度;V′TE為葉柵尾緣相對(duì)速度;ΔV′θ為周向相對(duì)速度在葉柵前后的變化量,這幾個(gè)氣動(dòng)參數(shù)都是周向質(zhì)量平均的結(jié)果;τ為葉柵稠度。

由圖2可見(jiàn),轉(zhuǎn)子的擴(kuò)散因子值與試驗(yàn)值吻合較好,只是在80%葉高以上有一定差異,但趨勢(shì)基本一致。圖3中總溫比特性與試驗(yàn)值吻合較好。這些結(jié)果表明模型計(jì)算能夠捕捉到流場(chǎng)細(xì)節(jié),同時(shí)能較好地模擬端壁流動(dòng)。

3 葉尖射流擴(kuò)穩(wěn)

3.1 多級(jí)壓氣機(jī)流場(chǎng)與性能計(jì)算分析

基于三維黏性徹體力模型計(jì)算了某渦扇發(fā)動(dòng)機(jī)的高壓壓氣機(jī)的前三級(jí),帶導(dǎo)流葉片共七排葉片。先分別以各級(jí)為研究對(duì)象,進(jìn)行各級(jí)的單通道定常RANS計(jì)算。在徹體力模型計(jì)算時(shí),以各級(jí)進(jìn)口單位面積換算流量和換算轉(zhuǎn)速作為各級(jí)葉排的插值自變量。根據(jù)相似原理,與單級(jí)徹體力模型計(jì)算網(wǎng)格劃分辦法類似,將各排葉片的前緣線、尾緣線繞壓氣機(jī)形成的面與機(jī)匣、輪轂圍成的區(qū)域作為該葉片的計(jì)算域。在該計(jì)算域內(nèi)添加葉排的源項(xiàng)。圖4為徹體力模型計(jì)算的多級(jí)壓氣機(jī)在90%和100%轉(zhuǎn)速下的總壓比特性。在圖4中標(biāo)注了90%轉(zhuǎn)速下的A、B兩個(gè)工作點(diǎn),其中A點(diǎn)是穩(wěn)定工作邊界點(diǎn),B點(diǎn)為穩(wěn)定工作點(diǎn)。圖5～圖8分別給出A點(diǎn)和B點(diǎn)的軸向速度和靜熵在子午面和第三級(jí)轉(zhuǎn)子出口截面的分布。可以看到,兩個(gè)狀態(tài)點(diǎn)的流場(chǎng)參數(shù)分布的區(qū)別主要在第三級(jí)轉(zhuǎn)子葉尖處。A工況下,第三級(jí)轉(zhuǎn)子葉尖處軸向速度較小,同時(shí)熵值較大,說(shuō)明在穩(wěn)定邊界點(diǎn),葉尖流動(dòng)的阻塞效應(yīng)較為嚴(yán)重。因此,可以認(rèn)為,壓氣機(jī)的失穩(wěn)很有可能是因?yàn)樵撎幍淖枞鸬摹＿M(jìn)一步表明本文建立的模型能夠較準(zhǔn)確地模擬端壁流動(dòng)。

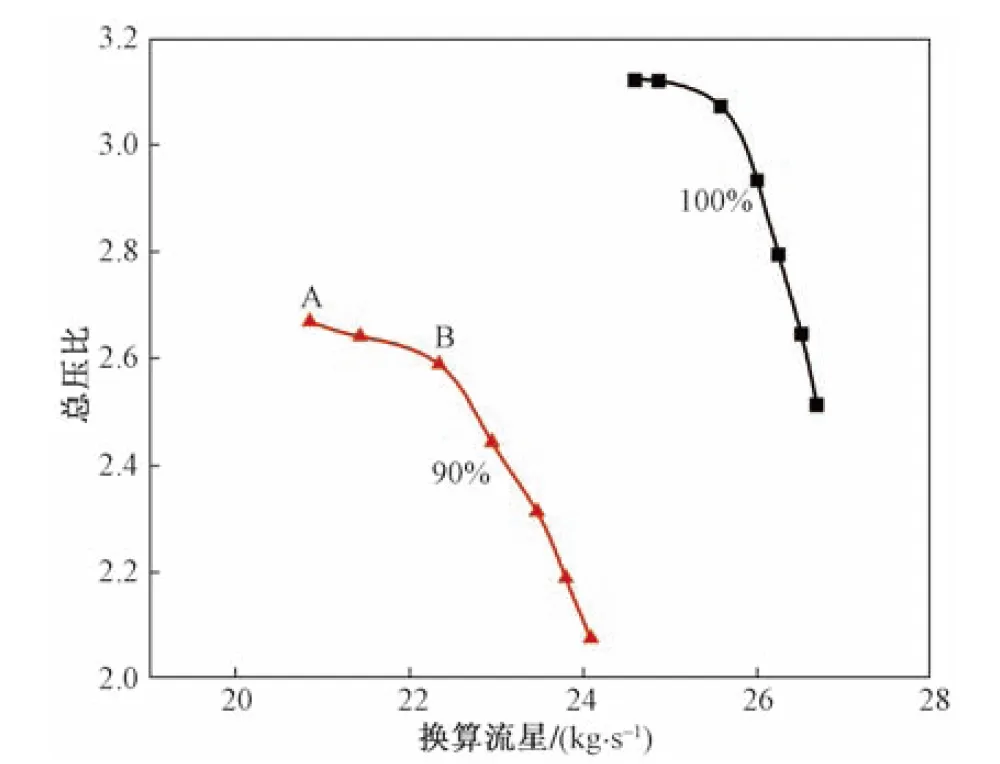
圖4 某多級(jí)壓氣機(jī)徹體力模型計(jì)算的總壓比特性Fig.4 Characteristics of total pressure ratio calculated by a multistage compressor bulk body force model

圖5 B工況子午面的軸向速度分布Fig.5 The axial velocity distribution of the meridional plane at Point B

圖6 A工況子午面的軸向速度分布Fig.6 The axial velocity distribution of the meridional plane at Point A

圖7 B工況子午面的靜熵分布Fig.7 The static entropy distribution of the meridional plane at Point B

圖8 A工況子午面的靜熵分布Fig.8 The static entropy distribution of the meridional plane at Point A

3.2 壓氣機(jī)葉尖射流擴(kuò)穩(wěn)數(shù)值計(jì)算分析

圖9所示為上文計(jì)算的多級(jí)壓氣機(jī)近失穩(wěn)點(diǎn)的各級(jí)轉(zhuǎn)子的擴(kuò)散因子徑向分布。由圖9可以看到,在該狀態(tài)點(diǎn),在第三級(jí)轉(zhuǎn)子的80%葉高以上擴(kuò)散因子都在0.6以上,并遠(yuǎn)大于第一級(jí)和第二級(jí)轉(zhuǎn)子在該位置的擴(kuò)散因子值,由于求得該擴(kuò)散因子的氣動(dòng)參數(shù)都是周向平均得到的結(jié)果,而擴(kuò)散因子反映的是轉(zhuǎn)子葉片排周向平均損失的大小,也反映了氣流的平均阻塞大小,所以可以認(rèn)為第三級(jí)轉(zhuǎn)子葉尖處是最易發(fā)生堵塞以致壓氣機(jī)失穩(wěn)的部位。這與圖5～圖8所示是一致的。因此,此將射流位置選擇在第三級(jí)轉(zhuǎn)子之前的機(jī)匣位置處。射流孔數(shù)目為12個(gè),在周向均勻分布,即每隔30°布置一個(gè)射流孔,射流流量約為設(shè)計(jì)點(diǎn)流量的4.6%,射流角度為沿軸向。

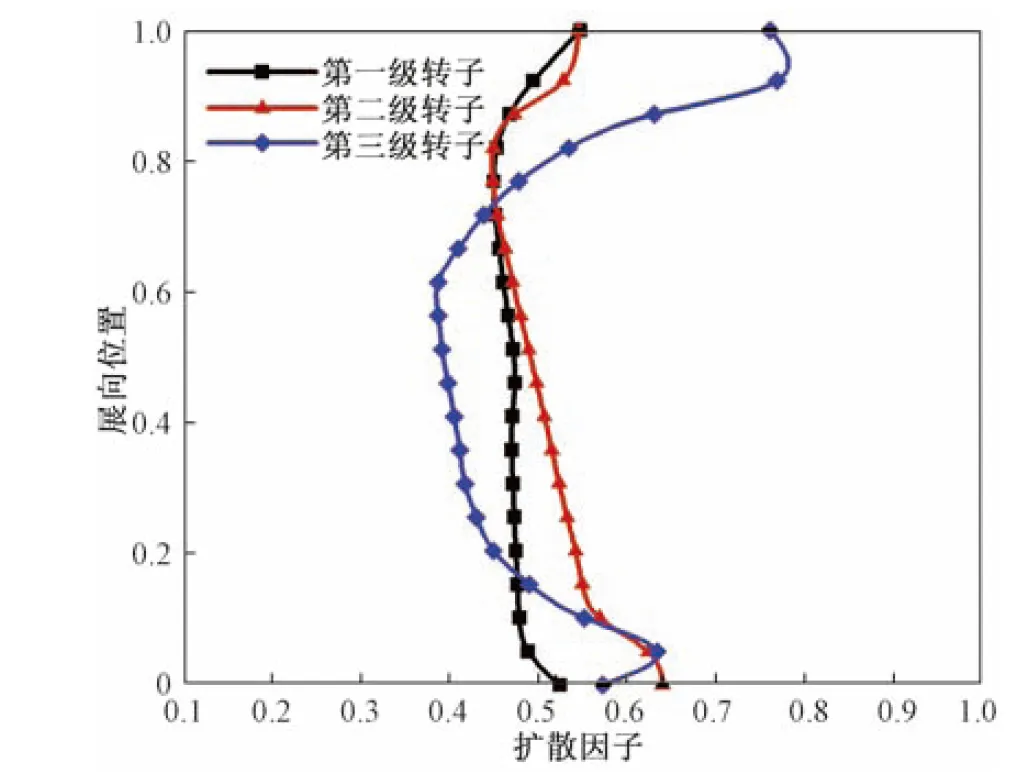
圖9 各級(jí)轉(zhuǎn)子擴(kuò)散因子的展向分布Fig.9 The spread distribution of diffusion factors in different rotors

使用壓氣機(jī)三維黏性徹體力模型計(jì)算了均勻進(jìn)氣時(shí)多級(jí)壓氣機(jī)的第三級(jí)轉(zhuǎn)子葉尖射流的擴(kuò)穩(wěn)效果。圖10所示為有無(wú)射流作用時(shí)的壓氣機(jī)總壓比特性。可以看到,在射流作用下,壓氣機(jī)失穩(wěn)點(diǎn)明顯向左移動(dòng),說(shuō)明葉尖射流具有擴(kuò)穩(wěn)的效果,也說(shuō)明本文三維黏性徹體力模型能夠準(zhǔn)確模擬擴(kuò)穩(wěn)對(duì)壓氣機(jī)性能的影響。

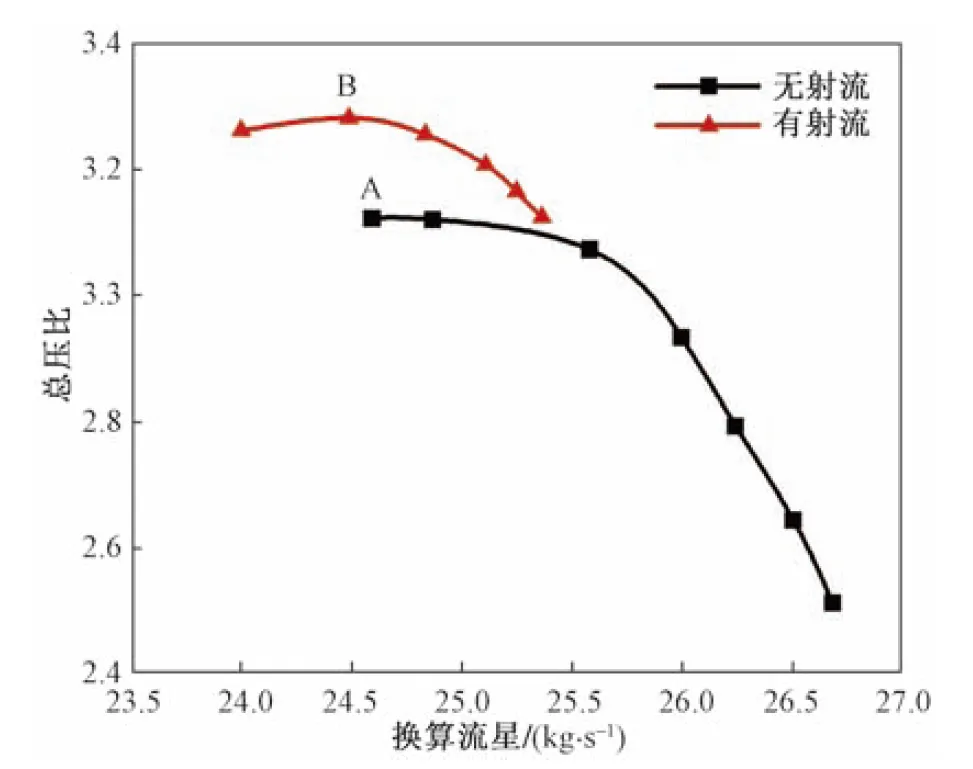
圖10 射流對(duì)壓氣機(jī)總壓比特性的影響Fig.10 Effect of jet flow on total pressure ratio of compressor

將穩(wěn)定裕度增加量定義為

(8)

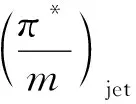
根據(jù)式(8),有射流的穩(wěn)定裕度增加量為7.06%。下面簡(jiǎn)單分析葉尖射流的擴(kuò)穩(wěn)機(jī)理。

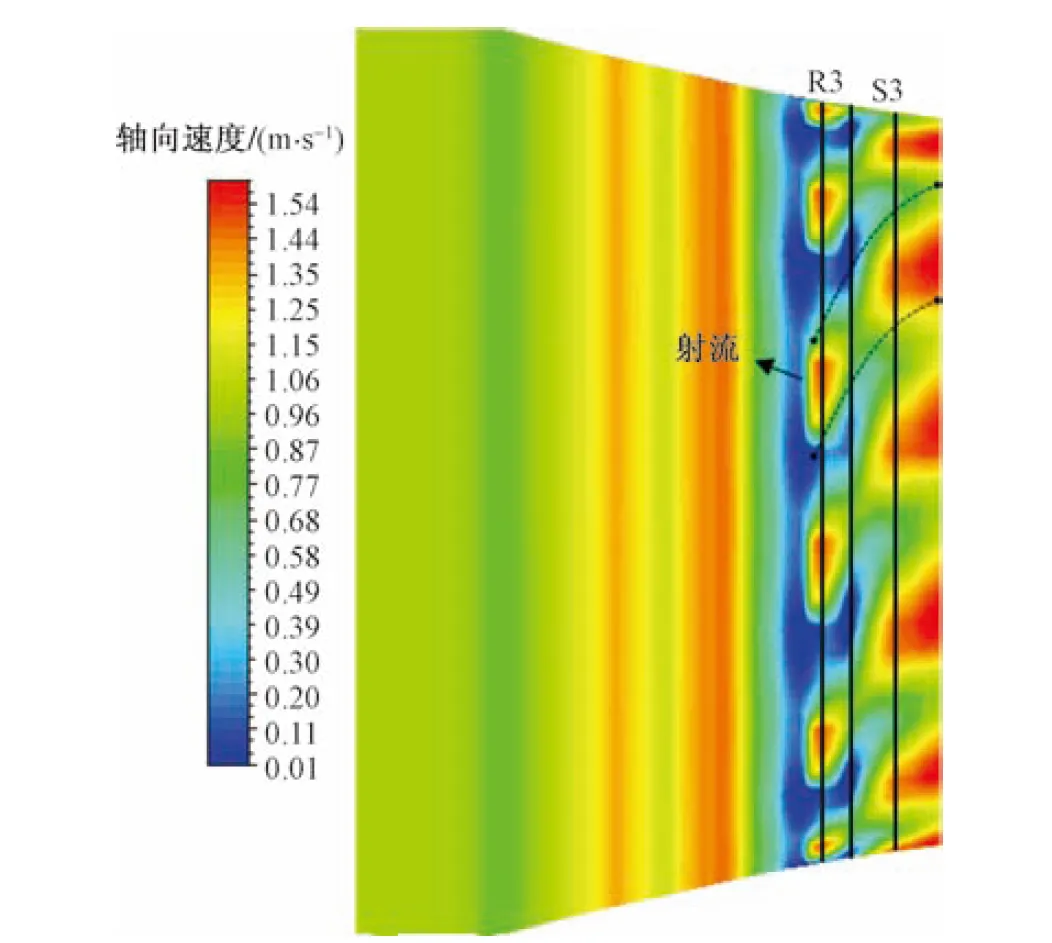
R3和S3分別指第三級(jí)轉(zhuǎn)子和第三級(jí)靜子計(jì)算域圖11 有射流時(shí)近失穩(wěn)點(diǎn)95%葉高處軸向速度的分布Fig.11 Distribution of axial velocity near instability point 95% at blade height with jet

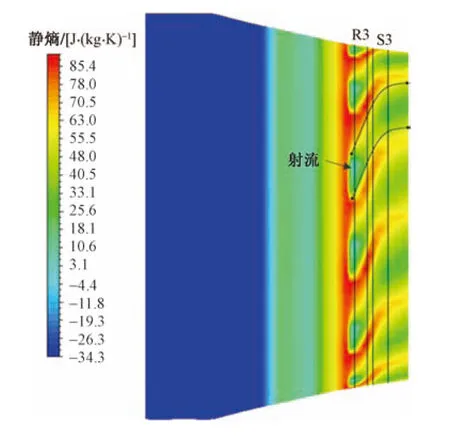
R3和S3分別指第三級(jí)轉(zhuǎn)子和第三級(jí)靜子計(jì)算域圖12 有射流時(shí)近失穩(wěn)點(diǎn)95%葉高處?kù)o熵的分布Fig.12 Static entropy distribution near the instability point at 95% blade height with jet

4 結(jié)論

本文研究的三維黏性徹體力模型對(duì)壓氣機(jī)內(nèi)部三維黏性流場(chǎng)模擬是準(zhǔn)確的,對(duì)于單級(jí)壓氣機(jī),計(jì)算的總壓比特性與實(shí)驗(yàn)數(shù)據(jù)誤差不大于0.8%,判斷的失穩(wěn)點(diǎn)流量比實(shí)驗(yàn)值大1.2%;流場(chǎng)參數(shù)分布與實(shí)驗(yàn)結(jié)果吻合較好,能夠模擬出端壁黏性流動(dòng)與葉尖區(qū)流動(dòng)。三維黏性徹體力模型可以反映出壓氣機(jī)內(nèi)部流動(dòng)隨節(jié)流的變化情況,對(duì)于本文研究的三級(jí)壓氣機(jī),可以看到隨著節(jié)流流場(chǎng)細(xì)節(jié)的變化。

對(duì)多級(jí)壓氣機(jī)葉尖射流的擴(kuò)穩(wěn)效果實(shí)現(xiàn)了合理預(yù)測(cè),在100%設(shè)計(jì)轉(zhuǎn)速下,4.6%的設(shè)計(jì)點(diǎn)流量的射流流量帶來(lái)了7.06%的穩(wěn)定裕度增加,射流明顯增加了葉尖低能高熵值流體的軸向速度,消除了該位置的堵塞影響,使葉尖處工作在遠(yuǎn)離失穩(wěn)點(diǎn)狀態(tài),從而提高了壓氣機(jī)穩(wěn)定裕度。