隨機森林模型參數尋優算法比較分析

摘要：隨機森林模型有多種參數尋優算法，Python第三方庫scikit-learn給出了其中2種算法的具體實現，即網格搜索和隨機搜索。使用股票歷史交易數據集，根據當天的交易數據和技術指標預測未來一天的股票漲跌情況。首先，補充技術指標和分類標簽，對數據進行預處理；其次，將收盤價及10個技術指標視為特征變量，進行相關性分析，并在篩選之后對剩余的特征變量計算方差膨脹系數，最終保留5個特征變量；最后，對模型進行測試，使用網格搜索和隨機搜索對參數進行優化，比較二者的運行時長和在測試集上的準確率。結果發現，隨機搜索得到的一組最優參數在測試集上的準確率可達到61.9%，好于網格搜索的結果。實驗結果表明，在數據量大、參數范圍廣的情況下，隨機搜索算法比網格搜索算法具有更好的性能。

關鍵詞：隨機森林； Python； 網格搜索； 隨機搜索； 股票

中圖分類號：O224文獻標志碼：A

doi：10.3969/j.issn.1673-5862.2024.05.006

Comparative analysis of parameter optimization algorithms in random forest models

WANG Lizhu1， WU Pinkang1， WANG Qiuping2

（1.College of Mathematics and Systems Science， Shenyang Normal University， Shenyang 110034， China; 2.College of International Education， Shenyang Normal University， Shenyang 110034， China）

Abstract：

The random forest model has a variety of parameter optimization algorithms， and the Python third-party library scikit-learn gives the specific implementation of two algorithms， grid search and random search. Use a historical stock trading data set to predict the rise and fall of the next day based on the trading data and technical indicators of the day. Firstly， technical indicators and classification labels are supplemented to preprocess the data. The closing price and 10 technical indicators are regarded as characteristic variables， and the correlation analysis is carried out. After filtering， the variance expansion coefficient is calculated for the remaining feature variables， and finally five feature variables are retained. The model was subsequently tested. Grid search and random search were used to optimize the parameters， and the running time and accuracy on the test set of the two were compared. The accuracy of a set of optimal parameters obtained by random search on the test set can reach 61.9%， which is better than the results of grid search. The experimental results show that the random search algorithm has better performance than the grid search algorithm in the case of large amount of data and a wide range of parameters.

Key words：random forest； Python； grid search； random search； stock

算法模型可用于實際問題的研究和分析，例如投資策略［1-2］、疫情預測［3］、氣溫預測［4-5］、個人信用評估［6］等。隨機森林模型是一種算法模型，其應用廣泛，可解決分類問題，如文本分類、垃圾郵件識別、期刊評價［7］等問題，也可解決回歸問題，如房價預測、銷售量預測等問題。

股票的漲跌情況預測是一種分類問題，因而可以采用隨機森林模型來解決。國內有多名學者在這方面進行了研究。2017年，林娜娜等［8］首先運用相關性分析對初始指標體系進行篩選，然后采用手動搜索的方式對隨機森林的參數進行優化。2018年，方昕等［9］用離散二進制粒子群算法對技術指標進行選擇，篩選出最優特征，并采用手動搜索的方式對隨機森林的參數進行了優化。2020年，鄧晶和李路［10］選取5個純技術指標作為股票預測特征，采用網格搜索方法對隨機森林進行了參數尋優。2021年，王惠瑩和郝泳濤［11］以股票的5個技術指標和下周股價走勢作為隨機森林預測模型的特征，通過網格搜索優化隨機森林模型的參數。

國外在這方面也有一些相關研究。2021年，Sadorsky［12］使用隨機森林方法預測清潔能源股票價格，采用10倍交叉驗證和10次重復進行訓練控制來優化隨機森林模型參數，發現隨機森林和決策樹裝袋模型比邏輯回歸模型具有更高的預測準確性。2022年，Ghosh等［13］比較了隨機森林和LSTM網絡在預測Samp;P 500成分股日內交易價格方向變動的效果，引入多特征設置提高了預測準確性，并展示了不同模型和特征設置在不同時間段的表現及相關交易策略，其中隨機森林模型參數尋優使用的是基于經驗和實驗分析的方法。2024年，Meher等［14］使用隨機森林模型和高頻數據預測印度3家金融科技公司的股價，使用歷史交易數據進行實驗，通過交叉驗證調整超參數以優化模型性能，發現該模型預測效果良好。

為了使模型能夠取得良好的效果，往往需要對模型的參數進行優化。模型參數尋優的算法有很多，常見的是上面提到的手動搜索、網格搜索，除此之外，還有隨機搜索等算法。2017年，溫博文等［15］提出了一種基于改進的網格搜索的隨機森林參數優化算法。2022年，蔡明等［16］提出了一種基于自適應遺傳算法的隨機森林模型參數優化方法。

上述關于股票漲跌趨勢的研究在對隨機森林模型進行參數優化時，使用了手動搜索或網格搜索，均未使用隨機搜索算法。網格搜索算法的缺點是速度慢、耗時長、效率低，當數據量或者參數范圍大到一定程度時，其缺點尤為明顯。

為了探究隨機搜索算法對于隨機森林模型參數優化問題能否取得較好的效果，分析網格搜索和隨機搜索2種算法的性能差異，比較二者在運行時長和測試集上的準確率，本文使用股票歷史交易數據及Python和第三方庫scikit-learn進行實驗。首先，補充技術指標和分類標簽，對數據進行預處理；其次，將收盤價及10個技術指標視為特征變量，進行相關性分析，并在篩選之后對剩余的特征變量計算方差膨脹系數，最終保留5個特征變量；再次，劃分訓練集、測試集，對模型進行測試；最后，對網格搜索、隨機搜索這2種隨機森林模型參數尋優算法在運行時長和測試集上的準確率2個方面進行了比較。實驗結果表明隨機搜索算法取得了較好的效果。

1基礎知識

1.1決策樹模型

決策樹模型是隨機森林模型的基礎，這也是該模型名稱的由來。決策樹模型通過連續的邏輯判斷得出最后結論，其難點在于如何建立這樣一棵“樹”。具體而言，有2個主要的難點：1）根節點應該選擇哪一個特征；2）根節點特征選定之后的分類條件應該怎樣確定。這2個問題的解決辦法是統一的，解決問題依據的是計算得出的某種指標，例如信息熵、基尼系數。本文采用基尼系數這一指標。

1.2基尼系數

基尼系數可用于計算某種分類結果的混亂程度［17］。基尼系數越高，分類結果的混亂程度就越高，建立決策樹模型的目的就是降低分類結果的混亂程度，從而得到合適的數據分類效果。基尼系數的計算公式如下：

gini（T）=1-∑p2i

其中：pi為類別i在樣本T中出現的概率，即類別為i的樣本占總樣本個數的比率；∑為求和符號，表示對所有的p2i進行求和。

當引入某個用于分類的特征及條件時，分類后的基尼系數計算公式如下：

gini（T）=S1S1+S2gini（T1）+S2S1+S2gini（T2）

其中：S1和S2為劃分后的兩類各自的樣本量；gini（T1）和gini（T2）為兩類各自的基尼系數。

基尼系數越低表示分類結果的混亂程度越低，區分度越高，越適用于分類預測。實際應用中的數據量通常很大，不同情況下的基尼系數值的計算是人力難以完成的，需要利用機器不停地計算來找到基尼系數最低的特征及其分類條件，即最佳節點。選擇最佳節點作為根節點，根節點下面的子節點也同樣的方法來選擇。決策樹模型的2個核心難點問題由此得到解決。

1.3隨機森林模型

隨機森林模型是一個非常典型的集成學習模型。所謂集成學習模型，就是將多個模型組合在一起，產生一個更強大的模型。Bagging算法和Boosting算法是集成學習模型的2種常見算法。Bagging算法的原理類似投票，每個弱學習器都有一票，最終根據所有弱學習器的投票，按照少數服從多數的原則產生最終的分類結果。隨機森林模型是一種典型的Bagging模型，其弱學習器為決策樹模型。

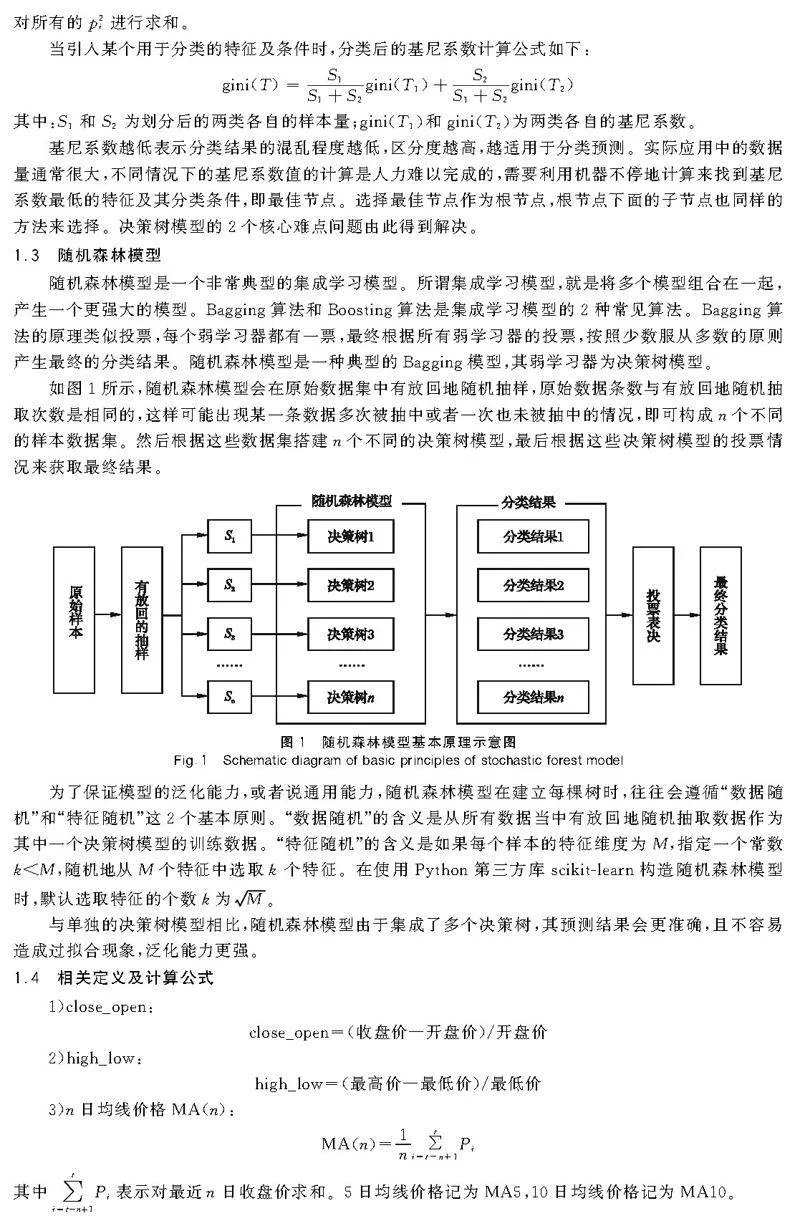
如圖１所示，隨機森林模型會在原始數據集中有放回地隨機抽樣，原始數據條數與有放回地隨機抽取次數是相同的，這樣可能出現某一條數據多次被抽中或者一次也未被抽中的情況，即可構成n個不同的樣本數據集。然后根據這些數據集搭建n個不同的決策樹模型，最后根據這些決策樹模型的投票情況來獲取最終結果。

為了保證模型的泛化能力，或者說通用能力，隨機森林模型在建立每棵樹時，往往會遵循“數據隨機”和“特征隨機”這2個基本原則。“數據隨機”的含義是從所有數據當中有放回地隨機抽取數據作為其中一個決策樹模型的訓練數據。“特征隨機”的含義是如果每個樣本的特征維度為M，指定一個常數klt;M，隨機地從M個特征中選取k個特征。在使用Python第三方庫scikit-learn構造隨機森林模型時，默認選取特征的個數k為M。

與單獨的決策樹模型相比，隨機森林模型由于集成了多個決策樹，其預測結果會更準確，且不容易造成過擬合現象，泛化能力更強。

1.4相關定義及計算公式

1）close_open：

close_open=（收盤價—開盤價）/開盤價

2）high_low：

high_low=（最高價—最低價）/最低價

3）n日均線價格MA（n）：

MA（n）=1n∑ti=t-n+1Pi

其中∑ti=t-n+1Pi表示對最近n日收盤價求和。5日均線價格記為MA5，10日均線價格記為MA10。

4）相對強弱指標RSI的計算公式：

RSI=N日平均上漲價格N日平均上漲價格+N日平均下跌價格×100

一般N的取值為6，12或24。

5）動量指標MOM的計算公式：

MOM=C-Cn

其中：C表示當前的收盤價；Cn表示n天前的收盤價。

6）指數移動平均值EMA的計算公式：

EMAtoday=αpricetoday+（1－α）EMAyesterday

其中：EMAtoday為當天的EMA值；pricetoday為當天的收盤價；EMAyesterday為昨天的EMA值；α為平滑指數，一般取值為2N+1，N表示天數。第一個EMA值通常為初始N天收盤價的均值。當N為12時，對應的EMA稱為EMA12。

7） 異同移動平均線MACD的計算公式：

MACD=2×（DIF-DEA）

DIF=EMA12-EMA26

DEA值是DIF值的9日加權移動均線值，計算方法類似EMA9，區別在于計算EMA9用的是收盤價，而計算DEA值用的是DIF值。

2網格搜索與隨機搜索算法的比較

隨機森林模型有多種參數尋優算法，Python第三方庫scikit-learn給出了2種算法的具體實現，即網格搜索和隨機搜索。scikit-learn官方文檔提供了二者的參數（表1和表2）。

網格搜索是指從指定的參數范圍中詳盡地生成參數組合候選項，不遺漏任何一種可能的參數組合，然后在所有候選的參數組合中，通過循環遍歷，嘗試每一種可能性，表現最好的一組參數就是最終的結果，即最優參數。

隨機搜索是指從指定的參數范圍中隨機抽取參數，生成指定數量的參數組合候選項。在這些候選的參數組合中，通過循環遍歷，嘗試每一種可能性，表現最好的一組參數就是最終的結果，即最優參數。

通過對比可以發現，隨機搜索比網格搜索多2個參數，即n_iter和random_state。參數n_iter設置生成指定數量的參數組合候選項，參數random_state為隨機狀態，設置具體值后，每次隨機搜索的結果保持不變。

2012年，加拿大蒙特利爾大學的2位學者Bergstra和Bengio［18］研究發現，與純網格搜索配置的神經網絡相比，在同一域上的隨機搜索能夠在很少的計算時間內找到同樣好或更好的模型。

3實驗及結果分析

本實驗使用的數據集是芯源微（688037）從2019年12月16日至2023年4月10日共804個交易日的數據，通過軟件“同花順遠航版8.6.1.2”得到。實驗使用的程序設計語言是Python 3.11，調用的第三方庫內scikit-learn 1.2.1。實驗根據當天的交易數據和技術指標對未來一天的漲跌情況進行分類，通過運行時長和測試集上的分類準確率反映2種參數尋優算法的性能差異。

補充技術指標和分類標簽之后產生大量空值，將含有空值的數據剔除，剩余770條數據。按照日期順序，把2020年2月10日至2022年12月30日數據作為訓練集，2023年1月3日至2023年4月7日數據作為測試集。訓練集用來訓練模型和參數優化，測試集用來對模型進行測試。

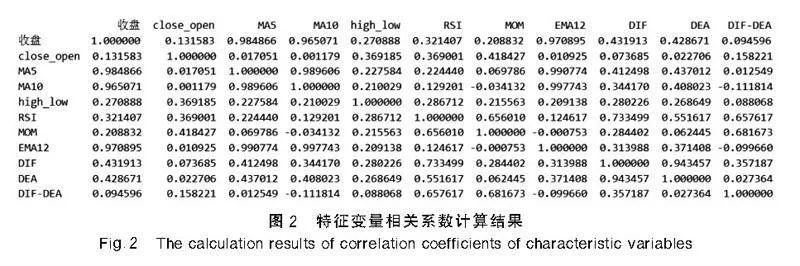
將收盤價和10個技術指標視為特征變量，計算它們的Pearson相關系數（圖2），進行相關性分析。若2個特征變量相關系數很大，表明二者相關性非常強，將導致多重共線性，因而需要刪去其中之一。經過篩選，剔除收盤價、MA10、EMA12、DEA。

然后對剩余的特征變量計算方差膨脹系數，系數值越大表示多重共線性越嚴重，當系數值小于10時，認為不存在多重共線性。當系數值在10至100之間時，認為存在較強的多重共線性。因此，剔除MA5和RSI。最終剩下close_open，high_low，MOM，DIF，DIF-DEA這5個特征變量。

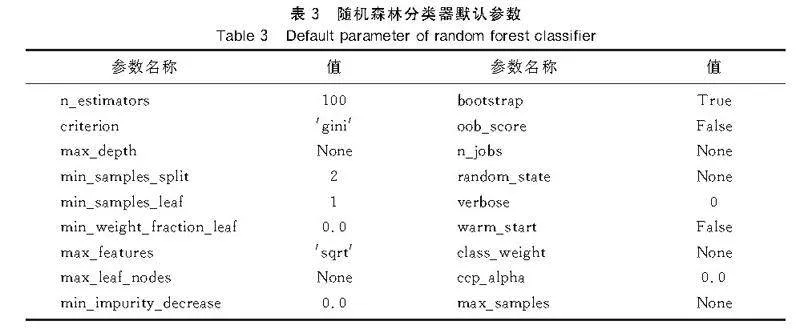
Python第三方庫scikit-learn給出了隨機森林分類器random forest classifier的具體實現，提供了默認參數（表3），即n_estimators=100，min_samples_leaf=1，max_depth=None。max_depth=None含義是擴展節點直到所有葉子都是純的，或者直到所有葉子包含的樣本少于min_samples_split，而min_samples_split默認為2。在這組默認參數的情況下，測試集上準確率得分為0.587301。

使用網格搜索，設置交叉驗證參數cv=3，參數n_estimators記為n_e，參數max_depth記為m_d，參數min_samples_leaf記為m_s_l，結果見表4。

由此可見，網格搜索耗時較長，只將其中一個參數范圍擴大為原來的2倍，耗時就變為原來的4倍，隨著數據量和參數范圍的擴大，耗時將會持續增加，而尋找到的最優參數在測試集上的準確率未必會有明顯提升，甚至不如默認參數在測試集上的準確率。

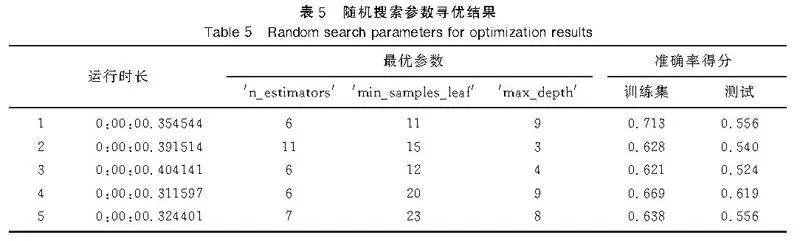
使用隨機搜索，設置交叉驗證參數cv=3，對于參數范圍5lt; n_estimatorslt;20，1lt; max_depthlt;10，1lt; min_samples_leaflt;30，結果見表5。

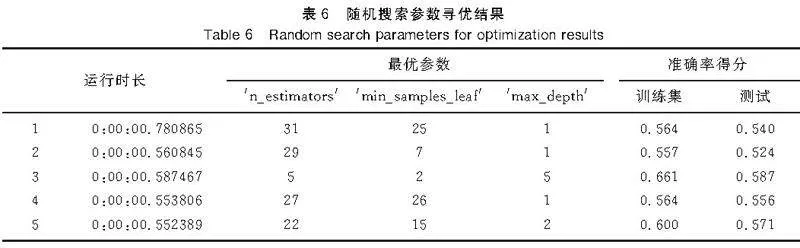
使用隨機搜索，設置交叉驗證參數cv=3，對于參數范圍5lt; n_estimatorslt;40，1lt; max_depthlt;10，1lt; min_samples_leaflt;30，結果見表6。

由此可見，隨機搜索速度快，耗時短。將其中一個參數范圍擴大為原來的2倍，耗時雖有增加，但仍不超過1s。隨著數據量和參數范圍的擴大，網格搜索耗時將超過1h，而隨機搜索仍然可在2s左右的時間內完成。相比于網格搜索的耗時，隨機搜索耗時可以忽略不計。

在測試集的準確率上，隨機搜索也表現出較好的效果。對于不同的參數范圍，分別進行5次隨機搜索得到5組最優參數，能夠得到一組參數在測試集上的準確率得分較為理想，準確率最高可達62%。

4結語

不同的參數尋優算法有不同的優點和缺點。網格搜索算法的缺點是速度慢、耗時長、效率低，當數據量或者參數范圍大到一定程度時，其缺點尤為明顯。隨機搜索算法與其相反，具有速度快、耗時短、效率高的優點，當數據量或者參數范圍大到一定程度時，其優點尤為明顯，可以比網格搜索算法更好地完成參數尋優任務，甚至只能用隨機搜索算法來完成。

網格搜索和隨機搜索的區別在于，網格搜索遍歷每一種參數組合，耗時較長，隨機搜索不會對每一種參數組合進行遍歷，而是隨機抽取指定數量的若干組參數組合，然后對這若干組參數組合進行遍歷，多次隨機搜索便有可能搜索到效果較為理想的一組參數。對于參數范圍比較廣或者數據量比較大的情況，隨機搜索的性價比要優于網格搜索。

無論是網格搜索還是隨機搜索，都是將訓練集劃分成幾等份，利用交叉驗證思想得到一組最優參數，但并不意味著在未經訓練的測試集上仍然是最優參數，所謂的最優參數在測試集上的分類準確度也可能很不理想。

參考文獻：

［1］KRAJCINOVIC D，FONSEKA G U.The continuous damage theory of brittle materials［J］.J Appl Mech，1981，48（4）：809-824.王立柱，宋欽欽.基于均線及統計規律的股票投資策略［J］.沈陽師范大學學報（自然科學版），2021，39（6）：527-530.

［2］曹正鳳，紀宏，謝邦昌.使用隨機森林算法實現優質股票的選擇［J］.首都經濟貿易大學學報，2014，16（2）：21-27.

［3］王劍輝，蔣杏麗.基于LSTM模型對印度新冠肺炎疫情的預測［J］.沈陽師范大學學報（自然科學版），2022，40（6）：554-557.

［4］趙成兵，劉丹秀，謝新平，等.基于時間序列的季節性氣溫預測研究［J］.安徽建筑大學學報，2022，30（3）：83-89.

［5］陶曄，杜景林.基于隨機森林的長短期記憶網絡氣溫預測［J］.計算機工程與設計，2019，40（3）：737-743.

［6］王重仁，韓冬梅.基于超參數優化和集成學習的互聯網信貸個人信用評估［J］.統計與決策，2019，35（1）：87-91.

［7］溫學兵，謝維，姚佳宜.基于隨機森林和支持向量機模型的期刊評價［J］.沈陽師范大學學報（自然科學版），2022，40（2）：174-179.

［8］林娜娜，秦江濤.基于隨機森林的A股股票漲跌預測研究［J］.上海理工大學學報，2018，40（3）：267-273，301.

［9］方昕，李旭東，曹海燕，等.基于改進隨機森林算法的股票趨勢預測［J］.杭州電子科技大學學報（自然科學版），2019，39（2）：22-27.

［10］鄧晶，李路.參數優化隨機森林在股票預測中的應用［J］.軟件，2020，41（1）：178-182.

［11］王惠瑩，郝泳濤.基于技術指標和隨機森林的股價走勢預測算法［J］.現代計算機，2021，27（27）：43-47，52.

［12］SADORSKY P.A random forests approach to predicting clean energy stock prices［J］.J Risk and Financial Manag，2021，14（2）：48.

［13］GHOSH P，NEUFELD A，SAHOO J K.Forecasting directional movements of stock prices for intraday trading using LSTM and random forests［J］.Financ Res Lett，2022，46：102280.

［14］MEHER B K，SINGH M，BIRAU R，et al.Forecasting stock prices of fintech companies of India using random forest with high-frequency data［J］.J Open Innovation：Technology，Market，and Complexity，2024，10（1）：100180.

［15］溫博文，董文瀚，解武杰，等.基于改進網格搜索算法的隨機森林參數優化［J］.計算機工程與應用，2018，54（10）：154-157.

［16］蔡明，孫杰，楊維發，等.基于自適應遺傳算法的隨機森林模型參數優化方法［J］.智能計算機與應用，2022，12（12）：175-179.

［17］王宇韜，錢妍竹.Python大數據分析與機器學習商業案例實戰［M］.北京：機械工業出版社，2020.

［18］BERGSTRA J，BENGIO Y.Random search for hyper-parameter optimization［J］.J Mach Learn Res，2012，13（2）：281-305.

【責任編輯：溫學兵】

收稿日期：2023-06-08

基金項目：遼寧省教育科學規劃一般項目（JG20DB419）； 遼寧省檔案科技項目（2023-B-025）。

作者簡介：

王立柱（1979—），男，遼寧營口人，沈陽師范大學副教授，博士; 通信作者：王秋萍（1982—），女，遼寧沈陽人，沈陽師范大學副教授，博士。