帶拒絕、惡化和安裝時(shí)間的工期指派單機(jī)排序

摘要：研究了帶有p-s-d安裝時(shí)間的單機(jī)排序問題。工件的實(shí)際加工時(shí)間與加工的位置有關(guān)，工件的加工位置越延后，工件的加工時(shí)間越長。將工件集分為拒絕工件集和接收工件集，被拒絕的工件需要支付拒絕懲罰。討論了在公共工期（common due-date，CON）、松弛工期（slack due-date，SLK）和不同工期（different due-date，DIF）指派下，目標(biāo)函數(shù)為提前、誤工、提前的工件數(shù)量、誤工的工件數(shù)量、工期大小、最大完工時(shí)間、拒絕懲罰及總完工時(shí)間絕對差的加權(quán)和問題。目的是確定工件的最優(yōu)排序，使目標(biāo)函數(shù)極小化。將上述問題轉(zhuǎn)化為指派問題，從中選取目標(biāo)函數(shù)值最小的解為最優(yōu)解。對于上述問題，推廣了已有文獻(xiàn)的模型，給出了多項(xiàng)式時(shí)間算法，算法的時(shí)間復(fù)雜度為O（n4），并用數(shù)值例子進(jìn)行了驗(yàn)證。

關(guān)鍵詞：拒絕; 工期; 惡化效應(yīng); 安裝時(shí)間

中圖分類號：O224文獻(xiàn)標(biāo)志碼：A

doi：10.3969/j.issn.1673-5862.2024.05.011

Single-machine due-date assignment scheduling with rejection

deterioration effects and setup times

ZHAO Yufang， LI Meiqi， FENG Wanting

（College of Mathematics and Systems Science， Shenyang Normal University， Shenyang 110034， China）

Abstract：

Consider the single-machine scheduling problem with p-s-d setup times. The actual processing time of the job is related to the processing position. The processing position of the job is later， the processing time of the job will be longer. We divide the job sets into rejected job sets and received job sets， and the rejected job needs to pay a rejection penalty. Under common due-date （CON）， slack due-date （SLK） and different due-date （DIF）， the objective function is the weighted sum problem of earliness-tardiness， number of early/delayed jobs，due-date cost， makespan， the rejection penalty and the total absolute differences in completion times. The purpose is to determine the optimal scheduling of jobs such that minimizes the objective function. Transform the above problem into an assignment problem and find the optimal solution in it. Provided an algorithm that can be solved in polynomial time. The time complexity of the algorithm is O（n4）， and numerical examples are used to verify it. The existing models are generalized.

Key words：

rejection; due-date; deterioration effect; setup times

在實(shí)際生產(chǎn)中，如果客戶的訂單生產(chǎn)成本太高或加工時(shí)間太長，制造商會(huì)選擇拒絕加工這些工件并支付相應(yīng)的拒絕懲罰。在制造商加工工件的過程中，惡化效應(yīng)是經(jīng)常存在的，例如機(jī)器在加工工件時(shí)，會(huì)出現(xiàn)損耗等情況，所以工件在機(jī)器中加工位置越延后，其加工時(shí)間越長。

帶有惡化效應(yīng)的問題最早是由Browne和Yechiali［1］提出的。Sun和Geng［2］研究了帶有惡化效應(yīng)和機(jī)器維修活動(dòng)的單機(jī)排序問題（所有工件的惡化率相同，工件的實(shí)際加工時(shí)間是開始時(shí)間的線性增函數(shù)，目的是分別極小化最大完工時(shí)間和總完工時(shí)間），證明了這2個(gè)問題都是多項(xiàng)式時(shí)間內(nèi)可解的。Huang等［3］研究了線性惡化效應(yīng)和公共工期窗口的單機(jī)排序問題，證明了2個(gè)問題在多項(xiàng)式時(shí)間內(nèi)可解（第1個(gè)問題的目標(biāo)函數(shù)為提前工件的數(shù)量、誤工工件的數(shù)量、窗口大小和工期加權(quán)和，第2個(gè)問題的目標(biāo)函數(shù)為提前、誤工、窗口大小和工期加權(quán)和）。Lin［4］研究了帶有惡化效應(yīng)、學(xué)習(xí)效應(yīng)和工期窗口的單機(jī)排序問題（其中權(quán)重取決于工件在加工過程中的位置，目的是極小化提前、誤工、窗口開始時(shí)間和窗口大小的加權(quán)和），對3種工期窗口（CONW、SLKW、DIFW）指派問題給出了復(fù)雜度為O（n3）的多項(xiàng)式時(shí)間算法。對于同時(shí)考慮拒絕和惡化效應(yīng)的問題，Nian和Mao［5］研究了帶有3種實(shí)際加工時(shí)間的單機(jī)排序問題，證明了總完工時(shí)間與總拒絕懲罰的加權(quán)和可以在多項(xiàng)式時(shí)間內(nèi)解決。

對于帶有p-s-d安裝時(shí)間的問題，Wang［6］研究了單機(jī)工期指派問題（目的是極小化提前、誤工、提前和誤工的工件數(shù)量及工期大小的線性加權(quán)和，在公共工期、松弛工期、不同工期指派下），證明了它們都可以在多項(xiàng)式時(shí)間內(nèi)求解。Soroush［7］解決了具有p-s-d安裝時(shí)間和基于工件依賴位置的學(xué)習(xí)效應(yīng)的雙準(zhǔn)則單機(jī)排序問題（其中工件的安裝時(shí)間是已加工工件的實(shí)際加工時(shí)間的函數(shù)，目標(biāo)函數(shù)分別是最大完工時(shí)間、總延誤工、總完工時(shí)間絕對差及提前、誤工、公共工期懲罰的線性函數(shù)），證明了這些問題不能在多項(xiàng)式時(shí)間內(nèi)求解，但可以用分支定解法來獲得最優(yōu)排序。在帶有p-s-d安裝時(shí)間和學(xué)習(xí)效應(yīng)的基礎(chǔ)上，F(xiàn)eng等［8］又考慮了帶有工期的情況，其中工件加工時(shí)間是非遞增函數(shù)。在3種工期（CON，SLK，DIF）指派下，目的是極小化提前、誤工、提前的工件數(shù)量、誤工的工件數(shù)量和工期分配成本的加權(quán)總和，其中權(quán)重與位置相關(guān)，分別提出了多項(xiàng)式時(shí)間內(nèi)可解的算法。Huang等［9］研究了帶有p-s-d安裝時(shí)間、惡化效應(yīng)依賴時(shí)間和學(xué)習(xí)效應(yīng)依賴位置的單機(jī)排序問題（其中工件的實(shí)際加工時(shí)間不僅是已加工工件的總普通加工時(shí)間的非減函數(shù)，也是工件在排序中位置的非減函數(shù)，目的是極小化最大完工時(shí)間及總完工時(shí)間等），分別給出了多項(xiàng)式時(shí)間內(nèi)可解的算法。對于同時(shí)考慮拒絕和p-s-d安裝時(shí)間，Liu等［10］研究了工期窗口單機(jī)排序問題（目標(biāo)函數(shù)為提前、誤工、提前的工件數(shù)量、誤工的工件數(shù)量、工期及拒絕懲罰加權(quán)和），證明了該問題是多項(xiàng)式時(shí)間內(nèi)可解的。Wang等［11］又研究了帶有惡化效應(yīng)的單機(jī)排序問題（其中工件的實(shí)際加工時(shí)間取決于該工件在排序中的位置，目的是極小化最大完工時(shí)間與拒絕懲罰之和、總完工時(shí)間與拒絕懲罰之和、完工時(shí)間的總絕對差與拒絕懲罰之和、加工工件的等待時(shí)間總絕對差與拒絕懲罰之和），證明了這些問題是多項(xiàng)式時(shí)間內(nèi)可解的。對于帶有拒絕工件的問題，Gerstl和Mosheiov［12］研究了帶有工期和拒絕工件的單機(jī)排序問題（其中工期依賴于工件在加工過程中的位置，目標(biāo)函數(shù)分別是最大誤工和拒絕懲罰之和、總誤工和拒絕懲罰之和），證明了問題都是NP難的，給出了偽多項(xiàng)式動(dòng)態(tài)規(guī)劃算法和啟發(fā)式算法。Shabtay等［13］對此進(jìn)行了綜述。

本文在Wang［6］和Liu等［10］研究的基礎(chǔ)上進(jìn)行了推廣，研究了帶有拒絕、CON/SLK/DIF、惡化效應(yīng)和安裝時(shí)間的單機(jī)排序問題（目的是極小化提前、誤工、提前的工件數(shù)量、誤工的工件數(shù)量、工期大小、最大完工時(shí)間、拒絕懲罰及總完工時(shí)間絕對差的加權(quán)和），給出了多項(xiàng)式時(shí)間算法。

1問題描述

有一臺機(jī)器和n個(gè)工件{J1，J2，…，Jn}，所有工件從0時(shí)刻開始加工且不允許中斷，工件要么被接受，要么被拒絕。工件Jj的基本加工時(shí)間為pj，實(shí)際加工時(shí)間為

pAj=pjrβj，j，r=1，2，…，na

其中：βj表示工件Jj的惡化率；Cj表示加工時(shí)間；ej表示拒絕懲罰；r表示工件Jj排在第r個(gè)位置加工；A表示接受工件的集合；R表示拒絕工件的集合；na表示接受工件的數(shù)量，［r］表示排在第r個(gè)位置的工件。工件J［j］的安裝時(shí)間為

s［j］=b∑j－1h=1pA［h］，j=1，2，…，na，bgt;0

其中：Ej=max{0，dj－Cj}表示工件Jj的提前；Tj=max{0，Cj－dj}表示工件Jj的誤工。如果Cjlt;dj，則Uj=1，否則Uj=0；如果Cjgt;dj，則Vj=1，否則Vj=0。對于CON問題，dj=dopt（j=1，2，…，n）。對于SLK指派問題，dj=sj+pAj+qopt。對于DIF指派模型，也就是每個(gè)工件可以不受限制的被分配不同的工期，此時(shí)工件Jj的工期為dj。Cmax表示最大完工時(shí)間，TADC表示總完工時(shí)間絕對差。目的是極小化以下目標(biāo)函數(shù)：

F=∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θdopt/qopt/dj）+αCmax+δTADC+∑j∈Rej（1）

其中：κ，λ，θ，α，δ為大于等于0且已給定的常數(shù)；uj，vj分別為工件Jj提前和誤工的單位懲罰。

問題的三參數(shù)描述為

1|pAj=pjrβj|∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θdopt/qopt/dj）+αCmax+δTADC+∑j∈Rej

2CON指派問題

設(shè)CON指派問題的目標(biāo)函數(shù)為

F1=∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θdopt）+αCmax+δTADC+∑j∈Rej

首先給出2個(gè)基本引理。

引理1對于給定的排序π，dopt的值一定為某一工件的完工時(shí)間，即dopt=C［μ］。

證明反證法。若工期dopt取在工件J［μ］加工過程中，即C［μ－1］lt;doptlt;C［μ］，則此時(shí)目標(biāo)函數(shù)為

F1=∑μ－1j=1κ（dopt－C［j］）+∑naj=μλ（C［j］－dopt）+∑μ－1j=1u［j］+∑naj=μv［j］+naθdopt+αCmax+δTADC+∑j∈Rej當(dāng)dopt=C［μ－1］時(shí)，

F′1=∑μ-1j=1κ（C［μ-1］-C［j］）+∑naj=μλ（C［j］-C［μ-1］）+∑μ-2j=1u［j］+∑naj=μv［j］+naθC［μ-1］+αCmax+δTADC+∑j∈Rej當(dāng)dopt=C［μ］時(shí)，

F″1=∑μ-1j=1κ（C［μ］-C［j］）+∑naj=μ+1λ（C［j］-C［μ］）+∑μ-1j=1u［j］+∑naj=μ+1v［j］+naθC［μ］+αCmax+δTADC+

∑j∈RejF1-F′1=（μ-1）κ（dopt-C［μ-1］）-λ（na-μ+1）（dopt-C［μ-1］）+u［μ-1］+naθ（dopt-C［μ-1］）=

［（μ－1）κ－λ（na－μ+1）+naθ］（dopt－C［μ－1］）+u［μ－1］

F1-F″1=（μ-1）κ（dopt-C［μ］）-λ（na-μ+1）（dopt-C［μ］）+v［μ］+naθ（dopt-C［μ］）=

［（μ－1）κ－λ（na－μ+1）+naθ］（dopt－C［μ］）+v［μ］

若（μ－1）κ－λ（na－μ+1）≥naθ，則F1≥

F′1；若（μ－1）κ－λ（na－μ+1）≤naθ，則F1≥F″1。也就是說，dopt取在某一工件的完工時(shí)間一定優(yōu)于某一工件的加工過程中，即最優(yōu)排序中的最優(yōu)工期一定為某個(gè)工件的完工時(shí)間，不會(huì)在某一工件的加工過程中。

與Liu等［10］類似，有如下結(jié)論：

引理2若u［j］=v［j］=0，則對于給定一個(gè)排序π，當(dāng)dopt=C［μ］時(shí)，目標(biāo)函數(shù)值最優(yōu)，其中

μ=na（λ－θ）κ+λ（2）

2.1公式推導(dǎo)

對于給定的排序π=（A，R），其中A為接受工件的集合，記na=|A|。與Wang等［11］類似，給定排序π，其中第1個(gè)工件在0時(shí)刻被加工并且機(jī)器在加工過程中沒有空閑。設(shè)C［j］表示排在第j個(gè)位置的完工時(shí)間，則

C［1］=s［1］+pA［1］=pA［1］

C［2］=C［1］+s［2］+pA［2］=pA［1］+bpA［1］+pA［2］=

（1+b）pA［1］+pA［2］

C［3］=C［2］+s［3］+pA［3］=（1+2b）pA［1］+（1+b）pA［2］+pA［3］

C［4］=C［3］+s［4］+pA［4］=（1+2b）pA［1］+（1+b）pA［2］+pA［3］+bpA［1］+bpA［2］+bpA［3］+pA［4］=

（1+3b）pA［1］+（1+2b）pA［2］+（1+b）pA［3］+pA［4］

…

C［j］=∑jr=1（s［r］+pA［r］）=∑jr=1［1+b（j－r）］pA［r］，j=1，2，…，na （3）

于是

Cmax=∑naj=1［1+b（na－j）］pA［j］，j=1，2，…，na（4）

∑j∈RCj=∑naj=1（na－j+1）1+na－j2bpA［j］（5）

下面利用式（2）和式（3）推導(dǎo)工期為CON的目標(biāo)函數(shù)表達(dá)式F1。

1）F1中的第1部分為

∑j∈AκE［j］=∑μ－1j=1κE［j］=∑μ－1j=1κ（C［μ］－C［j］）=∑μ－1j=1κ（∑μξ=1［1+b（μ－ξ）］pA［ξ］－∑jξ=1［1+b（j－ξ）］pA［ξ］）（6）

2）F1中的第2部分為

∑j∈AλT［j］=∑naj=μ+1λT［j］=∑naj=μ+1λ（C［j］－C［μ］）=∑naj=μ+1λ（∑jξ=1［1+b（j－ξ）］pA［ξ］－∑jξ=1［1+b（μ－ξ）］pA［ξ］）（7）

3）F1中的第3部分為

∑j∈Au［j］U［j］=∑μ－1j=1u［j］U［j］=∑μ－1j=1u［j］（8）

4）F1中的第4部分為

∑j∈Av［j］V［j］=∑naj=μ+1v［j］V［j］=∑naj=μ+1v［j］（9）

5）F1中的第5部分為

∑j∈Aθdopt=naθdopt=naθC［μ］=naθ∑μj=1［1+b（μ－j）］pA［j］（10）

6）F1中的第6部分為

αCmax=α∑naj=1［1+b（na－j）］pA［j］ （11）

7）F1中的第7部分為

δTADC=δ∑naj=1∑nak=j+1|C［k］－C［j］|

=δ|C［2］－C［1］+C［3］－C［1］+…+C［na］－C［1］+C［3］－C［2］+C［4］－C［2］+…+C［na］－C［na－1］|

=δ∑naj=1（2j－na－1）C［j］

=δ∑naj=1（2j－na－1）∑jr=1［1+b（j－r）］pA［r］

=δ（1－na）pA［1］+δ（3－na）［（1+b）pA［1］+pA［2］］+…+δ（na－1）［（1+（na－1）b）pA［1］+…+（1+b）pA［na－1］+pA［na］］

=δ∑naj=1∑nah=j（2h－na－1）［1+（h－j）b］pA［j］j=1，2，…，na（12）

綜上，將式（6—12）代入目標(biāo)函數(shù)表達(dá)式F1中，可得

F1=∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θdopt）+αCmax+δTADC+∑j∈Rej

=∑μ－1j=1κ（C［μ］－C［j］）+∑naj=μ+1λ（C［j］－C［μ］）+∑μ－1j=1u［j］+∑naj=μ+1v［j］+naθ∑μj=1［1+b（μ－j）］pA［j］+

α∑naj=1［1+b（na－j）］pA［j］+δ∑naj=1∑nah=j（2h－na－1）［1+b（h－j）］pA［j］+∑j∈Rej

=∑μ－1j=1κ（∑μξ=1［1+b（μ－ξ）］pA［ξ］－∑jξ=1［1+b（j－ξ）］pA［ξ］）+

∑naj=μ+1λ（∑jξ=1［1+b（j－ξ）］pA［ξ］－∑μξ=1［1+b（μ－ξ）］pA［ξ］）+∑μ－1j=1u［j］+∑naj=μ+1v［j］+

naθ∑μj=1［1+b（μ－j）］pA［j］+α∑naj=1［1+b（na－j）］pA［j］+

δ∑naj=1∑nah=j（2h－na－1）［1+b（h－j）］pA［j］+∑j∈Rej

=∑naj=1ψjpA［j］+∑μ－1j=1u［j］+∑naj=μ+1v［j］+∑j∈Rej

其中

ψj=

κ（j－1）（1+b（μ－j））+λb（na－μ+1）（na－μ）2+naθ［1+b（μ－j）］+α（1+b（na－j））+δ∑nah=j（2h－na－1）［1+b（h－j）］j=1，2，…，μλ［2+b（na－j）］（na－j+1）2+α（1+b（na－j））+δ∑nah=j（2h－na－1）［1+b（h－j）］j=μ+1，…，na

2.2問題求解

若接受工件的個(gè)數(shù)為na，工期取在第μ個(gè)位置，即dopt=C［μ］。則在排序π中，設(shè)工件Jj在第r個(gè)位置加工，xjr=1；否則xjr=0。于是1|pAj=pjrβj|F1可以轉(zhuǎn)化成以下指派問題：

min∑nj=1∑nr=1ωnajrxjr

∑nj=1xjr=1r=1，2，…，n∑nr=1xjr=1j=1，2，…，nxjr∈{0，1}

其中

ωjr=ψrpjrβj+ujr=1，2，…，μ－1

ψrpjrβjr=μ

ψrpjrβj+vjr=μ+1，…，na

ejr=na+1，…，n （13）

令F1（na）表示有na個(gè)工件被接受時(shí)由指派問題得到的目標(biāo)函數(shù)值。當(dāng)na=0時(shí)，表示所有工件都被拒絕，這時(shí)目標(biāo)函數(shù)值為F1（0）=∑nj=1ej，可以用以下算法來求解。

算法1

第1步計(jì)算初始值F1（0）=∑nj=1ej；

第2步依次令na=1，2，…，n，根據(jù)式（1）和式（13）計(jì)算μ和ωjr，求解對應(yīng)指派問題，得到函數(shù)值F1（na）；

第3步計(jì)算最優(yōu)值F*1=min{Fna|na=0，1，2，…，n}。

接下來分析算法的復(fù)雜性。

定理1問題1|pAj=pjrβj|F1的復(fù)雜度為O（n4）。

證明 算法第1步的復(fù)雜度為O（n）；第2步求解每個(gè)指派問題的復(fù)雜度為O（n3），共需解n－1個(gè)指派問題，故復(fù)雜度為O（n4）；第3步的復(fù)雜度為O（n）。故算法復(fù)雜度為O（n4）。

例1設(shè)有6個(gè)工件，κ=8，λ=6，θ=5，α=2，δ=1，b=1，用算法1求解目標(biāo)函數(shù)最優(yōu)值。

解：

當(dāng)na=0時(shí)，F(xiàn)1（0）=∑6j=1ej=e1+e2+e3+e4+e5+e6=868；當(dāng)na=1時(shí)，由式（2）計(jì)算得到 μ=1，由式（13）得到如下矩陣：

ωjr=491301301301301306314114114114114142145145145145145771501501501501502114714714714714784155155155155155

通過指派問題求得最優(yōu)解，此時(shí)只接受工件5，目標(biāo)值為F1（1）=742。

同上，當(dāng)na=2時(shí)，μ=1，得到接受工件為工件1和工件5，加工順序?yàn)锳=［5，1］，目標(biāo)值為F1（2）=752；當(dāng)na=3時(shí)，μ=1，得到接受工件為1，3，5，加工順序?yàn)锳=［3，5，1］，目標(biāo)值為F1（3）=1085；當(dāng)na=4時(shí)，μ=1，接受工件為2，3，4，5，加工順序?yàn)锳=［2，5，4，3］，目標(biāo)值為F1（4）=2070；當(dāng)na=5時(shí)，μ=1，接受工件為1，2，3，4，5，加工順序?yàn)锳=［2，5，3，1，4］，目標(biāo)值為F1（5）=4787；當(dāng)na=6時(shí)，所有工件都被加工，計(jì)算得μ=1，加工順序?yàn)锳=［4，3，5，1，2，6］，目標(biāo)值為F1（6）=8672。

綜上，比較目標(biāo)函數(shù)值，只接受1個(gè)工件5最好，F(xiàn)*1=742。

3SLK指派問題

設(shè)SLK指派問題的目標(biāo)函數(shù)為

F2=∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θqopt）+αCmax+δTADC+∑j∈Rej

與引理1和引理2類似，有如下2個(gè)基本引理：

引理3對于給定排序π，qopt的值一定為某一工件的完工時(shí)間。

證明 反證法。若工期qopt取在工件J［μ］加工過程中，即C［μ－1］lt;qoptlt;C［μ］，則此時(shí)目標(biāo)函數(shù)為

F2=∑μ－1j=1κ（d［j］－C［j］）+∑naj=μ+1λ（C［j］－d［j］）+∑μ－1j=1u［j］+∑naj=μ+1v［j］+naθqopt+αCmax+δTADC+∑j∈Rej=∑μ－1j=1κ（s［j］+pA［j］+qopt－C［j］）+∑naj=μ+1λ（C［j］－s［j］－pA［j］－qopt）+∑μ－1j=1u［j］+∑naj=μ+1v［j］+naθqopt+αCmax+δTADC+∑j∈Rej

當(dāng)qopt=C［μ－1］時(shí)，

F′2=∑μ-1j=1κ（s［j］+pA［j］+C［μ-1］-C［j］）+∑naj=μ+1λ（C［j］-s［j］-pA［j］-C［μ-1］）+∑μ-2j=1u［j］+∑naj=μ+1v［j］+naθC［μ-1］+αCmax+δTADC+∑j∈Rej

當(dāng)qopt=C［μ］時(shí)，

F″2=∑μ-1j=1κ（s［j］+pA［j］+C［μ］-C［j］）+∑naj=μ+1λ（C［j］-s［j］-pA［j］-C［μ］）+∑μ-1j=1u［j］+∑naj=μ+1v［j］+naθC［μ］+αCmax+δTADC+∑j∈Rej

F2-F′2=［（μ-1）κ-λ（na-μ+1）+naθ］（qopt-C［μ-1］）+u［μ-1］

F2-F″2=［（μ-1）κ-λ（na-μ+1）+naθ］（qopt-C［μ］）+v［μ］

若（μ－1）κ－λ（na－μ+1）≥naθ，則F2≥F2′；若（μ－1）κ－λ（na－μ+1）≤naθ，則F2≥F″2。qopt取在某工件完工時(shí)刻一定優(yōu)于某工件加工過程中。因此，最優(yōu)排序中的最優(yōu)工期一定為某個(gè)工件的完工時(shí)間，不會(huì)在某一工件的加工過程中。即qopt的值一定為某一工件的完工時(shí)間。

引理4與Liu等［10］類似，有如下結(jié)論。若u［j］=v［j］=0，則對于給定的排序π，當(dāng)qopt=C［μ－1］時(shí)，目標(biāo)函數(shù)值最優(yōu)，其中

μ=na（λ－θ）κ+λ（14）

3.1公式推導(dǎo)

對于給定的排序π=（A，R），其中A為接受工件的集合，記na=|A|。根據(jù)引理4，令qopt=C［μ－1］。下面利用式（2）和式（3）推導(dǎo)工期為SLK的目標(biāo)函數(shù)表達(dá)式F2如下：

1）F2中的第1部分為

∑j∈AκE［j］=∑μ－1j=1κE［j］=∑μ－1j=1κ（d［j］－C［j］）=∑μ－1j=1κ（s［j］+pA［j］+C［μ－1］－C［j］）=∑μ－1j=1κ（C［μ－1］－C［j－1］）

=∑μ－1j=1κ（∑μ－1ξ=1［1+b（μ－1－ξ）］pA［ξ］－∑j－1ξ=1［1+b（j－1－ξ）］pA［ξ］）（15）

2）F2中的第2部分為

∑j∈AλT［j］=∑naj=μ+1λT［j］=∑naj=μ+1λ（C［j］－d［j］）=∑naj=μ+1λ（C［j］－s［j］－pA［j］－C［μ－1］）=∑naj=μ+1λ（C［j－1］－C［μ－1］）=∑naj=μλ（∑j－1ξ=1［1+b（j－1－ξ）］pA［ξ］－∑j－1ξ=1［1+b（μ－1－ξ）］pA［ξ］）（16）

3）F2中的第3部分為

∑j∈Au［j］U［j］=∑μ－1j=1u［j］U［j］=∑μ－1j=1u［j］（17）

4）F2中的第4部分為

∑j∈Av［j］V［j］=∑naj=μ+1v［j］V［j］=∑naj=μ+1v［j］（18）

5）F2中的第5部分為

∑j∈Aθqopt=naθqopt=naθC［μ－1］=naθ∑μ－1j=1［1+b（μ－1－j）］pA［j］ （19）

6）F2中的第6部分為

αCmax=α∑naj=1［1+b（na－j）］pA［j］（20）

7）F2中的第7部分為

δTADC=δ∑naj=1∑nak=j+1|C［k］C［j］|

=δ|C［2］－C［1］+C［3］－C［1］+…+C［na］－C［1］+C［3］－C［2］+C［4］－C［2］+…+C［na］－C［na－1］|

=δ∑naj=1（2j－na－1）C［j］

=δ∑naj=1（2j－na－1）∑jr=1［1+b（j－r）］pA［r］

=δ∑naj=1∑nah=j（2h－na－1）［1+（h－j）b］pA［j］j=1，2，…，na（21）

綜上，將式（15—21）代入目標(biāo)函數(shù)表達(dá)式F2中，可得

F2=∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θqopt）+αCmax+δTADC+∑j∈Rej

=∑μ－1j=1κ∑μ－1ξ=1［1+b（μ－1－ξ）］pA［ξ］－∑j－1ξ=1［1+b（j－1－ξ）］pA［ξ］+

∑naj=μ+1λ∑j－1ξ=1［1+b（j－1－ξ）］pA［ξ］－∑j－1ξ=1［1+b（μ－1－ξ）］pA［ξ］+∑μ－1j=1u［j］+∑naj=μ+1v［j］+naθ∑naj=1［1+b（μ－1－j）］pA［j］+α∑naj=1［1+b（na－j）］pA［j］+

δ∑naj=1∑nah=j（2h－na－1）［1+（h－j）b］pA［j］+∑j∈Rej

=∑naj=1ψjpA［j］+∑μ－1j=1u［j］+∑naj=μ+1v［j］+∑j∈Rej

其中

ψj=κj（1+b（μ－j－1））+b（μ－j－1）（μ－j）2+λb（na－μ+1）（na－μ）2+naθ［1+b（μ－j－1）］+α（1+b（na－j））+δ∑nah=j（2h－na－1）［1+b（h－j）］j=1，2，…，μ－1λ［2+b（na－j－1）］（na－j）2+α（1+b（na－j））+δ∑nah=j（2h－na－1）［1+b（h－j）］j=μ，…，na

3.2問題求解

若接受工件的個(gè)數(shù)為na，工期取在第μ－1個(gè)位置，即qopt=C［μ－1］時(shí)，在排序π中，若工件Jj在第r個(gè)位置加工，xjr=1；否則xjr=0。則問題：

1|pAj=pjrβj|F2

可以轉(zhuǎn)化成以下指派問題：

min∑nj=1∑nr=1Δnajrxjr

∑nj=1xjr=1r=1，2，…，n∑nr=1xjr=1j=1，2，…，nxjr∈{0，1}

其中

Δjr=ψrpjrβj+ujr=1，2，…，μ－1ψrpjrβjr=μψrpjrβj+vjr=μ+1，…，naejr=na+1，…，n （22）

基于推論和以上所有分析，可以用以下算法來求解該問題。

算法2

第1步計(jì)算初始值F2（0）=∑nj=1ej；

第2步依次令na=1，2，…，n，根據(jù)式（14）和式（22）計(jì)算μ和Δjr，求解每個(gè)指派問題，得到函數(shù)值F2（na）；

第3步計(jì)算最優(yōu)值F*2=min{Fna|na=0，1，2，…，n}。

與定理1類似，有以下定理：

定理2問題1|pAj=pjrβj|F2的復(fù)雜度為O（n4）。

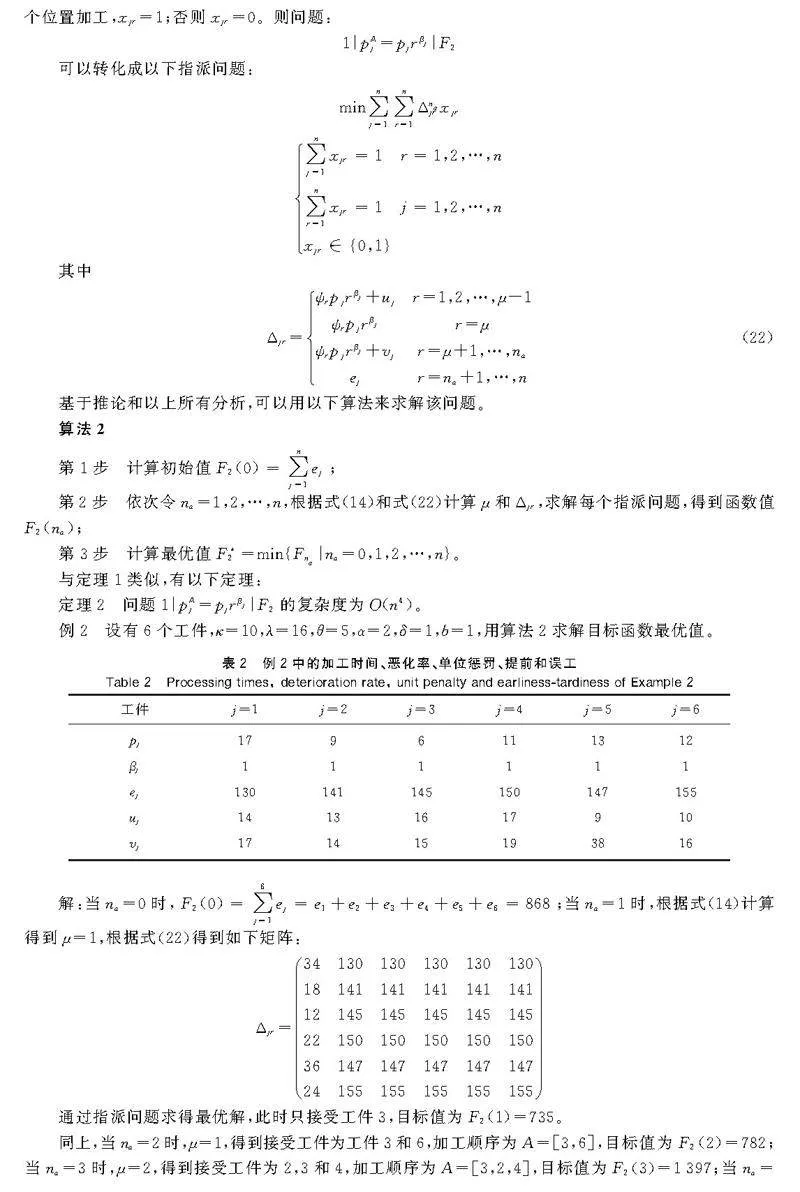
例2設(shè)有6個(gè)工件，κ=10，λ=16，θ=5，α=2，δ=1，b=1，用算法2求解目標(biāo)函數(shù)最優(yōu)值。

解：

當(dāng)na=0時(shí)，F(xiàn)2（0）=∑6j=1ej=e1+e2+e3+e4+e5+e6=868；當(dāng)na=1時(shí)，根據(jù)式（14）計(jì)算得到μ=1，根據(jù)式（22）得到如下矩陣：

Δjr=341301301301301301814114114114114112145145145145145221501501501501503614714714714714724155155155155155

通過指派問題求得最優(yōu)解，此時(shí)只接受工件3，目標(biāo)值為F2（1）=735。

同上，當(dāng)na=2時(shí)，μ=1，得到接受工件為工件3和6，加工順序?yàn)锳=［3，6］，目標(biāo)值為F2（2）=782；當(dāng)na=3時(shí)，μ=2，得到接受工件為2，3和4，加工順序?yàn)锳=［3，2，4］，目標(biāo)值為F2（3）=1397；當(dāng)na=4時(shí)，μ=2，得到接受工件為2，3，4和6，加工順序?yàn)锳=［2，3，4，6］，目標(biāo)值為F2（4）=3088；當(dāng)na=5時(shí)，μ=3，加工順序?yàn)锳=［4，3，2，6，5］，目標(biāo)值為F2（5）=7110；當(dāng)na=6時(shí)，所有工件都被加工，計(jì)算得μ=3，加工順序?yàn)锳=［6，3，4，1，5，2］，目標(biāo)值為F2（6）=14552。

綜上，比較目標(biāo)函數(shù)值，只接受1個(gè)工件3最好，F(xiàn)*2=735。

4DIF指派問題

設(shè)DIF指派問題的目標(biāo)函數(shù)為

F3=∑j∈A（κE［j］+λT［j］+u［j］U［j］+v［j］V［j］+θdj）+αCmax+δTADC+∑j∈Rej

對于DIF指派模型，給定排序π，可以通過極小化以下目標(biāo)函數(shù)來確定最優(yōu)的d*j，因?yàn)槊總€(gè)工件可以分配不同的工期，則可以考慮每個(gè)工件的工期，即考慮第j個(gè)位置的工件的工期d［j］，目標(biāo)函數(shù)值為

f［j］=κmax{0，d［j］－C［j］}+λmax{0，C［j］－d［j］}+u［j］U［j］+v［j］V［j］+θd［j］+αCmax+δTADC

首先給出2個(gè)基本引理。

引理5對于給定排序π，存在一個(gè)最優(yōu)排序，其中d［j］≤C［j］。

證明如果C［j］lt;d［j］，則

f［j］=κ（d［j］－C［j］）+u［j］+θd［j］+αCmax+δTADC

gt;κ（C［j］－C［j］）+u［j］+θC［j］+αCmax+δTADC

因?yàn)榕判蚴墙o定的，Cj已知，所以αCmax+δTADC是定值，將d［j］向左移動(dòng)，直到d［j］=C［j］，此時(shí)d［j］－C［j］=0，u［j］=0；則移動(dòng)之后的目標(biāo)函數(shù)值［j］=θC［j］+αCmax+δTADClt;f［j］，所以C［j］lt;d［j］不是最優(yōu)的，則d［j］≤C［j］成立。

引理6對于給定排序π，如果θ≥λ，則d［j］=0（j=1，2，…，na）；如果θ≤λ，則d［j］=C［j］（j=1，2，…，na）。

證明對于給定排序π，根據(jù)引理5，d［j］≤C［j］，于是有

f［j］=λ（C［j］－d［j］）+v［j］+θd［j］+αCmax+δTADC=λC［j］+v［j］+（θ－λ）d［j］+αCmax+δTADC顯然，如果θ≥λ，則d［j］的值為0。如果θ≤λ，則d［j］=C［j］。

根據(jù)引理5和引理6，可得E［j］=U［j］=0，因而得到以下目標(biāo)函數(shù)表達(dá)式：

F3=λ∑naj=1C［j］+∑naj=1v［j］+αCmax+δTADC+∑j∈Rjejθ≥λθ∑naj=1C［j］+αCmax+δTADC+∑j∈Rjejθ≤λ （23）

將式（3）～（5）代入式（23），整理得

F3=λ∑naj=1（na－j+1）1+na－j2bpA［j］+∑naj=1v［j］+α∑naj=1［1+b（na－j）］pA［j］+δ∑naj=1∑nah=j（2h－na－1）［1+（h－j）b］pA［j］+∑j∈RJejθ≥λθ∑naj=1（na－j+1）1+na－j2bpA［j］+α∑naj=1［1+b（na－j）］pA［j］+δ∑naj=1∑nah=j（2h－na－1）［1+（h－j）b］pA［j］+∑j∈RJejθ≤λ

再將上式進(jìn)一步整理，得到F3=∑naj=1ψjpA［j］+∑naj=1v［j］+∑j∈RJejθ≥λ∑naj=1ψjpA［j］+∑j∈RJejθ≤λ

其中

ψj=λ（na－j+1）1+na－j2b+α（1+b（na－j））+δ∑nah=j（2h－na－1）［1+（h－j）b］θ≥λθ（na－j+1）1+na－j2b+α（1+b（na－j））+δ∑nah=j（2h－na－1）［1+（h－j）b］θ≤λ

4.1問題求解

若接受工件的個(gè)數(shù)為na，則在排序π中，設(shè)工件Jj在第r個(gè)位置加工時(shí)，xjr=1；否則xjr=0。于是問題1|pAj=pjrβj|F3可以轉(zhuǎn)化成以下指派問題：

min∑nj=1∑nj=1Ωnajrxjr

∑nj=1xjr=1r=1，2，…，n∑nr=1xjr=1j=1，2，…，nxjr∈{0，1}

其中，如果θ≥λ，則

Ωjr=ψrpjrβj+vjr=1，2，…，naejr=na+1，na+2，…，n （24）

如果θ≤λ，則

Ωjr=ψrpjrβjr=1，2，…，naejr=na+1，na+2，…，n （25）

對于問題1|pAj=pjrβj|F3，可以用以下算法求解。

算法3

第1步計(jì)算初始值F3（0）=∑nj=1ej；

第2步依次令na=1，2，…，n，根據(jù)式（24—25）計(jì)算Ωjr，求解每個(gè)指派問題，得到函數(shù)值F3（na）；

第3步計(jì)算最優(yōu)值F*3=min{Fna|na=0，1，2，…，n}。

與定理1類似，有以下定理：

定理3問題1|pAj=pjrβj|F3的復(fù)雜度為O（n4）。

例3設(shè)有6個(gè)工件，κ=8，λ=6，θ=5，α=2，δ=1，b=1，用算法3求解目標(biāo)函數(shù)最優(yōu)值。

解：

當(dāng)na=0時(shí)，F(xiàn)3（0）=∑6j=1ej=e1+e2+e3+e4+e5+e6=868；當(dāng)na=1時(shí)，θlt;λ，根據(jù)式（24）和式（25）得到如下矩陣

Ωjr=491301301301301306314114114114114142145145145145145771501501501501502114714714714714784155155155155155

通過指派問題求得最優(yōu)解，此時(shí)只接受工件1，目標(biāo)值為F3（1）=742。

同上，當(dāng)na=2時(shí)，得到接受工件為工件3和5，加工順序?yàn)锳=［5，3］，目標(biāo)值為F3（2）=732；當(dāng)na=3時(shí)，得到接受工件為1，3和5，加工順序?yàn)锳=［3，5，1］，目標(biāo)值為F3（3）=1013；當(dāng)na=4時(shí)，得到接受工件為1，3，4和5，加工順序?yàn)锳=［1，5，3，4］，目標(biāo)值為F3（4）=1636；當(dāng)na=5時(shí)，加工順序?yàn)锳=［4，1，3，2，6］，目標(biāo)值為F3（5）=5034；當(dāng)na=6時(shí)，所有工件都被加工，加工順序?yàn)锳=［6，4，1，2，5，3］，目標(biāo)值為F3（6）=8088。

綜上，比較目標(biāo)函數(shù)值，加工順序?yàn)锳=［5，3］最好，最優(yōu)值為F*3=732。

5結(jié)語

本文研究了帶有拒絕和安裝時(shí)間的單機(jī)排序問題，工件的實(shí)際加工時(shí)間受惡化效應(yīng)的影響，工件在加工之前還帶有安裝時(shí)間，在CON/SLK/DIF指派下，目的為極小化提前、誤工、提前的工件數(shù)量、誤工的工件數(shù)量、工期大小、最大完工時(shí)間、拒絕懲罰及總完工時(shí)間絕對差的加權(quán)和。對于這3個(gè)問題，給出了多項(xiàng)式時(shí)間算法。對于帶有安裝時(shí)間和拒絕工件的模型，今后會(huì)進(jìn)一步研究不同處理機(jī)的問題。

參考文獻(xiàn)：

［1］KRAJCINOVIC D，F(xiàn)ONSEKA G U.The continuous damage theory of brittle materials［J］.J Appl Mech，1981，48（4）：809-824.BROWNE S，YECHIALI U.Scheduling deteriorating jobs on a single processor［J］.Oper Res，1990，38（3）：495-498.

［2］SUN X，GENG X N.Single-machine scheduling with deteriorating effects and machine maintenance［J］.Int J Prod Res，2019，57（10）：3186-3199.

［3］HUANG X，LI G，HUO Y Z，et ak.Single machine scheduling with general time-dependent deterioration，position-dependent learning and past-sequence-dependent setup times［J］.Optim Lett，2013，7（8）：1793-1804.

［4］LIN S S.Due-window assignment scheduling with learning and deterioration effects［J］.J Ind Manag Optim，2022，18（4）：2567-2578.

［5］NIAN H W，MAO Z Z.Single machine scheduling with job rejection，deteriorating effects and deteriorating maintenance activities［J］.Math Prob Eng，2013，2013（1）：389120.

［6］WANG W L.Single-machine due-date assignment scheduling with generalized earliness-tardiness penalties including proportional setup times［J］.J Appl Math Comput，2022，68（2）：1013-1031.

［7］SOROUSH H M.Scheduling in bicriteria single machine systems with past-sequence-dependent setup times and learning effects［J］.J Oper Res Soc，2014，65（7）：1017-1036.

［8］FENG Y F，HU Z H，SI R，et al.Study on due-date assignment scheduling with setup times and general truncated learning effects［J］.Asia Pac J Oper Res，2024，41（1）：2350006.

［9］HUANG X，YIN N，LIU W W，et al.Common due window assignment scheduling with proportional linear deterioration effects［J］.Asia Pac J Oper Res，2020，37（1）：1950031.

［10］LIU W G，WANG X Y，LI L，et al.Due-window assignment scheduling with job-rejection，truncated learning effects and setup times［J］.J Ind Manag Optim，2024，20（1）：313-324.

［11］WANG J B，XU J X，GUO F，et al.Single-machine scheduling problems with job rejection，deterioration effects and past-sequence-dependent setup times［J］.Eng Optimiz，2022，54（3）：471-486.

［12］GERSTL E， MOSHEIOV G.Single machine scheduling problems with generalized due-dates and job-rejection［J］.Int J Prod Res，2017，55（11）：3164-3172.

［13］SHABTAY D，GASPAR N，KASPI M.A survey on offline scheduling with rejection［J］.J Scheduling，2013，16（1）：3-28.

【責(zé)任編輯：溫學(xué)兵】

收稿日期：2023-06-25

基金項(xiàng)目：遼寧省教育廳高校基本科研項(xiàng)目（JYTMS20231698）。

作者簡介：

趙玉芳（1966—），女，遼寧遼陽人，沈陽師范大學(xué)副教授，博士。