晰錯因 明本質 悟方法

陶來舟 吳 躍

安徽省宿城第一中學

荊岫之玉必含纖瑕,驪龍之珠亦有微纇.一道正確(優美)的題目可以讓人賞心悅目,一道錯誤(瑕疵)的題目同樣可以令人遐想萬千.本文中筆者以一道錯題為例,晰錯因、明本質、悟方法.

1 原題呈現

本題是華大新高考聯盟2023屆高三下學期4月教學質量測評(新教材卷)第8題.試題以指數復合函數和余弦函數構造的新函數為載體,考查利用導數研究函數的單調性和恒成立問題,考查學生的邏輯推理和數學運算核心素養.

下面是命題組提供的參考答案:

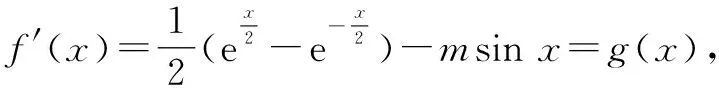
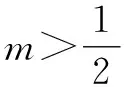
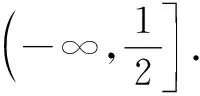
2 晰錯因,以往鑒來

2.1 錯因分析

2.2 答案探究

2.3 題目修正

此題只需稍加修正,便可物盡其用,回歸命題初衷,起到單選題的把關作用,不失為一道難得的好題.

此題答案為選項D,解答過程參考例1,此處省略.

3 明本質,追根溯源

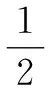
定理(連續函數的局部保號性)設函數f(x)在點x0連續且f(x0)>0(或f(x0)<0),則存在x0的鄰域U,對于任意給定的x∈U,有f(x)>0(或f(x)<0)[1].

例4(2022年新高考全國Ⅱ卷節選)已知函數f(x)=xeax-ex,當x>0時,f(x)<-1,求a的取值范圍.

例3用“端點效應”得到的范圍是必要不充分條件(解答略),例4用“端點效應”得到的范圍是充要條件(解答略).通過以上分析不難發現,“端點效應”只能給解題提供一個大致的思考方向,得到一個必要條件,然后再結合證明判斷是否為充要條件.

4 悟方法,優化教學

試卷講評是高三教學的主流形式,是發展素養的重要土壤.教學時要善于發現問題,啟發學生思考并理解數學本質,引領學生真正喜歡數學.

4.1 激發學生善于思考,做示范者

《普通高中數學新課程標準(2017版2020年修訂)》要求:“通過高中數學課程的學習,樹立學生敢于質疑、善于思考、嚴謹求實的科學精神.”2021年4月,習近平總書記在清華大學考察時強調:“教師要成為“大先生”,做學生為學、為事、為人的示范,促進學生成長為全面發展的人.”[2]善于思考不能流于形式,不是教師在課堂上強調幾遍就敷衍了事;善于思考也不能放手交給學生,因為學生缺少思考經驗只會走入另一誤區.教師應該以身作則做示范者,通過精選試題、練習和精心設計教學環節引導學生去思考.

4.2 高屋建瓴指點迷津,做指導者

高中數學試題紛繁復雜,解法靈活多變,學生的思維更是光怪陸離(天馬行空).要提高教學效率,就需要教師提高個人專業水平.《中學教師專業標準》要求數學教師要以素養為依托,通過實踐,掌握教學所需的基礎知識,提升教書育人的基本能力.以其昏昏,使人昭昭,只會讓學生越來越迷糊.以導數的教學為例,在這一模塊中,存在許多易造成解題思維障礙的問題:①知識間的不等價轉化,如“單調性與導函數的符號”“極值點與導函數的零點”等;②方法間的不等價轉化,如“端點效應”“拉格朗日中值定理”等;③存在很多高等數學知識,如“洛必達法則”“泰勒展開式”等.這些問題在學習和解題時都會給學生帶來不小的困惑,需要教師高屋建瓴指點迷津.打鐵還需自身硬,教師應該自己先搞清楚,做個明白人,才能在教學中“不畏浮云遮望眼”.

4.3 引領學生學會學習,做引路者

高三教學因為教學任務重、教學時間緊,很多都是“滿堂灌”,筆者有時也不得已而為之.“滿堂灌”的教學方式看似完成了教學任務,實際教學效果卻不佳,教師課后的心滿意足、“揚揚得意”也只是一種自我慰藉而已.講過的題目學生仍然不會,這種情況屢見不鮮,究其原因就是學生是被動的“接受者”,課堂上看似學習了很多,但真正“動手操作”的太少.因此,教師要做學生學會學習的引路者,引領學生變被動為主動,在教學中踐行“一題一課”“深度學習”等新的教學理念,讓課堂“慢下來”,讓效率“提上去”.