直線與圓錐曲線題型及解法探究

王昌如

江蘇省宿遷青華中學

直線與圓錐曲線題型靈活多變,難度較大.為提高學生的解題能力,為其數(shù)學水平的提升奠定堅實的基礎(chǔ),教學中應注重相關(guān)題型以及解法的匯總、講解,使學生遇到相關(guān)習題時,能夠迅速破題,增強解答直線與圓錐曲線問題的自信.

1 直線與圓錐曲線位置問題

判斷直線與圓錐曲線的位置關(guān)系,需要將直線和圓錐曲線方程聯(lián)立,轉(zhuǎn)化成一元二次方程,借助Δ進行判斷.同時,還應注重靈活運用向量知識判斷直線與直線的位置關(guān)系.另外,如題目中未提示直線斜率是否存在,解題時還應注重分類討論,不遺漏任何滿足題意的情境,保證考慮問題的全面性.

(1)求k的取值范圍.

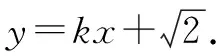
(2)由題意,不妨設(shè)P(x1,y1),Q(x2,y2),則

①

2 直線與圓錐曲線弦長問題

求解圓錐曲線的弦長問題,需通過直線和圓錐曲線方程的聯(lián)立整理成一元二次方程,借助根與系數(shù)的關(guān)系表示出弦長,而后運用已知條件構(gòu)建等式進行求解.另外,若能求出直線和圓錐曲線的交點坐標,則可直接運用公式求出兩點間的距離.

例2已知F為拋物線y2=2px(p>0)的焦點.過點F且和x軸不垂直的直線l和拋物線交于點A(x1,y1),B(x2,y2),且y1y2=-4.

(1)求拋物線的方程.

(2)直線l和y軸交于點D,探究:AB和FD的長度是否相等?若相等,求出直線l的方程;若不等,說明理由.

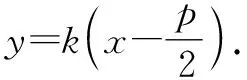
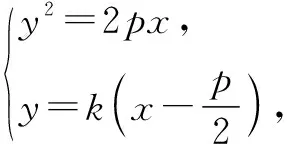
所以拋物線的方程為y2=4x.

(2)由(1)可得直線l的方程為y=k(x-1),將其與拋物線方程y2=4x聯(lián)立,消去y并整理,得

k2x2-2(k2+2)x+k2=0.

而Δ=16(k2+1)>0恒成立,則有

3 直線與圓錐曲線定值問題

求解直線與圓錐曲線的定值問題,應結(jié)合已知條件,通過聯(lián)立直線與圓錐曲線方程,借助一元二次方程根與系數(shù)的關(guān)系,對要求解的定值表達式進行化簡.如表達式中帶有參數(shù),為保證其為定值,應注意將帶參數(shù)的部分消除.

解析：假設(shè)在x軸上存在這樣的一點M(m,0)滿足題意,設(shè)A(x1,y1),B(x2,y2).

當直線AB的斜率存在時,設(shè)對應的直線方程為y=k(x+1).

①

②

將①②代入上式,可得

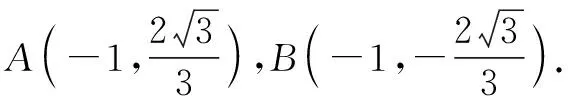
4 直線與圓錐曲線最值問題

解決直線與圓錐曲線的最值問題,通常通過聯(lián)立直線與圓錐曲線的方程,表示出要求解的最值,而后運用函數(shù)或均值不等式知識求解.需要注意的時,在設(shè)出參數(shù)后,應結(jié)合已知條件確定參數(shù)的取值范圍,保證取到最值時符合題設(shè)情境.

例4已知拋物線C:x2=2py(p>0),焦點與準線的距離為2,直線l和拋物線交于A,B兩點,過點A,B分別作拋物線的切線l1,l2.l1和l2交于點M.

(1)拋物線的方程;

(2)若l1⊥l2,求△MAB面積的最小值.

根據(jù)題意,直線l一定存在斜率.設(shè)直線l的方程為y=kx+m.與拋物線方程聯(lián)立,消去y并整理得x2-4kx-4m=0,當Δ=16k2+16m>0時,x1+x2=4k,x1x2=-4m=-4.

所以m=1,則直線l的方程為y=kx+1.

聯(lián)立l1,l2的方程,可求得M(2k,-1).

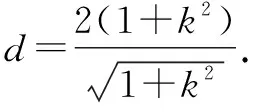
當k=0時,△MAB面積的最小值為4.

直線與圓錐曲線題型具有較好的區(qū)分度.教學中應結(jié)合具體例題,為學生剖析不同題型的解題方法.同時,組織學生開展針對性的訓練活動,鼓勵學生做好解題總結(jié)與反思,把握不同題型的解題規(guī)律以及破題技巧,使其真正攻克這一難點題型.