2023年高考數學全國乙卷第11題的巧思妙變

申光鵬

重慶市江津中學校

直線與圓是平面解析幾何中兩類最簡單的基本圖形,又是初中平面幾何中的基本圖形之一.直線與圓之間的位置關系問題,有效鏈接起初中與高中的相關知識,同時又涵蓋函數與方程、數形結合等基礎數學知識與基本數學思想等,備受各方關注.

特別地,涉及直線與圓的位置關系的綜合應用問題中,有其自身的代數屬性,又有其內涵的幾何特征,實現高考“在知識交匯點處”設計命題的指導精神,同時使得問題的破解思維與技巧策略更加多樣創新,一直是各級各類考試的必考內容和熱點內容之一.

1 真題呈現

高考真題(2023年高考數學全國乙卷文科·11)已知實數x,y滿足x2+y2-4x-2y-4=0,則x-y的最大值是( ).

此題以雙變量所滿足的二元二次方程是一個圓方程來合理創設問題場景,結合雙變量所對應的一次線性代數式的最值求解來設置問題,是平面解析幾何直線與圓的位置關系模塊中比較常見的一類問題,有其特殊的代數屬性與幾何內涵.

在實際解決此類問題時,可以借助解析幾何思維,從直線與圓的位置關系入手,或轉化為幾何圖形的位置關系來處理,或利用參數方程達到目的;也可以借助函數與方程思維,合理引入參數,將問題轉化為相關的一元二次方程問題,利用判別式達到目的.思維視角切入多樣,解題技巧方法紛呈.

2 真題破解

2.1 解析幾何思維

解法1：距離轉化法.

由x2+y2-4x-2y-4=0配方可得(x-2)2+(y-1)2=9,則其幾何意義是以C(2,1)為圓心,半徑為3的圓.

解后反思：根據題設條件中二元二次方程與所求一次代數式的幾何意義,將問題轉化為直線與圓的位置關系問題,借助直線與圓有公共點,通過圓心到直線的距離小于等于半徑來構建對應的不等式,進而得以確定所求一次代數式的最值(或取值范圍).挖掘方程或代數式的幾何意義,由“數”轉“形”,是解決問題的關鍵所在.

解法2：三角換元法.

解后反思：根據題設條件中二元二次方程所對應的幾何意義,借助三角參數方程的構建,合理進行三角換元處理,進而將所求一次代數式表示為三角函數關系式,結合三角恒等變換構建對應的正弦型(或余弦型)函數,利用三角函數的圖象與性質來確定最值(或取值范圍).利用參數方程進行三角換元處理,為問題的進一步分析與解決奠定基礎.

2.2 方程思維

解法3：判別式法.

設x-y=k,則x=y+k,代入x2+y2-4x-2y-4=0,整理可得2y2+(2k-6)y+k2-4k-4=0.

由于以上關于y的二次方程有實數根,則判別式Δ=(2k-6)2-4×2(k2-4k-4)≥0.

整理,可得k2-2k-17≤0.

解后反思：根據所求一次代數式進行整體換元引入參數,代入題設條件中的二元二次方程,將問題轉化為相關的一元二次方程問題,借助一元二次方程有實數根,通過判別式滿足的條件構建不等式,利用解不等式來求解最值(或取值范圍).利用整體思維引入參數,合理消參轉化為相關的一元二次方程,為進一步利用判別式法構建不等式打下基礎.

3 變式拓展

3.1 同階變形

基于高考真題,就一次代數式的最值(最小值或最大值)、取值范圍等來加以合理變式與應用.

變式1已知實數x,y滿足x2+y2-4x-2y-4=0,則x-y的最小值為______.

變式2已知實數x,y滿足x2+y2-4x-2y-4=0,則x-y的取值范圍為______.

以上兩個變式的解題過程,可以直接參照上述高考真題中的解析.

3.2 中階變形

基于高考真題,合理改變一次代數式的系數,也可以對其相應的代數式的最值(最小值或最大值)、取值范圍等問題加以變式與應用.

變式3已知實數x,y滿足x2+y2-4x-2y-4=0,則3x-4y的最大值為______.

解析：由x2+y2-4x-2y-4=0配方,可得到(x-2)2+(y-1)2=9,則其幾何意義是以(2,1)為圓心,半徑為3的圓.

故填答案:17.

3.3 高階變形

基于高考真題,改變所求代數式的結構特征,化一次代數式為相應的一次分式、二次根式等問題,進而求解其對應的最值(最小值或最大值)、取值范圍等,合理變式與應用.

解析：由x2+y2-4x-2y-4=0配方可得到(x-2)2+(y-1)2=9,則其幾何意義是以(2,1)為圓心,半徑為3的圓.

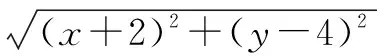
解析：由x2+y2-4x-2y-4=0配方可得到(x-2)2+(y-1)2=9,則其幾何意義是以C(2,1)為圓心,半徑為3的圓.

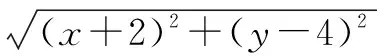
4 教學啟示

4.1 合理交匯,巧妙應用

借助直線與圓的位置關系,以“數”與“形”的巧妙融合,滲透“動”與“靜”的和諧統一,可以從代數思維切入進行合理數學運算,也可以從幾何思維切入進行邏輯推理,實現不同知識點之間的合理交匯與融合,達到知識、能力的綜合與應用的目的,從而使得學生的解題思維更加活躍,解題思路更加開闊,數學知識的掌握更加熟練,問題的破解更加快速有效.

4.2 變式拓展,“一題多變”

通過對問題本質屬性的合理挖掘,全面開拓數學思維,巧妙整合數學知識,結合“一題多解”“一題多思”“一題多變”等探究與應用,實現“一題多得”.基于典型問題的應用,解決并處理一系列的典型數學問題,從而培養發散思維能力與數學解題能力,有助于激發學生學習的積極性、主動性和趣味性,從而全面提高學生的知識水平和思維能力,養成良好的數學品質,培養數學核心素養.