巧借坐標運算,妙解向量問題

陳 晨

廣東省深圳市紅山中學

平面向量自身同時兼備“數”的基本屬性與“形”的結構特征,是銜接代數與幾何的一個紐帶,更是數形結合的典范之一.而利用坐標運算法來處理平面向量的一些相關問題,將相應的平面幾何的“形”的問題加以符號化處理、坐標化表示,轉化為“數”的問題,進行數量化應用與數學運算處理,使得推理應用問題轉化為數學運算問題,可以更加深入地解決一些復雜的綜合性、創新性等平面向量應用問題.

1 參數值的問題

在平面向量中,涉及向量線性關系的系數、線段的比例關系等相關參數值的求解,以及對應參數的代數關系式的求解問題,經常可以借助平面直角坐標系的構建,利用坐標運算法來進行數學運算與邏輯推理等.

圖1

分析：根據平面幾何圖形,合理構建平面直角坐標系,將平面圖形中的線段長度與角度關系轉化為對應的點的坐標,利用坐標運算來確定相應的向量,結合向量的坐標運算構建對應參數的關系式,進而確定所求關系式的值.

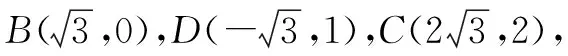
圖2

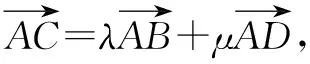
故選擇答案:D.

點評：解決此類問題的方法比較多,可以通過“數”的思維來應用,也可以通過“形”的特征來分析.而利用坐標運算法解決平面向量中對應參數值的求解問題時,關鍵是將直觀形象的平面幾何圖形放置于對應的平面直角坐標系中,借助相應的坐標表示,化邏輯推理為數學運算,借助坐標運算來分析與求解.

2 向量模的問題

在平面向量中,涉及向量的模或模的取值范圍(或最值)的求解問題,經常可以借助平面直角坐標系的構建,合理引入向量的坐標,進而利用坐標運算法來進行數學運算與邏輯推理等.

例2已知平面向量a,b,c滿足|c|=1,且滿足a·c=2,b·c=1,則|a+b|的最小值為______.

分析：根據題設條件,通過合理構建對應的平面直角坐標系,并引入向量a,b的坐標,結合向量的數量積公式確定相關參數的值,利用向量模的公式構建對應的關系式以及利用函數的基本性質來確定相應的最值問題.

解析：依題建立相應的平面直角坐標系,不失一般性,不妨設c=(1,0),a=(x,y),b=(m,n),其中x,y,m,n∈R.

結合條件a·c=2,b·c=1,利用向量數量積的坐標公式,可得a·c=x=2,b·c=m=1.

因為a+b=(x+m,y+n),所以|a+b|2=(x+m)2+(y+n)2=9+(y+n)2≥9,當且僅當y+n=0時,等號成立.

所以|a+b|≥3,即|a+b|的最小值為3.

故填答案:3.

點評：借助適當的平面直角坐標系的構建并引入向量的坐標,為和向量的模合理構建對應的函數關系式,進而結合參數之間的關系與表示,利用函數的基本性質來分析與轉化.通過代數思維中的坐標運算來處理此類向量模的相關問題,借助純粹的代數運算即可達到目的,目標明確.

3 數量積的問題

在平面向量中,涉及平面向量的數量積以及數量積的線性關系式等的求解、取值范圍(或最值)的確定問題,經常可以借助平面直角坐標系的構建,利用坐標運算法來進行數學運算與邏輯推理等.

分析：根據平面向量自身“數”的基本屬性,通過數學運算,借助坐標法來轉化與應用,巧妙引入點或夾角等參數,通過點的坐標、向量的坐標及其對應的運算、數量積公式等,綜合三角函數等其他知識來應用.

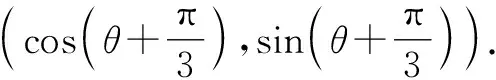
故選擇答案:A.

點評：通過題目條件合理引入對應的點或夾角等參數,進而利用平面向量數量積的坐標公式,將已知條件轉化為涉及參數的代數關系式,結合函數的圖象與性質、三角函數的有界性或不等式的基本性質等來確定對應關系式的最值問題.此類問題利用代數思維往往更加方便,利用相應的數學運算即可得到最終結論.

4 創新應用問題

創新意識與創新應用是新時代的一個主旋律.在平面向量中,涉及平面向量問題的創新應用也是一大主陣地,挖掘創新本質,合理構建平面直角坐標系,坐標運算法有時也是解決向量創新應用問題的一個不錯的選擇.

分析：根據題目條件,巧妙建立相應的平面直角坐標系,引入對應向量的坐標參數,利用向量投影的幾何意義并結合題設條件確定相關向量c的坐標關系,進而利用平面向量的坐標運算、向量模的公式等構建對應的函數解析式,結合創新定義并利用函數的基本性質加以分步處理,分層解決.

解析：依題建立相應的平面直角坐標系xOy,結合a⊥b,不失一般性,可設平面向量a=(a,0),b=(0,b),a,b∈R.

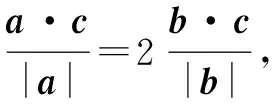
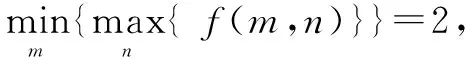
故填答案:2.

點評：通過建系,利用坐標運算法,合理把握創新應用問題的實質,是處理此類平面向量中創新問題比較常用的一種通技通法.

借助坐標運算法來解決平面向量的綜合應用問題,通過點、向量等的坐標化處理,由“形”轉化為“數”,利用代數思維來解決平面向量中的“數”或“形”的相關問題,避免變幻莫測的直觀圖形和繁雜的邏輯推理等,實現平面幾何問題的代數化,由變化多端的平面向量應用問題轉化為對應坐標的代數運算問題,方向性強,思維單一,技巧易懂,方法靈活,值得借鑒與推廣.