關注應用 提升素養
——對基本不等式教學的幾點建議

陳 霞

山東省濟南市萊蕪第一中學

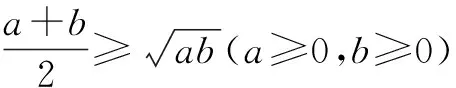
1 巧借錯誤,形成正確認識

為了讓學生能夠靈活應用基本不等式這一知識點解決問題,首先要讓學生形成正確的認識.在基本不等式的教學過程中,教師會重點強調“一正、二定、三相等”這一重要的適用條件,但是學生在具體應用中還是會發生遺忘,從而引發錯誤.為了減少或避免遺忘,教師不妨主動“示錯”,讓學生在“糾錯”的過程中形成正確的、深刻的認識,以此提高解題準確率.

案例1判斷以下題目的解答過程是否正確?若有錯誤,請寫出糾正過程.

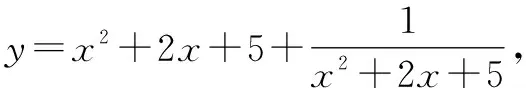
解:因為x2+2x+5>0,則由基本不等式可得y≥2,所以函數的最小值為2.

問題給出后,讓學生獨立糾錯,教師巡視,并進行個別點撥,然后呈現學生的糾錯過程.

師:誰來說一說,問題(1)的解題過程正確嗎?為什么?

生1:問題(1)的解答是錯誤的,在應用基本不等式解決問題時,忽視了“相等”這一條件.若想讓等號成立,則需x=2y和x=y同時成立,顯然這是不可能的,所以該解法是錯誤的.

師:分析得非常好!你是如何求解的呢?

生1的解題過程給出后,教師讓學生點評,以此進一步深化對基本不等式的理解.學生理解并掌握問題(1)后,再繼續呈現問題(2)的分析過程.

師:誰來說一說問題(2)?

師:具體說一說,你是如何求解的.

師:很好,運用基本不等式時一定要注意等號成立的條件.雖然利用基本不等式求最值是一種重要的解題方法,但是這并不代表所有的求最值問題都可以用基本不等式來求解.解題時切勿盲目套用,要充分考慮公式的適用條件.

在實際教學中,有些易錯點、重難點,教師是反復講、重復練,但是解題效果依然難以達到預期.基于此,教師不妨主動呈現錯誤,讓學生在錯誤中思考,在思考中深化,以此有效規避或減少錯誤的發生,培養學生的批判性思維能力.

2 巧借應用,促進知識深化

基本不等式在函數、不等式中有著重要的應用,是高考中極其重要的知識點.引導學生運用所學知識解決問題是數學教學的落腳點,也是提高學生學習能力,發展學生數學素養的必經之路.基本不等式的用法比較靈活,教師有必要引導學生從不同角度出發,思考不同的解決方法,讓學生學會順用、逆用、靈活用,以此提高學生解決問題的能力.另外,教學中,教師應重視呈現學生的思維過程,以此通過對比分析發現不同解決的策略,提高學生數學應用水平.

分析：本題若直接從結論出發,很難看到基本不等式的“身影”,因為在條件“a+b=1”的作用下,基本不等式被隱藏了起來,學生對“a+b=1”這一條件的處理直接影響著解題效果.本題求解時,不妨將“1”化身為“a+b”,由此可見基本不等式的“真面目”,從而順利地解決問題.

解題時,讓學生獨立解決,并鼓勵學生應用不同的方法證明.現將學生的證法總結如下:

教師呈現學生的解題過程,并讓學生進行歸納整理,然后給出如下變式問題.

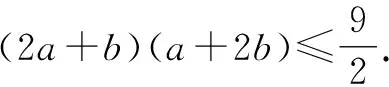
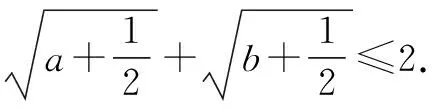
在日常教學中,適度地運用變式訓練,不僅可以幫助學生鞏固知識、強化技能,而且可以凸顯問題的本質,提升學生舉一反三的能力.其實,基本不等式中蘊含著豐富的數學思想方法,如逆向思維、轉化與化歸、數形結合等.在日常教學中,教師應創造機會讓學生總結歸納,以此感悟思想、提煉方法,提高學生的思維品質,提升學生解題能力.

3 聯系實際,促進知識升華

在課堂教學中,教師應提供機會讓學生利用所學知識去解決實際問題,以此激發學生學習的動機,提高學生學習興趣.“學以致用”既是數學教學的出發點,也是數學教學的落腳點,教學中要引入一些學生熟悉的、感興趣的生活實例,以此引發學生情感共鳴,激發學生學習積極性.

案例3小明和小剛每個月都會相約到一家超市購買兩次大米,他們采用了不同的購買方式,小剛每次購買10 kg大米,小明每次購買10元大米.假設大米的價格是有波動的,第一次購買時的價格為x元/kg,第二次購買時的價格為y元/kg,試問以上兩種購買方式,哪種更劃算?

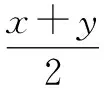
這樣從學生熟悉的生活情境出發,不僅可以調動學生參與的積極性,而且可以培養學生的應用意識.其實,生活中有許多關于最值問題都可以應用基本不等式來解決,教師要合理引入,以此讓學生全面、系統地理解基本不等式.