基于“四個(gè)理解”的“冪函數(shù)”教學(xué)設(shè)計(jì)

王立波

哈爾濱師范大學(xué)教師教育學(xué)院

章建躍博士在“中小學(xué)數(shù)學(xué)課程核心內(nèi)容及其教學(xué)的研究”中提出:改進(jìn)課堂教學(xué)需基于理解數(shù)學(xué)、理解學(xué)生、理解技術(shù)、理解教學(xué)實(shí)施[1].本文中在把握數(shù)學(xué)本質(zhì)的同時(shí),立足數(shù)學(xué)核心素養(yǎng)并基于“四個(gè)理解”對(duì)“冪函數(shù)”一課進(jìn)行教學(xué)設(shè)計(jì).

1 理解數(shù)學(xué),設(shè)定教學(xué)目標(biāo)

確定教學(xué)目標(biāo)的方向舵是以理解數(shù)學(xué)為前提的.在冪函數(shù)的教學(xué)中,教師可以把重心放在對(duì)章節(jié)結(jié)構(gòu)的把握和對(duì)內(nèi)容的清晰認(rèn)識(shí)上,以便建立起研究冪函數(shù)的一般思路:定義—圖象與性質(zhì)—應(yīng)用.冪函數(shù)也是學(xué)生進(jìn)入高中階段學(xué)習(xí)的第一類具體函數(shù),對(duì)后面指數(shù)函數(shù)、對(duì)數(shù)函數(shù)、三角函數(shù)等的學(xué)習(xí)起到領(lǐng)頭羊的作用,從而可以實(shí)現(xiàn)數(shù)學(xué)知識(shí)的自然延拓.

在“冪函數(shù)”的教學(xué)中,教師也要注重對(duì)上、下位知識(shí)的把握.冪函數(shù)概念形成的上位知識(shí)是學(xué)生實(shí)現(xiàn)從“變量說”到“對(duì)應(yīng)說”的一次思維跨越,學(xué)生可以從具體的實(shí)際情境中抽象出以前接觸過的幾種函數(shù)模型;冪函數(shù)的下位知識(shí)是學(xué)生能根據(jù)抽象出的幾種函數(shù)模型進(jìn)行歸納概括,并將前面學(xué)習(xí)到的函數(shù)的具體性質(zhì)(單調(diào)性、奇偶性等)引申到冪函數(shù)的研究中,借助函數(shù)圖象去高度概括和抽象.同時(shí),對(duì)于高一的學(xué)生來說,他們?cè)诔踔幸呀?jīng)學(xué)習(xí)過幾種函數(shù)模型,并且已經(jīng)掌握了函數(shù)的概念和性質(zhì).

基于此,本節(jié)課的教學(xué)目標(biāo)設(shè)定為:根據(jù)定義正確判斷冪函數(shù),會(huì)畫簡(jiǎn)單冪函數(shù)的圖象;經(jīng)歷作圖、觀察,能歸納總結(jié)出冪函數(shù)的性質(zhì),進(jìn)一步滲透數(shù)形結(jié)合思想,培養(yǎng)抽象概括能力;通過生活實(shí)例引入冪函數(shù)的概念,體會(huì)數(shù)學(xué)在實(shí)際生活中的應(yīng)用;利用幾何畫板了解冪函數(shù)圖象的變化規(guī)律.

2 理解學(xué)生,明晰教學(xué)重難點(diǎn)

在教學(xué)中,學(xué)生是課堂的主體,教師只是起著一定的引導(dǎo)作用.因此,教師要把學(xué)生看成一個(gè)個(gè)有思想的個(gè)體,不能對(duì)學(xué)生進(jìn)行“填鴨式”教育.對(duì)于數(shù)學(xué)教學(xué),要看學(xué)生的知識(shí)儲(chǔ)備是否充足,思維上對(duì)知識(shí)的理解是否有障礙,這就要求數(shù)學(xué)教師需要有一定的知識(shí)儲(chǔ)備,教學(xué)生用數(shù)學(xué)知識(shí)去解決問題.

教學(xué)設(shè)計(jì)時(shí),首先要了解學(xué)生已具備的知識(shí)結(jié)構(gòu),然后再通過新課來獲得新知識(shí),在后續(xù)的學(xué)習(xí)中不斷強(qiáng)化知識(shí)水平,從而提高學(xué)生的知識(shí)儲(chǔ)備[2].

因此,確定本節(jié)課的教學(xué)重點(diǎn)是歸納總結(jié)出冪函數(shù)的概念和性質(zhì).通過對(duì)五個(gè)簡(jiǎn)單冪函數(shù)的研究,在研究過程中做到對(duì)知識(shí)系統(tǒng)的擴(kuò)充,從而確定研究基本初等函數(shù)的思路,為后續(xù)函數(shù)的學(xué)習(xí)奠定基礎(chǔ).教學(xué)難點(diǎn)在于借助五個(gè)函數(shù)圖象來研究簡(jiǎn)單冪函數(shù)的性質(zhì),歸納總結(jié)出指數(shù)α對(duì)一般冪函數(shù)的圖象以及性質(zhì)的影響.

3 理解技術(shù),升華教學(xué)內(nèi)容

高中數(shù)學(xué)是比較抽象的,可以將信息技術(shù)融入到教學(xué)的過程中,使其成為教學(xué)的一種工具,并與數(shù)學(xué)學(xué)習(xí)相輔相成,幫助學(xué)生更好地吸收消化所學(xué)內(nèi)容.教師要在“理解數(shù)學(xué)”的基礎(chǔ)上“理解技術(shù)”,通過借助一些數(shù)學(xué)軟件來輔助教學(xué),以很好地培養(yǎng)學(xué)生的數(shù)學(xué)抽象、直觀想象等數(shù)學(xué)學(xué)科核心素養(yǎng).當(dāng)數(shù)學(xué)“不能動(dòng)”的時(shí)候,借助信息技術(shù)輔助教學(xué),可以讓學(xué)生非常直觀地感受到、理解到、想象到,從而讓這些知識(shí)躍然紙上,活靈活現(xiàn),更利于學(xué)生接受.借助信息技術(shù)來輔助教學(xué),能使死板抽象的知識(shí)成為發(fā)展學(xué)生直觀想象素養(yǎng)的點(diǎn)睛之筆.

對(duì)于“冪函數(shù)”這節(jié)課,教師可以借助幾何畫板等軟件來輔助教學(xué),利用信息技術(shù)來解決學(xué)生的困惑,通過動(dòng)態(tài)的函數(shù)圖象來提高學(xué)生對(duì)函數(shù)圖象的認(rèn)識(shí),進(jìn)而得到冪函數(shù)的性質(zhì),化抽象為具體,從而有效地促進(jìn)教學(xué),提高教學(xué)效率.

4 理解教學(xué),精設(shè)教學(xué)過程

4.1 創(chuàng)設(shè)情境,講授新知

我們知道,函數(shù)可以來刻畫現(xiàn)實(shí)世界中的實(shí)際問題,先來看幾個(gè)實(shí)例:

(1)在疫情期間,某學(xué)校以1元/包的價(jià)格購買了w包口罩,那么學(xué)校需要支付的金額p是多少?

(2)某市建造的方艙醫(yī)院的俯視圖為正方形,其邊長為a,那么該正方形的面積S是多少?

(3)韓紅為山區(qū)孩子捐贈(zèng)了很多文具,其中粉筆盒(正方體)的棱長為b,那么粉筆盒的體積V是多少?

(4)魔方一面的面積為S,那么這個(gè)魔方的棱長c是多少?

(5)如果醫(yī)院的救護(hù)車ts內(nèi)行進(jìn)了1 km,那么救護(hù)車的平均速度v是多少?

師生活動(dòng):從學(xué)生熟悉的、關(guān)心的生活實(shí)例出發(fā),充分激發(fā)學(xué)生的好奇心.學(xué)生思考后得到相應(yīng)的關(guān)系式.

4.2 概念構(gòu)建,突破難點(diǎn)

問題1由以上實(shí)例得到的這五個(gè)關(guān)系式,它們是函數(shù)關(guān)系嗎?并說明理由.

師生活動(dòng):通過觀察思考,學(xué)生能得出這幾個(gè)式子是函數(shù)關(guān)系.在相應(yīng)的取值范圍內(nèi),對(duì)于每一個(gè)確定的w,經(jīng)過對(duì)應(yīng)關(guān)系后,都有唯一確定的p與之對(duì)應(yīng).接著引導(dǎo)學(xué)生將自變量用字母x來代替,因變量用字母y來代替.

問題2觀察這五個(gè)函數(shù)的解析式,從自變量、函數(shù)值和解析式的結(jié)構(gòu)特征來看,它們有什么共同特征?請(qǐng)同學(xué)們按小組討論.

師生活動(dòng):通過觀察并討論,學(xué)生歸納出共同特征——解析式都是冪的形式,其中底數(shù)為自變量,指數(shù)是常數(shù),冪值前面的系數(shù)都是1.接著,在教師的點(diǎn)撥下,將它們表示成y=xa的形式,并命名為“冪函數(shù)”,其中x是自變量,α是常數(shù).

問題3判斷下列函數(shù)是否為冪函數(shù)?如果不是,說明理由.

(1)y=x-2.1; (2)y=3x3;

(3)y=3x; (4)y=x2+x.

師生活動(dòng):學(xué)生獨(dú)立完成之后展示交流,教師規(guī)范注意事項(xiàng).

y=x-2.1是冪函數(shù),冪的指數(shù)除了取整數(shù)外,還可以取其他實(shí)數(shù).

y=3x3不是冪函數(shù),xa前面的系數(shù)應(yīng)該是1.

y=3x不是冪函數(shù),冪函數(shù)的底數(shù)只能是自變量x,指數(shù)應(yīng)該是常數(shù).

y=x2+x不是冪函數(shù),冪函數(shù)只有一項(xiàng).

4.3 類比探索,整體認(rèn)知

問題4在初中我們已經(jīng)學(xué)習(xí)過幾種函數(shù),結(jié)合以往學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),知道了一個(gè)函數(shù)的定義后,接下來研究什么呢?

追問1:在研究函數(shù)的圖象和性質(zhì)之前,應(yīng)先明確什么?

追問2:作出函數(shù)圖象以后,可以研究哪些內(nèi)容?

師生活動(dòng):教師幻燈片動(dòng)態(tài)展示研究路徑,如圖1.

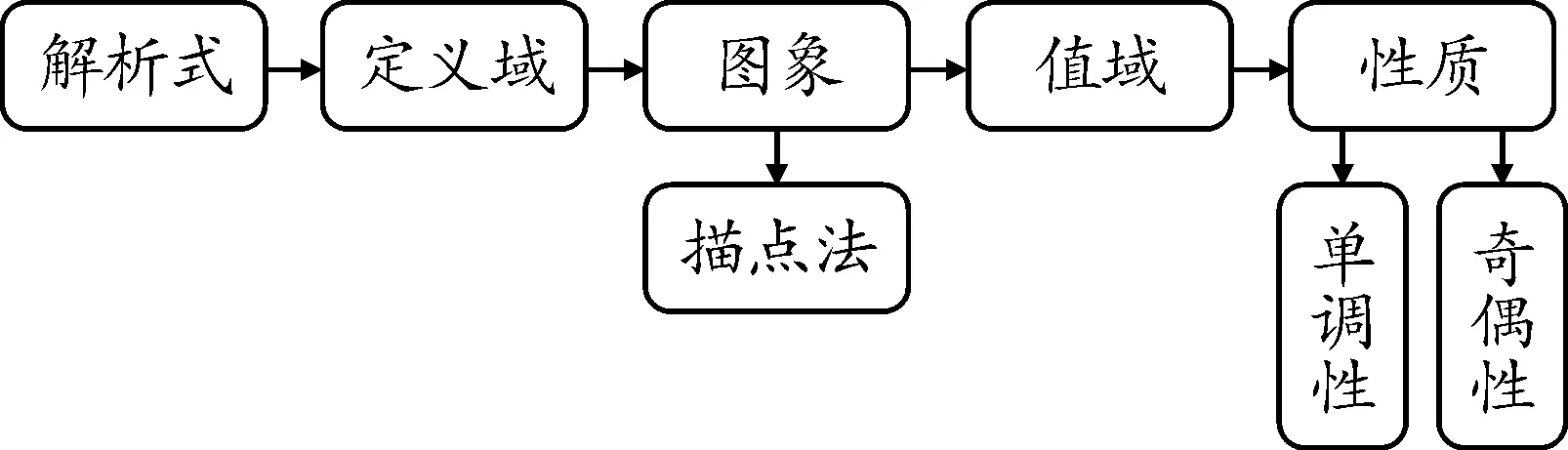
圖1

利用幾何畫板畫出學(xué)生熟悉的三個(gè)函數(shù)的圖象,如圖2.請(qǐng)學(xué)生填寫表1.

表1

圖2

問題6如何畫出y=x3的圖象?

師生活動(dòng):學(xué)生能說出畫函數(shù)圖象的一般思路是列表、描點(diǎn)、連線.在教師的點(diǎn)撥下,學(xué)生能說出先畫出它在[0,+∞)上的圖象,再利用奇函數(shù)的圖象對(duì)稱性畫出整個(gè)定義域上的函數(shù)圖象.因此,作圖時(shí)可先根據(jù)解析式初步判斷函數(shù)的性質(zhì),進(jìn)而簡(jiǎn)化作圖過程.

對(duì)于y=x3而言,可以得出它的定義域?yàn)镽,是一個(gè)奇函數(shù),圖象關(guān)于原點(diǎn)對(duì)稱.

因此,可以先畫出它在[0,+∞)上的圖象,然后根據(jù)奇偶性畫出它在(-∞,0]上的圖象.根據(jù)圖象可以看出,它的值域?yàn)镽,是在R上單調(diào)遞增.

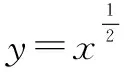
問題7利用幾何畫板,把五個(gè)函數(shù)圖象放在同一個(gè)平面直角坐標(biāo)系中,如圖3.觀察這五個(gè)函數(shù)圖象,請(qǐng)大家填寫表2,然后思考它們有哪些共同的性質(zhì)?有哪些不同點(diǎn)?

圖3

師生活動(dòng):通過觀察,學(xué)生發(fā)現(xiàn)五個(gè)圖象都經(jīng)過點(diǎn)(1,1),第四象限沒有圖象.學(xué)生能答出冪函數(shù)是形如y=xα的函數(shù),當(dāng)自變量x取1時(shí),1的任何次方都是1;當(dāng)x取正數(shù)時(shí),不論α為何數(shù),對(duì)應(yīng)的函數(shù)值都是大于0的數(shù),所以第四象限沒有圖象.函數(shù)y=x,y=x3,y=x-1是奇函數(shù),函數(shù)y=x2是偶函數(shù).

問題8是否可以對(duì)常數(shù)α進(jìn)行分類?怎么分?

師生活動(dòng):學(xué)生先獨(dú)立思考,再分小組討論,最后師生共同總結(jié).

當(dāng)α為奇數(shù)時(shí),函數(shù)y=xα是奇函數(shù);當(dāng)α為偶數(shù)時(shí),函數(shù)y=xα是偶函數(shù).

4.4 課時(shí)小結(jié),知識(shí)建構(gòu)

問題9本節(jié)課你學(xué)到了哪些知識(shí)?獲得了怎樣的研究問題的經(jīng)驗(yàn)?(學(xué)生自主總結(jié)后回答.)

4.5 布置作業(yè),回歸拓展

必做題:教材第91頁的練習(xí).

拓展題:自主探究一般冪函數(shù)是否具有上述性質(zhì),并寫出研究報(bào)告.

在新課程改革的背景下,教師“理解數(shù)學(xué)”,有利于把握整節(jié)課的教學(xué)脈絡(luò),完善學(xué)生的認(rèn)知結(jié)構(gòu);教師“理解學(xué)生”,關(guān)注學(xué)生的最近發(fā)展區(qū),有利于選擇恰當(dāng)?shù)慕虒W(xué)方法;教師“理解技術(shù)”,借助信息技術(shù)輔助教學(xué),有利于學(xué)生認(rèn)清知識(shí)的本質(zhì);教師“理解教學(xué)”,有助于實(shí)現(xiàn)教與學(xué)的內(nèi)在統(tǒng)一.基于“四個(gè)理解”進(jìn)行教學(xué)設(shè)計(jì),是有效落實(shí)數(shù)學(xué)核心素養(yǎng)的關(guān)鍵所在.