直覺引領(lǐng) 運(yùn)算探究 模型回歸
——以2023年全國乙卷(理科)第20題為例

孫愛文 張 凡

江蘇省沭陽高級中學(xué)

1 試題呈現(xiàn)

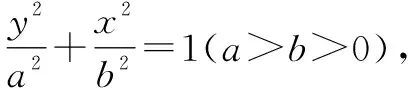
(1)求曲線C的方程;

(2)過點(diǎn)(-2,3)的直線交曲線C于P,Q兩點(diǎn),直線AP,AQ與y軸交于M,N兩點(diǎn),求證:MN的中點(diǎn)為定點(diǎn).

2 試題分析

本題第(1)問為常規(guī)的求曲線方程問題.第(2)問考查定點(diǎn)問題,這是近幾年最為風(fēng)靡的齊次化聯(lián)立模型,背景是極點(diǎn)、極線,考查了解析幾何的基本思想和基本方法,對學(xué)生運(yùn)算能力的要求很高,體現(xiàn)了邏輯推理、數(shù)學(xué)建模、數(shù)學(xué)運(yùn)算等核心素養(yǎng).現(xiàn)給出第(2)問的解題思維導(dǎo)圖,如圖1所示.

圖1

3 試題詳解

思路1：從必要條件出發(fā),先猜后證.

解法1：設(shè)P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4),T(-2,3).

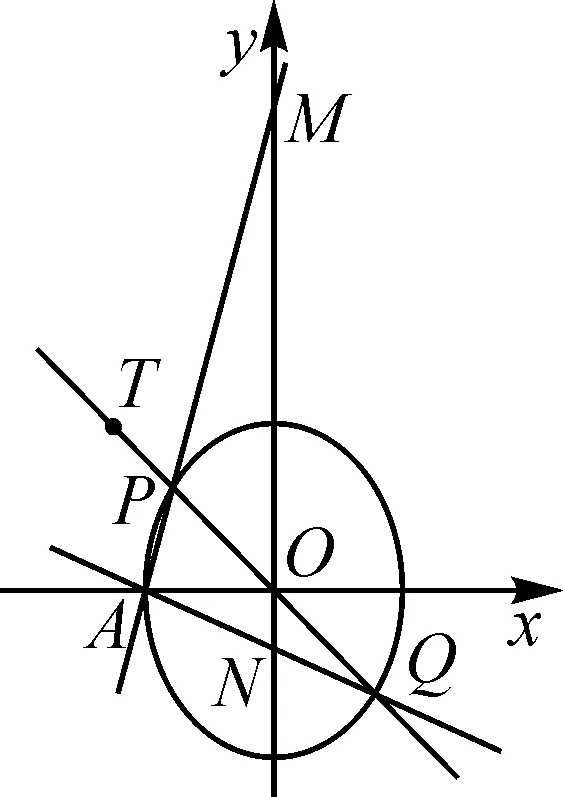
圖2

或者極限分析,PQ無限趨近于一點(diǎn)時(shí),PQ直線方程為y=3,此時(shí)M(0,3),N(0,3)故MN的中點(diǎn)為定點(diǎn)為(0,3).再作如下證明:

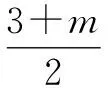
聯(lián)立直線AM與橢圓方程,得(m2+6m+18)x2+4(3+m)2x+4m2+24m=0.

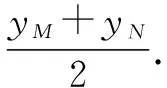
解法2：設(shè)線法+韋達(dá)定理.

設(shè)lPQ:y=k(x+2)+3,P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4),則

對于lAP和lAQ,令x=0,可得

①

故MN的中點(diǎn)為定點(diǎn)(0,3).

解法2的優(yōu)化:整體代換.

設(shè)lPQ:y=k(x+2)+3,P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4).

聯(lián)立橢圓與直線PQ方程,得(4k2+9)(x+2)2+24k(x+2)=0(Δ>0).

同解法2,利用韋達(dá)定理代入計(jì)算得MN的中點(diǎn)為定點(diǎn)(0,3).

把x+2看成整體以后,運(yùn)算大大簡化,這種簡化的思想也是處理解析幾何繁瑣運(yùn)算的常見思路.從代數(shù)的角度來看它是整體代換,從幾何角度來看它的本質(zhì)就是平移坐標(biāo)系.

思路3：平移坐標(biāo)系.

思路4：設(shè)線齊次化,將直線PQ方程代換.

對于lAP與lAQ,令x=0,可得MN的中點(diǎn)坐標(biāo)為(0,k1+k2).

點(diǎn)評：利用平移、齊次化手段來解圓錐曲線中有關(guān)斜率之和或之積問題的理論基礎(chǔ)是平移坐標(biāo)系只是改變了點(diǎn)、曲線在坐標(biāo)系中的位置,其幾何屬性如線段長度、直線斜率,直線間夾角都不會(huì)改變,但并不是所有圓錐曲線都適合平移、齊次化,只有涉及或者可以轉(zhuǎn)化成兩直線斜率之和、之積的問題才適合.方法雖好,但要慎用!

思路5：斜率同構(gòu)或向量周構(gòu).

解法5：斜率同構(gòu).

設(shè)lAP:y=k(x+2),lPQ:y=t(x+2)+3,P(x1,y1),Q(x2,y2),M(0,y3),N(0,y4),且y3=2k.聯(lián)立直線AP與橢圓方程,得(4k2+9)x2+16k2x+16k2-36=0(Δ>0),求出點(diǎn)P坐標(biāo)再代入直線PQ方程,得12k2-36k+36t+27=0.設(shè)kAQ=k′,同理12k′2-36k′+36t+27=0,則k和k′是二次方程12x2-36x+36t+27=0的兩個(gè)根,所以k+k′=3.故MN的中點(diǎn)為定點(diǎn)(0,3).

解法6：向量同構(gòu).

點(diǎn)評：思路5的兩種解法同樣是證明斜率之和為定值,卻沒有用到齊次化的方法,技巧性相對于解法4小很多,相當(dāng)于尋找斜率滿足的二次方程,也有同法可究.計(jì)算量也比前面幾個(gè)解法小很多.

思路6：設(shè)點(diǎn),利用點(diǎn)差法建立點(diǎn)M,N與點(diǎn)P,Q之間的關(guān)系.

解法7：設(shè)點(diǎn)法之點(diǎn)代法.

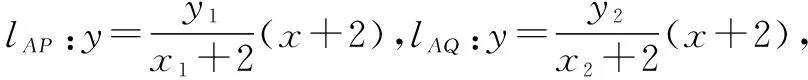
點(diǎn)評：解法7完全用點(diǎn)的坐標(biāo)串聯(lián),設(shè)出點(diǎn)的坐標(biāo)以后,尋求其滿足的代數(shù)方程,通過代數(shù)方程的整體代換來實(shí)現(xiàn)定值的計(jì)算.

解法8：定比點(diǎn)差法.

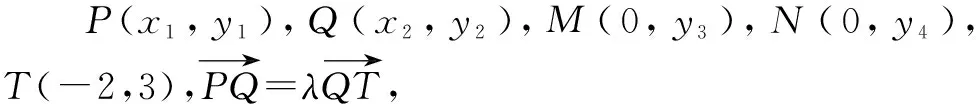
思路7：極坐標(biāo)設(shè)點(diǎn).

解法9：角參法.

于是可得lPQ:2y(t1+t2)+3x(1-t1t2)=6(t1t2+1),代入點(diǎn)P坐標(biāo),得t1+t2=2.

思路8：曲線系法.

解法10：設(shè)lAP:x-my+2=0,lAQ:x-ny+2=0,lPQ:kx-y+2k+3=0,又橢圓在點(diǎn)A處的切線為x+2=0,因此過A,P,Q的二次曲線系為

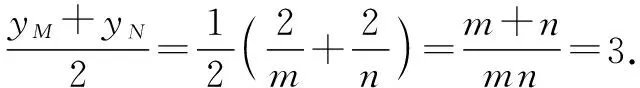
解法11：極點(diǎn)極線法.

下附練習(xí),供讀者參考使用.

(1)求橢圓M的方程;

(2)直線l與橢圓M交于C,D兩個(gè)不同的點(diǎn)(異于A,B),過C作x軸的垂線分別交直線AB,AD于點(diǎn)P,Q,當(dāng)P是CQ中點(diǎn)時(shí),證明:直線l過定點(diǎn).

基于上述對試題的探討研究,作出以下推廣:

解析幾何的相關(guān)問題對學(xué)生的基礎(chǔ)能力、運(yùn)算求解能力及應(yīng)變能力要求較高,需要學(xué)生在平時(shí)的學(xué)習(xí)中學(xué)會(huì)歸納整理知識,建立各知識點(diǎn)之間的關(guān)系網(wǎng),同時(shí)注重思維拓展,一題多解,提升能力.