學(xué)科能力導(dǎo)向下數(shù)學(xué)課堂提問水平研究
——以某專家型教師三節(jié)連續(xù)常態(tài)課為例

北京師范大學(xué) 虞佳晨 陳智豪 程 藝 綦春霞

隨著教育改革的深入，數(shù)學(xué)課程目標(biāo)從知識(shí)技能培養(yǎng)轉(zhuǎn)為學(xué)科能力的發(fā)展。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》提出數(shù)學(xué)學(xué)科的核心素養(yǎng)。數(shù)學(xué)學(xué)科素養(yǎng)是學(xué)生在學(xué)習(xí)數(shù)學(xué)的過程中所具有的關(guān)鍵能力和必備品格。數(shù)學(xué)的關(guān)鍵能力又是如何在數(shù)學(xué)學(xué)科中體現(xiàn)出來的呢？因此，本研究選擇對北京某中學(xué)8年級(jí)的一位專家教師連續(xù)三節(jié)常態(tài)課（其中第一課時(shí)為軸對稱，第二、三課時(shí)為線段垂直平分線的性質(zhì)）進(jìn)行分析，以描述教師常態(tài)教學(xué)中能力導(dǎo)向課的特點(diǎn)，為體現(xiàn)新課標(biāo)的課堂教學(xué)提供一定的借鑒。

一、體現(xiàn)素養(yǎng)的數(shù)學(xué)能力框架

參照布魯姆認(rèn)知領(lǐng)域分類層次、課標(biāo)能力要求以及以往的研究，構(gòu)建了數(shù)學(xué)能力的3×3框架。根據(jù)數(shù)學(xué)學(xué)科認(rèn)識(shí)活動(dòng)的不同層面，對學(xué)科3×3能力層級(jí)模型，進(jìn)行如下劃分：3個(gè)能力分級(jí)為學(xué)習(xí)理解（A）、應(yīng)用實(shí)踐（B）、遷移創(chuàng)新（O），每個(gè)能力層級(jí)包含3個(gè)子能力要素；學(xué)習(xí)理解（A）包含識(shí)別與回憶（A1）、計(jì)算與操作（A2）和解釋與交流（A3），應(yīng)用實(shí)踐（B）包含分析與概括（B1）、推理與論證（B2）和簡單問題解決（B3），遷移創(chuàng)新（O）包含綜合應(yīng)用（O1）、猜想與發(fā)現(xiàn)（O2）和探究與建模（O3）。

根據(jù)能力框架，對本研究中教師的提問編碼，主要選取教師在課堂中的有效提問，即更關(guān)注復(fù)雜性問題的提問，刪除了一些無效的提問，如口頭禪式的“對嗎”等無意義提問，將教師的有效提問以文本形式記錄下來，并對問題背景進(jìn)行補(bǔ)充，將問題基于模型進(jìn)行編碼。編碼示例如表1所示。

表1 數(shù)學(xué)學(xué)科3×3能力要素課堂提問示例

探究與建模（O3）是指能用所學(xué)新知識(shí)探究解決新問題的方法或能從現(xiàn)實(shí)情境中抽象出數(shù)學(xué)問題，借助數(shù)學(xué)語言、符號(hào)、定理等構(gòu)建模型并據(jù)此解決實(shí)際問題。研究的課例中未出現(xiàn)該層次問題，以下是一種范例。在示例的猜想與發(fā)現(xiàn)（O2）層級(jí)問題的基礎(chǔ)上，若將提問內(nèi)容改為：點(diǎn)A，B兩個(gè)小區(qū)，準(zhǔn)備在附近建立一個(gè)菜鳥驛站P，請思考點(diǎn)P的位置并給出解釋或證明，則達(dá)到探究與建模（O3）層次。

二、教師在教學(xué)各個(gè)環(huán)節(jié)中提問的狀況分析

結(jié)合編碼結(jié)果，從能力要素和能力水平兩個(gè)維度，以總體描述、第一課時(shí)和第二、三課時(shí)（連堂）的環(huán)節(jié)描述能力水平變化趨勢這兩個(gè)部分進(jìn)行分析。

（一）教師提問的總體水平

課堂提問結(jié)構(gòu)如圖1所示，共涉及66個(gè)分析單元，8種能力水平。從能力要素來看，60.6%的提問屬于學(xué)習(xí)理解要素，33.3%的提問屬于應(yīng)用實(shí)踐要素，6.1%的問題屬于遷移創(chuàng)新要素。從能力水平來看，比例最高的為A3水平，其次是B1水平，這兩種能力水平的提問在課堂中占比達(dá)57%，未涉及對學(xué)科能力要求最高的O3水平的問題。

圖1 課堂提問結(jié)構(gòu)

總的來看，該教師的課堂問題以學(xué)習(xí)理解和應(yīng)用實(shí)踐為主；從能力水平層面來看，以解釋與交流（A3）和分析與概括（B1）水平層級(jí)為主，而要求較高的需要建立模型（O3）的問題基本不涉及。

（二）教師課堂環(huán)節(jié)提問的分布

第一節(jié)課的各環(huán)節(jié)不同水平問題數(shù)量及分布分別如圖2所示，四個(gè)環(huán)節(jié)中，僅前兩個(gè)環(huán)節(jié)里出現(xiàn)了A1水平的問題；而A2水平的問題僅在后兩個(gè)環(huán)節(jié)出現(xiàn)；另外，B2水平問題只在導(dǎo)入新課環(huán)節(jié)出現(xiàn)，A3水平的問題幾乎貫穿課堂全過程。

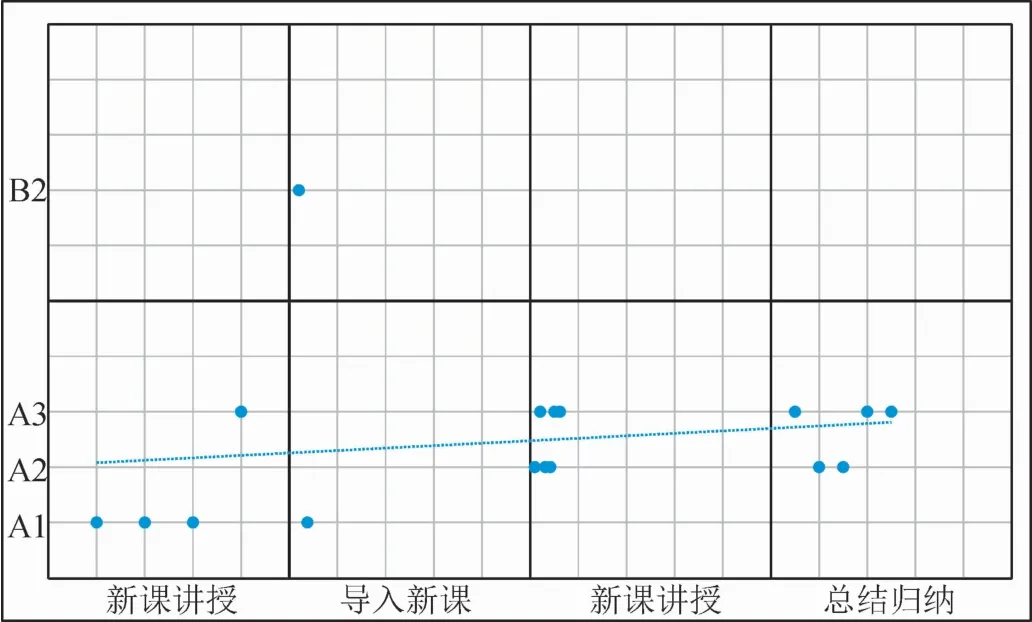
圖2 第一節(jié)課問題能力水平發(fā)展趨勢

第二、三課時(shí)提問的問題水平分布如圖3所示，本節(jié)課沒有復(fù)習(xí)提問環(huán)節(jié)；A3水平的問題幾乎貫穿整節(jié)課；在新課講授環(huán)節(jié)出現(xiàn)的問題水平層次最豐富，出現(xiàn)頻率最高的是A3和B1水平的問題。

圖3 第二、三節(jié)連堂課問題能力水平發(fā)展趨勢

觀察兩節(jié)課各環(huán)節(jié)的問題分布，可見隨著課堂環(huán)節(jié)的推進(jìn)，問題的能力層級(jí)逐漸上升、問題種類逐漸豐富。

（三）教師提問的課堂片段分析

C能力要素的問題對學(xué)生能力要求較高，在課堂中占比較少。Z老師在拋出這類問題時(shí)，會(huì)形成能力水平趨勢下降的問題鏈，以下面的教學(xué)片段為例。

該片段選自Z老師連堂課，教師和學(xué)生已完成線段垂直平分線性質(zhì)的推演歸納。教師通過性質(zhì)的語句結(jié)構(gòu)啟發(fā)學(xué)生聯(lián)想起角平分線的性質(zhì)，過渡到將兩條性質(zhì)進(jìn)行對比。該片段7個(gè)分析單元的能力水平如圖4所示，涉及A、B、C三種能力要素，能力水平變化的趨勢是下降的。

圖4 教學(xué)片段問題能力水平變化

（標(biāo)注“……”處教師語速放慢，有停頓）

教師：有學(xué)生說到角平分線。角平分線的第二條性質(zhì)是什么？（A1）

學(xué)生：到角兩邊距離相等的點(diǎn)在角的平分線上。

教師：為什么它們在表達(dá)上有高度的一致呢？（C1）首先我們把這兩條性質(zhì)再熟悉一下，然后請你們思考這個(gè)問題。

學(xué)生A：這兩條線都平分了圖形，中垂線是線段的對稱軸，角平分線平分角。

教師：你說說它們到底是怎么一致的呢？（A3）

學(xué)生：中垂線上的點(diǎn)和線段兩端點(diǎn)的連線形成了一個(gè)角，中垂線同時(shí)也是它的角平分線。

教師讓學(xué)生思考角平分線和中垂線的性質(zhì)為什么在表達(dá)上有高度的一致性，提問從簡單回憶（A1），到深入思考兩條性質(zhì)的觀察和比較（C1），對學(xué)生的學(xué)科能力、思維深度要求較高。學(xué)生發(fā)現(xiàn)了兩條線的共性：軸對稱性，并且找到了聯(lián)系兩條線的一種視角——由線段垂直平分線“找到”角平分線的過程。教師追問考查了學(xué)生運(yùn)用數(shù)學(xué)語言解釋、表達(dá)的能力（A3）。

教師：很好。事實(shí)上，如果你把線段的中點(diǎn)看成是角的頂點(diǎn)，這就是一個(gè)平角，中垂線是它的角平分線。這就是兩者的聯(lián)系。如果頂點(diǎn)動(dòng)起來，角的兩邊也會(huì)動(dòng)起來，大家會(huì)更形象地看到角平分線是怎么變化的。這樣我們從中垂線里“看到”了角平分線。那大家能從角平分線里“看到”中垂線嗎？（B2）

學(xué)生：把角“掰開”。

教師：對，我們可以把角掰成平角，一條邊不動(dòng)，另一條邊旋轉(zhuǎn)。他剛剛提到很關(guān)鍵的一點(diǎn)，中垂線和角平分線都平分圖形。我們旋轉(zhuǎn)這個(gè)角的一條邊時(shí)，角平分線會(huì)跟著動(dòng)。我們再回到軸對稱性，線段的對稱軸是……（A3）

學(xué)生：線段的垂直平分線。

教師：而角的對稱軸是……（A3）

教師＆學(xué)生：角平分線所在直線。

教師：一個(gè)說的是垂直平分線，一個(gè)強(qiáng)調(diào)了所在直線，原因是……（A3）

學(xué)生：角平分線是射線。

教師：沒錯(cuò)，對稱軸是一條直線，角平分線是射線，所以要強(qiáng)調(diào)“所在直線”，我們要注意話要說得嚴(yán)密。剛才這個(gè)問題歸根結(jié)底，線段和角都是軸對稱圖形，而我們研究的對象（線段垂直平分線和角平分線）恰好是它們的對稱軸。這種相似就帶來了我們在性質(zhì)研究時(shí)的相似。

教師順著學(xué)生的思路講解了角的頂點(diǎn)為線段中點(diǎn)的特例，其作為學(xué)生推導(dǎo)兩條性質(zhì)關(guān)系的一個(gè)案例，同時(shí)為學(xué)生逆向思考埋下伏筆。教師讓靜態(tài)的問題變得動(dòng)態(tài)化，并順理成章地拋出了反過來思考二者關(guān)系的問題，有了前面的特例，學(xué)生更容易想到把角“掰成”平角。

該片段中，教師先用A1問題引發(fā)學(xué)生思考，在提出核心的C1問題后，通過以A3水平為主的提問、追問，形成了一個(gè)問題鏈，啟發(fā)學(xué)生將舊知與新知建立聯(lián)系，并且借助B2水平提問用正推、逆推兩種思路闡釋自己的看法。

三、結(jié)論與討論

（一）教師傾向于使用解釋和分析水平的提問

教師課堂的提問水平以解釋和分析水平為主，對應(yīng)編碼為A3和B1，在能力框架中處于較低的水平。產(chǎn)生該現(xiàn)象的原因有兩方面，首先由于所選三堂連續(xù)課為新授課，學(xué)生首次接觸新知識(shí)，水平較低的問題能幫助學(xué)生理解新知識(shí)，并培養(yǎng)數(shù)學(xué)表征和數(shù)學(xué)交流的能力；其次，新版初中數(shù)學(xué)課程標(biāo)準(zhǔn)更加關(guān)注學(xué)科核心素養(yǎng)中學(xué)科關(guān)鍵能力的形成。因此在課堂中，教師將重點(diǎn)放在通過提問影響學(xué)生的知識(shí)理解，進(jìn)而培養(yǎng)學(xué)生學(xué)科關(guān)鍵能力上。專家型教師善于使用讓學(xué)生解釋自己思路的提問，并結(jié)合所學(xué)新知識(shí)進(jìn)行思考、歸納與總結(jié)，這能促進(jìn)學(xué)生對知識(shí)的深入理解，因此教師傾向于選擇解釋與交流（A3）和分析與概括能力水平的提問。

（二）教師課堂提問水平呈現(xiàn)螺旋上升的趨勢

教師在課堂提問中，不宜長時(shí)間停留在“已知區(qū)”與“未知區(qū)”，而應(yīng)在學(xué)生的知識(shí)“增長點(diǎn)”上設(shè)置懸念。第一節(jié)課的課堂提問的學(xué)科能力水平較為均衡。連堂課的新課講授環(huán)節(jié)個(gè)別問題展現(xiàn)出了更高的層級(jí)，一定程度上提升了課堂提問的學(xué)科能力水平。“對稱軸性質(zhì)的深度探討”是本節(jié)課的教學(xué)重點(diǎn)，在這節(jié)課中，學(xué)科能力層級(jí)經(jīng)歷了從學(xué)習(xí)理解（A）到遷移創(chuàng)新（C）的過程，并呈現(xiàn)出循環(huán)往復(fù)、不斷轉(zhuǎn)化、螺旋上升的特點(diǎn)。從教師提問的反饋中，能發(fā)現(xiàn)學(xué)生在該教學(xué)環(huán)節(jié)持續(xù)形成了不同水平的學(xué)科能力，且接受層級(jí)不斷提高。

（三）教師對問題進(jìn)行拆解，便于學(xué)生探究

C能力要素水平對學(xué)生的學(xué)科能力要求較高，Z老師作為專家型教師在處理該能力層次的問題時(shí)，利用問題鏈將其進(jìn)行拆分。問題鏈的設(shè)置指向?qū)W科核心問題，具有層次性、遞變性，教師從學(xué)習(xí)理解型問題入手，引導(dǎo)學(xué)生回顧與本節(jié)課新知相關(guān)的舊知，為后續(xù)知識(shí)的運(yùn)用及對比埋下伏筆，然后提升問題的水平，把學(xué)生引向問題的關(guān)鍵處，為學(xué)生的思考建立支架，幫助學(xué)生在綜合運(yùn)用知識(shí)解決問題的過程中實(shí)現(xiàn)遷移創(chuàng)新，培養(yǎng)學(xué)生的學(xué)科能力。