GA-ALNS算法的帶可容忍時間窗的VRP求解

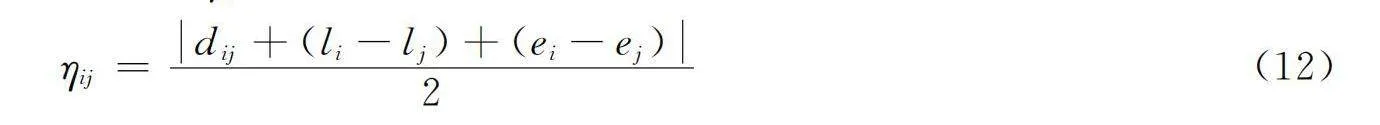
摘 要：針對帶可容忍時間窗的車輛路徑規劃問題建立最小化配送總成本的規劃模型，結合遺傳算法構造改進自適應大鄰域搜索算法對該問題求解。利用遺傳算法構建高質量解開始自適應大鄰域搜索尋優，減小算法計算時間成本；加入3種破壞算子和3種修復算子，以增加種群多樣性；嵌入模擬退火接受準則以一定概率接受較差解，自適應更新破壞和修復算子權重，避免算法陷入局部最優。選取Solomon標準測試集進行3組實驗，與已知最優解比較距離成本驗證算法可行性；在單邊容忍度時間窗模型下，與基礎ALNS算法對比驗證算法改進效果；在雙邊可容忍時間窗模型下，與相關文獻的最優結果對比。實驗結果表明，提出的GA-ALNS算法改進效果較為顯著，求得的最優解同其他算法相比優化率較好，計算得到的最優方案能實現更低的車輛配送總成本，具有一定的可行性和有效性。

關 鍵 詞：氧化鈷; 納米結構; 電容器; 電催化可容忍時間窗； 車輛路徑規劃問題； 自適應大鄰域搜索算法； 遺傳算法； 模擬退火接受準則

中圖分類號：TP18；U116.2 文獻標志碼：A

doi：10.3969/j.issn.1673-5862.2024.03.014

GA-ALNS algorithm for solving VRP with tolerable time window

CUI Song^1，2， LYU Yan^1，2， CHEN Lanfeng^1，2BAI Xueyuan， ZHANG Lei， LI Lin

（1. College of Physical Science and Technology， Shenyang Normal University， Shenyang 110034， China）（College of Science， Shenyang Aerospace University， Shenyang 110136， China ）

Abstract：To solve the vehicle routing problem with tolerable time window， establish a planning model minimizing the total cost， an improved adaptive large neighborhood search algorithm （GA-ALNS） is constructed with genetic algorithm to solve the problem. Use genetic algorithm to build high-quality solutions to start adaptive large neighborhood search optimization， reduce the time cost of calculation algorithm; add three destroy operators and three repair operators to increase the population diversity; embed the simulated annealing acceptance criterion to accept poor solutions with a certain probability， adaptive update destroy and repair operator weight， to avoid the algorithm falling into local optimum. The Solomon standard test set is selected for three experiments，and the distance cost is compared with the best known solution to verify the feasibility of the algorithm; compare with the basic ALNS algorithm and contrast with the optimal results of the relevant literature under the bilateral tolerance time window model. The experimental results show that the improvement effect of GA-ALNS is significant， and the optimal solution is better than other algorithms. The calculated optimal solution can achieve lower than the total cost of vehicle distribution， which has certain feasibility and effectiveness.

Key words：tolerable time window; vehicle routing problem; adaptive large neighborhood search algorithm; genetic algorithm; simulated annealing acceptance criterion

物流配送車輛的路徑規劃是電子商務的關鍵環節，為降低配送成本并增加商業盈利，需要進行適當的路徑規劃。該問題是帶時間窗的車輛路徑規劃問題（vehicle routing problem with time window，VRPTW）的實際應用，因現實中交通、天氣等不確定因素，軟時間窗相對于傳統硬時間窗更貼近實際配送情況。Solomon^［1］最先提出VRPTW，旨在滿足客戶需求的同時對配送路徑進行優化，以實現成本最小化。軟時間窗允許車輛可以不在客戶原本規定的時間窗內到達，但遲到或早到時會受到相應懲罰。

問題規模小、結構簡單的VRPTW可用精確算法求解。He等^［2］將客戶的不便成本設計成客戶服務開始時間的凸函數節點成本，用分支定界法求解。VRPTW是NP-Hard問題，計算量隨數據規模增大呈指數增長，現多用啟發式與元啟發式算法求解。Saksuriya和Likasiri^［3］將粒子群算法與局部搜索、破壞和修復算子進行結合，解決了帶客戶和服務商約束間的通用兼容匹配性的VRPTW。Shen等^［4］將蟻群算法和頭腦風暴優化算法結合，引入路徑間和路徑內交換，求解了最小化總距離的路徑規劃問題。

為求解VRPTW，Yassen等^［5］在和聲搜索算法中加入模擬退火算法（simulated annealing，SA），克服了和聲搜索收斂緩慢的問題。Marinakis等^［6］提出多適應粒子群算法，利用自適應貪婪算法產生初始解，自適應鄰域拓撲解決了粒子移動過程中的適應性。韓亞娟等^［7］考慮客戶對服務時間的偏離有一定容忍度，制定折線軟時間窗模型，這個模型在客戶規定時間內無懲罰成本，在可容忍限度內有較少懲罰成本，在限度外，需付出較多的懲罰成本。劉爍佳和李學強^［8］根據時間窗參數調整客戶優先級，利用改進的節約算法和改進的插入法分別對VRPTW求解，結果表明改進的插入法能得到更好解。

Ropke和Pisinger^［9］提出自適應大鄰域搜索（adaptive large neighborhood search，ALNS）算法，搜索過程中采用多種破壞和修復算子，每輪迭代只選擇一種，算子被選擇的概率與其歷史表現相關，且隨迭代更新。Krebs等^［10］研究帶三維加載約束的VRPTW，用混合自適應大鄰域搜索算法結合內部最深左下角填充解決集裝箱裝載問題，提出3種填充算法新變體，結果表明自由空間的填充算法更佳。Gu等^［11］利用ALNS算法解決商品受限的分批配送問題，加入了3種局部搜索算子。Li等^［12］研究同時取送貨的VRPTW，提出混合整數線性規劃模型，用ALNS算法解決大規模問題實例。Liang等^［13］研究有時間窗口和裝載調度的車輛路線問題，在ALNS算法中嵌入高效的可行性檢查機制，確定碼頭的裝載計劃和車輛訪問順序，以最小化總行駛距離。Chen等^［14］將自動駕駛機器人配送加入送貨路線中，利用ALNS算法研究VRPTWDR，為自動駕駛機器人替代最后一公里配送提供了解決方案。

基于上述研究，本文構造了改進的自適大鄰域搜索（GA-ALNS）算法求解帶可容忍時間窗的路徑規劃問題，利用遺傳算法（genetic algorithm，GA）構建質量較高的初始解，以減少算法計算時間成本；利用GA構建的初始解開始ALNS算法的尋優，加入3種破壞算子和3種修復算子增加種群多樣性，為種群生成新解；嵌入SA接受準則更新算子權重，以一定概率接受較差解，避免算法陷入局部最優。

1 問題描述及模型

1.1 問題描述

本文研究VRPTW，車輛從倉庫出發，并在規定時間內返回，對每個客戶進行不重復服務，規劃車輛的路徑讓車輛在滿足所有客戶需求的同時，盡可能降低總成本。帶可容忍度的VRPTW定義在圖G（N，E）上，節點集為N={0，1，2，…，n}，節點0表示倉庫，節點{1，2，…，n}表示需服務的客戶點，節點i∈N/{0}的需求為q_i，從節點i到j的運輸成本為C_ij，K為倉庫中心所擁有的車輛集合，Q為車輛最大載重。t_i表示到達客戶i的時間，w_i表示在客戶i的等待時間，t_ij表示客戶i到客戶j的時間，e_i表示客戶i可以服務的最早時間，l_i表示客戶i可以服務的最晚時間，s_i表示在客戶i服務的時間，β是單位車輛固定使用成本，γ是車輛單位距離的運輸成本。

1.2 帶可容忍的時間窗及懲罰函數設置

對于最佳服務時間窗的偏離，客戶有可容忍和不可容忍的區分。在傳統軟時間窗的基礎上考慮客戶容忍水平為α，提出帶可容忍的時間窗。客戶期待時間窗（e_i，l_i）加入容忍水平α后時間窗為（_i，_i），其中_i=e_i－α_is_i，_i=l_i+α_is_i，i=1，2，…，N。與傳統軟時間窗不同，該時間窗可以在滿足客戶需求的同時更好地合理配置優化資源。帶可容忍時間窗下的懲罰函數成本為

其中，p₁，p₂，p₃，p₄為懲罰函數系數，應該滿足p₁gt;p₂，p₃gt;p₂，p₃lt;p₄，p₁lt;p₄。

1.3 數學模型建立

VRPTW的數學模型可描述如下：

MinZ=γ∑k∈K∑i∈N∑j∈NC_ijx^k_ij+β∑k∈K∑j∈Nx_0jk+∑k∈K∑i∈NP（T^k_i）（2）

約束：

∑k∈K∑i∈Nx^k_ij=1j∈{1，2，…，n}，i≠j（3）

∑k∈K∑j∈Nx^k_ij=1i∈{1，2，…，n}，i≠j（4）

∑i∈N∑j∈Nx^k_ijq_i≤Qk∈K（5）

∑j∈Nx^k_ij=∑j∈Nx^k_jii=0，k∈K（6）

t₀=w₀=s₀=0（7）

∑Kk=1∑ni=0，i≠jx^k_ij（t_i+t_ij+s_i+w_i）=t_j j∈（1，2，…，n）（8）

e_i≤（t_i+w_i）≤l_i i∈（1，2，…，n）（9）

x^k_ij=1車輛k從節點i到節點j（i≠j）

0其他（10）

目標函數式（2）為服務完所有客戶點后包括車輛固定使用成本、車輛行駛總成本和懲罰成本在內的最小車輛總運輸成本，式（3）和式（4）保證每個節點僅被訪問一次，式（5）保證運輸過程中車輛載重不得超過最大載重，式（6）保證車輛從倉庫中心出發并回到倉庫中心，式（7）～（9）是時間窗約束。

2 問題求解

本文構建GA-ALNS算法，先用GA高效構建初始解，把GA搜尋的最優解作為ALNS算法初始解；繼而用3種破壞算子移除客戶點，用3種修復算子將移除客戶重新插回路徑，生成新解，破壞和修復算子可以擴大搜索解的空間，改進當前解，增大尋找到最優解的可能性；最后，根據SA接受準則判斷是否接受新解，按一定概率接受差解，避免陷入局部最優。在迭代過程中，自適應更新算子得分權重，利用輪盤賭選擇算子選擇本輪迭代所使用的算子，更多使用歷史表現優良算子，找到更優的解決方案。

2.1 遺傳算法構造初始解

基礎ALNS算法的初始解是隨機生成的，為減少迭代次數，避免算法時間成本過大，本文使用GA進行初始解構建，增大找到更好解的概率，降低算法耗時成本。利用GA生成初始解的步驟如下：

1）車輛從倉庫出發隨機選擇客戶服務，并將該客戶點從待服務列表USL中刪除，以免重復服務; 2）將選中客戶加入該路徑; 3）判斷服務該客戶后的車輛是否超載，若未超載則重復1）和2），否則車輛返回倉庫，并派出下一輛車繼續服務; 4）重復操作，直至數據集內所有客戶點都被服務完。

上述步驟每進行一次得到一個可行解，多次重復后得到初始種群，計算種群中每個解的目標函數值，利用錦標賽選擇算子選擇優良個體進行交叉變異操作。在錦標賽選擇中，從種群中隨機有放回地抽取任意TOS個個體，選最優個體進入下一代，當該個體的適應度優于其他TOS-1個“競爭者”時才能贏得錦標賽。在該過程中最差的個體永遠不會幸存，而最優個體總是能獲勝。

對優良個體進行部分匹配交叉（partially mapped crossover，PMX）操作，可挖掘種群多樣性，克服啟發式算法易陷入局部最優解的問題。根據給定交叉率（probability of crossover，PC）在優良個體中選取父代染色體進行PMX操作，交叉后得到2個子代，計算2個子代對應的目標函數值，若出現目標函數更小的解則更新父代，否則不更新。二元變異可以維持種群多樣性，一定程度上克服算法易陷入局部最優的缺陷。根據給定變異率（probability of mutation，MU）在區間（0，1）內產生隨機數，當該隨機數小于MU時，利用變異算子產生新可行解加入新種群。當達到迭代次數后，選擇遺傳算法找到的最優解作為ALNS的初始解進行后續操作。

2.2 破壞算子

本文應用3種破壞算子將客戶從當前解中移除，移除客戶后將客戶存放在破壞算子列表（destroy list，DL）中，等待后續修復算子對其進行操作。下面介紹這3種破壞算子。

1）random destroy

random destroy從當前解中隨機選擇并移除f個客戶點。該破壞算子的優點是計算速度快，并通過引入隨機性幫助算法跳出局部最優。隨機移除的操作可以增加ALNS算法的隨機性，增加種群多樣性，避免算法陷入局部最優解。

2）worst destroy

worst destroy的核心思想是將當前解中位置不合適的客戶移除，通過計算客戶點從當前解移除后的節約成本判斷客戶點的合適程度，節約成本越高代表該客戶在當前解的位置越不合適。TC^a_i和TC^b_i分別代表該客戶被移除前后的當前解成本，ΔTZ越大，說明將該客戶移除后節省的成本越高。

ΔTZ=TZ^b_i－TZ^a_i（11）

計算所有客戶的ΔTZ，并從高到低進行排序，按該順序移除客戶。為了增加算子的隨機性，移除個數在（wor_d_min，wor_d_max）中均勻抽取。該算子可以將部分使成本增多的客戶移除，從而達到減少總成本的目的。

3）related destroy

related destroy根據客戶間的相關度η_ij將客戶成對進行移除，相關度計算公式如下：

η_ij=d_ij+（l_i－l_j）+（e_i－e_j）2（12）

先隨機選擇一個客戶i進行移除，接下來計算其他客戶與i的相似度并按降序排列，從相似度高的客戶開始移除操作，直至移除足量客戶。

2.3 修復算子

下面介紹的3種修復算子將DL中客戶重新插入到解中。

1）greedy repair

greedy repair將被移除客戶插入到最好路徑的最佳位置，計算客戶i插入路徑rou_r的位置loc_q的插入成本，Δ_i=ΔI（i，r，q）=d_i，q+d_q，i+1－d_i，i+1，將客戶i插入最佳位置bestloc_q。若所有剩余要插入的客戶沒有了可行的插入位置，則生成一條新的路徑，直至所有被移除客戶都重新插回路徑中，最終得到新解。

2）regret repair

regret repair按照客戶插入成本后悔值大小來決定客戶點的插入位置，直至將DL中的客戶點都重新插入新解中。后悔值是客戶點在最佳插入位置和次佳插入位置之間的成本差異，二者差異越大，后悔值越大，代表如果不在當前位置進行插入，則未來進行插入操作花費的成本會更高，從而感到后悔。后悔值reg_i的計算公式如下：

reg_i=IZ^2nd_i-IZ^1st_i（13）

計算客戶點在每個可插入位置的后悔值，選擇后悔值最高的位置進行插入，循環迭代直至所有客戶都被插入，得到新解。

3）random repair

random repair隨機將客戶從DL中插回解的某條路徑內，直至DL中的所有客戶點都重新插入到路徑中，以產生新解。

2.4 接受準則和算子權重更新

若在尋優過程中只接受優解，則算法容易陷入局部最優。為避免該情況發生，利用模擬退火算法，允許一定差解被接受，退火過程中按照Metropolis準則以一定概率接受較差解，接受概率隨著溫度下降而減少。本文制定SA接受準則：若產生新解的總成本小于最優解，則接受該解，并將最優解和當前解都更新；若新解的總成本大于最優解但小于當前解的總成本，則接受該解，并將當前解更新；若新解的總成本大于當前解總成本，則以一定概率接受新解，概率計算如下：

RE_p=e^（Z_cur－Z_new）/TEM（14）

其中：Z_cur和Z_new分別為當前解和新解的總成本；e為自然常數；TEM為當前溫度，溫度以冷卻速率ΔTEM下降，初始溫度為TEM₀，終止溫度為TEM_e。

考慮各破壞算子和修復算子探索解的能力不同，結合SA接受準則更新算子得分權重，并利用輪盤賭算法選擇破壞算子和修復算子。初始時，所有算子的得分權重相同，在迭代過程中按表1更新算子得分，以便增大能發現優解和新解的算子的得分權重。算子探索解的能力影響算子的分值，并直接決定了算子權重，通過算子權重決定迭代過程中該算子被選中的概率。在迭代過程中，GA-ALNS算法可以根據算子的性能自適應地調整算子權重，強化搜索。

3 實驗結果及分析

本文對Solomon標準算例進行了3組實驗：第1組利用18組實例，計算硬時間窗下的車輛行駛距離，同Solomon標準算例集公布的最優解進行比較，測試本文提出的GA-ALNS算法的求解效果，驗證該算法的可行性；第2組使用基礎的ALNS算法和GA-ALNS算法在單邊可容忍時間窗模型下對18組實例進行求解并對比2種算法的結果，分析GA-ALNS算法的提升效果；第3組利用GA-ALNS算法在雙邊可容忍時間窗模型下首先對9組數據求解并同何美玲等^［15］的IACO算法的結果比較，再比較IACO算法、韓亞娟等^［7］的算法和GA-ALNS算法在計算客戶數量為25對的R101實例時的計算結果。

實驗抽取三大類兩小類共6種不同類型集群中的不同數量客戶的實例，其中R1和R2型客戶隨機分布，C1和C2客戶集群分布，RC1和RC2是以上2種的混合。算例集R1，C1和RC1的車輛載重、調度范圍較小，時間窗較緊湊；算例集R2，C2和RC2的車輛載重、調度范圍較大，時間窗較寬。

本文參數設置：GA最大迭代次數為200，ALNS算法迭代10輪，每輪20次，容忍度水平α=0.5，SA接受準則中TEM₀=100，TEM_e=0.017，ΔTEM=0.75，目標函數中所用參數同文獻［14］，車輛單位距離運輸成本γ=8，單位車輛固定使用成本β=60，懲罰函數中懲罰系數p₁=1，p₂=0.5，p₃=1.5，p₄=2，算子參數ran_min=0.1，ran_max=0.4，wor_min=0.2×C，wor_max=0.4×NC。

3.1 硬時間窗下的距離比較

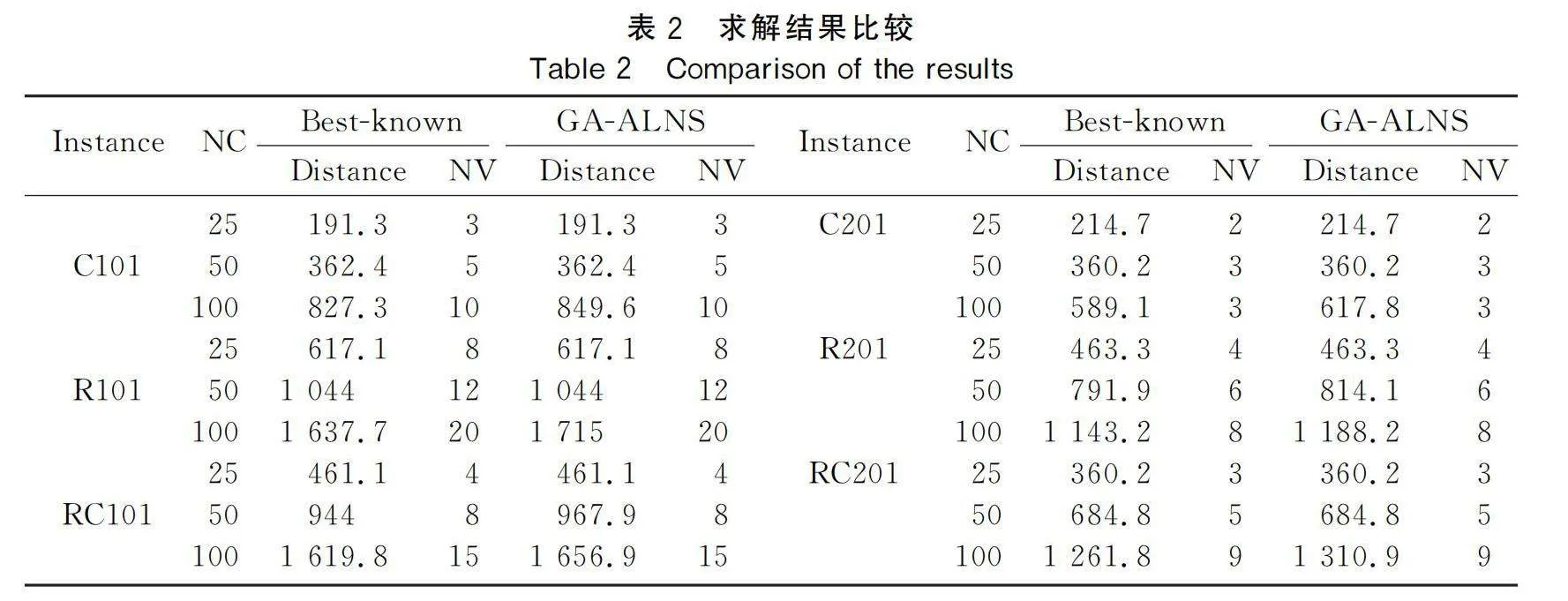
本實驗時間窗設置為硬時間窗，不允許提前或推遲服務。使用GA-ALNS算法對每個實例計算在硬時間窗下解決方案的總行駛距離，取10次計算中的最優結果同公布的最優解進行比較，其中NV代表車輛數目，NC代表客戶數量，Distance表示解決方案的總行駛距離，得到結果見表2。從表 2中可以看出：對于客戶數量為25的算例，本文算法計算出的最優解與已知最優解一致；對于客戶數量為50的算例，除R201和RC101外本文算法都達到已知最優解；對于客戶數量為100的算例，本文算法求得的解與已知最優解相比總距離稍長，但結果相差較小，誤差范圍在5%以內，所需車輛數相同，說明利用本文GA-ALNS算法求解帶可容忍時間窗車輛路徑規劃問題的可行性。

3.2 單邊可容忍時間窗模型下的實驗結果

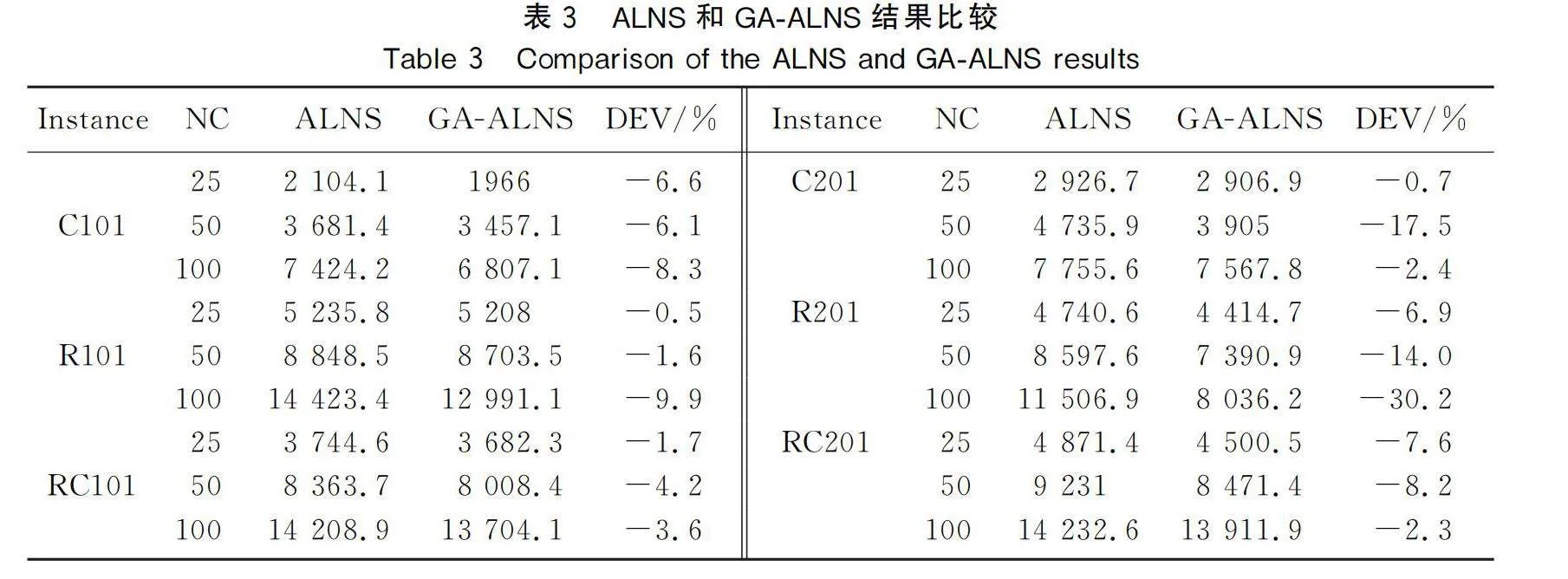
將時間窗設為單邊可容忍時間窗，即只允許提前服務客戶，且有相應懲罰成本，計算包含車輛固定使用成本、車輛行駛成本和懲罰成本的總成本。用基礎ALNS算法和GA-ALNS算法分別對18組數據運行10次，選成本最小的結果（表3），其中優化程度（develop，DEV）表示2種算法結果相比成本的優化率。

由表3可以看出，優化效果最好的R101-100實例優化率達到30.2%，效果最差的C201-25實例優化率也達到0.7%，說明不論客戶數量多少，GA-ALNS算法的結果都優于ALNS算法，改進效果顯著。

3.3 雙邊可容忍時間窗模型下的實驗結果

本實驗中，時間窗為雙邊可容忍時間窗，允許提前或延后服務客戶，若不在規定時間窗服務，則按照懲罰函數的設置付出相應的懲罰成本，進而計算包含車輛固定使用成本、車輛行駛成本和懲罰成本的總成本。本文的GA-ALNS算法對9組數據分別運行10次，選成本最小的結果與何美玲等^［15］的IACO算法公布的最優解進行比較（表4），其中NC表示客戶數量，DEV表示二者相比GA-ALNS計算結果的優化率。

表 4表明二者最優解的比較結果優化率都是負數，且優化效果較為顯著，優化效果最多的C201-50實例優化率達到了38.6%，除優化率為1.7%的RC201-100實例外，其他實例的優化率都在10%～37%，說明不論客戶數量大小，GA-ALNS算法的計算結果都優于IACO算法。

表5為IACO^［15］算法、韓亞娟等^［7］的算法和GA-ALNS算法分別對客戶數量為25的R101實例計算的最優結果比較。其中無懲罰成本包括車輛固定使用成本和車輛行駛距離成本，NV表示車輛數目。結果表明，雖然IACO算法最優解的無懲罰成本最低，但GA-ALNS算法的最優解總成本最低，說明該算法在解決帶可容忍時間窗的VRP時有一定優勢。

4 結 語

本文針對帶可容忍時間窗的車輛路徑規劃問題構建了GA-ALNS算法，利用遺傳算法高效構建了ALNS算法的初始解，降低了計算時間成本；結合3種破壞算子移除路線中的客戶點，利用3種修復算子將客戶重新插入回路徑，生成新的解決方案，擴大了解空間，增大了搜尋最優解的可能性。嵌入模擬退火接受準則按一定概率接受差解，避免算法陷入局部最優，在迭代過程中，自適應更新算子得分權重，更多地使用歷史表現優良的算子，最終找到了最佳的路徑規劃方案。

利用Solomon測試集驗證算法的改進效果和可行性、有效性，實驗結果表明：本文算法在硬時間窗下能得到與已知最優解相同或十分接近的解；在單邊容忍時間窗模型下，不論客戶數量多少，同基礎ALNS算法相比，GA-ALNS算法都能得到更好解，顯著降低了配送總成本，改進效果顯著；在雙邊容忍時間窗模型下，與IACO算法^［15］最優解進行比較，9組數據運行結果都能得到總成本更小的解；IACO^［15］算法、韓亞娟等^［7］的算法和GA-ALNS算法分別對客戶數量為25的R101實例計算，GA-ALNS算法也得到花費總成本最低的解決方案，這表明該算法在解決帶容忍度時間窗的車輛路徑規劃問題時有一定優勢。

參考文獻：

［1］KRAJCINOVIC D，FONSEKA G U.The continuous damage theory of brittle materials［J］.J Appl Mech，1981，48（4）：809-824.

SOLOMON M M.Algorithms for the vehicle routing and scheduling problems with time window constraints［J］.Oper Res，1987，35（2）：254-265.

［2］HE Q，IRNICH S，SONG Y J.Branch-Cut-and-Price for the vehicle routing problem with time windows and convex node costs［J］.Transport Sci，2019，53（5）：1409-1426.

［3］SAKSURIYA P，LIKASIRI C.Hybrid Heuristic for vehicle routing problem with time windows and compatibility constraints in home healthcare system［J］.Appl Sci，2022，12（13）：6486.

［4］SHEN Y，LIU M D，YANG J，et al.A hybrid swarm intelligence algorithm for vehicle routing problem with time windows［J］.IEEE Access，2020，8：93882-93893.

［5］YASSEN E T，AYOB M，NAZRI M Z A，et al.A hybrid meta-Heuristic algorithm for vehicle routing problem with time windows［J］.Int J Artif Intell Tools，2015，24（6）：1550021.

［6］MARINAKIS Y，MARINAKI M，MIGDALAS A.A multi-adaptive particle swarm optimization for the vehicle routing problem with time windows［J］.Inf Sci，2019，481：311-329.

［7］韓亞娟，彭運芳，魏航，等.超啟發式遺傳算法求解帶軟時間窗的車輛路徑問題［J］，計算機集成制造系統，2019，25（10）：2571-2579.

［8］劉爍佳，李學強.基于啟發式帶時間窗的車輛路徑規劃問題求解［J］.計算機系統應用，2022，31（11）：275-281.

［9］ROPKE S，PISINGER D.An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows［J］.Transport Sci，2006，40（4）：455-472.

［10］KREBS C，EHMKE J F，Koch H.Effective loading in combined vehicle routing and container loading problems［J］.Comput Oper Res，2023，149：105988.

［11］GU W J，CATTARUZZA D，OGIER M，et al.Adaptive large neighborhood search for the commodity constrained split delivery VRP［J］.Comput Oper Res，2019，112：104761.

［12］LI W L，LI K P，RAM KUMAR P N，et al.Simultaneous product and service delivery vehicle routing problem with time windows and order release dates［J］.Appl Math Model，2021，89：669-687.

［13］LIANG Y J，WANG X，LUO Z X，et al.Integrated optimisation of loading schedules and delivery routes［J］.Int J Prod Res，2022，61（2）：1-18.

［14］CHEN C，DEMIR E，HUANG Y.An adaptive large neighborhood search heuristic for the vehicle routing problem with time windows and delivery robots［J］.Eur J Oper Res，2021，294（3）：1164-1180.

［15］何美玲，魏志秀，武曉暉，等.基于改進的蟻群算法求解帶軟時間窗的車輛路徑問題［J］.計算機集成制造系統，2023，29（3）：1029-1039.

【責任編輯：溫學兵】