基于“認知結構”發展的數學教學分析
楊晶晶

摘要:以“數列通項公式”的解題教學為載體,以認知結構的理論作為研究依據,從組建解題模塊,提升解題能力的角度展開分析與研究,提出數列相關問題存在無遞推公式與有遞推公式兩類情況.文章從這兩類情況著手,探尋數列通項公式解題模塊的實際應用情況,幫助學生建構一類解題結構,以提高解題能力.
關鍵詞:解題模塊;認知結構;通項公式
認知心理學研究發現:學習過程實則為不斷構建與完善認知結構的過程,認知結構對數學教學有著至關重要的影響.奧蘇貝爾提出:認知結構是指學生頭腦中的知識結構,從廣義的角度來看,它指一種觀念的全部內容;從狹義的角度來看,認知結構是學習者在某一特定領域的觀念或組織.解題模塊屬于重要的認知結構,對學生的解題能力發展具有直接影響.
1 組建解題模塊
教學中,常會遇到這樣一種現象:教師反復強調并講了幾遍的內容,學生卻屢屢出錯;還有一些學生課堂上能夠對答如流,課后作業卻漏洞百出.出現這些現象的主要原因就在于學生并沒有將新知納入到自己的認知結構中,還沒有形成良好的解題模塊.研究發現,解題模塊能將某些雜亂無章的解題過程變得有法可依、有據可循,降低解題的難度.
要求解數列問題,首先就要對這部分知識結構有一個明確的認識.應將教材中與數列通項公式相關的知識羅列到一起,再分門別類地進行歸納,這樣在解題時就能夠從中探尋出相應的方法.
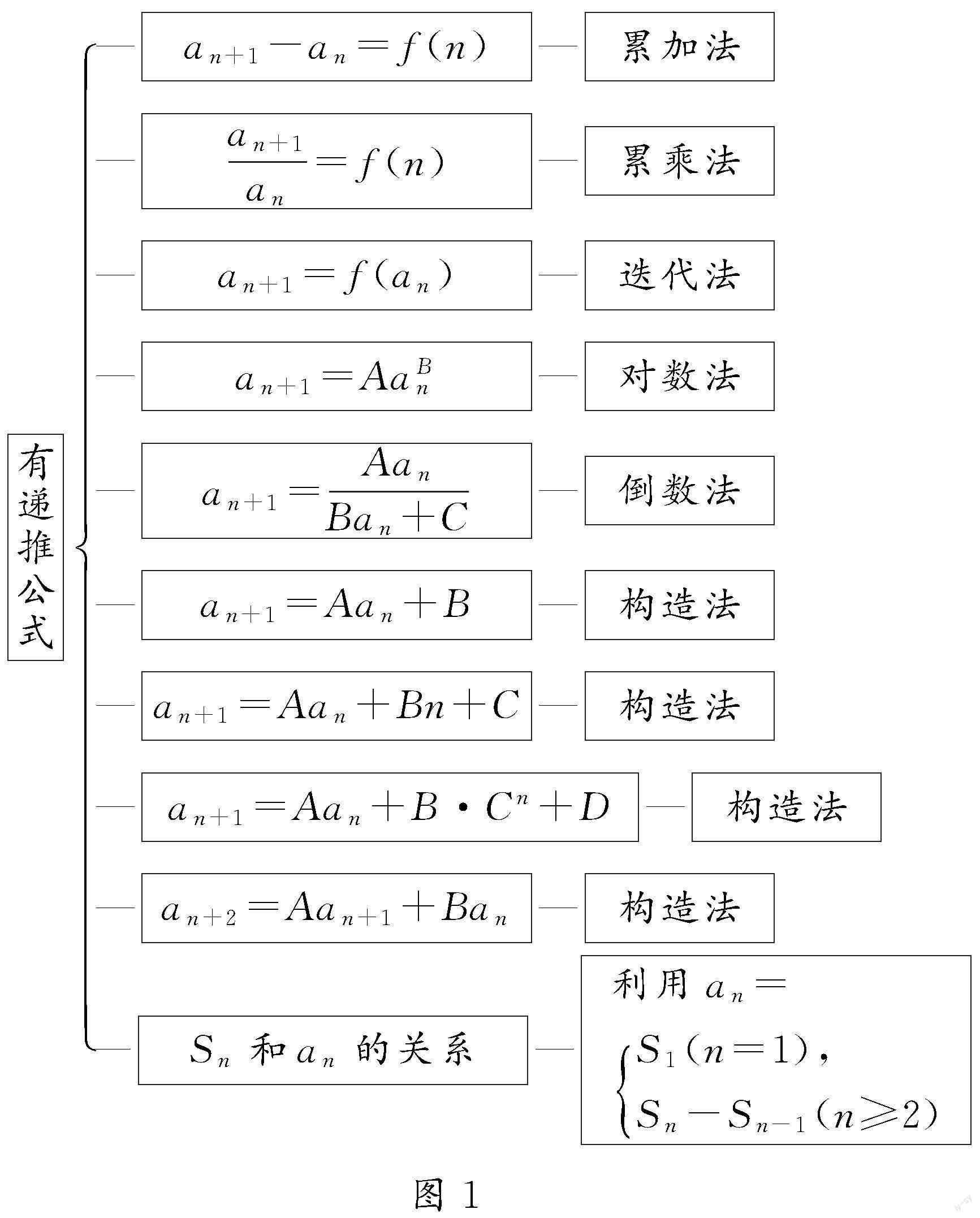
數列通項公式的相關問題,若題干條件中不存在遞推公式,可將它分為“通過列舉數字、圖形與圖象表示”“已知數列的某幾項的值”“已知某個數列的前幾項和與值”三類;若題干條件中存在遞推公式,可分為多類情況(見圖1).
一般情況下,解決無遞推公式的數列問題,可應用公式法與觀察法,這類問題的難度系數偏小,比較容易獲得結論;而有遞推公式的數列問題類型多樣且靈活,高中階段常接觸到的有圖1中的十類情況,且每一類情況都存在相對應的解法.這就組成了解數列通項公式的解題模塊,模塊的形成為解決相應的問題提供了幫助.
2 應用解題模塊
張景中院士對于解數學問題提出了如下看法:無招勝有招是練武的最高境界,但練武依然需要從一招一式開始,解數學問題亦如此,都要通過一點一滴的訓練與建構,才能達到“無招勝有招”的境界.對于大部分學生而言,需要充分重視變式訓練,學會將數學問題分門別類,以探尋出可機械執行的巧法,也就是算法.
由此可以看出,組建解題模塊是實施快速解題的上上之策,即幫助學生在腦海中建構解決一類問題的認知結構.實施解題存在多種方法,如將題干中一些隱性的條件顯露出來,將一些雜亂無章、冗長繁雜的解答過程變得條理清晰、簡潔明了等,可從最大程度上降低解題的難度.
(1)無遞推公式類
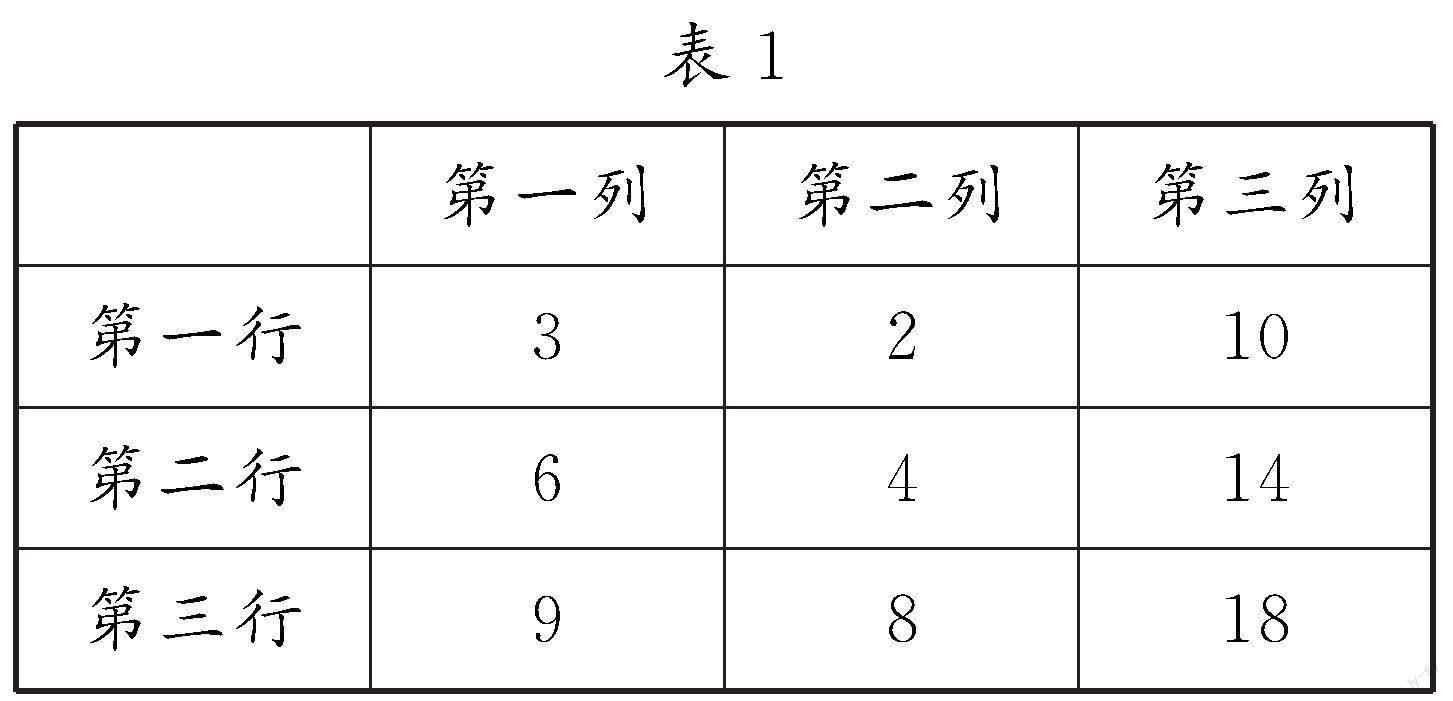
例1 已知等比數列{an}中的a1,a2,a3分別為表1第一、二、三行中的某個數,并且a1,a2,a3中的任何兩個數不處于同一列,求該數列的通項公式.
觀察發現,本題并未給出遞推公式,而且以圖表法展示題干,對應解題模塊可通過“觀察法”來探尋數字間所存在的規律.
解:當a1=3時,與題意不符;當a1=2時,有且僅有a2=6,a3=18,與題意相符;當a1=10時,與題意不符.由此可以確定a1=2,a2=6,a3=18,那么等比數列{an}的公比q=3,其通項公式為an=2·3n-1.
(2)有遞推公式,如an+1=Aan+B·Cn+D類型
例2 已知數列{an}中的a1=1,an+1=2an+3n+1,求該數列的通項公式.
分析:題干有遞推公式,且屬于an+1=Aan+B·Cn+D型,對照圖1的解題模塊,可以考慮應用構造法實施解題.具體解法如下.
解法1:設存在實數λ,使得an+1+λ·3n+1=2(an+λ·3n),即an+1=2an-λ·3n,計算得λ=-3,那么an+1-3n+2=2(an-3n+1).令bn=an-3n+1,則由a1=1可知數列{bn}為一個等比數列,其首項為-8,公比為2,因此可獲得數列{an}的通項公式為an=3n+1-2n+2.
例3 (1)定義首項為1,公比為正數的等比數列是“M-數列”.
{an}(n∈N*)為等比數列,且滿足a3-4a2+4a1=0,a2a4=a5,請證明:數列{an}為“M-數列”.
分析:第(1)問可以直接證明.第(2)問中題干的遞
3 注意事項
3.1 理解解題模塊是應用的前提
應用解題模塊實施解題,并不是所有的問題都能夠歸結到相應的類型.如一些開放題或證明題等,并沒有通用通法可以直接套用.教師不能直接帶領學生識記解題模塊,而應與學生一起探索解題模塊形成的前因后果,讓學生對解題模塊的形成過程、蘊含的數學思想方法等有一定的了解,在此基礎上再進行記憶與應用.
3.2 聯系實例記憶解題模塊
一個完整的解題模塊應包含有利于學生理解的具體實例,以便于學生記憶與應用.這里所提到的實例必須具有典型性與代表性,當學生遇到與之類似的問題時,能夠從解題模塊中的典例著手分析,實現知識的正遷移,提高解題能力.
3.3 在“通法”的基礎上補充“巧法”
解題模塊作為解題的通性通法確實能有效提高解題效率,而“通法”的應用并不排斥其他新的更巧妙的方法的應用.應用解題模塊進行解題教學的過程中,適當地補充一些更巧妙的方法,還能進一步發展學生的數學思維,完善學生的認知結構.
達爾文認為:與方法相關的知識是最有價值的知識.師生通過解題訓練總結解題經驗方法的過程中,可有針對性地完善不同題型與類別的解題模塊,以促使知識的正遷移,讓學生能更快、更準地將解題模塊應用在實際解題中.
事實證明,解題模塊的引入與應用不僅提高了學生的解題能力,還有效促進了學生反思習慣的形成.當學生面對一些錯題時,會不由自主地探尋問題所歸屬的類別,并想方設法來解決它,甚至有學生會自主創建出新的解題模塊,形成良好的認知結構.

