正交于頂，隱含定點

黃軼

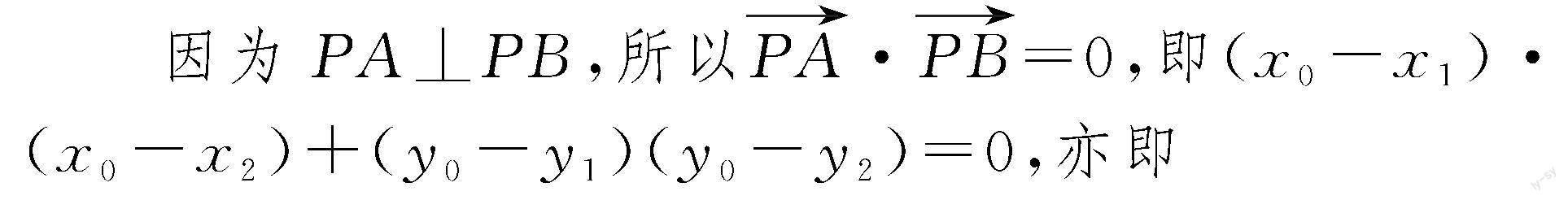
摘要：基于一道涉及拋物線的教材習題，追根溯源，通過對問題的反思，合理逆向思維，類比拓展，總結規律.結合邏輯推理與數學運算，得到拋物線中過定點兩弦相關斜率代數關系式為定值背景下的一些優美結論，拓展學生思維，提升數學能力，培養數學核心素養．

關鍵詞：拋物線；教材；類比；斜率；拓展

數學家波利亞曾說：“一個認真備課的教師能夠拿出一個有意義但又不太復雜的題目，去幫助學生發展問題的各個方面，使得通過這道題，就好像通過一道門戶，把學生引入一個完整的理論領域．”［1］特別地，教材中的一些典型的例題或習題，其背景深刻，知識豐富，典型性高，拓展性強，蘊含豐富的數學思想方法，如果有針對性地加以利用，有思想性地引導，有方向性地探究，有思維性地拓展，則可以全面提升學生的數學品質，提高數學能力，培養數學核心素養［2］．

1 源于教材

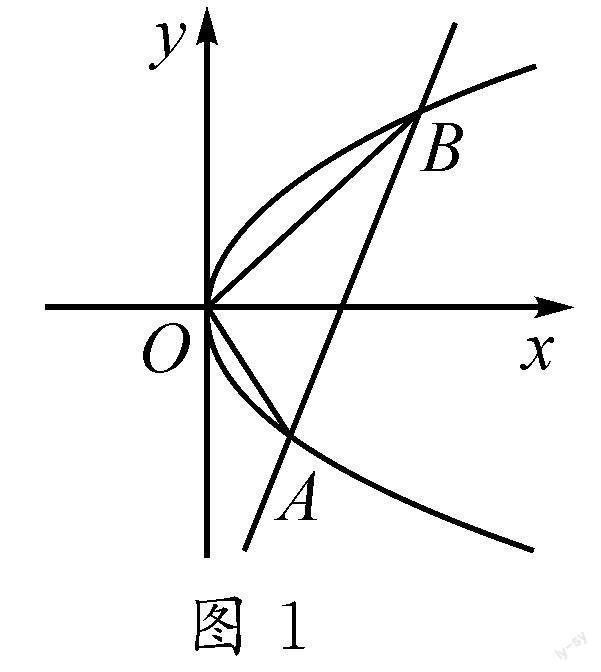
例題 〔人教版《數學》（選擇性必修第一冊）3.3拋物線第138頁第6題〕如圖1，直線y=x－2與拋物線y2=2x相交于A，B兩點，求證：OA⊥OB．

設A（x1，y1），B（x2，y2），則y1y2=－4.

故OA⊥OB．

反思：根據拋物線關于對稱軸的對稱性，將上述例題中的直線“y=x－2”替換成直線“y=2－x”（兩直線的圖象關于x軸對稱），同樣可得結論OA⊥OB．而直線y=x－2與直線y=2－x有公共點（2，0），結合拋物線y2=2x可知2p=2，那么直線y=x-2過點（2，0）與OA⊥OB之間是否存在某種特殊的聯系呢？

2類比拓展

以上問題的實質就是拋物線的弦對頂點張直角的相關性質（拋物線的弦對頂點張直角時恒過定點）．借助邏輯推理、思維拓展、類比提升等，可以對拋物線過頂點（或其他定點）的兩弦斜率之積、斜率之和、斜率倒數之和等為定值的相關結論，進一步加以歸納、推廣與總結．

2.1 拋物線過頂點兩弦斜率之積為定值

結論1 已知A，B為拋物線y2=2px（p>0）上兩動點，O為坐標原點.若OA⊥OB，則直線AB恒過定點（2p，0）．

證明：設A（x1，y1），B（x2，y2），直線AB的方程為x=my+t.

因此，對于上述教材中的習題，因為拋物線y2=2x中的p=1，并且直線y=x－2經過點（2，0），所以有OA⊥OB成立．

結論1是其推廣的特例，是當常數SymbollA@=－1時的結果．

推廣的證明可參照結論1的證明加以分析與處理，這里不多贅述．

2.2 拋物線過定點兩弦斜率之積為定值

結論2 已知A，B為拋物線y2=2px（p>0）上兩動點，P（x0，y0）為拋物線上一定點，且滿足PA⊥PB，則直線AB恒過定點（2p+x0，－y0）．

證明：設A（x1，y1），B（x2，y2）.

（y20－y21）（y20－y22）+4p2（y0－y1）（y0－y2）=0.

整理可得（y0+y1）（y0+y2）=－4p2，則有y1y2=－4p2－（y1+y2）y0－y20=－4p2－（y1+y2）y0－2px0.

由此可知，直線AB恒過定點（2p+x0，－y0）.

經檢驗，當x1=x2時，也滿足.

因此，直線AB恒過定點（2p+x0，－y0）．

2.3 拋物線過定點兩弦斜率之和為定值

證明：設A（x1，y1），B（x2，y2），直線AB的方程為x=my+t.

推廣 已知A，B為拋物線y2=2px（p>0）上兩

2.4 拋物線過定點兩弦斜率倒數之和為定值

證明：設A（x1，y1），B（x2，y2），直線AB的方程為x=my+t.

y2－2pmy－2pt=0.

由韋達定理，可得y1+y2=2pm.

3 教學啟示

上文中以一道課本習題為源，得到拋物線中過定點的兩弦斜率之積、斜率之和、斜率倒數之和為定值條件下的相應的優美結論，合理反思總結，拓展思維，總結規律，構建全面的邏輯思維體系與應用．

事實上，拋物線中的相關結論及其推廣，還可以進一步拓展到圓錐曲線中去，有關圓錐曲線斜率之積（或之和、倒數之和）為定值的問題層出不窮．當我們站在系統的高度，合理地整合知識，很多時候都能有一個思維方向，避免進入無頭緒的計算誤區，全面提升能力，養成思維習慣，培養數學核心素養．

參考文獻：

［1］江南岸.改進解題教學 提升復習效益——高三復習解題教學策略例談［J］.上海中學數學，2020（10）：4-7，17.

［2］蔣自佳.基于問題驅動的一類定點定值問題探究［J］.高中數學教與學，2022（13）：13-16.