高考數學審題五環節

江蘇省高郵市第一中學 薛晉紅

數學審題就是正確弄清題目條件與內涵,這是解題的基礎,是能否正確、迅速解題的關鍵.因而要想有效解決數學問題,關鍵就是要把好審題關.如果審題掉以輕心,往往會導致數學思維的偏差,致使解題失誤或陷入到繁冗的解題中[1].

1 環節一:題設字斟句酌,全面弄清題意

認真細致審題的重要策略就是逐字逐句地仔細分析,特別是一些容易看錯、理解錯、被忽視或被誤解的字、詞、句等,要善于“字斟句酌”,弄清題意與內涵實質,為正確數學解題創造條件.

例1(2022年高考數學上海卷·10)已知等差數列{an}的公差不為零,Sn為其前n項和,若S5=0,則Si(i=1,2,3,……,100)中不同的數值有______個.

審題：結合題設,抓住等差數列的背景,理解其中的關鍵語句“S5=0”,合理建立關系式,確定等差數列的首項與公差之間的關系,結合等差數列的前n項和將所求問題轉化為二次函數的相關問題,弄清問題的內涵與實質,并結合圖象的對稱性來分析與應用.

由d≠0,利用二次函數的圖象與性質,可知Si(i=1,2,3,……,100)中S5=0,S2=S3=-3d,S1=S4=-2d,S6=3d,S7=7d,……,其余各項均不相等.

所以Si(i=1,2,3,……,100)中不同的數值有100-2=98(個).

故填答案:98.

2 環節二:抓住問題本質,合理切入突破

解題過程中,審題時要注意題設條件中的一些關鍵性字、詞、句等,抓住問題的本質,為解題突破口與切入點的尋找提供依據,也是數學思維的關鍵點.

例2(2022年高考數學新高考Ⅰ卷·5)從2至8的7個整數中隨機取2個不同的數,則這2個數互質的概率為( ).

審題：以古典概型的形式設置問題,抓住題中的關鍵詞“2個數互質”,結合計數原理與排列組合、概率等相關知識來綜合與應用.特別,針對關鍵詞的理解與切入,當中隱藏一組特殊的數(3,6),這里容易遺漏而導致錯誤.

所取的2個數不互質的不同取法有(2,4),(2,6),(2,8),(3,6),(4,6),(4,8),(6,8),共7種.

3 環節三:善于變形轉化,實現化繁為簡

在具體解題過程中,審題時要善于對題設中給出的已知條件或所求的結論形式進行必要的變形與簡化,這是實現化繁為簡,有效尋找解題方法和途徑的一種基本策略與技巧方法.

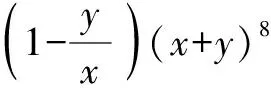
故填答案:-28.

4 環節四:尋求問題轉換,巧妙化生為熟

數學審題時,不能只停留在問題的題設條件上,要合理轉換,將題設條件轉變成比較熟悉與典型的模型或問題,實現化生為熟,合理變形與轉化.常見的有化實際問題為數學問題,化幾何(或代數)問題為代數(或幾何)問題,化代數問題為三角問題,等等.

例4(2022年高考數學新高考Ⅱ卷·12)(多選題)對任意x,y,x2+y2-xy=1,則( ).

A.x+y≤1 B.x+y≥-2

C.x2+y2≤2 D.x2+y2≥1

審題：結合題設條件,直接判斷不等式成立問題,涉及較多的不等式性質等,對思維與能力的要求較高.而根據條件中的二元方程加以配方處理,轉化為兩代數式的平方和為1的形式,引入三角參數進行轉換,化代數問題為三角問題,化陌生為熟悉,即可順利進行分析與判斷.

解析：由x2+y2-xy=1,配方可得

故選擇答案:BC.

5 環節五:深入挖掘條件,注意隱含信息

審題時往往需要對題設條件進行必要的再加工,進而深入挖掘條件,特別是其中隱含的一些信息、注意點及其他一些細節等,為問題的正確突破與求解掃清障礙.

審題：結合題設條件,有一些解題者采用“極端思想”,通過題目中側棱長的兩個端點值來快速分析與求解,確定與之對應的答案,導致出錯.解題時要合理挖掘條件,注意側棱長l的變化與該正四棱錐體積變化之間的隱含關系,構建關系式來分析與處理.

解析：如圖1,在正四棱錐P-ABCD中,頂點P在底面ABCD內的射影為點M,球心O在直線PM上,設球O的半徑為R.

圖1

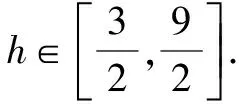
故選擇答案:C.

著名數學教育家波利亞說過:“最糟糕的情況是學生沒有弄清問題就進行演算和作圖.”從這個意義上講,高考數學謀試在“審”,成試在“審”,一點都不過分[2].