如何利用角平分線巧作輔助線

胡蓮

在一些幾何問題中，常常出現有關角平分線的條件，能否恰地當利用角平分線巧作輔助線，往往成為解題的關鍵.下面舉例說明如何利用角平分線作輔助線，來解答有關線段或者角的數量關系問題.

一、作垂線

當題目的已知條件中出現角平分線的時候，我們立刻想到它的性質定理：1.把已知角平分為兩個相等的小角；2.角平分線上的點到角的兩邊的距離相等.因此，經過角平分線上任意一點作角的兩邊的垂線后，可以根據角平分線性質找到全等三角形，然后得到相等的邊長和角度．

例1

證明

二、截取相等線段

當證明題中有角平分線時，常在角的兩邊截取相等的線段，構造全等三角形或等腰三角形，得到一些相等的線段和角度.運用這種作輔助線的方式解題，有截長和補短兩個方向，即延長短的線段或在長的線段上截取一部分使之等于短的線段.無論延長還是截取都要證明線段的相等，進而達到所證目標.

例2

解法一

解法二

三、作平行線

當題目中有角平分線時，常過角平分線上的一點作角的一邊的平行線，因為角平分線有兩角相等，平行線則有內錯角相等，則必然得到等腰三角形；或通過一邊上的點作角平分線的平行線與另外一邊的反向延長線相交，從而也可構造出等腰三角形來解題.結合角平分線去添加平行線的方法應針對具體圖形和問題來分析．

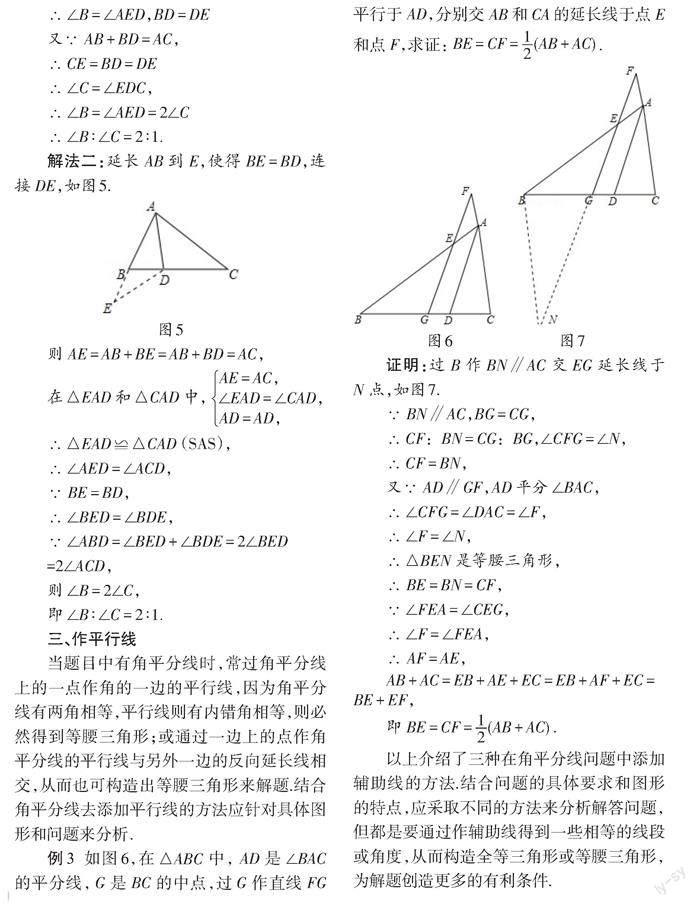
例3

證明

以上介紹了三種在角平分線問題中添加輔助線的方法.結合問題的具體要求和圖形的特點，應采取不同的方法來分析解答問題，但都是要通過作輔助線得到一些相等的線段或角度，從而構造全等三角形或等腰三角形，為解題創造更多的有利條件.