抽象函數問題的類型與求解方法
■彭恒彪
由于抽象函數表現形式抽象,對數學思維能力考查的起點較高,使得這類問題成為函數內容的難點之一。下面介紹抽象函數的常見類型與求解方法。
聚焦1:“賦值法”求抽象函數的值
賦值法就是根據題目的具體情況,合理、巧妙地對某些元素賦予確定的特殊值(0,1,-1等),從而使問題獲得簡捷有效的解決。
例1 已知y=f(x)+3x2的圖像關于原點對稱,若f(2)=3,函數g(x)=f(x)-3x,則g(-2)的值是____。
解:因為y=f(x)+3x2的圖像關于原點對稱,所以f(-x)+3(-x)2=-[f(x)+3x2],即f(-x)=-f(x)-6x2。令x=2,則f(-2)=-f(2)-6×22=-3-24=-27。在g(x)=f(x)-3x中,令x=-2,則g(-2)=f(-2)-3×(-2)=-21。
評注:構建g(-2)與已知f(-2)的關系,利用y=f(x)+3x2的圖像關于原點對稱得到f(-x)=-f(x)-6x2,通過賦值得到f(-2),最后得到g(-2)。
聚焦2:“賦值法”探究抽象函數的奇偶性
判斷抽象函數的奇偶性的關鍵是得到f(x)與f(-x)的關系,解題時要對有關變量進行賦值,使其最后只保留f(x)與f(-x)的關系。
例2 已知定義在R 上的函數f(x)滿足f(x+y)=f(x)+f(y),且f(2)=1,試判斷此函數的奇偶性。
解:令x=y=0,由f(x+y)=f(x)+f(y),可 得f(0)=f(0)+f(0),所 以f(0)=0。令y=-x,由f(x+y)=f(x)+f(y),可得f(0)=f(x)+f(-x)=0,所以f(x)=-f(-x),所以此函數是偶函數。
評注:要得到f(x)與f(-x)的關系,首先對x,y賦值,可得f(0)=0,再對x,y賦值,可得f(x)=-f(-x)。
聚焦3:利用“配湊法”證明抽象函數的單調性
配湊法就是通過恰當的拼與湊,使問題明了化、簡單化,從而達到比較容易解決問題的目的。配湊法的實質是一種迂回的解題方法,體現了轉化與化歸思想。配湊法證明抽象函數的單調性是利用題設條件,結合單調性的定義進行轉化求解的。
例3 定義在R 上的函數f(x)滿足:對任意實數m,n總有f(m+n)=f(m)·f(n),且當x>0時,0 賦值法求抽象函數的解析式,首先要對題設中的有關參數進行賦值,再得到函數解析式的某種遞推關系,最后求得函數的解析式。 評注:其實,本題也可換一種思維方式,對于關系式f(a+b)=f(a)+f(b)+ab,令a=1,得到f(b+1)與f(b)的關系,由a,b都是自然數,得到f(n+1)-f(n)=n(n∈N),這實質上就是一種數列的遞推公式。 解抽象函數不等式,可利用函數單調性的定義,如“已知函數f(x)是增函數,若f(x1) 有些抽象函數是以基本函數為背景抽象而得的。解題時,若能從研究抽象函數的背景函數入手,根據抽象函數的有關性質,通過類比,猜想出它可能為某種基本函數,再由具體函數的圖像與性質來解決抽象函數問題,則可達到事半功倍的效果。 例6 設定義在R 上的函數f(x),對于任意x,y都有f(x+y)=f(x)+f(y)成立,且f(1)=-2,當x>0時,f(x)<0。 (1)判斷f(x)的奇偶性,并加以證明。 (2)試問:當-3≤f(x)≤3 時,f(x)是否有最值? 如果有,求出最值;如果沒有,說明理由。 解:對于任意x,y都有f(x+y)=f(x)+f(y),可猜想抽象函數f(x)的原形函數為f(x)=kx,當x>0時,f(x)<0,可得k<0。猜想如下:函數f(x)是奇函數,函數f(x)在R 上是減函數。 (1)令x=y=0,可得f(0)=0,令y=-x,可得f(0)=f(-x)+f(x),所以f(-x)=-f(x),所以f(x)為奇函數。 (2)設-3≤x1 當x=-3時,f(x)有最大值f(-3)=-f(3)=-f(2+1)=-[f(2)+f(1)]=-[f(1)+f(1)+f(1)]=6;當x=3 時,f(x)有最小值f(3)=-6。 評注:在解答抽象函數問題時,若能尋找出抽象函數的模型函數,根據模型函數的圖像與性質,找出問題的解法或證法,是一種行之有效的好方法。
聚焦4:“賦值法”求抽象函數的解析式

聚焦5:“定義法”解抽象函數不等式

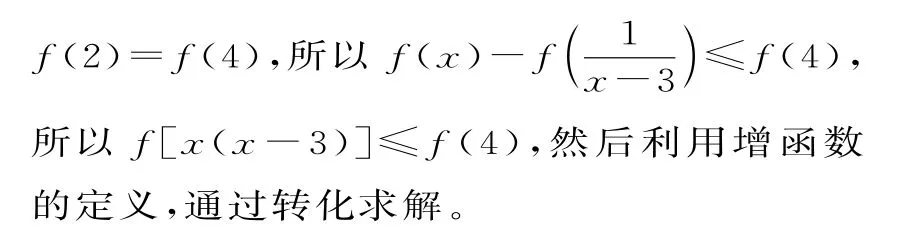
聚焦6:構造初等函數,求解抽象函數問題

