多級評分認知診斷題組模型*

周文杰 童望望 郭 磊，2**

（1.西南大學心理學部，重慶 400715；2.中國基礎教育質量監測協同創新中心西南大學分中心，重慶 400715）

1 引 言

當前傳統測驗領域僅提供籠統的測驗總分或學生能力值來衡量學生的學業水平，但隨著對教育評估要求愈加精細，這種傳統測驗形式已不能滿足人們對評估的需求。因此，心理教育研究者不斷深入認知診斷測評（cognitive diagnostic assessment，CDA）研究，使其既可報告個體具有的認知結構或對知識的掌握情況，也便于教育者為學生進行更客觀、更有針對性的教育評價，并為教育補救指明方向。

在各種大型測驗中，如高考、TOEFL、PISA 等，常存在多個題目隸屬于一個共同刺激的情況，如閱讀理解、完形填空、選詞填空等。這種一組題目共用一個刺激或材料的集合稱為題組（testlet）（Wainer &Kiely，1987）。使用題組有較多優勢：閱讀材料能被充分利用，不僅節約作答時間提高作答效率，還能節約成本（DeMars，2012；Huang，2013）；由于題目隸屬于相同刺激，使得題目結構更復雜，相關性與邏輯性更強，就能測量被試更高層次思維能力（Haladyna，1992）。例如，圖1 是一道考察“確定平面圖中物體的位置的方法”（屬性1）和“線段比例尺的應用”（屬性2）的六年級數學綜合題，該題目有兩個小題，考生在作答過程中受到材料的共同刺激，因此這兩個小題屬于一個題組結構，題目（1）考察了屬性1，滿分為3 分，題目（2）考察了屬性1和屬性2，滿分為4 分。這是一個典型的帶有題組結構的多級計分題目。

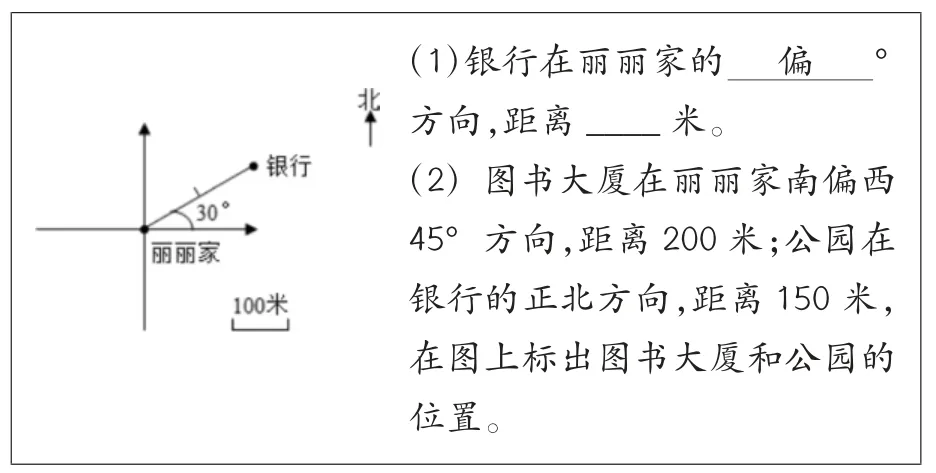
圖1 六年級數學能力測試例題

在項目反應理論（item response theory，IRT）的領域中，研究者提出了多種處理題組結構的方式，其中具有代表性的方法有：（1）視同一個題組下的題目具有雙重維度特性，一個維度是題組效應，一個維度是題目自身的效應，例如二階模型（second-order mode）（Rijmen，2010） 和雙因子模型（bi-factor model）（Demars，2006；Li et al.，2005）；（2）將題目得分合成為題組得分，把同一個題組的題目看作一個多級評分題目（Wainer & Kiely，1987；Rosenbaum，1988）；（3）將題組效應視為影響反應結果的潛變量，例如題組反應模型（testlet response models，TRM）（Bradlow et al.，1999）等。第一種處理方法具有較強的限制，僅能處理當題目只具有一層題組結構時的情況。第二種方法則會導致信息丟失，能得到題組得分，卻不能獲得被試精確的作答結果，且測驗信度會被低估（Yen，1993）。第三種處理方法更靈活地表征了題組內的局部依賴性，獲得更精確的參數估計結果，且具有較好的拓廣性，可以處理多維題組的情況，是目前最常見的方式，本研究即采用該方法處理題組效應。

認知診斷領域中，詹沛達等人（2015）提出了能處理題組效應的認知診斷模型，后續結合反應時模型提出聯合題組認知診斷模型（Zhan et al.，2018），Hansen（2013）結合2-tier 模型（Cai，2010）和LCDM 也提出了一種適用于認知診斷測驗的題組模型。但這些模型只適用于二級評分數據，無法處理多級評分數據。而實際上，心理、教育及社會學等領域中存在大量多級評分題型，如簡答題、材料分析題、Likert 量表等，尤其我國許多測驗二級和多級評分題目經常混合使用（涂冬波等，2010），若采用二分模型擬合多級評分數據，會造成信息丟失（Ma&de la Torre，2016）。另外，雖然研究者已開發多種多級評分診斷模型，如Sequential GDINA 模型（Ma et al.，2016）、一般化多級評分認知診斷模型（General Polytomous Diagnosis Model，GPDM）（Chen & de la Torre，2018）、一般化分部評分認知診斷模型（General Partial Credit Diagnostic Model，GPCDM）（高旭亮等，2019）等，但是均不能處理題組效應。可以看出，目前能夠處理題組數據的診斷模型不適用于多級評分數據，而已有的多級評分診斷模型不能處理題組效應，多級診斷模型與題組反應模型仍處于獨立研究階段。

綜上所述，本研究擬將多級評分診斷與題組效應融合，開發多級評分認知診斷題組模型（Polytomous Cognitive Diagnosis Testlet Model，PCDTM）。本文首先介紹PCDTM 開發過程；其次介紹馬爾可夫鏈蒙特卡洛算法（Markov chain Monte Carlo，MCMC）參數估計內容；第三，使用模擬研究探究模型參數返真性；第四，使用實證數據檢驗模型生態效度。最后總結研究結果，展望未來研究發展方向。

2 多級評分認知診斷題組模型的開發

2.1 多級評分認知診斷模型（GPCDM）簡介

GPCDM 由高旭亮等（2019）提出，是一種以飽和模型GDINA 作為加工函數開發的多級評分認知診斷模型。GPCDM 用公式可描述為：

式中a1=（al1，al2，…，alk，…，alK）為被試屬性掌握模式，l=1，…，L，L=2K。alk為屬性掌握模式為a1的被試在第k 個屬性掌握情況，若被試掌握第k 個屬性，有alk=1，否則alk=0。qjx=（qjx1，qjx2，…，qjxk，…，qjxK）為第j 題第x 分屬性考察情況，若考察了第k 個屬性，則qjxk=1，否則qjxk=0。P（Xj=x）為屬性掌握模式為a1的被試在第j 題得x 分的概率。λjx，k為alk主效應，λjx，k′k為alk′和alk的二階交互效應；λjx，12，…，Kjx是掌握所有屬性時對作答產生的效應大小。

2.2 多級評分認知診斷題組模型構建

2.2.1 多維題組效應

圖2（a）表示單維題組效應，除被試能力θ 外，題目3 的作答還受到一個題組影響，且不同題組之間相互獨立；而圖2（b）多維題組測驗中的題目3，4，5 同時受到了兩個題組的影響（魏丹等，2017；詹沛達等，2015）。可見，單維題組是多維題組的特例。

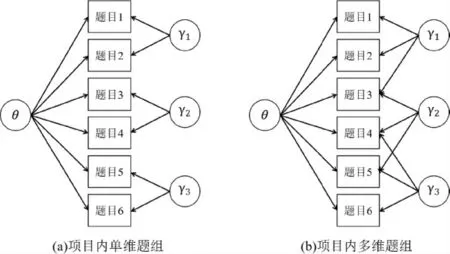
圖2 單維/多維題組示意圖

多維題組效應用公式可以描述為：

公式（2）表示被試i 在題目j 上共受到M 個題組效應的影響。協方差矩陣Σ 表示題組效應大小，Σ=（γi1，…，γim，…，γiM），γim～N（0，），γim表示被試i 在第m 個題組上的效應大小。用判定矩陣U 矩陣表示每個題目在不同題組上的歸屬，其中列表示題組，行表示題目，U=（Uj1，…，Ujm，…，UjM），Ujm表示題目j 是否歸屬于第m 個題組，屬于則Ujm=1，否則Ujm=0。根據判定規則，圖2（b）的題組效應可用圖3 表示。

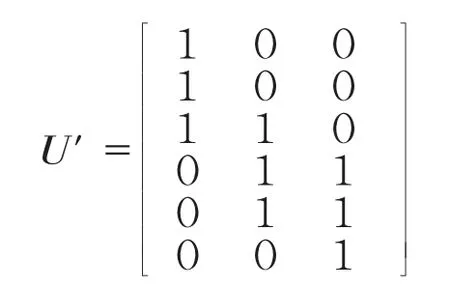
圖3 U 矩陣示意圖

2.2.2多級評分認知診斷題組模型（PCDTM）

進一步結合多維題組和多級評分結構，見圖4（a）表示二級評分的多維題組結構，圖4（b）表示多級計分的多維題組結構，mj表示第j 題的滿分，可以發現在多級計分題組結構中，被試屬性掌握模式α 影響所有的題目作答，同時題組效應γ 可以影響同一個題組中不同題目在不同得分的作答，從而進一步區別題組效應在不同得分水平的影響。為使多級評分認知診斷模型能有效處理題組效應，本研究在GPCDM基礎上引入多維題組效應參數，得到了多級評分認知診斷題組模型（PCDTM），其函數表達式為：

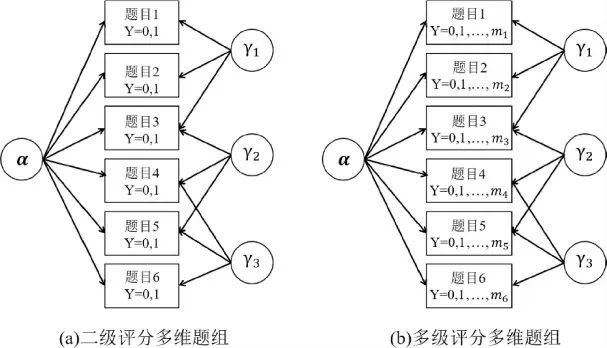
圖4 二級/多級評分多維題組示意圖

3 參數估計

研究采用R 語言R2jags 包，調用MCMC 算法進行參數估計，設定每種實驗條件循環30 次，每次循環設定鏈數為3，每條鏈長5000，間隔數5，預熱前2000 次，取后3000 次參數收斂結果平均數為該鏈參數估計結果。若所有被估計參數的小于1.1 或1.2，則參數基本收斂（Brooks&Gelman，1998）。參考Zhan 等（2019）設置，設定待估計參數的先驗分布為：λjx0～N（-1.096，4），λjx，k～N（0，4）I（λjx，k＞0），λjx，k′k～N（0，4），alk～Bernoulli（0.5），γim～N（0，），～invGam（1，1）。PCDTM 模型代碼已上傳https://doi.org/10.6084/m9.figshare.21581331，供讀者參考和使用。

4 模擬研究

4.1 研究設計

模擬研究使用模型對比的方式，分別以PCDTM 和GPCDM 為真模型，生成有題組和無題組效應作答數據，再分別使用兩個模型擬合數據。研究自變量包括：（1）真模型（GPCDM，PCDTM）；（2） 樣本量（500，1000，2000）；（3）題目質量（高，低）；（4）題目數量（20，40 題）。

4.2 類別Q 矩陣與U 矩陣設定

類別Q 矩陣（Category-Q，Cat-Q）和U矩陣間附表1 和附表2 所示（40 題Cat-Q矩陣與U 矩陣為20 題重復）。在Cat-Q 矩陣中，共考察了5 個屬性，每個得分類別最多考察2 個屬性，且每個屬性考察次數相同。測驗中第1～11 題為三級評分題目，第12～15 題為四級評分題目，第16～20 題為二級評分題目。測驗包含四個題組結構，題組1 包含第1～11 題，題組2 包含12～15 題，題組3 包含16～20 題，3 個題組分別有部分題目包含于題組4，構成項目內多維題組結構。

表1 被試判準率PCCR/AACCR 值

4.3 模擬過程

4.3.1 被試參數設置

被試屬性從伯努利分布中隨機生成，即alk～Bernoulli（0.5），alk＞0.5 取1，alk≤0.5則取0 從而得到不同屬性掌握模式。

4.3.2 題目參數與題組效應設置

參考Ma 等人（2016） 和高旭亮等（2019）的生成方法，將高質量題目參數設置為：logit｛gx［P（Xj=x | a1=0）］｝從均勻分布U（0，0.25）中隨機生成，logit｛gx［P（Xj=x |a1=0）］｝從均勻分布U（0.75，1）中隨機生成；低質量題目參數設置為：logit｛gx［P（Xj=x | a1=0）］｝從均勻分布U（0，0.4）中隨機生成，logit｛gx［P（Xj=x | a1=0）］｝從均勻分布U（0.6，1）中隨機生成。

4 個題組效應滿足多元正態分布，γ～MVN4（0，Σ），題組效應方差取值=0.25，=0.5，=0.75，=1（Wang & Wilson，2005），對角矩陣如下所示：

4.3.3 模擬作答

將被試及題目參數真值帶入公式（1）和公式（3），計算被試在第j 題得x 分的作答概率P（Xj=x | a1），被試在該題最終作答結果根據對應概率大小進行抽取。

4.4 評價指標

使用均方根誤差（root mean square error，RMSE） 和相對偏差的絕對值（the absolute of relative bias，ARB）作為題目參數和題組參數評價指標。平均屬性判準率（average attribute correct classification rate，AACCR）考察屬性返真性；屬性模式判準率（pattern correct classification rate，PCCR）作為屬性掌握模式返真性評價指標。以上指標是認知診斷研究中常見的參數估計精度的評價指標（詹沛達等，2015；Ma et al.，2016；Chen&de la Torre，2018）。

4.5 模擬研究結果

4.5.1 被試判準率返真性

表1 為被試判準率返真性。當真模型為GPCDM 時，PCDTM 與GPCDM 的判準精度非常相近，二者的PCCR 值最大差異僅為0.003，AACCR 最大差異為0.001。當真模型為PCDTM 時，PCDTM 明顯優于GPCDM，二者PCCR 最大差異0.094，AACCR 最大差異0.021。這說明，當存在題組效應時，PCDTM 可以更準確地對被試進行判別。

當存在題組效應時，自變量中，題目質量的影響最大，樣本量的影響最小。具體而言：①題目質量越高，被試判準率越高。在各題目質量條件下，PCDTM 判準精度均優于GPCDM，隨著題目質量提高，使得兩個模型判準精度均有較大提高，PCCR 最大可分別提高12.5%和12.3%。②隨著題目數量增多，兩個模型判準率均有所提高，但PCDTM 對題目數量變化更敏感，PCDTM的PCCR 最大可提升17%，GPCDM 最大僅為12.7%。在低質量條件下，隨著題目數量的增加，兩個模型判準率差距也隨之增大，PCDTM 模式判準率大幅度提高，均維持在0.9 以上；而在高題目質量條件下，不論題目數量如何變化，PCDTM 始終有著較高判準率。③隨著樣本量增加，PCDTM 模型判準率也在穩步提升，PCCR 從［0.748，0.918］提高至［0.766，0.974］。

4.5.2 題目參數返真性

附表3 為題目參數返真性。整體上，當真模型為GPCDM 時，PCDTM 可以達到與GPCDM 相近的題目參數估計精度；而當真模型為PCDTM 時，GPCDM 參數估計精度要明顯差于PCDTM。當GPCDM 為真模型時，兩個模型題目參數估計精度大致相同。當PCDTM 為真模型時，GPCDM 的RMSE和ARB 整體增大，題目參數估計精度大幅度降低，而PCDTM 有較高的題目參數估計精度，且隨著樣本量、題目質量、題目數量的提高，估計精度進一步提高。其中，樣本量影響最大，其次是題目質量，題目數量影響相對較小，GPCDM 題目參數返真性卻出現混亂的情況。

表3 實證研究模型擬合結果

4.5.3 題組效應估計結果

圖5 和圖6 分別為PCDTM 為真模型時（即存在題組效應）和GPCDM 為真模型時（即不存在題組效應時）時，PCDTM 的題組效應參數返真性。整體上PCDTM 具有較小的估計偏差，隨著樣本量、題目數量的提高，對題組效應參數估計精度進一步提高，并且PCDTM 能較好識別沒有題組效應的情境，結果表明PCDTM 模型在各種情境下均能較好地估計題組效應參數。

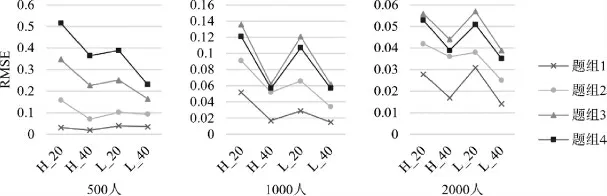
圖5 PCDTM 為真模型時，PCDTM 的題組效應參數誤差均方根（RMSE）

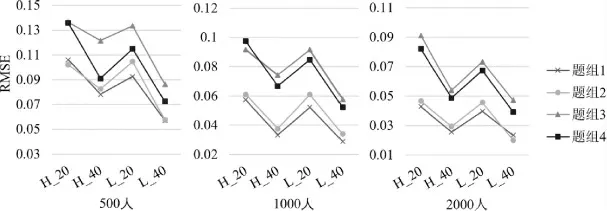
圖6 GPCDM 為真模型時，PCDTM 的題組效應參數誤差均方根（RMSE）

綜上所述，當GPCDM 為真模型時，GPCDM 和PCDTM 判準率和題目參數估計精度差異較小；當PCDTM 為真模型時，PCDTM 判準率和題目參數估計精度明顯優于GPCDM，且有較好的題組效應參數估計結果，而GPCDM 估計精度大幅度降低，且估計結果還出現混亂情況。因此，PCDTM診斷能力更佳，更具普適性。

5 實證研究

5.1 研究目的

分別使用PCDTM 與GPCDM 模型分析2012 年數學大規模測評數據，探查二者在實際數據應用中的效果。該測驗為二級與多級評分題目混合，共114 題，考察了9476 名學生的三個數學認知屬性：數與代數、空間幾何與概率統計（魏丹等，2017），Cat-Q 矩陣見附表4。其中，測驗有7 個題組，Testlet7 中5 個題目又分別屬于其他5個題組中，形成項目內多維題組效應，加粗的題目即構成項目內多維題組效應（如表2 所示）。

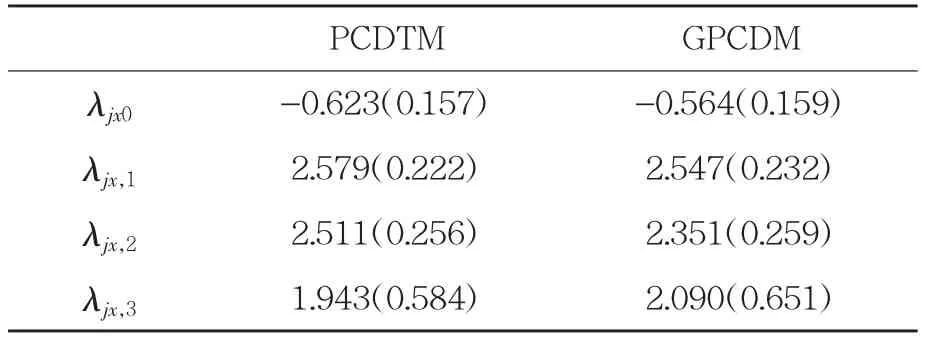
表4 題目參數估計均值（括號內為估計標準誤）

5.2 評價指標

使用MCMC 參數估計中常用的偏差信息量準則（Deviance information criterion，DIC）擬合指標來評價模型在實證數據中的擬合效果。

5.3 研究結果

5.3.1 模型與測驗整體擬合度比較

表3 為模型擬合結果。由結果可知，PCDTM 的擬合指標更小，數據擬合更優，表明在包含題組結構的測驗中，更適合用PCDTM 進行分析。PCDTM 對七個題組效應方差的估計結果為=0.001，=0.507，=0.639，=0.397，=0.498，=0.846，=1.071。其中，第一個題組效應非常小，該題組可能不存在，其余6 個題組對該數學測驗產生中等或高程度的題組效應。正是由于GPCDM 忽視了該測驗的題組效應，導致模型擬合偏差增大。

5.3.2 題目參數估計均值比較

表4 為兩個模型對實證研究題目的截距項和主效應項的參數估計均值及標準誤。其中λjx0為截距項，λjx，1，λjx，2和λjx，3分別為三個屬性的主效應參數。結果顯示，相比于GPCDM，PCDTM 的題目參數估計的標準誤更小，表明PCDTM 模型估計的可靠性更高。

整體而言，PCDTM 模型與實證數據的擬合情況更好，題目參數估計結果更佳，是處理帶題組測驗的優勢模型。

6 研究結論與討論

6.1 研究結論

本文將多維題組隨機效應參數引入多級評分認知診斷模型中，成功構建了PCDTM 模型，并得出以下結論：

（1）PCDTM 合理有效，無論測驗是否含有題組效應，均能得到精確的參數估計結果。隨著樣本量、題目質量、題目數量增加，被試判準率、題目參數與題組效應參數估計精度均有所提高。

（2）忽視題組效應，會降低題目參數估計精度和被試判準率，甚至出現估計結果混亂的情況。

（3）實證研究中，PCDTM 模型擬合更優，參數估計精度更高，是處理題組數據的優勢模型，值得推廣。

6.2 討論與展望

6.2.1 PCDTM 適用性

整體而言，PCDTM 模型具有較好的參數估計表現，對無題組效應的作答數據也能達到與GPCDM 相近的精度，同時對有題組效應的作答數據，PCDTM 模型擬合效果更佳，參數估計精度也更高。這是因為PCDTM 模型對局部依賴性進行表征，將其視為影響作答結果的另一種影響因素，不僅能有效處理題目間存在的依賴性，還能減少了模型的系統誤差，提高了模型對數據的擬合程度，從而提高對被試能力和題目參數估計的精確性。

6.2.2 PCDTM 使用建議

模擬研究中，題目質量對判準率影響最大，樣本量影響最小；樣本量對題目參數影響最大，其次是題目質量。當樣本量增多，題目參數表現情況更好，若想得到較精準的參數估計結果，又保證運行效率，建議樣本量不低于1000。高題目質量時，參數估計精度均較高，低題目質量時，即使樣本量增加，判準率也較低，此時通過提高題目數量，參數估計精度便能大幅度提高。因此，在實際應用時樣本量至少1000 人；題目質量較低時，題目至少40 題。

6.2.3 研究展望

未來研究可從以下方面探索：（1）本研究是以分部評分思想構建模型，未來可基于不同建模思想，構建豐富的多級評分題組模型；（2）項目功能差異檢驗（differential item function，DIF）是衡量測驗公平性的重要指標，而目前基于題組模型的DIF 檢驗方法大多基于CTT 或IRT，也需要適合認知診斷的題組DIF 檢驗方法；（3）多項選擇題（Multiple-Choice，MC）常以題組形式出現，雖已有對MC 題診斷方法的研究（Di-Bello et al.，2015；Liu&Liu，2021；郭磊，周文杰，2021），卻未處理存在的題組效應，未來也需開發合適的診斷模型。