基于可移動全雙工接收機的隱蔽通信容量魯棒優化*

許 睿，李高磊，李建華

（上海交通大學，上海 200240）

0 引言

無線通信的移動性和動態性雖然拓展了信息傳輸的渠道和范圍，但也增加了網絡管理和資源分配的難度，需要高額的代價增加安全防護能力。另外，電磁波的開放特性使得信息在傳輸過程中很容易受到非法用戶的攻擊和竊取，無線網絡中的電磁干擾、環境噪聲也會導致傳輸信號的失真和泄露。可以看出，移動通信中存在的各類不穩定性因素給信息安全傳輸帶來了極大的威脅和挑戰。為了保證通信行為的可靠穩定，彌補物理層安全領域的諸多不足，隱蔽通信技術應運而生。

文獻[1]引入了全雙工接收機輔助的隱蔽系統，為后續的研究搭建了諸多輔助框架。文獻[2]討論了竊聽方在獲取信道分布信息時，接收機干擾功率對傳輸性能的影響。文獻[3]從信號發射概率著手，在多層衰落信道下對系統容量展開分析。文獻[4]和文獻[5]重點研究了多輸入多輸出（Multiple-Input Multiple-Output，MIMO）系統中發射功率的魯棒性優化問題，文獻[6]和文獻[7]則分別評估了認知系統中信道狀態信息對帶寬分配的影響。文獻[8]討論了無限信道使用數的隱蔽通信中全雙工接收機AN 功率和傳輸效能之間的關系。文獻[9]和文獻[10]構建了廣播模型下的隱蔽傳輸體系，并針對其可靠性進行驗證。在此基礎上，文獻[11-15]針對不同通信場景引入了不同的輔助通信節點，完成了對應隱蔽方案的設計，文獻[16-18]則討論了大規模中繼組網中隱蔽系統的可行性。鑒于實際應用中可用信道數大多是有限的，文獻[19]主要探討了延遲受限系統的隱蔽性能。在此基礎上，文獻[20]對具有有限塊長度（即有限數量的信道使用）的系統進行信道估計，驗證了隨機功率發射算法的穩定性優勢。

總之，現有研究多集中在基礎模型的擴展及隱蔽容量的分析等方面，而較少有關于隱蔽節點位置信息的研究。基于此，本文在竊聽方位置信息未知的前提下，構建了一種基于可移動全雙工接收機的隱蔽通信模型，通過對全雙工接收機的空間位置和功率不確定性范圍進行魯棒優化，確保在合法鏈路進行信息傳輸的有效性和可靠性。

1 系統模型

1.1 隱蔽通信基礎模型

隱蔽通信系統結構如圖1 所示，該系統由合法發射機Alice、合法接收機Bob 和惡意竊聽方Willie這3 個通信節點組成。本文中，全雙工接收機Bob可以在接收Alice 發送信號的同時，發射一定功率的干擾噪聲（Artificial Noise，AN），以干擾Willie的檢測行為。

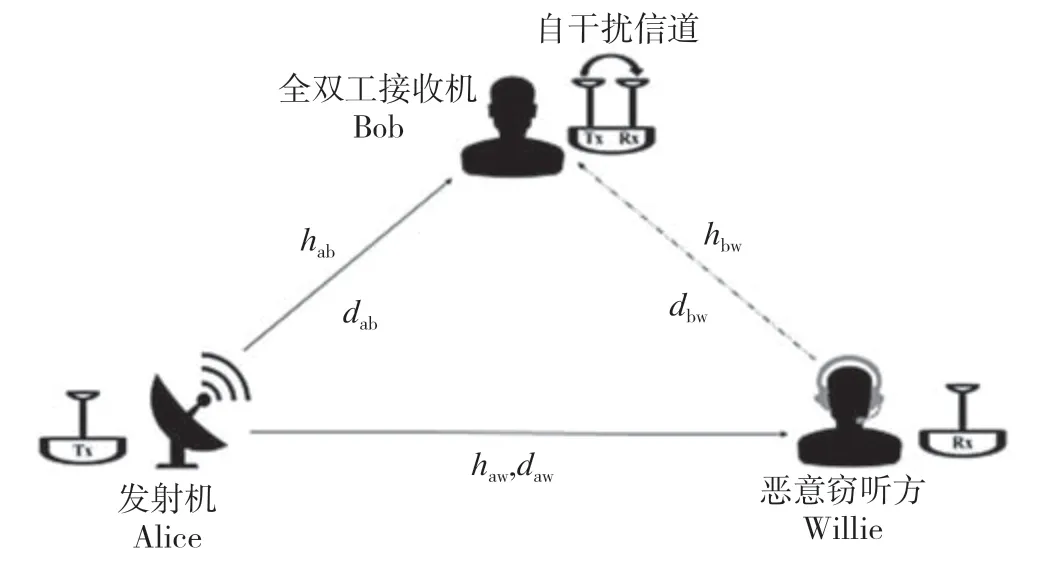
圖1 全雙工接收機的隱蔽通信系統模型

式中：ew為相對位置誤差，為圓形UZ 區域的圓心。同時，假定Bob 的部署區域DZ 也是一個以rb為半徑的標準圓形區域，則其坐標可以寫成：

在瑞利衰落信道中，接收機利用隨機干擾技術進行信息壓制，干擾功率在不同的傳輸時隙間隨機變化，即Bob 的干擾機發射功率Pb的概率密度函數滿足如下關系：

式 中：ΣP=[PU,PL]為 功 率 不 確 定 范 圍（Power Uncertainty Range，PUR）。PU和PL分別對應干擾AN 功率的不確定范圍的上下界，且0 ≤PL≤Pb≤PU≤，為全雙工接收機的最大干擾功率。

1.2 竊聽方的假設檢驗分析

本節就Willie 的最優檢測性能展開分析，假設各節點間衰落信道的信道系數分別為haw，hab，hbw。由于全雙工接收機天線在進行干擾壓制時存在自干擾，本文以hbb表示其自干擾信道系數。由于系統中Bob 的干擾功率遠大于Alice 的發射功率，故若合法鏈路進行傳輸行為，則接收機處收到的信號為：

式中：α為路損系數，λ(0≤λ≤1)為自干擾消除系數，sa[·]和sb[·]分別為標準傳輸信號和標準干擾信號的強度。由二元信號假設檢驗理論，Willie 處的接收信號強度可表示為：

式中：H0和H1分別對應Alice 和Bob 是否進行通信的兩種情況；vw[n]是以為方差的高斯白噪聲信號。假設上述信道均為準靜止瑞利信道，根據Neyman-Pearson 準則，即可得到最小檢測誤差下的系統最優判決表達式為：

式中：γ為傳輸功率檢測門限，Ns為采樣樣本的信道數目，*為采樣信號卷積，PFA和PMD分別為Willie 的虛警概率和漏檢概率，D0和D1分別為虛警假設和漏檢假設。在可用信道數趨近無窮的前提下，式（6）可進一步表示為：

根據魯棒優化的思路，竊聽方需選取最優的閾值以最小化自身的錯誤檢測率，根據式（8）即可得到：

式中：P為統計概率。

1.3 隱蔽模型的性能指標

根據1.2 節的分析，若從最優檢測的角度進行系統分析，則竊聽方檢測閾值應滿足：

此時對應的最優檢測概率即為：

接收方信噪比可寫成：

此時傳輸鏈路的中斷概率為：

式中：Rab和Cab分別代表預設吞吐量和系統瞬時速率。本文在未有信道衰落的情況下對后續信道行為展開分析，若竊聽方處于最優檢測條件，則對應的錯誤概率為：

在此基礎上，以有效隱蔽吞吐量作為系統傳輸性能的評判，其表達式為：

2 問題建模與分析

在前文的分析基礎上得出，須在滿足所給隱蔽約束及位置約束條件下，最大化合法通信鏈路的隱蔽吞吐量。故系統優化問題可表示為：

式中：C1 為隱蔽性能約束，ε為約束性參數；C2表示全雙工接收機干擾功率約束；C3 為Willie 和Bob 的分布區域約束；D1 和D2 分別為Bob 的可部署區域DZ 和Willie 的可分布區域UZ。下面就該問題展開魯棒分析，首先對η關于PL進行一階求導：

可見，η隨著PL的增大而逐漸減小，故系統的最佳AN 下界功率PL=0，因此可將C1 進一步轉換為通信節點間的距離約束：

定義等號成立時的最大dbw為rCE，將式（10）做進一步轉換可以得到：

定義以Willie 實際分布位置為圓心、C1 為半徑的區域為隱蔽可行區（Covert-Enable Zone，CEZ）。當Bob 位于CEZ 內部時，可同時滿足約束條件C1 和C2。在此基礎上，本文進一步定義CEZ和DZ 的重疊區域為隱蔽重疊區（Overlap Zone，OZ），當Bob 位于OZ 內部時，合法通信鏈路方可實現正向的隱蔽傳輸。觀察Bob 和Willie 之間的位置分布關系，可得到：

將式（18）進一步轉換為：

隨后對η關于PU進行一階求導：

故η與PU呈負相關關系，當式（21）滿足取等條件時，傳輸過程可實現的最大有效隱蔽吞吐可表示為：

對式（22）關于dab進行求導計算可得：

將該結果回代式（22）和式（18），則可以得到實現系統最大隱蔽吞吐量的AN 功率上界為：

3 仿真結果分析

仿真環境設置為：瑞利信道背景噪聲功率為-104 dBm，AN 自干擾消除系數λ=0.01，隱蔽約束常數ε=0.2，預設吞吐量Rab=1 bit，路徑損耗系數α=2，發射機信號功率Pa=0.5 W。發射機Alice、接收機Bob、竊聽方Willie 的初始分布位置分別為[0,15]m、[8,20]m、[25,25]m。

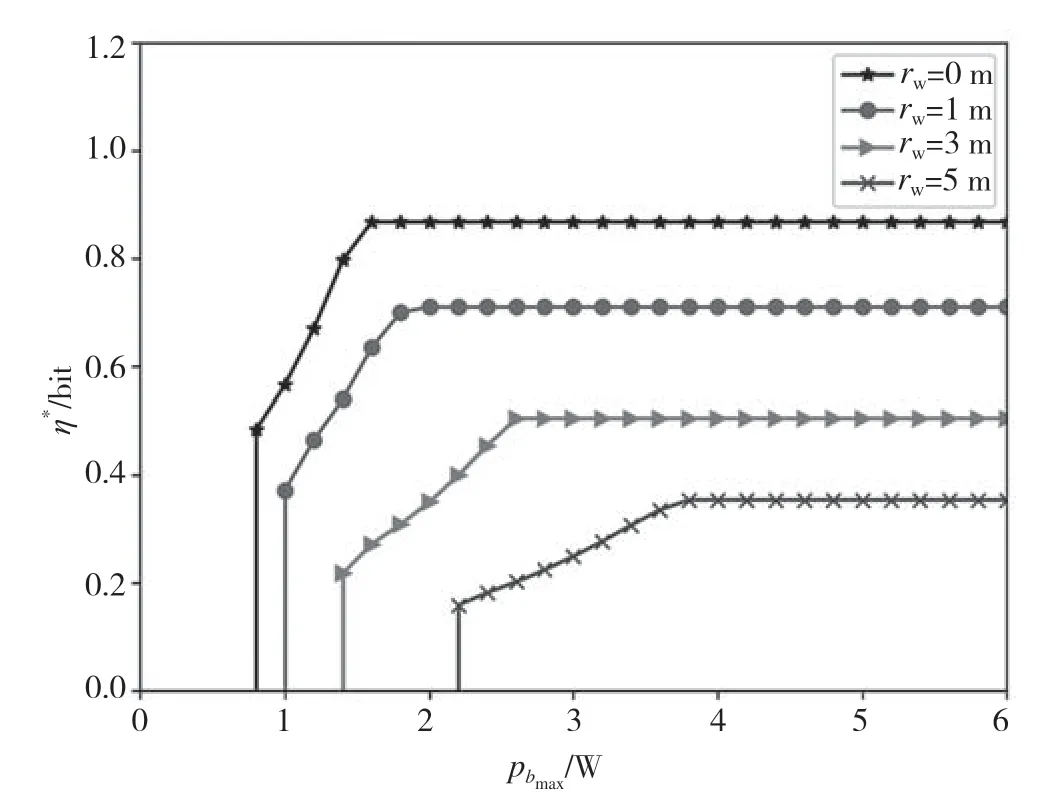
圖2 最大AN 功率與系統最大可實現吞吐量的關系

圖3 顯示了可部署區域DZ 范圍同最大有效吞吐量η*之間的關系，可以看出η*隨著DZ 半徑rb的增大而增大，這是因為隨著可部署區域的擴大，全雙工接收機有更大的概率部署至距離發射機更近的點位上，這同前文的分析結論相一致，即η*會隨著dab的增大而逐漸減小，因此在竊聽方位置范圍未知的情況下，應該盡可能地擴大DZ 范圍以滿足通信鏈路的隱蔽約束。

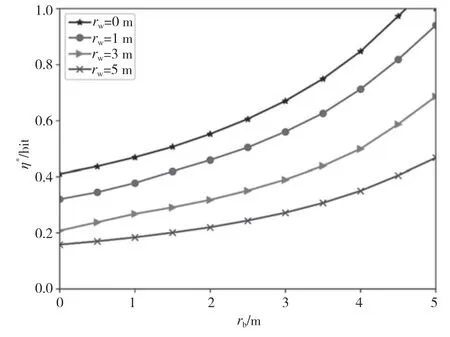
圖3 可部署區域半徑與系統最大可實現吞吐量的關系

如圖4 所示為干擾AN 功率上界PU對實時有效吞吐量η的影響，η隨著PU的增大而呈現出先上升后下降的變化趨勢，這是由于初始階段PU的增大會導致重疊區域范圍也隨之擴張，直至PU=P2，AN 功率達到臨界狀態，Bob 恰好以最小的AN 功率部署在最佳點位上，此時即可實現全雙工接收機的最優部署。然而，隨著PU繼續增大，Bob 的部署位置不再發生改變，過高的干擾功率對信息的有效傳輸帶來了負面的影響，造成了通信資源的浪費，因此需針對特定場景選取合適的PU設計隱蔽系統。

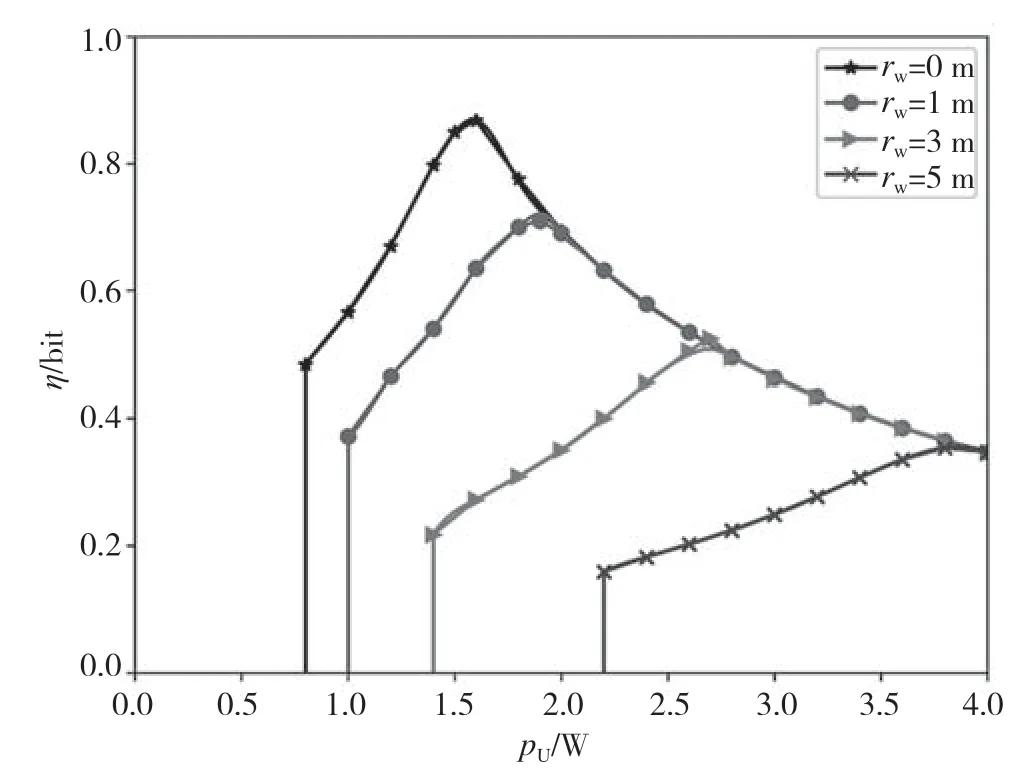
圖4 AN 功率上界與系統有效吞吐量的關系

4 結語

本文研究了一種基于可移動全雙工接收機的隱蔽通信系統，以實現未知竊聽方確切位置場景下的信息可靠傳輸。首先，根據傳輸中斷概率推導出Willie 的最優檢測條件，并以此為基準構建出聯合優化框架；其次，通過動態調整Bob 的干擾功率及部署位置，在滿足隱蔽約束的條件下最大化合法鏈路的有效隱蔽吞吐量，并結合仿真結果分析了DZ范圍和最大AN 功率對系統傳輸性能的影響。今后，將考慮融合低延時信道、多干擾節點等復雜場景，形成更具系統性、實踐性的隱蔽通信模型。