混合邊界約束下矩形薄板自由振動問題的有限積分變換解*

李逸豪, 徐 典, 陳一鳴, 安東琦, 李 銳

(大連理工大學 工程力學系 工業裝備結構分析優化與CAE軟件全國重點實驗室, 遼寧 大連 116024)

0 引 言

彈性矩形薄板廣泛應用于土木工程、海洋工程及機械工程等領域,其力學行為一直是學者們的研究重點之一[1-4]．其中,彈性薄板的自由振動問題因其與結構安全高度相關而備受關注,此類問題的解析求解對于結構的快速分析和初步設計具有重要意義．針對板的自由振動問題,其核心是在滿足給定的邊界條件下,通過求解該問題的高階偏微分控制方程來獲得板的固有頻率和振型．然而,由于高階偏微分控制方程求解過程的復雜性,相關邊值問題的解析求解成為一類難題．傳統解析方法,例如Navier解法[5]和Lévy解法[6]只能求解對邊簡支約束下的板問題,其余邊界條件下的矩形薄板自由振動問題都不易獲得解析解．

實際工程應用對于板的邊界約束提出了更高的要求,一邊受到混合約束(即同時存在固支、簡支或自由中的兩種或以上約束)的板進入學者們的視野．例如,在汽車制造領域廣泛應用的邊緣點焊鋼板[7]就是一種典型的混合邊界約束板,其點焊位置在分析時可等效為固支邊界條件,而同一邊上其余位置仍然可視為簡支等邊界條件．然而,對于這類復雜約束下板的振動問題,傳統方法更難以解析求解．針對上述情況,學者們通常采用數值方法來解決相關問題,例如有限元法[8-9]、有限條法[10]、有限差分法[11-12]、邊界元法[13-14]、微分求積法[15]、微分容積法[16]等．

上述各類數值方法可以得到滿足工程需要的結果,但是解析解仍然具有重要的地位．首先,解析解具有獨特的研究價值,例如:其可以作為經驗公式以及數值方法對比的基準、快速參數分析和優化的工具,同時也可以為實驗提供理論依據等．此外,數值方法所求結果通常為近似解,未必總能達到高精度要求,且求解輸入量和輸出量較多,過程比較復雜．因此,發展解析方法不僅對理論方法的發展和完善具有重要價值,也對工程結構分析與設計具有重要的指導意義．基于上述背景,本文擬尋求一種新的解析方法來處理混合邊界約束下矩形薄板的自由振動問題．

有限積分變換法作為求解數學物理方程的一類重要方法,近年來被筆者等進一步發展,用于板殼力學一般問題的解析求解[17-23]．該方法的思路是:將待求問題的控制方程轉換到積分變換域內,得到含有待定系數的位移函數變換式,再由邊界條件求解待定系數,最后通過積分逆變換可得到原問題的解析解．因有限積分變換法簡潔有效,更容易被工程師所理解和接受,因此有望作為一種通用的理論分析工具．然而,以往關于有限積分變換法的研究均聚焦一邊僅有單一約束的問題,對于一邊受到混合約束的問題則未能直接應用該方法．為此,有必要將有限積分變換法進一步發展,推廣至混合邊界板問題的求解中．

本文將有限積分變換與子域分解法結合,首次實現了混合邊界矩形薄板自由振動問題的解析求解．首先根據混合邊界條件將矩形板拆分為兩個子域,然后應用有限積分變換法對兩部分分別解析求解,最后通過滿足子域間的連續性條件得到該問題最終的解析解．限于篇幅,本文聚焦工程中典型的邊緣點焊懸臂板的自由振動問題,將其歸結為一邊固支-簡支混合約束、其余三邊自由的矩形薄板自由振動問題進行求解．數值算例表明,無論是固有頻率還是振型,本文的結果均與精細有限元及文獻結果高度吻合,求解結果的精度不亞于其他復雜的解析方法．本文方法及相關結果有望作為檢驗各類數值方法精度的對比基準,求解思路也可推廣至其他復雜邊界約束下的板殼力學問題．

1 薄板自由振動問題的控制方程

基于Kirchhoff薄板理論,矩形薄板自由振動問題的控制方程如下:

(1)

式中W(x,y,t)表示t時刻的撓度;D=Eh3/[12(1-μ2)]表示抗彎剛度,其中E為彈性模量,h為板的厚度,μ為Poisson比;ρ表示薄板密度．根據振動理論,板在自由振動時的動撓度方程為W(x,y,t)=w(x,y)sin(ωt),其中w(x,y)為振型函數,ω為固有頻率．將W代入式(1),得到矩形薄板振型微分方程如下:

(2)

板的內力可由w表示為

(3)

其中Mx和My表示Oy軸向和Ox軸向的彎矩,Vx和Vy表示垂直于Ox軸和Oy軸的橫截面中的等效剪力．

2 混合邊界約束下矩形薄板自由振動問題的有限積分變換解

針對混合邊界矩形薄板,本文以“C”“S”“F”分別表示固支、簡支、自由這三種邊界條件,并從左下方邊界開始以順時針方向通過字母對板命名．限于篇幅,本文以工程中典型的邊緣點焊懸臂板、即CS-F-F-F型混合邊界矩形薄板為對象進行求解．如圖1所示,板的尺寸表示為a,b,b1及b2,其中b=b1+b2;坐標軸Ox與Oy分別與板的下邊界與左邊界重合．

圖1 撓曲電納米板模型及其坐標系Fig. 1 The flexoelectric nanoplate model and its coordinate system

圖1 CS-F-F-F型混合邊界矩形薄板圖2 CS-F-F-F型混合邊界矩形薄板各子域示意圖Fig. 1 The rectangular thin plate under CS-F-F-F Fig. 2 Schematic diagram of the sub-domains of CS-F-F-F-F mixed boundary constraints rectangular thin plates

將原板按照邊界條件拆分為①、②兩個子域,即將原問題拆分為兩個子問題,隨后對兩個子域分別采用有限積分變換法進行求解,在求解過程中每個子域需要滿足相應的邊界條件及內部連續性條件．各子域的幾何模型如圖2所示．

圖2 撓曲電納米矩形板的邊界Fig. 2 The boundary of a flexoelectric nanorectangular plate

對于每個子域,在矩形域0≤xi≤a,0≤yi≤bi內定義二維有限余弦積分變換如下:

(4)

式中i表示子域編號1、2,wi和(xi,yi)分別表示子域的位移函數和局部坐標,α(m)=mπ/a,βi(n)=nπ/bi,其中m=0,1,2,…,n=0,1,2,…．

逆變換的表達式如下:

(5)

上式中當m=0時,ε(m)=1;當m=1,2,…時,ε(m)=2;當n=0時,ε(n)=1;當n=1,2,…時,ε(n)=2．依據式(4)對式(2)所示高階偏微分方程各相關項進行二維有限余弦積分變換,可得

(6)

(7)

(8)

(9)

由余弦函數的性質可以消去式(8)中的下劃線部分,隨后將式(6)—(9)代入式(2)的變換式,可得

(10)

為方便書寫,記

(11)

(12)

根據式(3)—(5),并結合Stokes變換[24],可得邊界處的彎矩表達式如下:

(13)

(14)

(15)

(16)

同理,可得邊界處等效剪力的表達式如下:

(17)

(18)

(19)

根據圖2可知:子域①需要滿足的邊界條件為

(20)

需要滿足的連續性條件為

(21)

(22)

則子域①的位移函數積分變換式為

(23)

根據圖2可知子域②需要滿足的邊界條件為

(24)

需要滿足的連續性條件為

(25)

(26)

則子域②的位移函數積分變換式為

(27)

綜上,還未滿足的邊界條件和連續性條件有

(28)

(29)

3 典型算例分析

表1 CS-F-F-F方板前十階無量綱固有頻率收斂性研究

表2給出了不同長寬比的CS-F-F-F板在b1=b2條件下的無量綱固有頻率．通過與精細有限元分析(采用ABAQUS軟件中的S4R單元,網格尺寸為0.002 5a)的收斂結果以及文獻的結果對比可知,對于不同尺寸的板,本文的固有頻率解均與參考結果吻合良好,證明了本文求解方法的有效性和求解結果的準確性．圖3給出了CS-F-F-F方板前十階振型,結果也與有限元解高度吻合．

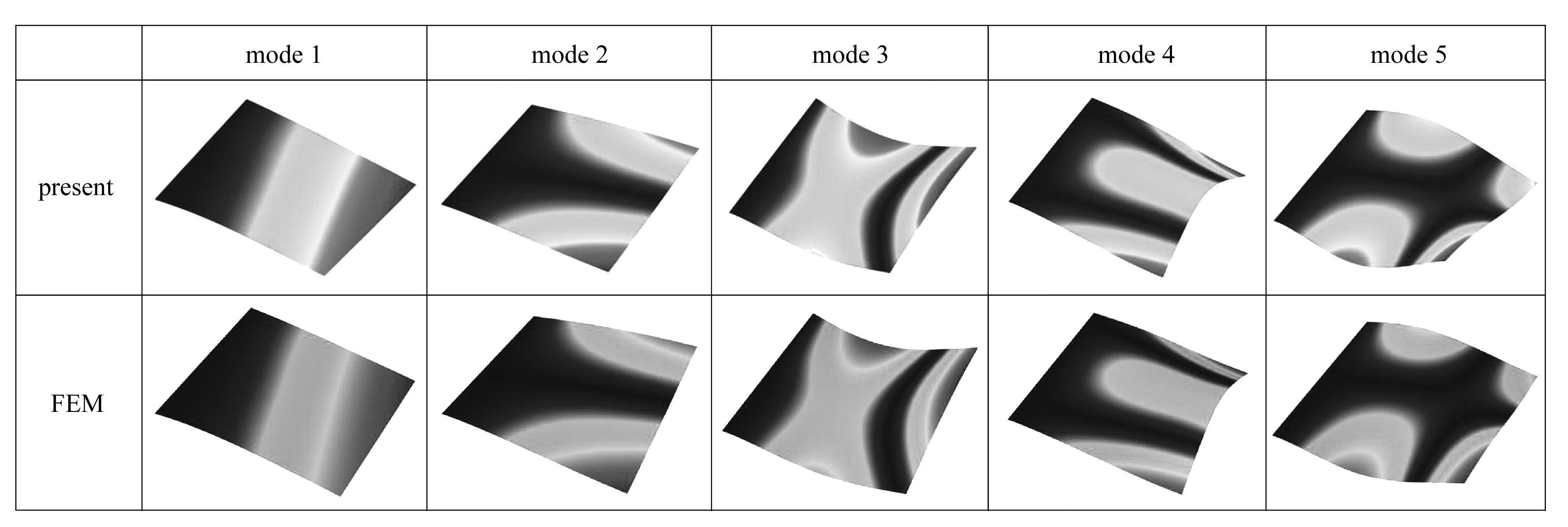
表2 不同長寬比CS-F-F-F板在b1=b2條件下的無量綱固有頻率

圖3 加載區域Fig. 3 The loading area

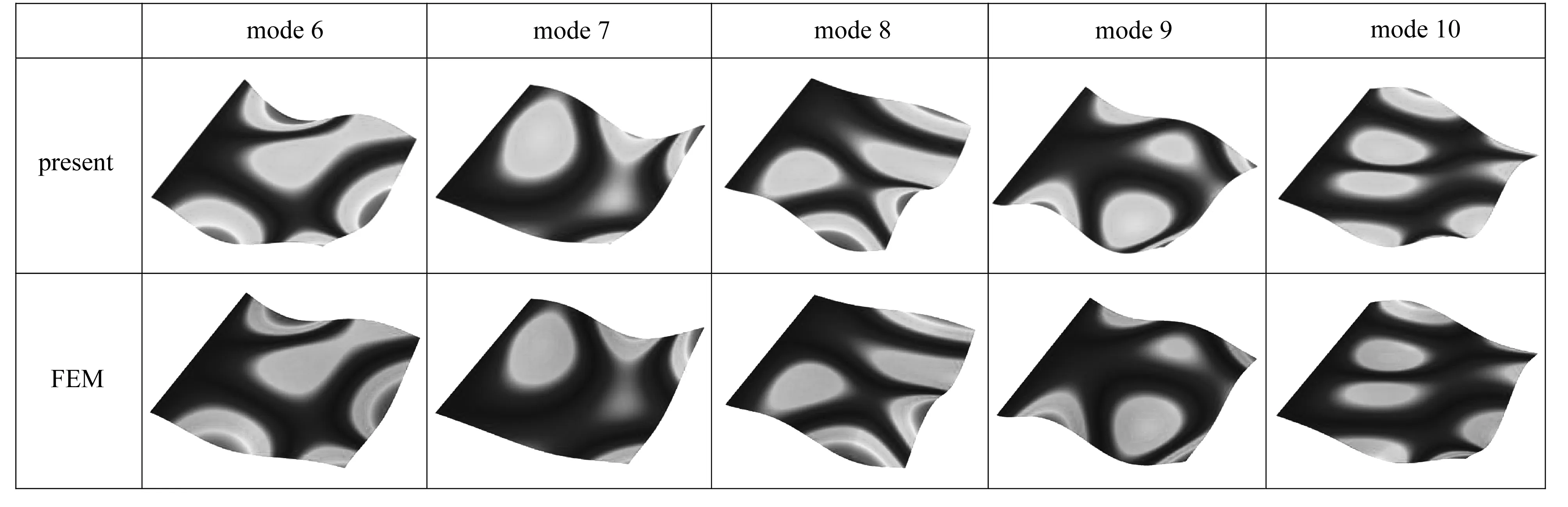
圖3 CS-F-F-F方板的前十階振型Fig. 3 The first 10 mode shapes of CS-F-F-F square plates

4 結 論

本文首次將有限積分變換法擴展至混合邊界約束薄板自由振動問題的解析求解,以工程中常見的邊緣點焊懸臂板為背景,具體求解了CS-F-F-F型板的自由振動問題．分析過程中采用雙余弦形式的積分核對兩個子域分別解析求解,最后通過連續性條件獲得該問題完整的解析解．本文給出的數值算例表明獲得的解析解與精細有限元分析及文獻結果吻合良好,證明了求解方法的有效性及所求結果的準確性,同時為檢驗各類數值方法提供了對比基準．本文發展的有限積分變換結合子域分解的方法在求解過程中無需預先假設解的形式,而是從基本控制方程出發并逐步推導以獲得結果,因此是一種嚴格的求解方法,可為復雜邊界約束下板殼力學問題的解析求解提供一種新思路．