固化黃土力學特性三軸試驗研究

劉忠玉, 朱少培, 張家超, 寧秉正

(鄭州大學土木工程學院, 河南 鄭州 450001)

0 引言

黃土,作為一種特殊土,具有多孔性以及沉陷性等特點,且在我國分布較廣。針對這類土質,大量學者已對其工程性能進行了一系列的研究。其中,黃土的變形及強度問題是不少學者關注的焦點。在這方面,國外較早的研究是由Savvateev[1]開展的。后來,國內劉祖典等[2-3]就陜西關中地區黃土的變形特性進行了探討。自那以后,學者們分別從濕陷性[4-5]、溫度荷載[6]、結構性[7-8]以及干濕循環因素[9-10]等角度入手,探究了影響黃土變形的因素,也相繼提出了不同因素下黃土的應力應變關系[11-13]。上述研究使我們對黃土的基本特性有了較為充分的認識。

為改善黃土的不良工程特性,固化是對黃土進行改良的常用方法之一。其中,郭婷婷等[14]利用粉煤灰對黃土進行了固化,并研究了粉煤灰摻量對固化后土體的壓縮性、滲透性以及強度的影響。吳文飛等[15]利用水泥對黃土進行了固化,研究了水泥摻量對固化土的強度、水穩性以及濕陷性的影響。除了上述固化材料外,有學者[16]提出應用水玻璃固化黃土,即硅化法處理黃土。為了提高該方法對黃土的固化性能,不斷學者也對此進行改進,比如溫度改性[17-18]、電場改性[19]等。然而,上述處理地基的方法各有不足,比如傳統固化劑(比如水泥、粉煤灰等)具有耗能高、污染環境等特點,而硅化法處理地基的成本則比較昂貴。為此,一些學者著手研制新型固化劑,以期改善上述固化劑的不足。例如,王銀梅等[20]、張虎元等[21-22]、彭宇等[23]先后開發出新型高分子(SH)固化材料和抗疏力固化劑,將其應用到黃土固化中,并探討了這些固化劑對黃土的強度、滲透性以及膨脹性的影響。同時,賀智強等[24]、侯鑫等[25]先后從宏觀與微觀的層面入手,探討了木質素對黃土的固化作用。值得注意的是,上述研究中土體取材大多集中于陜甘地區,然而不同地域的黃土性能具有明顯的差異性。當前,為合理規劃黃河流域周邊城市群的發展,國家提出了“黃河流域生態保護和高質量發展”的戰略。因此,研究沿線地區黃土的固化性能對工程建設具有重要意義。

本文以鄭州地區典型黃土為試驗材料,選取某新型固化劑進行固化,利用GDSTTS標準應力路徑三軸儀開展了固化黃土的力學性能研究。這里,筆者主要探討了圍壓、固化劑摻量以及固化土養護齡期對固化土剪切過程應力應變關系的影響。

1 試驗概況

1.1 試驗材料

試驗用黃土取自鄭州某地,取土深度為5 m。經測定,該土密度為2.7 g/cm3,液限為22.9%,塑限為14.7%,塑性指數為8.2,為黃土狀粉土。土壤固化劑選用河南嘉科吉地科技實業有限公司生產的一種新型無機類固化劑,主要由礦渣硅酸鹽水泥、火山質灰硅酸鹽水泥、粉煤灰硅酸鹽水泥以及某種激發劑按照一定的配比摻和而成。

1.2 試樣制備

首先,將試驗用土風干碾碎,并過2 mm篩子去除雜質。然后,將試驗用土與固化劑按照3%、5%、7%、9%、11%摻量進行配制,以含水率為17%進行均勻拌和后,利用分層擊實法制成密度為1.75 g/cm3,直徑為38 mm,高度為76 mm的圓柱形試樣。最后,將試樣放入恒溫恒濕試驗箱,在溫度20±2 ℃,濕度95%條件下養護到試驗所需齡期的最后一天采用真空飽和法將試樣飽和備用。這里養護齡期分別設定為7 d、28 d、60 d、90 d。

1.3 試驗方法

采用GDSTTS標準應力路徑三軸儀對試樣進行CU試驗。首先對試樣進行反壓飽和,直到B值大于0.95。然后設定圍壓分別為50 kPa、100 kPa、200 kPa、300 kPa,當孔壓完全消散后,在不排水條件下施加偏應力直至試樣破壞。

2 試驗結果分析

2.1 圍壓對固化黃土力學特性的影響

圖1給出了摻量3%和5%,7 d齡期的試樣在不同圍壓下軸向應變εd隨偏應力q變化的曲線。很明顯,不同圍壓下固化土的應力應變曲線呈現應變軟化的特征。也就是說,固化土具有明顯的結構性。從圖中也可以發現,圍壓對固化土的峰值應力和殘余強度均有影響,具體表現為,二者會隨圍壓的增大而增大。

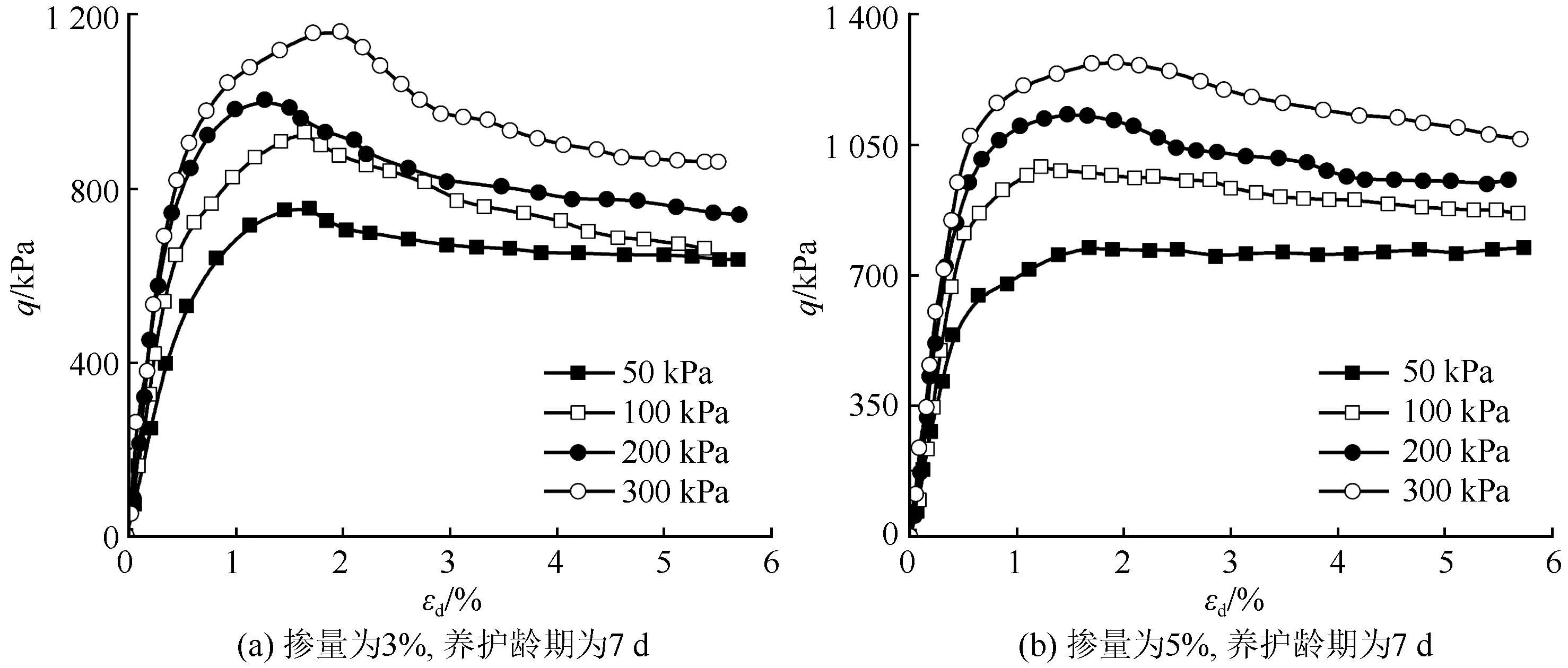
圖1 圍壓對固化黃土偏應力-軸向應變曲線的影響Fig.1 Influence of confining pressure on the deviatoric stress-axial strain curve of solidified loess

2.2 摻量對固化土力學性能的影響

圖2給出了不同摻量的齡期7 d和28 d的固化黃土試樣分別在圍壓100 kPa和200 kPa條件下軸向應變εd隨偏應力q變化的曲線。由圖2可知,固化劑摻量對固化土峰值應力以及殘余應力的影響十分明顯。并且,摻量越大,固化土的峰值應力與殘余強度就會越大。對于這種現象,我們可以這樣理解:當固化劑遇水時,二者會發生化學反應,并形成易與土顆粒結合的水化產物。由于這種產物的存在,土體中的孔隙會大量縮小,進而提高了土體的抗剪強度。

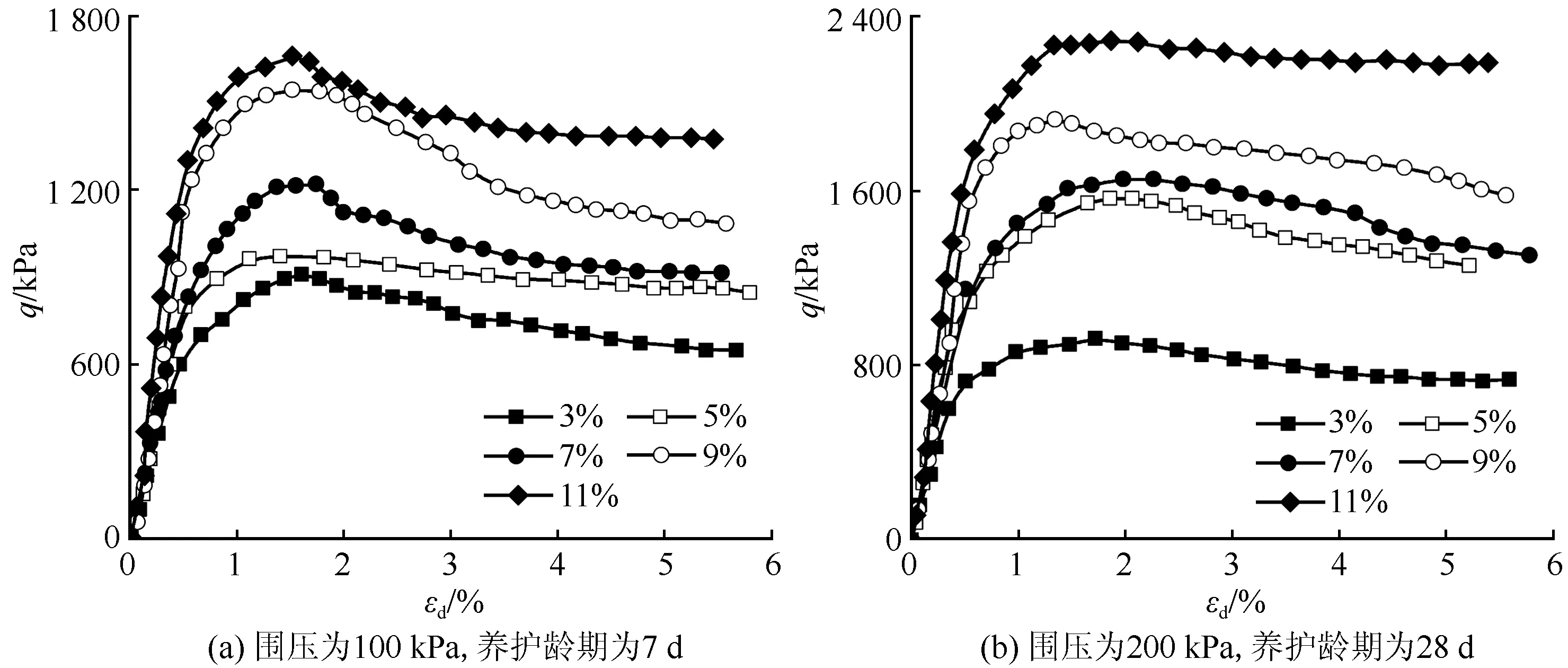
圖2 固化劑摻量對固化黃土偏應力-軸向應變曲線的影響Fig.2 Influence of solidified agent content on the deviatoric stress-axial strain curve of solidified loess

2.3 養護齡期對固化土力學特性的影響

圖3給出了固化劑摻量5%和7%的試樣在200 kPa圍壓下軸向應變εd與偏應力q的關系曲線。圖3表明,隨著齡期的延長,固化土的峰值應力與殘余強度均會增大。這是由于養護時間越長,固化土中的固化劑與水反應越充分,進而提高了固化土的相應強度值。但是,這種增幅并不會隨著齡期的增長而變大。相反,這種趨勢會越來越小。以圖3(a)為例,28 d的峰值應力是7 d峰值應力的1.39倍,而90 d的峰值應力則是60 d相應值的1.09倍。

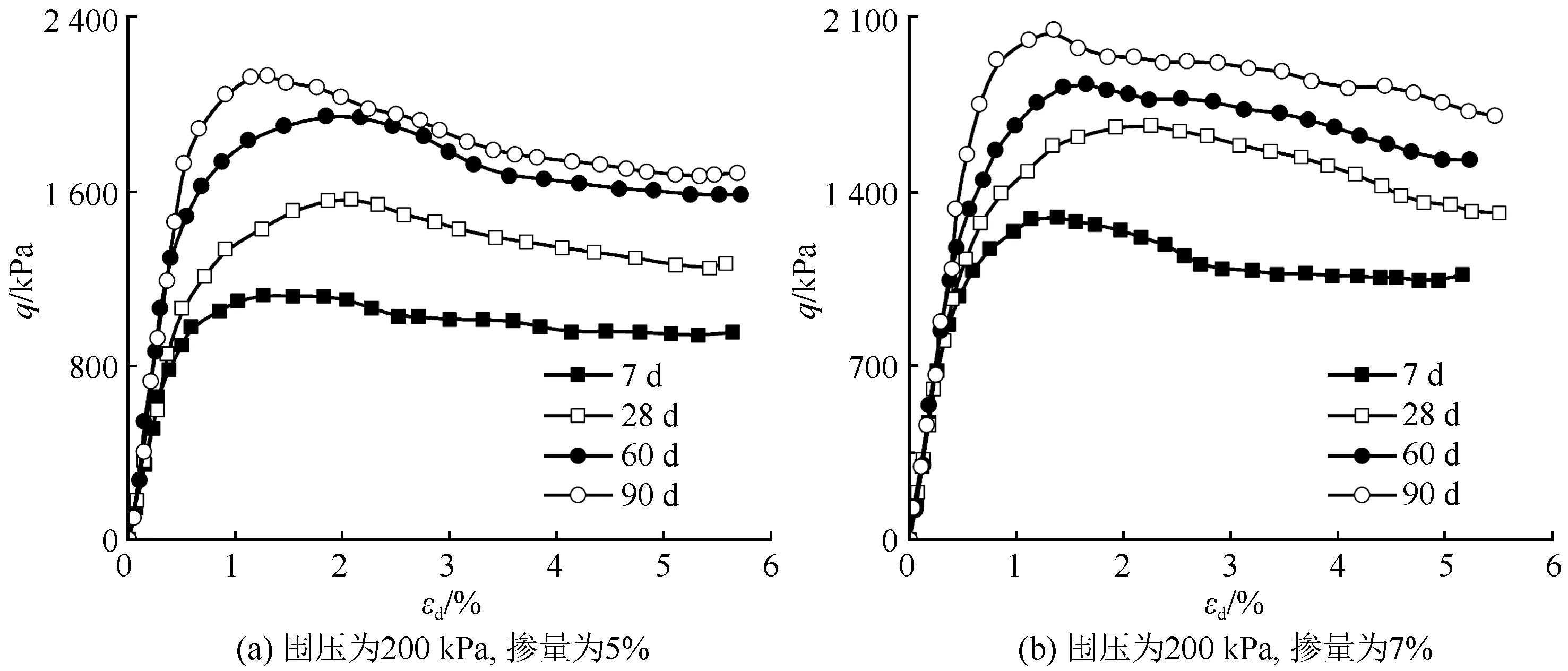
圖3 齡期對固化黃土偏應力-軸向應變曲線的影響Fig.3 Influence of curing age on the deviatoric stress-axial strain curve of solidified loess

產生這種現象的原因,我們可以認為:在養護初期,固化劑與水反應強烈,產生相應的水化產物較多,進而填充土顆粒間的孔隙;而隨著養護時間的增大,這種水化反應會越來越弱,因而相應強度的增加也就不再明顯。

3 固化黃土應力應變關系表達式

上述研究結果表明,固化黃土具有顯著的結構性特征。為描述結構性土的應力應變特征,學者們提出了一系列的本構關系式。其中,沈珠江[26]曾提出一個描述剪切過程的駝峰型三參數表達式:

(1)

式中:a、b、d均為待定參數,它們的單位均為kPa-1。這樣,峰值應力對應的軸向應變εs=a/(b-2d),峰值應力qs=1/[4(b-d)],相應的殘余應力qr=d/b2。

該模型中相關參數物理意義明確,并且能夠利用常規的三軸剪切試驗獲得。為此,筆者采用該模型對本文試驗結果進行擬合。圖4中給出了示于圖1(b)和圖3(a)的試驗結果的擬合曲線,相應的擬合參數示于表1和表2。其中R2最小為0.968,因此該表達式能夠較好地描述固化黃土的剪切過程。

表1 圖4(a)所用參數取值

表2 圖4(b)所用參數取值

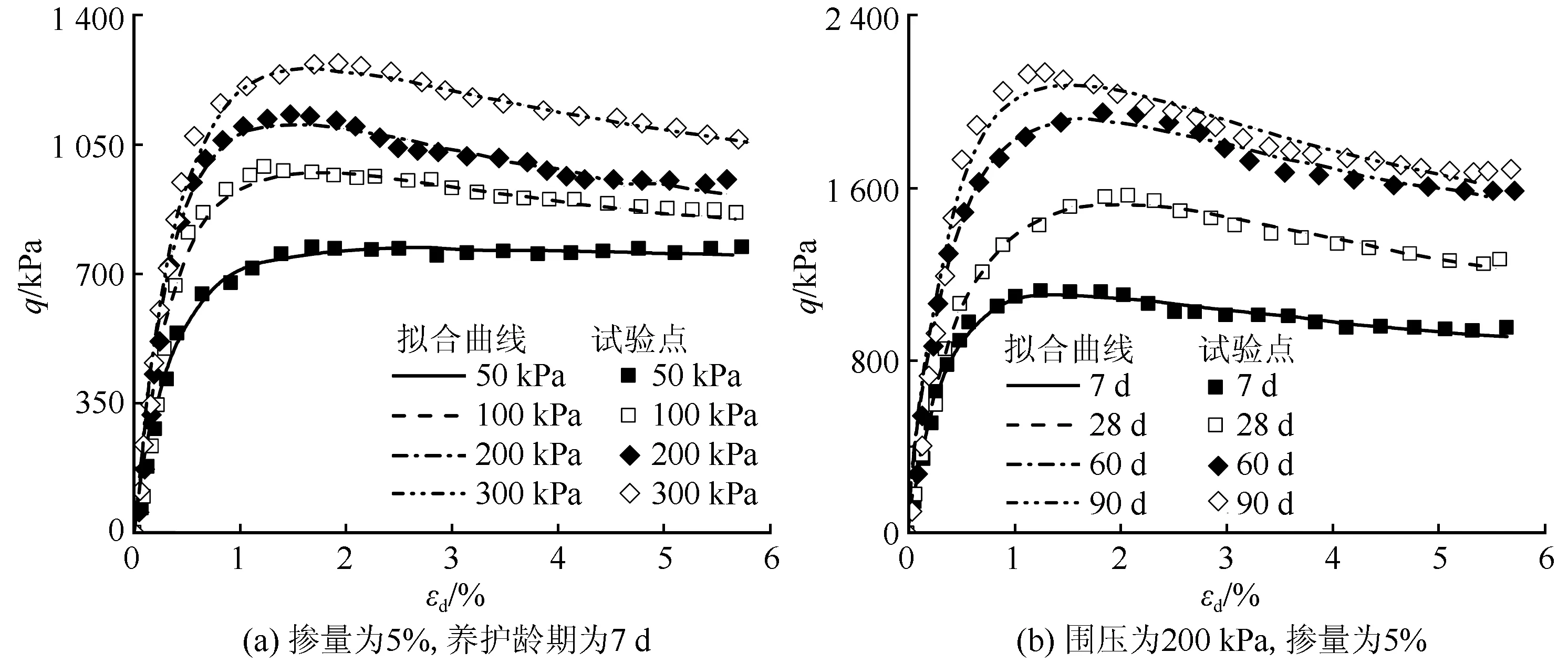
圖4 駝峰型表達式對固化土應力-應變關系的擬合Fig.4 Fitting of stress-strain relationship of solidified soil by hump expression

4 結論

(1) 鄭州地區黃土經固化劑固化后具有顯著的結構性,其應力應變曲線表現出應變軟化特征。圍壓越大,固化劑摻量越多,養護齡期越長,固化土的峰值應力與殘余強度就會越大。

(2) 較之圍壓與摻量,養護齡期對固化土應力應變曲線的影響具有范圍性。當齡期較短時,固化黃土強度隨齡期延長而增長較快;而隨著齡期的延長,齡期對固化黃土強度的影響越來越弱。

(3) 鄭州地區固化黃土的應力應變關系可用駝峰曲線描述。