一種內蘊基線漂移校正的人工地震波反應譜擬合方法

張樹翠, 夏宏升, 張欣剛,, 姚文莉, 齊朝暉, 劉大強

(1. 青島理工大學理學院, 山東 青島 266525; 2. 上海中聯重科樁工機械有限公司, 上海 201613;3. 工業裝備結構分析國家重點實驗室, 遼寧 大連 116024;4. 大連華銳重工集團股份有限公司, 遼寧 大連 116022)

0 引言

擬合匹配目標反應譜的人工地震波是開展重大工程結構非線性時程分析的重要依據之一[1],特別是在對核電樓層反應譜進行擬合時,其“峰多谷深”的特點進一步增大了收斂難度[2-3]。因此,快速高精度擬合真實、合理且匹配目標反應譜的人工地震動仍然面臨很大的挑戰[4]。

目前相關地震動模擬方法主要有時域法和頻域法[5]。以三角級數法[6-7]等為代表的頻域方法能夠保留初始地震動的相位譜[8],且不需要以自然波作為必須條件,因此仍然具有時域方法不可替代的作用。為了提高人工波擬合效率,李建波等[9]提出了一種人工波初篩策略來避免迭代過程陷入某些特定隨機狀況。由于這些擬合算法僅考慮了加速度時程的非平穩性特征,且較少考慮其對速度、位移時程的影響[10],因此在通過兩次積分得到速度、位移時程曲線后還需采用基線校正[11]的手段來消除基線漂移問題。陳三紅等[12]提出在每次迭代時都對所得加速度時程進行基線校正處理,從而避免了時程積分時的基線漂移。Hancock等[13]通過調整小波函數消除了速度和位移時程的漂移,但無法得到封閉的小波系數解。LA Atik等[14]提出了不含位移和速度時程漂移的調整小波函數來得到小波系數的封閉解。張郁山等[15]構造了一種用于校正的增量加速度小波函數,采用該函數積分得到的增量速度和增量位移曲線不出現基線漂移。王體強等[16]提出一種自適應魯棒加速度積分方法并進行可靠度分析,該文獻綜述了10種代表性的加速度積分方法,例如周寶峰等[17]提出的基于Hermit插值和平坦度為判據的加速度積分方法,以及被美國地質調查局(United States Geological Survey,USGS)采用的USGS法[18]等,并對各算法的基線校正原理和特點進行了總結評述。

上述研究的共同特點是:在獲得加速度時程后通常需要進行基線校正處理才能消除位移、速度時程中的基線漂移問題。 既然基線漂移問題在擬合完成后也要被消除,那么如何在擬合過程中就使其自然滿足基線歸零條件是非常值得研究的課題。

結合該研究思路,提出一種內蘊基線漂移校正且匹配目標反應譜的人工地震波直接擬合方法。該方法采用與傳統頻域法相反的思路:首先構造非平穩位移時程表達式,其次求導得到速度與加速度時程表達式,進一步確定使其同時滿足歸零條件的包絡函數,隨后利用單自由度系統諧波響應解析式將目標反應譜匹配問題轉化為與之等價的非線性方程組,利用高效的非線性方程求解算法快速迭代期望幅值,對隨機相位譜的修正來進一步提高擬合精度,最終同時給出滿足歸零條件的位移、速度及加速度時程。數值算例驗證了所提方法的擬合效率和精度。

1 頻域法擬合人工地震波

采用三角級數法擬合人工地震波,并對幅值譜進行迭代使其匹配目標反應譜。該過程簡述如下:

(1) 利用一組具有隨機相位的三角函數構造近似高斯平穩隨機過程:

(1)

式中:Ck為傅里葉幅值譜;φk為隨機相位譜;a(t)是具有零均值和(單邊)功率譜密度函數的高斯平穩隨機過程。傅里葉幅值譜可表示為:

(2)

式中:S(ωk)為功率譜密度函數;Δω為頻域采樣間隔。

標準加速度反應譜與功率譜密度函數的關系為:

(3)

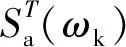
(2) 將平穩隨機過程和考慮非平穩特性的外包線函數做乘積:

(4)

(5)

(6)

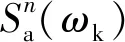
2 內蘊基線校正的直接擬合方法

為使加速度、速度及位移時程自然滿足歸零條件,提出一種與傳統頻域法相反的思路,將非平穩的位移時程u(t)表示為:

(7)

式中各參數的意義與式(4)一致。對上式求兩次時間導數,得到:

(8)

(9)

為了使位移、速度與加速度時程自然滿足歸零條件,可構造在上升段、平穩段以及衰減段平滑過渡的包絡函數,例如:式(7)～式(9)中的強度包絡函數f(t)應當具備或滿足如下條件:(1) 在起始和終止時刻保證位移、速度及加速度函數值為0;(2) 在平穩段包絡函數值為1;(3) 在平穩段的開始和結束時刻應當具備二階連續性。 亦即滿足如下條件:

(10)

為滿足上述光滑條件,在上升段和衰減段,強度包絡函數可以由5次多項式進行表示:

(11)

將式(11)代入式(10)可得:

(12)

(13)

式中:m=T-t2。由此可以解出式(11)中的待定系數,由此得到的包絡函數為光滑的連續函數。強度包絡函數的選擇不唯一,例如式(5)給出的經典包絡函數也可以作為式(7)～(9)中的包絡函數。

結合上述條件,加速度時程函數式(9)在平穩段的表達式可寫為:

(14)

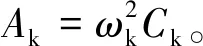
為求解人工地震波反應譜引入如下假設:單自由度系統在人工地震波作用下的最大地震響應發生在強震階段,故可由式(14)求解其最大地震響應,進而獲得人工地震波反應譜。

依據式(14),可將圓頻率為ωj的單自由度系統諧波響應表達式寫為:

(15)

式中:ξ為單自由度系統阻尼比:ωj為第j個單自由度系統的圓頻率。

求出式(15)的復數解可得到單自由度系統的相對位移解xj為:

(16)

(17)

(18)

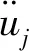
(19)

式中:符號“Imag”表示對復數取虛部。

依據反應譜縱軸的意義,擬合設計反應譜的目標是使下式成立:

(20)

(21)

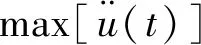
至此,就可將以匹配目標反應譜的人工地震波擬合問題轉化為求解一組以待求幅值譜為迭代目標的非線性方程組[式(20)～(21)]。利用成熟高效的非線性方程求解器,例如MATLAB “fsolve”求解器可快速迭代滿足要求的幅值譜Ak。

上述人工波擬合算法的流程如圖1所示。所提算法具有如下優勢:

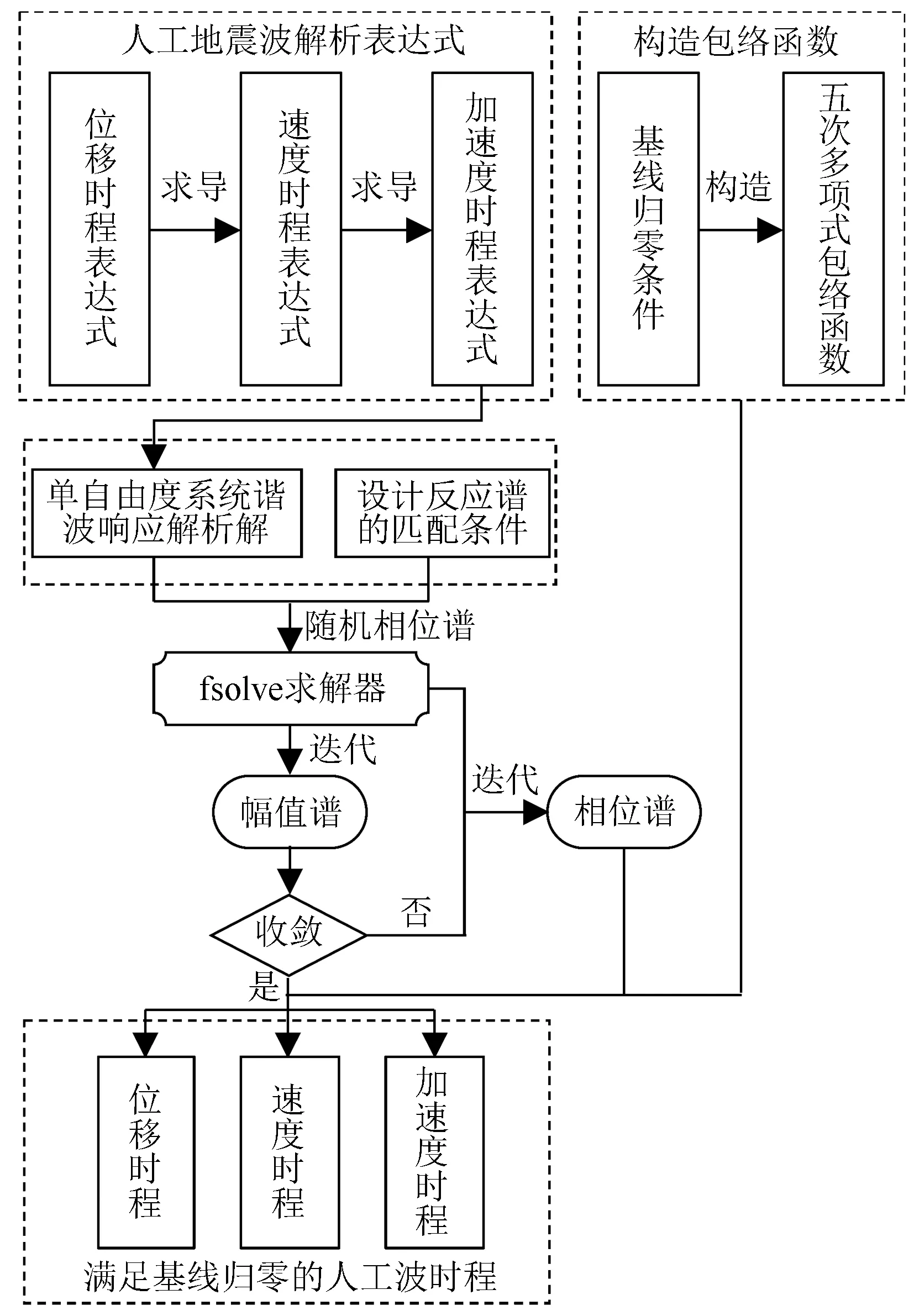
圖1 人工波擬合流程圖Fig.1 Flow diagram for artificial seismic wave fitting

(1) 能夠快速擬合自然滿足基線歸零條件的人工地震波,直接得到位移、速度以及加速度時程;

(2) 不必在得到加速度時程后再構造基線校正算法處理基線漂移問題;

(3) 將匹配目標反應譜的擬合問題轉化為以待求幅值譜為迭代目標的非線性方程,結合高效的非線性方程求解器進行求解,具有編程難度低,收斂精度高的特點,可成為人工波擬合的新途徑。

3 反應譜擬合算例

為驗證所提人工地震波擬合方法的有效性,選擇核電站抗震設計中的Rg1.60標準譜、某核島內41.68 m高度的水平、豎向樓層譜以及《建筑抗震設計規范(GB 50011—2010)》中的設計譜分別作為目標反應譜,并對分析結果的擬合精度、迭代殘差以及擬合效率進行分析。

采用MATLAB “fsolve”求解器進行迭代時,對最大迭代步數“MaxIterations”進行限制以提高迭代效率。具體迭代步驟如下:首先仍然依據標準加速度反應譜與功率譜密度函數的近似關系得到一組幅值譜作為迭代初值帶入求解器迭代15次;隨后以相位譜為目標迭代3次;最后再以幅值譜為目標迭代7次。由于所提方法與考慮迭代相關的擬合方法不同,因此不開展兩者之間的精度對比。

表1給出了擬合精度和收斂耗時情況,圖2給出了3組隨機相位譜下采用Rg1.60標準譜擬合的人工波反應譜,圖2(d)～(f)給出了非線性方程求解器迭代過程中的迭代殘差趨勢。

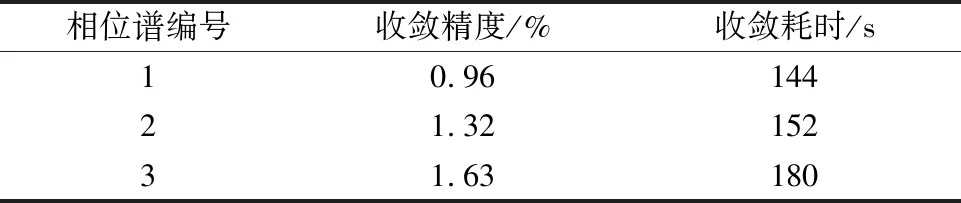
表1 精度與效率比較

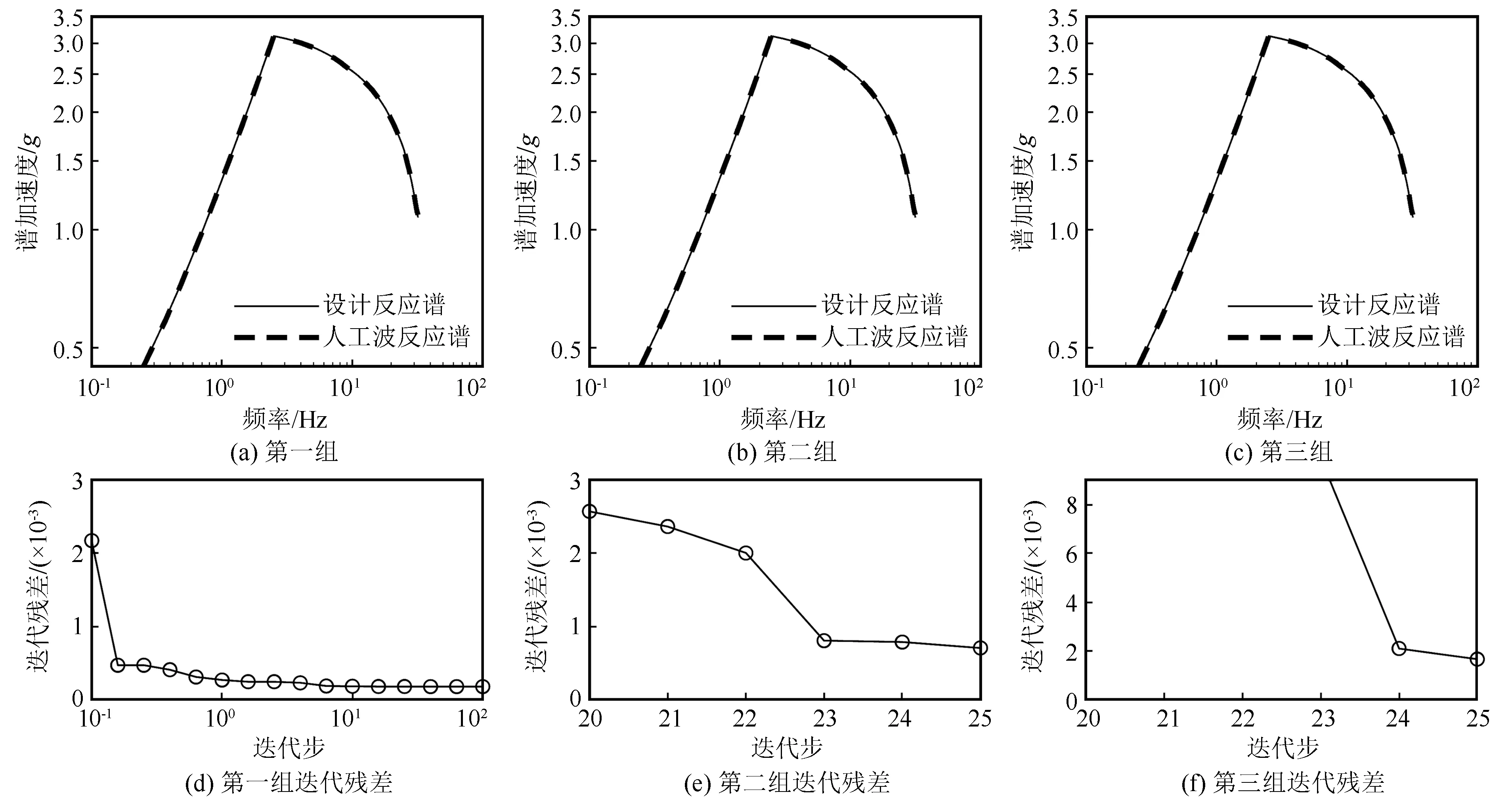
圖2 Rg1.60目標譜擬合結果Fig.2 Fitting results of Rg1.60 target spectrum

由表1可知,所提方法對于3組隨機相位譜均能達到3%以內的高精度要求(70個擬合點),且收斂時間均在5 min以內。在精度和效率方面都達到了預期的擬合要求。

分析圖2結果可見,圖2(a)中第10個迭代步已達到較好的收斂精度。而圖2(b)結果則顯示,在對隨機相位譜進行修正后,繼續對幅值譜進行迭代也達到了預期的精度效果。圖2(c)中的結果表明在最后幾個迭代步達到收斂精度。所提算法在3組隨機相位譜下均達到理想的擬合效果。

從擬合難度來看,Rg1.60反應譜幅值呈線性分布,擬合效果較好。為了驗證所提方法能夠處理目標曲線更為復雜的反應譜擬合問題的能力,采用相對復雜的核電廠樓層譜,采用3組隨機相位譜,所得結果如圖3所示(RRS表示目標反應譜)。核電廠樓層譜曲線在局部具有諸多復雜的“轉折”之處,本文選擇50～60個目標點進行擬合,目標曲線“轉折”的細節有所弱化。圖中結果可見,對于核電廠樓層譜,所提方法在20個迭代步內達到合理的擬合效果。特別是在核廠房基礎結構放大效果的影響下,2%、5%阻尼比的水平方向樓層譜的峰值可達6g～10g,因此在相應的頻段采用加密的頻率點參與擬合后可進一步提高求解器的收斂效果。

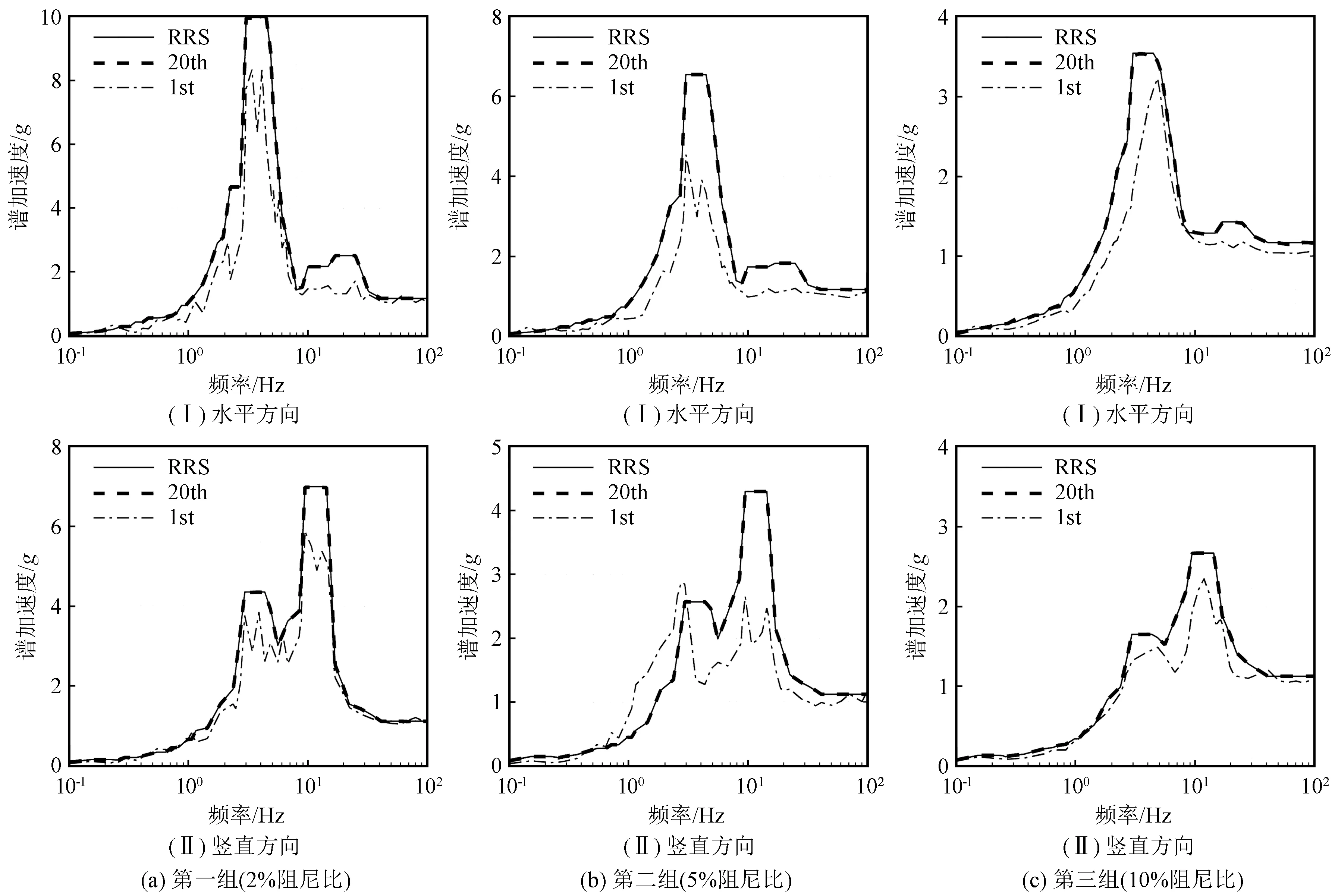
圖3 核電廠樓層譜擬合結果Fig.3 Fitting results of floor spectrum of nuclear power plant

進一步分析不同阻尼比下的擬合結果:采用相同的傅里葉幅值譜初值條件時,2%和10%阻尼比下的擬合效率要比5%阻尼比要高,其原因尚不明確。同時還需說明的是,圖中所示目標反應譜的擬合點數目均在50～60之間,與原反應譜相比復雜程度有所降低。若要充分考慮原反應譜的細節,則擬合點的數目將顯著增大,頑固點相應增多,所提方法的擬合能力需要后續進一步的檢驗和優化。另一方面,圖3采用的核電樓層譜雖然局部細節復雜,但僅有兩個“高峰”,尚不能完全體現“峰多谷深”的特點,后續將開展進一步的相關研究。

最后,采用《建筑抗震設計規范(GB 50011—2010)》規定的反應譜進行擬合,參數為:設防烈度8度,Ⅰ類場地,設計地震分組為2組,特征周期Tg=0.2 s,地震影響系數取αmax=1.06。

圖4同樣給出了3組隨機相位譜下的擬合結果對比。圖中每一列對應一組相同的隨機相位譜,圖4(d)～(f)為高頻部分的局部細節圖,圖4(g)～(i)對應低頻部分的局部細節圖。

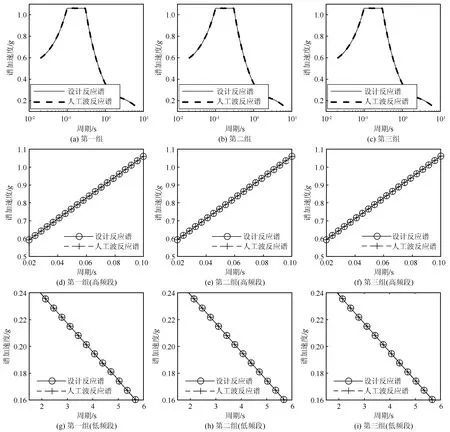
圖4 3組隨機相位譜擬合結果對比Fig.4 Comparison between fitting results of three groups of random phase spectra

由于擬合點的分布較為復雜,因此第一次迭代次數調整為30次,后兩次迭代次數不變。分析結果表明,初次迭代時人工波反應譜和目標反應譜差距較大,但很快趨近目標值。第一次迭代結束時,第一組的高頻段末端仍存在誤差為4%的頑固點,隨后在對相位譜進行5次迭代調整后,頑固點的相對誤差迅速降低到0.82%,達到了較好的收斂效果。

在高頻段,單自由度系統的地震響應近乎剛體運動,一些學者發現采用傳統頻域法在一些特定情況下有時面臨擬合困難的問題[4]。例如對核電站樓層譜進行擬合時,25～100 Hz的頻率段就存在大量的頑固點。所提方法依據單自由度系統諧波響應的解析解,同時采用成熟的非線性方程求解器并結合高效的L-M算法進行迭代,在低頻和高頻段都得到了較好的收斂精度。

圖5給出了采用所提方法得到的人工地震波加速度、速度以及位移時程。由于算法內蘊基線歸零條件,因此各時程曲線均不存在基線漂移問題。

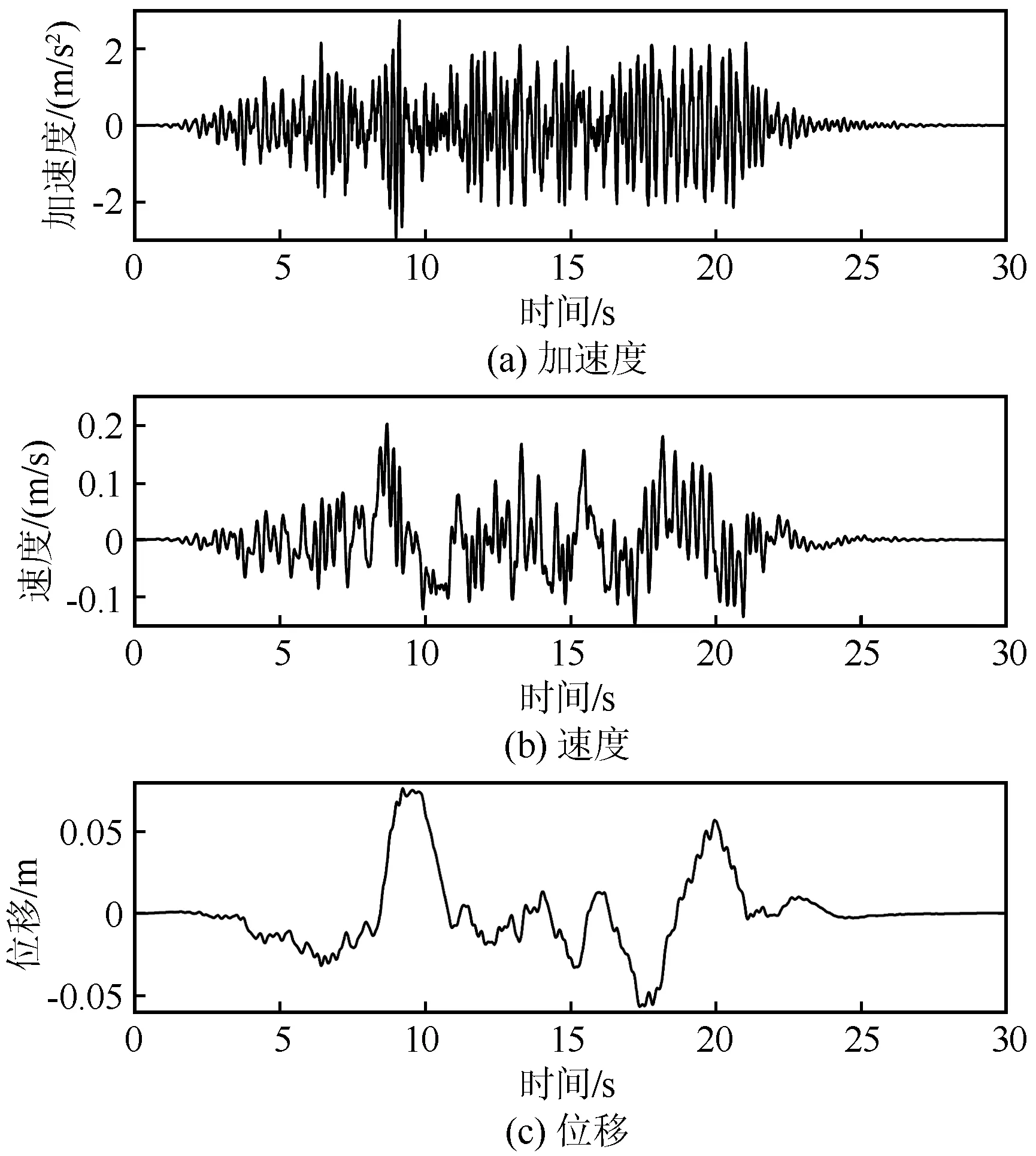
圖5 基線歸零的人工地震波時程Fig.5 Time history of artificial seismic wave with zero baseline

4 結論

在傳統頻域法的基礎上提出一種人工地震波反應譜直接擬合方法,采用多組設計反應譜驗證了所提方法的匹配精度。本方法內蘊基線歸零條件,將匹配目標反應譜問題轉化為以幅值譜為目標的非線性方程進行快速迭代求解,具有編程友好、收斂精度高的特點。總結本文可得如下結論:

(1) 所提方法以求導代替積分為總體思路,在快速擬合算法中內蘊基線歸零條件,能夠同時給出滿足歸零條件的位移、速度和加速度時程,避免了傳統方法加速度積分過程中的基線漂移問題。

(2) 以單自由度系統諧波響應解析解為依據,將匹配目標譜的人工地震波擬合問題轉化為以待求幅值譜為變量的非線性方程組。采用高效的非線性方程求解器進行迭代,具有收斂速度快,低頻、高頻段擬合精度高的優勢。

(3) 考慮了相位譜進行綜合迭代,匹配效率和匹配精度進一步提高。所提算法編程難度低,且不必構造復雜的迭代格式。

(4) 核電樓層譜呈現宏觀“峰多谷深”、局部“轉折”細節較多的特點,對高精度人工波擬合提出了更高的挑戰。因此,所提算法對復雜樓層譜的擬合能力需要進一步改進和優化,同時也需要給出篩選判據,有效排除理論上難以匹配目標反應譜的人工地震波,提高整體擬合效率。