解答三角函數問題的常見數學思想應用分析

張守城 唐玲

【摘 ?要】 ?三角函數是對高中數學函數知識與三角形知識的重要延伸，同時也是高中數學中的重難點知識之一.與三角函數有關的問題，其命題形式靈活多變且具有一定難度，結合常見的數學思想有助于問題的解答.本文主要介紹兩種常見數學思想求解高中數學三角函數問題，以此幫助學生快速找到解題關鍵，從而提高解答三角函數問題的效率.

【關鍵詞】 ?高中數學；三角函數；數形結合

1 ?數形結合思想

數形結合思想是解答三角函數問題的基本且重要的思路，運用的關鍵在于根據三角函數解析式得到相關圖象，再從具體圖象出發得到滿足要求的關系等式，從而對問題做出完整解答.數形結合思想的運用，在三角函數解析式問題、具體函數值問題都有明顯體現.運用數形結合思想解題，一般解題步驟可表現為：①結合已知條件畫出具體三角函數圖象，②分析圖象特點，結合具體值得到三角函數的周期大小、拐點坐標，③將圖象的坐標、值的大小代入相關等式中，得到問題所求.

例已知函數的部分圖象如圖所示，試求函數的解析式.

圖

剖析 該題主要對三角函數的圖象進行具體分析，從圖象可得知拐點坐標、與軸的交點坐標，將其代入三角函數解析式中，可求出的大小，即可得到三角函數的具體解析式.

解析 ?由圖象可知，

且，

得.

又因為，

所以，

將最高點代入上式，

可知，

故，

因為，所以，

故函數解析式為.

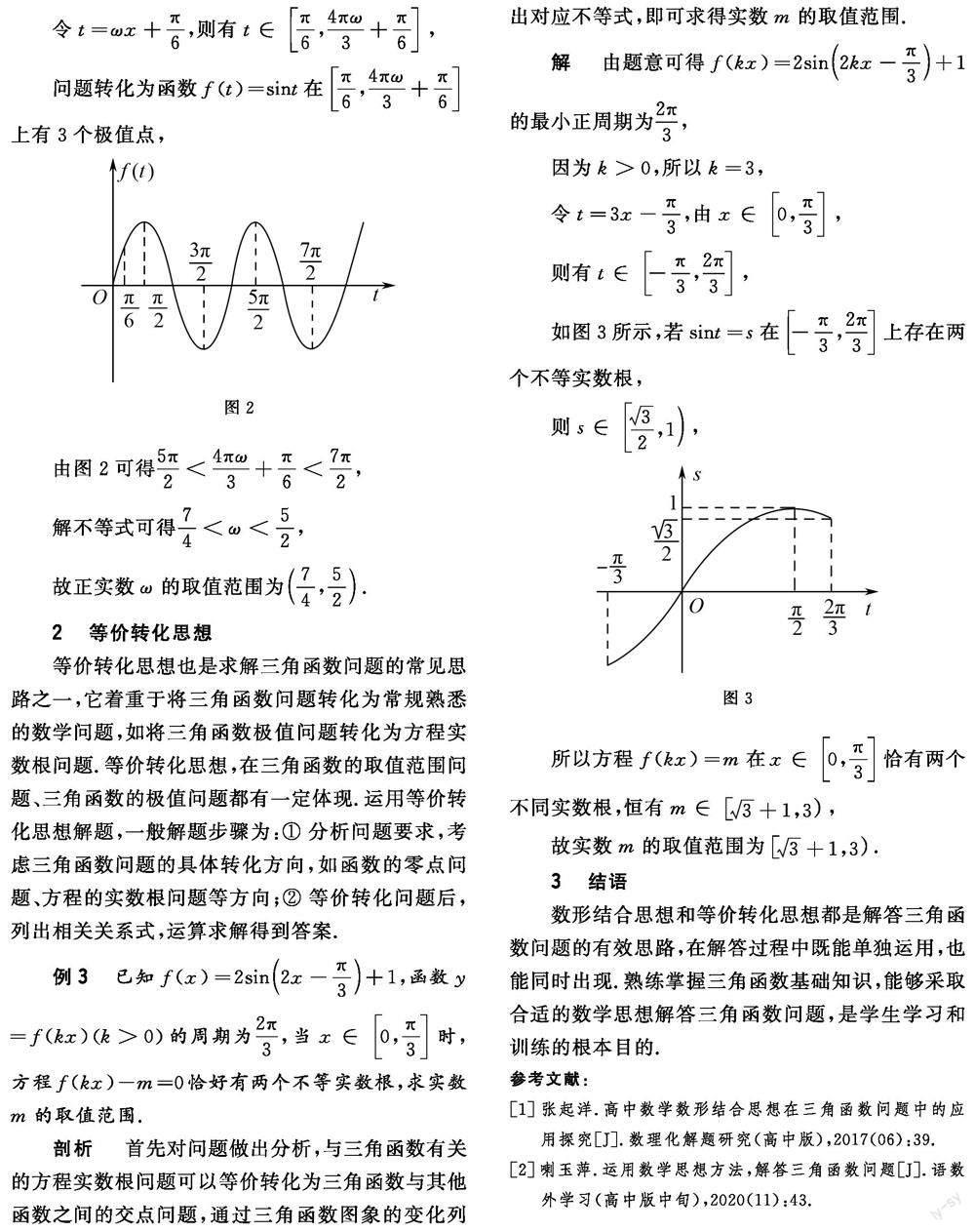
例已知，，在上恰有個極值點，則正實數的取值范圍為_____.

剖析首先根據問題要求得到三角函數解析式，在規定范圍內求解三角函數的極值點個數，可以結合三角函數具體圖象進行解答，即在規定區間內有三個拐點，可根據圖象列出不等式，運算求解即可得知實數的取值范圍.

解析由題意可得，

令，則有，

問題轉化為函數在上有個極值點，

圖2

由圖象可得，，

解不等式可得，

故正實數的取值范圍為.

2 ?等價轉化思想

等價轉化思想也是求解三角函數問題的常見思路之一，著重于將三角函數問題轉化為常規熟悉的數學問題，如將三角函數極值問題轉化為方程實數根問題.等價轉化思想，在三角函數的取值范圍問題、三角函數的極值問題都有一定體現.運用等價轉化思想解題，一般解題步驟為：①分析問題要求，考慮三角函數問題的具體轉化方向，如函數的零點問題、方程的實數根問題等方向，②等價轉化問題后，列出相關關系式，運算求解得到答案.

例已知，函數的周期為，當時，方程恰好有2個不等實數根，求實數的取值范圍.

剖析 首先對問題做出分析，與三角函數有關的方程實數根問題可以等價轉化為三角函數與其他函數之間的交點問題，通過三角函數圖象的變化列出對應不等式，即可求得實數的取值范圍.

解析 ?由題意可得的最小正周期為，

因為，所以，

令，由，

則有，

如圖所示，若在上存在兩個不同解，

則，

圖

所以方程在恰有2個不同實數根，恒有，

故實數m的取值范圍為.

3 ?結語

數形結合思想和等價轉化思想都是解答三角函數問題的有效思路，在解答過程中存在交叉現象，即兩種數學思想既能單獨運用在三角函數問題上，也能同時出現在三角函數問題解答過程中.熟練掌握三角函數基礎知識，采取合適的數學思想解答三角函數問題，也就達到同學們學習和訓練的根本目的.

參考文獻：

• 張起洋.高中數學數形結合思想在三角函數問題中的應用探究[J].數理化解題研究（高中版），2017（06）：39.

[2]喇玉萍.運用數學思想方法，解答三角函數問題[J].語數外學習（高中版中旬），2020（11）：43.