求解弱雙四元數(shù)矩陣方程r-循環(huán)解的新方法

劉志紅, 李 瑩, 樊學玲, 襲沂蒙

(聊城大學數(shù)學科學學院, 山東 聊城 252000)

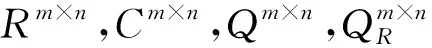
矩陣方程是數(shù)值代數(shù)的重要研究領域之一, 其中關于矩陣方程

AX+XB=D

(1)

的研究, 已經(jīng)有一定的進展. 如尤興華等研究了復數(shù)域上矩陣方程(1)的簡潔解及其應用[1], Zhang等研究了實數(shù)域上矩陣方程(1)對稱解及反對稱解的松弛梯度迭代算法[2], Wang等研究了復數(shù)域上矩陣方程(1)的正定和反Hermitian分裂迭代法[3], 有些學者還研究了不同四元數(shù)集合上的矩陣方程(1), 如Tian等研究了弱雙四元數(shù)集合上矩陣方程(1)的反Hermitian問題[4], 而Li等研究了分裂四元數(shù)集合上矩陣方程(1)的反Hermitian問題[5].

四元數(shù)最早是由Hamilton提出的, 一個四元數(shù)集合可以表示為

Q={q|q=q1+q2i+q3j+q4k,q1,q2,q3,q4∈R,
i2=j2=k2=-1,ij=-ji=k}．

由四元數(shù)的乘法規(guī)則發(fā)現(xiàn), 四元數(shù)可以看作是實數(shù)域上的四維非交換代數(shù).四元數(shù)在許多領域具有廣泛的應用, 如姿態(tài)控制[6-7]、機器人[8-9]、數(shù)據(jù)處理[10]等, 但是四元數(shù)乘法不滿足交換性, 這在一定程度上限制了它的應用范圍.針對四元數(shù)乘法的不可交換性, 弱雙四元數(shù)應運而生, 且已被應用于諸多領域, 如基于弱雙四元數(shù)的矩陣方程的求解[11-13], 基于弱雙四元數(shù)的彩色圖像處理[14], 基于弱雙四元數(shù)模型的航天器升軌姿態(tài)控制[15], 基于弱雙四元數(shù)的彩色紋理分類[16]等.

特殊矩陣的理論與實際應用受到廣泛關注.美國學者Muir于1958年提出循環(huán)矩陣的概念,如今在計算數(shù)學、應用數(shù)學、現(xiàn)代科技工程等領域具有廣泛的應用[17-20].作為循環(huán)矩陣的推廣,r-循環(huán)矩陣也受到許多學者的廣泛關注, 如Lyes研究了r-循環(huán)矩陣的范數(shù)及超Lucas數(shù)新推廣的一些組合性質(zhì)[21], Ramazan研究了(k,h)-Fibonacci和(k,h)-Lucas數(shù)的r-循環(huán)矩陣的譜范數(shù)[22]．

為了去除具有特殊結構的矩陣中的重復元素, Zhang提出一種H-表示方法, 即給出一種提取矩陣獨立元素的系統(tǒng)性的方法[23].目前,H-表示在系統(tǒng)與控制理論等方面有初步應用, 如Wang利用H-表示方法研究了具有多噪聲的馬爾科夫跳變隨機系統(tǒng)的精確能觀性[24], Zhao利用H-表示方法研究了非線性離散隨機時滯系統(tǒng)的矩穩(wěn)定性[25].本文利用弱雙四元數(shù)的實表示方法與特殊矩陣的H-表示方法研究弱雙四元數(shù)矩陣方程(1)的r-循環(huán)解和對稱r-循環(huán)解.

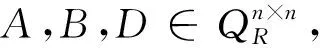
LC={X|X∈Cr(x1,x2,…,xn),

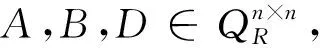
LSC={X|X∈SCr(x1,x2,…,xn),

1 預備知識

定義1[26]若q∈QR, 則q可唯一的表示成q=q1+q2i+q3j+q4k, 其中q1,q2,q3,q4∈R,i,j,k滿足

i2=k2=-1,j2=1,ij=ji=k,jk=kj=i,ki=ik=-j．

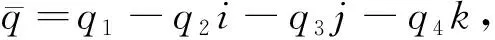
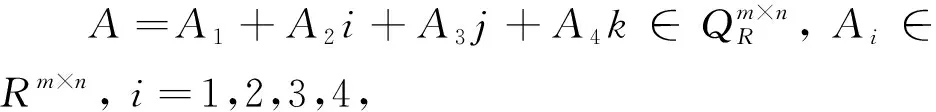
其實表示的第一列塊定義為

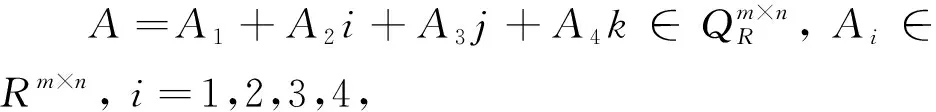
定義4[29]設A為m×n維的矩陣,則其列排式定義為

vec(A)=[a11,…,am1,a12,…,am2,…,a1n,…,amn]Τ．

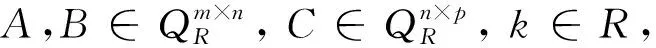
1)A=B?AR=BR;

2) (A+B)R=AR+BR, (kA)R=kAR, (AC)R=ARCR;

引理2[31]設A∈Rm×n,b∈Rm, 線性方程組Ax=b的最小二乘解可以表示為

x=A?b+(I-A?A)y,

其中,y∈Rn是任意的.矩陣方程Ax=b的極小范數(shù)最小二乘解為A?b．

引理3[31]設A∈Rm×n,b∈Rm, 線性方程組Ax=b有解x∈Rn當且僅當AA?b=b, 此時, 它的通解表達式為

x=A?b+(I-A?A)y,

其中,y∈Rn是任意的.矩陣方程Ax=b的極小范數(shù)解為A?b．

對于實矩陣A∈Rm×n,B∈Rn×p,C∈Rp×q,vec算子有性質(zhì)vec(ABC)=(CΤ?A)vec(B), 可以發(fā)現(xiàn)該性質(zhì)對弱雙四元數(shù)依然成立．

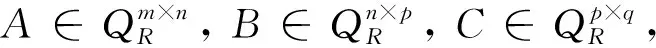
vec(ABC)=(CΤ?A)vec(B).

(2)

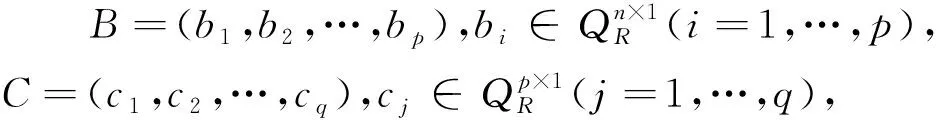
而

ABci=c1iAb1+c2iAb2+…+cpiAbp=
(c1iA,c2iA,…,cpiA)vec(B)．

故

(CΤ?A)vec(B)．

2 r-循環(huán)矩陣及對稱r-循環(huán)矩陣的H-表示

本節(jié)將對特殊矩陣, 即r-循環(huán)矩陣及對稱r-循環(huán)矩陣的H-表示進行介紹．

定義5[32]形如

的矩陣稱為r-循環(huán)矩陣.當r=1時,A為通常的循環(huán)矩陣; 當r=0時,A為上三角Toeplitz矩陣;當r=-1時,A為通常的反循環(huán)矩陣．

定義6[32]形如

的矩陣稱為對稱r-循環(huán)矩陣.當r=1時,A為通常的對稱循環(huán)矩陣;當r=0時,A為上三角Hankel矩陣;當r=-1時,A為通常的對稱反循環(huán)矩陣.

定義7[23]考慮一個m維復矩陣子空間Μ?Cn×n, 對每個矩陣X=(xij)n×n∈Μ, 總存在一個映射ψ：X∈Μvec(X).如果dim(Μ)=m,e1,e2,…,em組成Μ的一組基,m≤n2, 那么存在x1,x2,…,xm∈C, 使得定義H=[vec(e1),vec(e2),…,vec(em)], 那么對每個X∈Μ, 都可以用一個m×1維向量將ψ(X)=vec(X)表示成

(3)

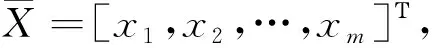
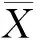
例1設Μ=Cr(a1,a2,a3),X=(xij)3×3∈Μ, dim(Μ)=3．

選擇Μ的一組基底

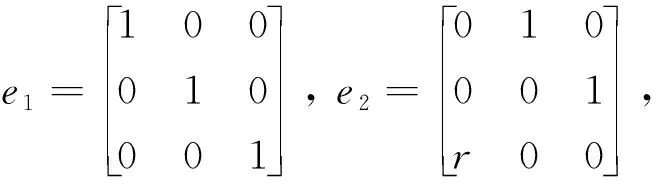
易得

ψ(X)=vec(X)=[a1ra3ra2a2a1

其中,

例2設Μ=SCr(a1,a2,a3),X=(xij)3×3∈Μ, dim(Μ)=3．

選擇Μ的一組基底

易得

ψ(X)=vec(X)=[a1a2a3a2a3ra1

其中,

本文將對X∈Μ=Cr(a1,a2,…,an)以及X∈Μ=SCr(a1,a2,…,an)做H-表示, 先選取n階r-循環(huán)矩陣以及n階對稱r-循環(huán)矩陣的標準基底．

定理2對r-循環(huán)矩陣子空間Μ=Cr(a1,a2,…,an), 選取一組標準基底

{E1j|1≤j≤n},

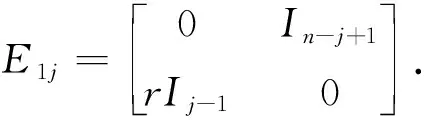
(4)

同樣的, 對于對稱r-循環(huán)矩陣子空間Μ=SCr(a1,a2,…,an), 選取一組標準基底

{F1j|1≤j≤n},

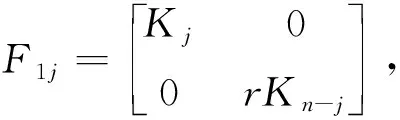
(5)

3 問題1及問題2的解

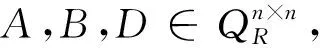
SC={X=X1+X2i+X3j+X4k|XV=

(6)

并且, 極小范數(shù)最小二乘r-循環(huán)解XC滿足

(7)

證明對X∈Cr(x1,x2,…,xn), 由引理1可以得到

由于X∈Cr(a1,a2,…,an), 根據(jù)定理3可得

定義H1=diag(HC,HC,HC,HC),L1=((In?A)R+(BΤ?In)R)H1, 那么

因此,

(8)

方程(8)的兩邊乘以矩陣H1可得到方程(7).同時, 可以得到式(6)．

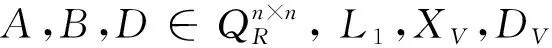
(9)

此外, 如果(9)成立,則弱雙四元數(shù)矩陣方程(1)的r-循環(huán)解集可表示為

SC={X=X1+X2i+X3j+X4k|XV=

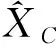
(10)

證明弱雙四元數(shù)矩陣方程(1)有r-循環(huán)解當且僅當

由定理3及MP逆的性質(zhì)得

因此, 對X∈Cr(x1,x2,…,xn), 可以得到

如果弱雙四元數(shù)矩陣方程(1)相容, 那么該方程解X∈Cr(x1,x2,…,xn)滿足

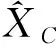
同樣, 可將上述方程的兩邊乘以矩陣L1得到SC, 并可得到極小范數(shù)r-循環(huán)解(10)．

類似的, 可以得到問題2的極小范數(shù)最小二乘對稱r-循環(huán)解和極小范數(shù)對稱r-循環(huán)解．

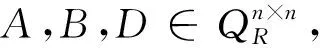
SSC={X=X1+X2i+X3j+X4k|XV=

(11)

并且, 極小范數(shù)最小二乘對稱r-循環(huán)解XSC滿足

(12)

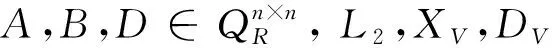
(13)

此外, 如果(13)成立,則弱雙四元數(shù)矩陣方程(1)的對稱r-循環(huán)解集可表示為

SSC={X=X1+X2i+X3j+X4k|XV=

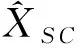
(14)

4 數(shù)值算例

算法1(問題1)

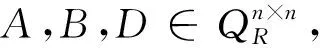
步驟2輸入HC, 輸出H1,L1.

步驟3根據(jù)公式(7), 輸出弱雙四元數(shù)矩陣方程(1)的極小范數(shù)最小二乘r-循環(huán)解XC.

算法2(問題2)

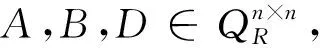
步驟2輸入HSC, 輸出H2,L2.

步驟3根據(jù)公式(12), 輸出弱雙四元數(shù)矩陣方程(1)的極小范數(shù)最小二乘對稱r-循環(huán)解XSC.

算例令n=2:30, 在Matlab中隨機生成n階弱雙四元數(shù)矩陣A,B, 取

圖1 問題1的誤差Fig.1 Errors in problem 1

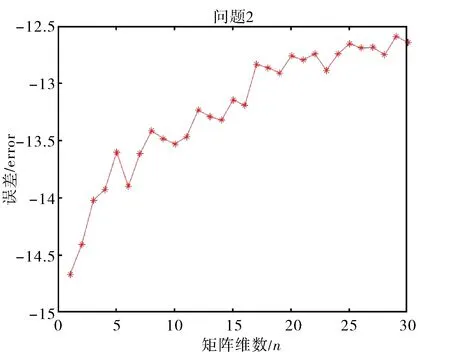
圖2 問題2的誤差Fig.2 Errors in problem 2

5 應用

山地果園荔枝的采摘方式通常為人工采摘, 但隨著科技的發(fā)展, 越來越多人選擇利用智能機器人采摘.本節(jié)研究矩陣方程AX+XB=D在荔枝采摘機器人手眼標定方法中的應用.機器人的手眼標定涉及標定板、相機系統(tǒng)、機器人、機器人的機械臂 4 個對象的空間位置關系[33].當相機對標定板進行第i次觀測時,考慮到實際操作的誤差, 實際情況下2次觀測的數(shù)據(jù)所得到的手眼方程形式為

AX+XB=D．

考慮解X為r-循環(huán)型矩陣的情況.選取以下參數(shù)矩陣

利用本文方法,求得

由于

L1=((I3?A)R+(BΤ?I3)R)diag(H,H,

H,H),

因此弱雙四元數(shù)矩陣方程(1)的r-循環(huán)解為

6 小結

本文根據(jù)弱雙四元數(shù)性質(zhì), 借助vec算子及四元數(shù)的實表示方法對弱雙四元數(shù)方程AX+XB=D進行轉化, 然后利用特殊矩陣的H-表示方法提取矩陣的獨立元素, 得到求解該方程的一種新方法. 該方法可以減少參與運算的元素個數(shù), 減少運算的復雜程度,可應用于荔枝采摘機器人的手眼標定．