面向艦艇編隊的無人機集群物資補給規(guī)劃研究
郭文強, 李子展, 候勇嚴, 薛博豐
(1.陜西科技大學 電子信息與人工智能學院, 陜西 西安 710021; 2.陜西科技大學 電氣與控制工程學院, 陜西 西安 710021)
0 引言
艦艇編隊作為海上軍事力量的直接體現(xiàn),為其提供必要的物資保障對于增強艦艇編隊的作戰(zhàn)能力、擴大艦艇編隊的作戰(zhàn)半徑來說是不可或缺的.如何合理規(guī)劃物資補給路徑,提高物資補給效率,對于提升艦艇編隊作戰(zhàn)能力具有重大意義[1].無人機基于其自身的多功能、高移動、易部署和低成本等優(yōu)勢,被用作空天地海一體化網(wǎng)絡架構中空域輔助平臺,在越來越多的場景中承擔重要角色[2].
驅逐艦、護衛(wèi)艦、航母等構成的艦艇編隊中的補給艦,其特點是噸位較大(以美軍供應級支援艦為例,該級艦滿載排水量近5萬噸)、專業(yè)艙室多、所帶物資齊全、補給設施配套,既有淡水、糧食、蔬菜、水果等生活物資,也有柴油、航空燃油、彈藥等作戰(zhàn)物資,還有各種用于應急搶修的備品、備件.它能在通過“吞吐”大量物資,對各類艦艇進行補給.
規(guī)模較大的艦艇編隊遠航,需要的補給艦往往不止一艘.目前針對艦艇編隊的物資補給規(guī)劃研究主要利用“補給艦”對艦艇進行補給,同時構建約束規(guī)劃模型并對其進行求解得出最優(yōu)補給方案.文獻[1]構建了以補給艦艇數(shù)量最少和補給時間最短為目標的多目標約束規(guī)劃模型,并利用改進后的遺傳算法對其進行求解;文獻[3]構建了以最小化補給成本為目標,以補給水平為約束的分段式補給模型;文獻[4]建立了以最大化作戰(zhàn)效能為目標的補給規(guī)劃模型并使用模擬退火算法對其進行求解.然而,在浪、風、涌等復雜海況下,艦艇操作難度大,稍有不慎就會出現(xiàn)撞船事故[5].
相較補給艦,無人機作為一種補給裝置,其智能性與安全性水平不斷快速提升,裝置結構易于標準化,批量化設計、生產(chǎn)使其造價較低,可減少補給設備種類、降低補給成本、方便操作與維修的同時,另外無需要飛行人員,所以最大可能地保障了人的生命安全.上述突出的優(yōu)點可使無人機保障系統(tǒng)達到最佳補給效果.
但現(xiàn)有文獻中利用無人機集群對艦艇編隊進行物資補給的研究較少,使用無人機進行物資補給具有在特殊環(huán)境下可以實現(xiàn)人員零傷亡、自身極強的隱蔽性等優(yōu)勢.本文探討了利用無人機集群針對艦艇編隊進行物資補給規(guī)劃的問題,使用非線性自適應遺傳算法(Nonlinear Adaptive Genetic Algorithm ,NLAGA)對構建的多約束條件下的物資補給規(guī)劃模型進行求解,得到所需的無人機群數(shù)量、最優(yōu)補給路徑以及最小時間成本.
1 面向艦艇編隊的物資補給規(guī)劃模型
1.1 問題描述
假設現(xiàn)有一個由M架無人機組成的無人機集群,計劃利用其對某艦艇編隊進行彈藥補給(該艦艇編隊由N艘艦艇組成).規(guī)定所有無人機均從補給中心起飛,并且每架無人機的補給能力有限,無人機的補給路線長度滿足各自通航距離.同時,由于通行時刻不同導致同一路徑上無人機的行駛速度也不同.無人機從物資補給中心出發(fā),在規(guī)定時間窗內(nèi)對艦艇編隊進行補給,完成對所有艦艇的補給后返回物資補給中心.每個艦艇都有設定的服務時間窗(僅在此時間范圍內(nèi)能進行補給作業(yè))和不同的物資需求量,目標是確定無人機群所需無人機數(shù)量,并確定補給路線,用最少的時間完成所有補給任務,實現(xiàn)補給成本最優(yōu)的目標.
1.2 無人機飛行時間成本
無人機在執(zhí)行任務時的飛行時間與無人機的飛行速度以及艦艇之間的距離相關.飛行時間Tf為:
(1)
1.3 補給作業(yè)時間成本
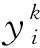
到達艦艇后的物資準備時間Tp為:
(2)
式(2)中:pi為艦艇i的物資準備時間.
補給花費時間Ts為:
(3)
式(3)中:si為無人機在艦艇i的物資補給作業(yè)所花費的時間.
綜上,無人機的總補給作業(yè)時間成本Tw為:
Tw=Tf+Tp+Ts
(4)
1.4 時間懲罰成本

(5)
令M2表示延誤到達的懲罰系數(shù),則延誤到達的時間懲罰成本為:
(6)
因此考慮無人機允許補給作業(yè)時間窗的時間懲罰成本Tpc為:
Tpc=Cae+Cal
(7)
1.5 面向艦艇編隊的無人機物資補給規(guī)劃模型
考慮將無人機的作業(yè)時間以及時間窗約束而產(chǎn)生的懲罰成本,同時將無人機作業(yè)時間窗、安全返航、物資需求量與無人機總最大載重量等約束條件,本文構建的面向艦艇編隊的無人機物資補給規(guī)劃模型如下:
(8)

2 求解補給規(guī)劃問題的NLAGA算法
對于每架無人機來說,補給任務可視為帶時間窗限制的車輛路徑規(guī)劃問題,此類問題已被證明是NP(non-deterministic polynomial,非確定性多項式)[8]難題.啟發(fā)式算法是目前解決NP難題的有效方法之一[9].在這些啟發(fā)式算法中,遺傳算法(Genetic Algorithm ,GA)和改進的遺傳算法因其快速收斂而被廣泛采用,故本文采用遺傳算法對物資補給規(guī)劃路徑進行染色體(基因)編碼,并對物資補給規(guī)劃模型進行求解.
遺傳算法本質上是一種通過模擬自然進化來搜尋最優(yōu)解的方法,其中交叉、變異概率(Pc、Pm)對算法的性能起著決定性的作用.傳統(tǒng)GA中交叉、變異概率為定值,在進化后期容易對最優(yōu)解造成破壞,因此可能會導致早熟收斂現(xiàn)象的產(chǎn)生.文獻[10]提出了一種改進的自適應遺傳算法(Improved Adaptive Genetic Algorithm ,IAGA),其中交叉、變異概率計算方法如下:
(14)
(15)
式(14)、(15)中:fmax表示種群中染色體適應度最大值,f代表交叉操作染色體中的適應度值,fa代表種群染色體適應度均值,f′代表待變異操作染色體的適應度值,其它參數(shù)常取Pc1=0.9、Pc2=0.6、Pm1=0.1、Pm2=0.01.
IAGA可以通過自適應調節(jié)概率來保留最優(yōu)解,在一定范圍可緩解GA早熟收斂現(xiàn)象.但在進化中段,種群中染色體的交叉、變異概率普遍很低,從而可能導致交叉、變異操作失效,出現(xiàn)進化停滯的現(xiàn)象.為了減少此類風險,本文對IAGA進行了進一步的改進.
2.1 非線性概率函數(shù)
本文引入Sigmoid函數(shù)[11]設計了一類非線性的交叉概率和變異概率計算函數(shù),分別表達如下:
(16)
(17)
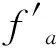
(18)
2.2 艦艇編隊的無人機物資補給規(guī)劃算法-NLAGA
基于非線性概率函數(shù)設計的補給規(guī)劃模型的NLAGA算法步驟如下:
第1步:確定各艦艇物資需求量Qi(i=1,2,…,N)、艦艇坐標、艦艇補給時間窗、補給作業(yè)時間,懲罰系數(shù)M1、M2,輸入每架無人機的最大補給量、速度范圍,以及進化算法操作系數(shù)A、B、C,最大迭代次數(shù)MaxGen和尋優(yōu)收斂誤差ε.
第2步:根據(jù)公式(8)至(13)描述的規(guī)劃模型,利用文獻[12]的方法將其表示為2N條補給規(guī)劃的初始染色體.
第3步:令迭代次數(shù)iter=1.
第4步:根據(jù)公式(8)計算每條染色體的適應度函數(shù),并選擇目標函數(shù)最小的Ztemp.
第5步:利用式(14)計算交叉概率并執(zhí)行交叉操作[13].
第6步:利用式(15)計算變異概率并執(zhí)行變異操作[12],形成新的染色體種群.
第7步:根據(jù)公式(8)計算每條染色體的適應度Znew.
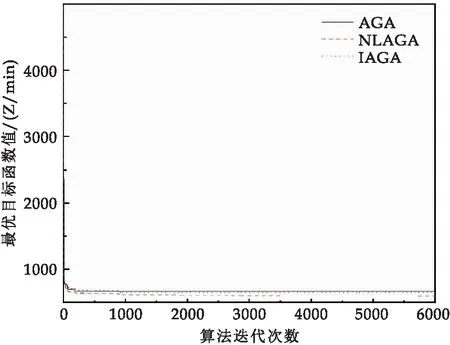
第8步:若Znew 第9步:若Znew-Z*<ε,則跳轉至第11步;否則iter=iter+1,執(zhí)行第10步. 第10步:若iter=MaxGen,進入第11步;否則返回執(zhí)行第4步,繼續(xù)進化尋優(yōu). 為了驗證NLAGA算法在求解補給規(guī)劃問題中的優(yōu)越性的性能,本文將無人機補給規(guī)劃問題抽象為帶時間窗約束的車輛路徑問題(VRPTW)并使用經(jīng)典的Solomen數(shù)據(jù)集[14]中r101的算例進行測試.將NLAGA算法與文獻[13]中所提出的AGA算法以及IAGA算法進行對比. 61個待補給點位置已知,所需物資量均為Qi=150 kg(i=1,2,…,61),時間懲罰系數(shù)M1=10、M2=100;無人機速度vmin=0 km/min,vmax=0.8 km/min,單架最大補給量50 kg;最大迭代次數(shù):MAXGEN=6 000;步長λ=200;交叉、變異系數(shù):A=4、B=6、C=0.55;為了達到相同的迭代次數(shù),實驗中將收斂誤差ε設為0.其它參數(shù)選擇參考同文獻[13]. 仿真平臺為Matlab版本R2016a,所有測試都在配置了2.3 GHz Intel Core i10處理器和8.0 GB內(nèi)存、Windows 10系統(tǒng)的計算機上進行. 為了減少隨機性對實驗結果的影響,實驗中將不同求解方法獨立運行15輪,記錄其均值.求解后該補給任務均需15架無人機參與補給任務,得到目標函數(shù)值變化曲線如圖1所示. 圖1 目標函數(shù)值變化曲線 不同算法求解的最優(yōu)值、均值以及方差,分別如表1、表2、表3所示. 表1 不同算法求解的目標函數(shù)最優(yōu)值 表2 不同算法求解的目標函數(shù)的均值 表3 不同算法求解的目標函數(shù)的方差 由圖1可看出,在本實驗中,不同算法求解在迭代至3 500輪時尋優(yōu)過程趨于穩(wěn)定.在相同迭代次數(shù)時,由表1至表3可知,利用NLAGA得到的最優(yōu)解及其均值、方差均優(yōu)于AGA和IAGA方法. 分析可知:在計算機模擬隨機取值條件下,NLAGA中的非線性概率函數(shù)可以在進化中段,通過本文設計的非線性函數(shù)的拉伸,擴大了概率的取值范圍,有利于采樣到更豐富的交叉和變異概率值,提高了算法在求解空間的尋優(yōu)探索能力,有利于保留最優(yōu)解,有效避免了進化停滯的現(xiàn)象. 3.2 面向艦艇編隊的無人機物資補給規(guī)劃實驗與分析 本實驗針對某艦艇編隊的補給規(guī)劃任務進行了求解.假設該艦艇編隊的待補給艦艇數(shù)量為15艘.補給中心的相對坐標為(660,750)km,現(xiàn)利用相同性能的無人機執(zhí)行補給規(guī)劃任務,飛行速度為vmin=0 km/min,vmax=0.8 km/min,此外假設每艘艦艇所需的物資準備時間pi均為5 min(i=1,2,…,N),其他參數(shù)如表4所示.利用本文提出的NLAGA算法求解該問題,將收斂誤差ε設為0.001,其他參數(shù)取值同3.1. 表4 補給任務相關參數(shù) 利用本文提出的NLAGA算法解算出完成該補給規(guī)劃任務需要5架無人機,完成補給規(guī)劃任務最短耗時為291.309 1 min. 完成本次補給規(guī)劃任務的無人機群最優(yōu)補給路徑、目標函數(shù)值及規(guī)劃耗時的變化分別如圖2和圖3所示. 圖2 無人機補給路徑示意圖 圖3 目標函數(shù)值及規(guī)劃耗時變化曲線 本文針對無人機集群對艦艇編隊的物資補給規(guī)劃問題,以艦艇補給時間窗、無人機最大載重量等為約束條件,構建了無人機集群補給規(guī)劃模型.在自適應遺傳算法的基礎上,設計了非線性的交叉概率函數(shù)和變異概率函數(shù),并提出了一種無人機物資補給規(guī)劃算法NLAGA.實驗結果表明:NLAGA法的性能要優(yōu)于AGA和IAGA方法,可有效地解決無人機集群對艦艇編隊的物資補給規(guī)劃問題,為實現(xiàn)艦艇編隊的物資補給提供科學的決策支持.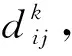
3 實驗結果與分析
3.1 算法性能測試




4 結論

