基于近鄰搜索空間提取的LOF算法

王若雨,趙千川,楊 文,2

(1.清華大學 自動化系智能與網絡化系統研究中心,北京 100084;2.航天發射場可靠性重點實驗室,海口 570100)

異常檢測是數據挖掘領域一項非常重要的技術,廣泛應用于金融、網絡、保險、股票等多個領域[1]。基于相對密度的局部異常因子(local outlier factor,LOF)[2]算法是目前應用最廣泛且最有效的無參數異常檢測算法之一,尤其是對于呈偏態分布的數據集。有鑒于此,相關文獻[3-12]開展了大量基于LOF的研究,但對于LOF的局限性,人們依然沒有找到較好的改進方法,這使得該算法無法拓展到數據規模更大以及檢測精度需求更高的應用場景中。第一,其時間復雜度較高,由于LOF要分別對n個樣本點進行k近鄰搜索,因此使用線性掃描方法的時間復雜度為O(n2)。第二,其空間復雜度較高,由于LOF算法需要存儲每對數據點的距離信息,因此其空間復雜度也為O(n2)。這使得該算法無法應用于數據流處理中,因為隨著數據源源不斷的到達,LOF所需內存將持續增大,直到無法處理[8]。第三,LOF對交叉異常以及低密度簇周圍異常點識別不敏感。在真實場景中,正異常點通常不是涇渭分明而是交錯在一起的,LOF對這種緊鄰正常數據簇且與其存在一定交叉的異常點的識別不敏感,最差情況下LOF將退化為隨機檢測器。同時在真實數據集中,正常數據的分布不會只集中在一個區域,而是分布在多個密度不同的簇中,雖然與多數算法相比,LOF可以較為有效地檢測出這種存在于非均勻密度數據中的異常點,但其仍存在局限性,即相比于高密度簇,低密度簇正常點周圍的異常點更容易被LOF算法忽略。

1 理論基礎

LOF算法通過計算局部離群因子來衡量每個數據點的異常程度,數據點a局部離群因子的計算以及分析需要以下定義以及定理,其中定理1的具體證明過程參見文獻[2]。

定義1點a與其第k鄰域點之間的歐氏距離為dk(a)。

定義2點o到點a的可達距離為

dreach,k(a,o)=max{dk(o),d(a,o)}

(1)

式中d(a,o)為點a和點o之間的歐氏距離。

定義3點a的局部可達密度為

(2)

式中Nk(a)為a點k近鄰數據點的集合。

定義4點a的局部離群因子為

(3)

定義5點a第k鄰域中一點到點a可達距離的最小值以及最大值為

Fmin(a)=min{dreach,k(a,b)|b∈Nk(a)}

(4)

Fmax(a)=max{dreach,k(a,b)|b∈Nk(a)}

(5)

定義6點a第k鄰域中一點b的第k鄰域中一點到點b可達距離的最小值以及最大值為

Smin(a)=min{dreach,k(b,o)|b∈Nk(a)且o∈Nk(b)}

(6)

Smax(a)=max{dreach,k(b,o)|b∈Nk(a)且o∈Nk(b)}

(7)

定理1假設a為數據集D中的一個樣本點,并且1≤k≤|D|,則點a局部離群因子的范圍為

(8)

2 iDELOF算法

iDELOF異常檢測算法,將iKSSE前置于LOF算法,高效剪切掉大量無用及干擾數據,獲得更加精準的搜索空間,極大提升LOF異常檢測算法的效率及效果。算法分為近鄰搜索空間提取(iKSSE)、異常分數計算(anomaly score calculation,ASC)兩個階段,每個階段又分為兩步。

2.1 第一階段iKSSE

iKSSE分為構造數據提取森林、提取近鄰搜索空間兩步。

第一步,構造數據提取森林。利用孤立森林[13]提出的隔離思想對數據隨機選擇屬性、隨機設定閾值分隔為左右葉子節點,不斷迭代重復,直到葉子節點中只有一個樣本點或所有樣本點取值相同,或者提取樹到達最大設定閾值l。與IF算法建立的隔離樹一樣,提取樹也為二叉樹,其中每個節點又分為擁有兩個葉子節點的內部節點以及沒有葉子節點的外部節點兩種類型;與隔離樹的區別在于,提取樹中每個外部節點的存儲內容不再是數據點的數量,而是所有被分割到此節點的數據點以及數據點在樹中對應的深度,即數據點被分割的次數。按上述方法,在多個隨機抽取的樣本子集上建立t棵提取樹,組合成為數據提取森林。構建數據提取森林的具體細節見算法1、2。

算法1iDETree(X,c,l)

Input:X-input data,c-current tree depth,l-depth limit

Output:aniDETree

1:ifc≥lor|X|≤1 then

2: returnexNode{data←X,depth←c}

3:else

4: letAbe a list of attributes inX

5: randomly choose an attributea∈A

6: randomly choose a divide pointbfromminandmaxvalue of attributeainX

7:Xl←filter(X,a≤b)

8:Xr←filter(X,a>b)

10:end if

算法2iDEForest(X,t,φ)

Input:X-input data,t-number of trees,φ-subsample size

Output:a group ofiDETrees

1:InitializeiDEForest

2:set depth limitl=ceiling(log2φ)

3:fori=1∶tdo

6:end for

7:returniDEForest

第二步,提取近鄰搜索空間。遍歷提取森林中的所有外部節點,取出每棵樹中深度位于設定的深度閾值Ct以下的外部節點中的所有樣本,即位于數據集全局較中心的數據,并且將在所有樹中提取到的數據合并得到候選數據。最后根據設定的次數閾值N,在候選數據中篩選出提取次數超過N的所有數據,作為第二階段近鄰數據的搜索空間。從構建好的森林中提取近鄰數據搜索空間的具體細節見算法3、4。

算法3DataExtraction(T,Ct)

Input:T-an iDETree,Ct-depth threshold

Output:candidate_datafrom an iDETree

1:ifTis an external node

2: ifT.depth>Ctthen

3: returnT.data

4: end if

5:else

6: returncombine(DataExtraction(T.left,Ct),DataExtraction(T.right,Ct))

7:end if

算法4DataFilter(F,Ct,N)

Input:F-an iDEForest,Ct-depth threshold,N-filter threshold

Output:KNNsearch_space

1:Initializecandidate_data,search_space

2:forTinFdo

3:candidate_data=candidate_data∪DataExtraction(T,Ct)

4:end for

5:(value,counts)←count(condidate_data)

6:ifcounts≥Nthen

置于公共空間中的雕塑藝術，一般是以公共藝術的形態存在的，這種方式由來已久。但把來自國內外11個國家的雕塑，以一種公共藝術的方式介入到沙漠之中，并永久性安置于沙海之地，可以說，目前在世界范圍內尚屬首例。

7:search_space=search_space∪value

8:end if

9:returnKNNsearch_space

2.2 第二階段ASC

根據LOF的思想,計算每個測試點的局部利群因子,其中k近鄰的搜索空間不再是全部數據集而是由iKSSE提取所得的子集。異常分數計算分為兩步:

第一步,在iKSSE提取所得搜索空間中實例化每個樣本點的k近鄰數據,以及他們到樣本點的距離,將所得結果保存在數據庫M中;

3 前置iKSSE的優越性

相對于LOF算法,iDELOF算法前置iKSSE,借助隔離的思想快速提取位于簇中心的子集作為ASC近鄰數據搜索空間,具有以下優越性。

3.1 拉大正異常點局部離群因子之間的差距

對位于簇周圍的異常點p,其Fmin(p)、Fmax(p)增大,而Smin(p)、Smax(p)不變,因此異常點的LOF值增大;而對位于簇深處的正常點o,即其所有k近鄰都在簇中,并且其k近鄰的所有k近鄰點也都在簇中的點,其Fmin(o)、Fmax(o)和Smin(o)、Smax(o)均改變不大,因此正常點的LOF值也變化不大。因此iDELOF算法拉大了正異常點LOF值之間的差距,使異常檢測變得更容易。為進一步說明,圖1和圖2列舉了一個簡單的例子,其中k取2。

圖1 加入iKSSE前后p點LOF的取值范圍

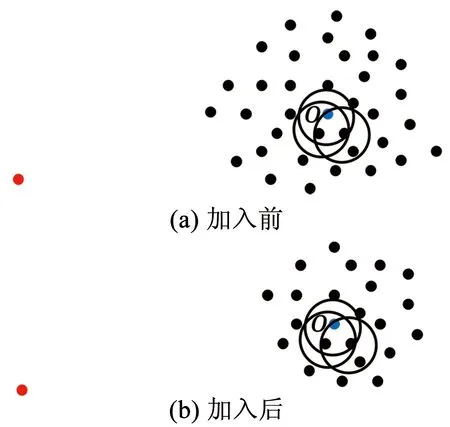
圖2 加入iKSSE前后o點LOF的取值范圍

3.2 增強對交叉異常的識別能力

對于LOF算法,簇中心與邊緣樣本點的LOF值相差不大,因此該算法無法有效識別此類交叉異常,當簇的密度變化不大時,LOF將退化為隨機檢測器。對于iDELOF算法,只有位于簇深處樣本點o的LOF值是相同的,而簇內其余點p的Smin(p)、Smax(p)雖然變化不大,但Fmin(p)、Fmax(p)隨著與中心距離由近至遠逐漸增加,因此LOF值也隨之增加,呈階梯分布,這使得算法更有可能將位于數據集邊緣的樣本點識別為交叉異常,而不是盲目地從整個數據集中隨機識別。為進一步說明,圖3和圖4列舉了一個簡單的例子,其中k取2,紅色點為交叉異常點,黑色點為正常點。

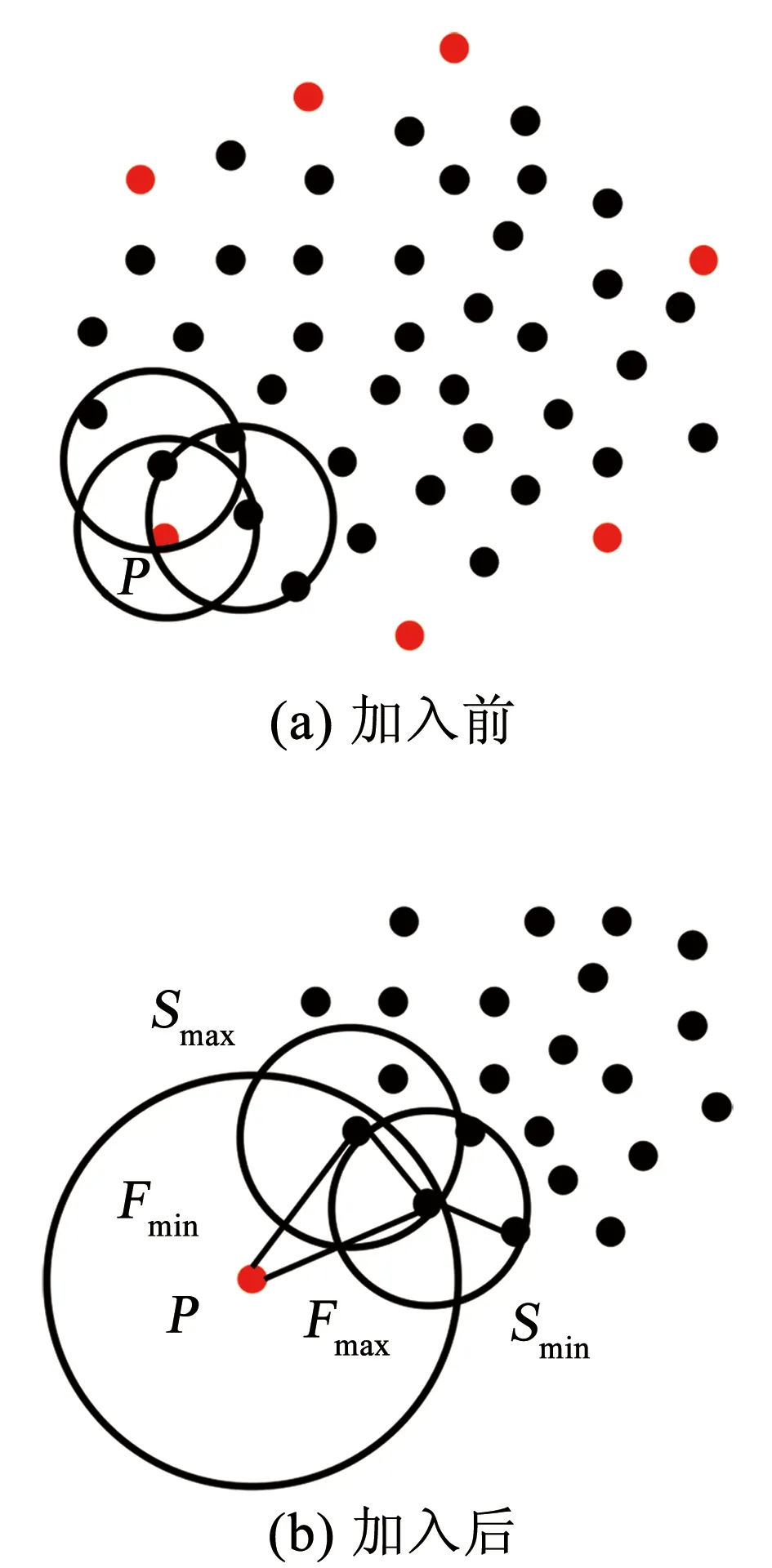
圖3 加入iKSSE前后p點LOF的取值范圍

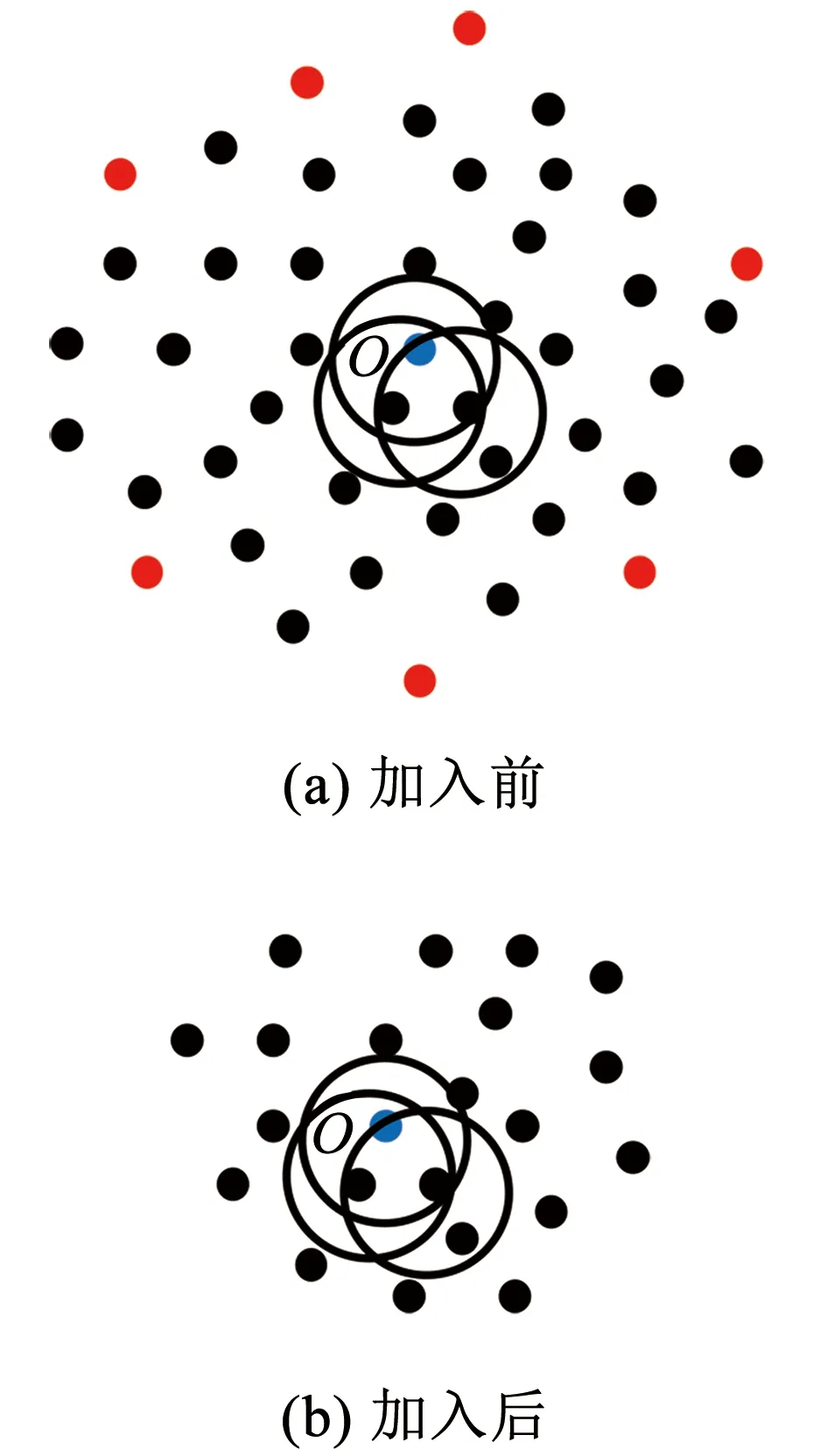
圖4 加入iKSSE前后o點LOF的取值范圍

3.3 增強低密度簇周圍異常點的識別能力

對于 LOF算法,在Fmin(a)、Fmax(a)相同的前提下,顯然低密度簇周圍異常點比高密度簇周圍異常點的Smin(a)、Smax(a)更高,其LOF值相應的更小,因此也更容易被LOF忽略。對于iDELOF算法,圖5為數據提取森林中深度的等高線圖,從圖中可以看出當深度閾值Ct固定時,加入iKSSE后,對于近鄰數據的搜索空間,其低密度簇半徑的縮減量大于高密度簇,也就是說在Smin(a)、Smax(a)不變的情況下,顯然低密度簇周圍異常點比高密度簇周圍的異常點的Fmin(a)、Fmax(a)增加的更多,因此兩者LOF值之間的差距減小,改善了LOF對存在于不同密度簇周圍異常點的識別偏差。

圖5 各數據點在數據提取森林中的深度等高線

3.4 降低時間和空間復雜度

3.4.1 時間復雜度

對于iKSSE階段:假設建立t棵樹,每棵樹的采樣大小為ψ,則時間復雜度為O(tψlogψ),獨立于樣本大小以及空間維度,只在模型訓練時提取一次。

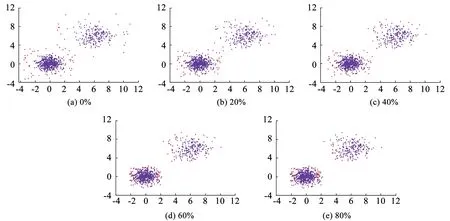
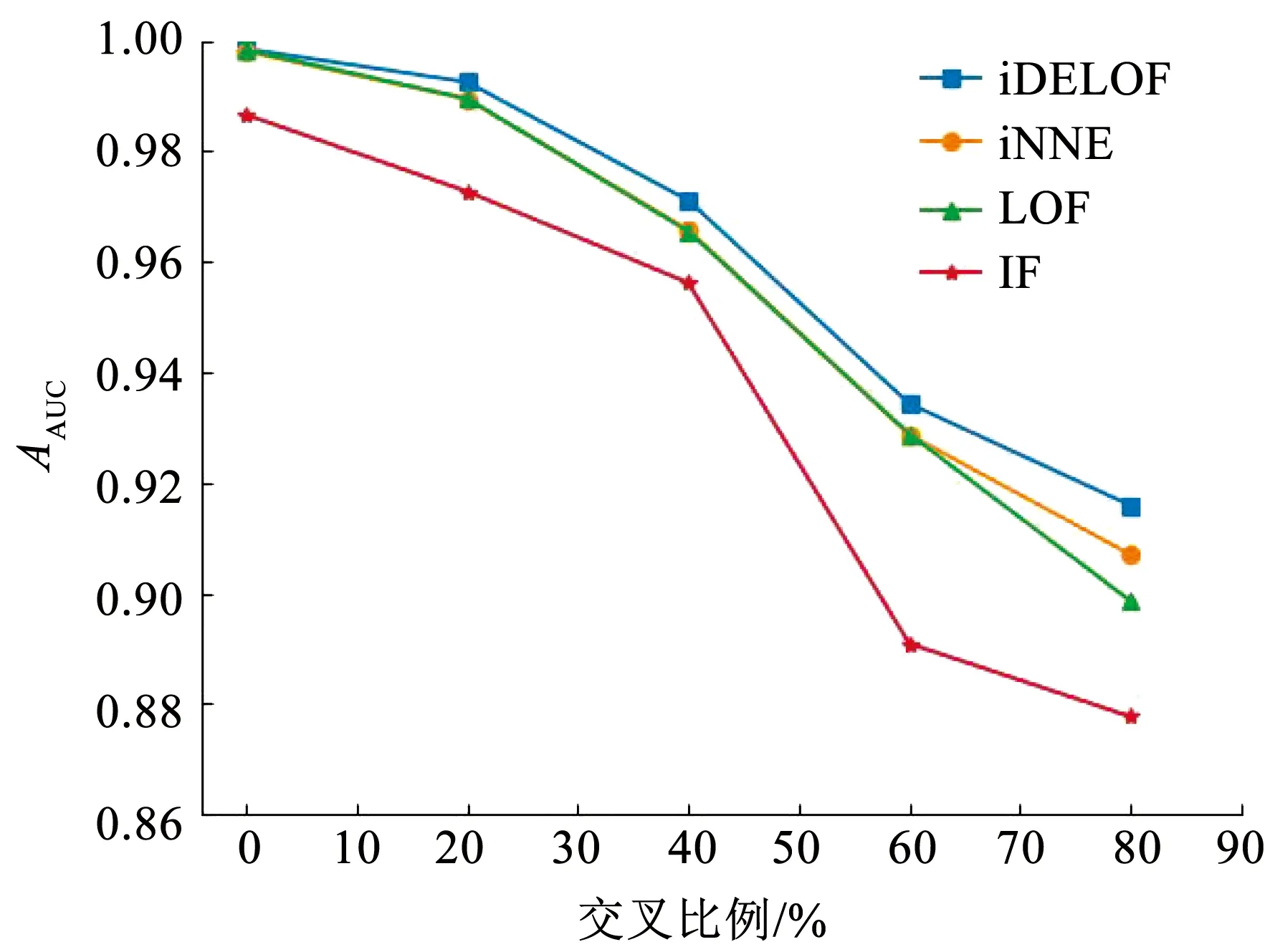
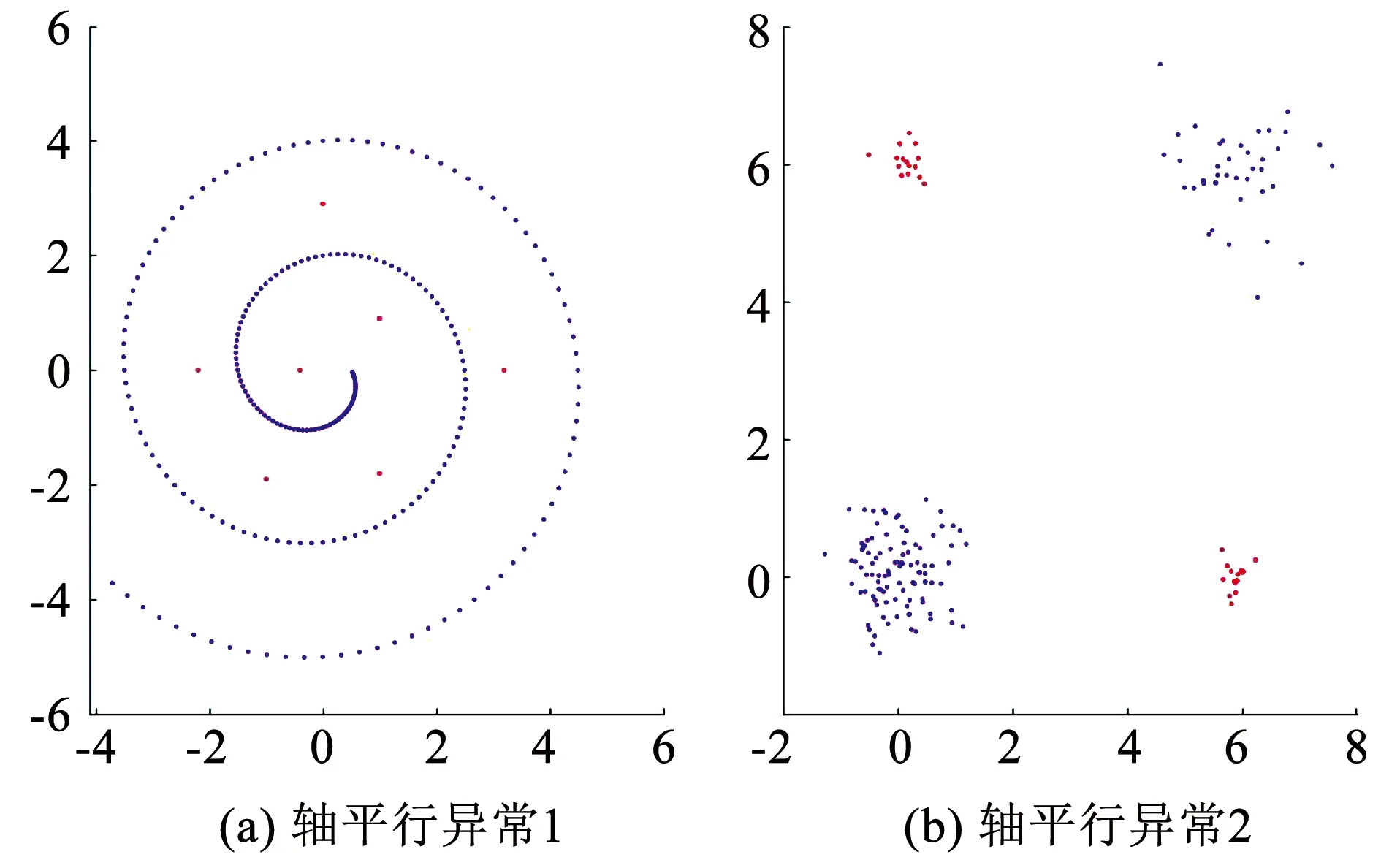
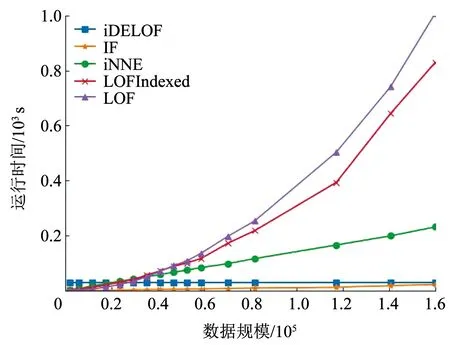
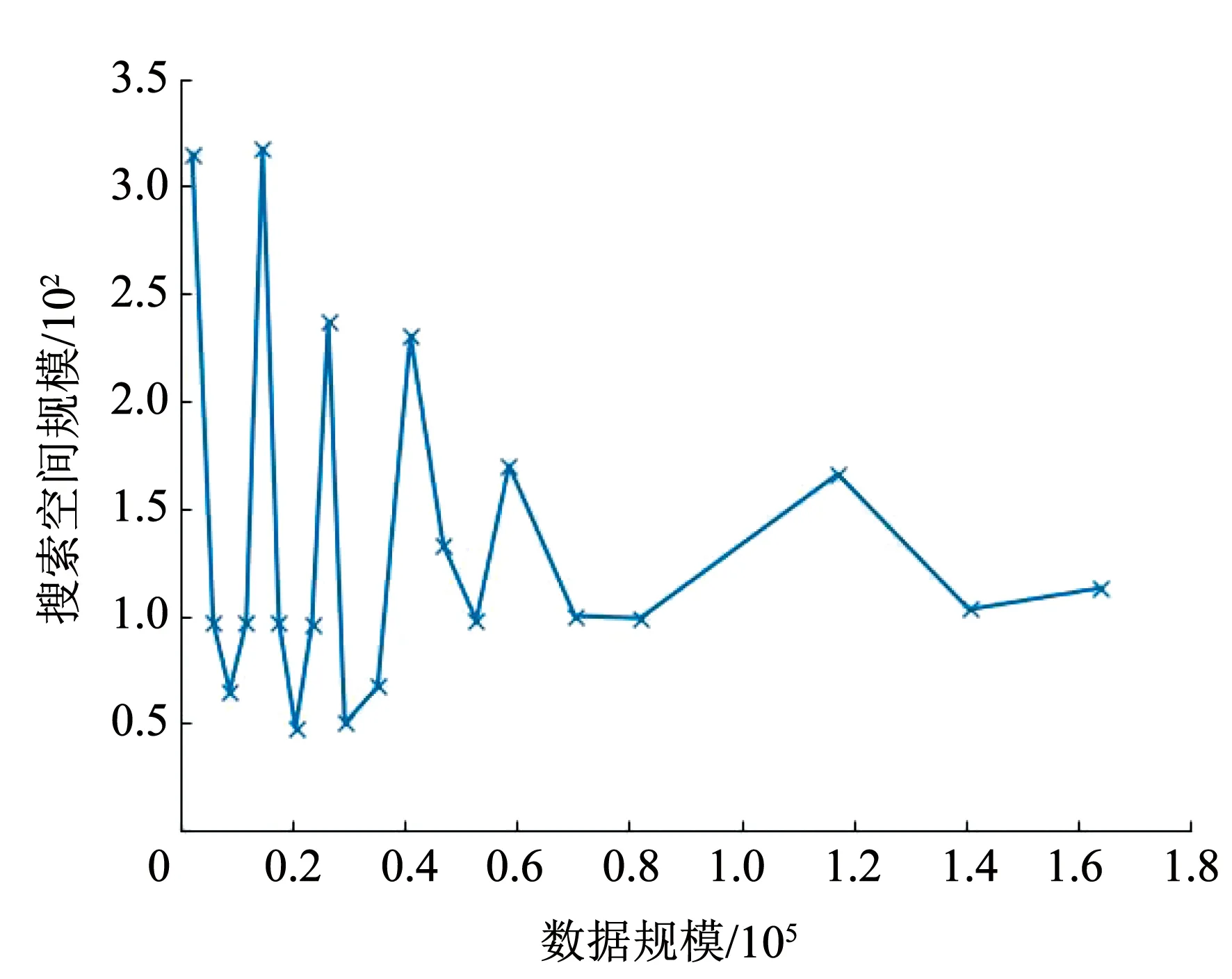
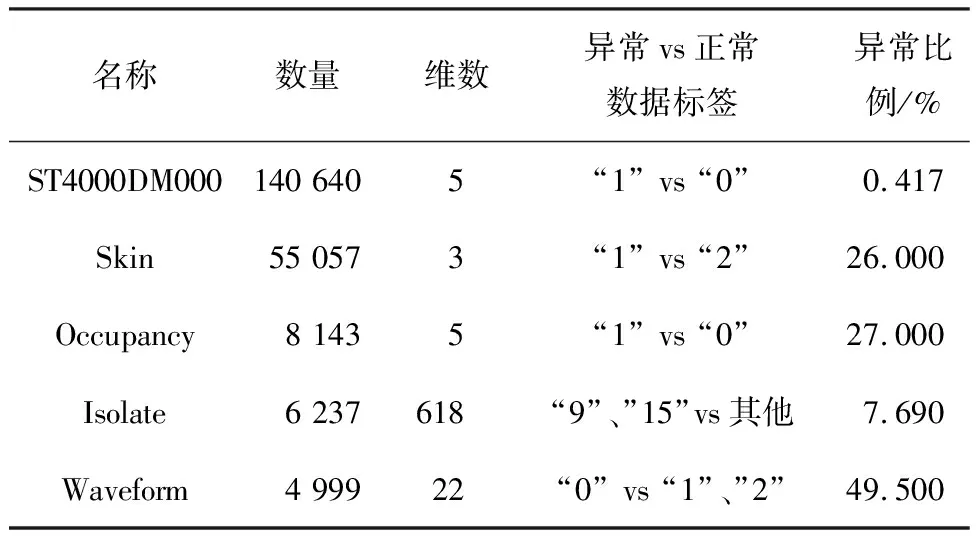
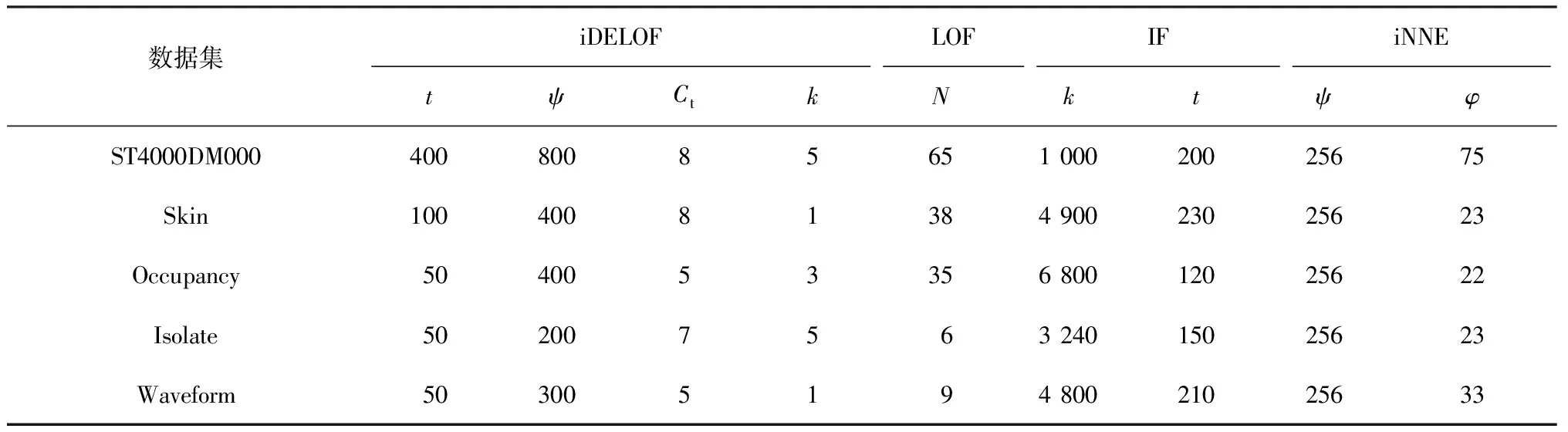
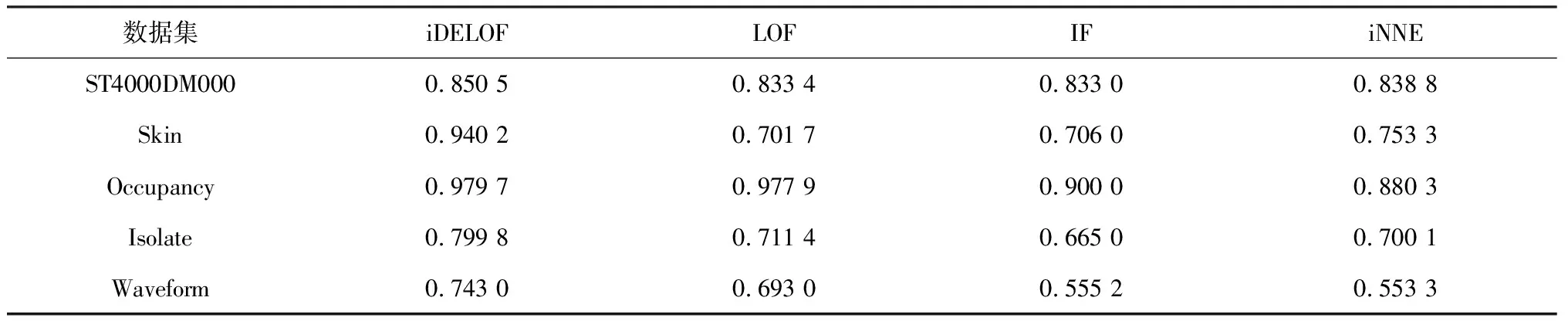
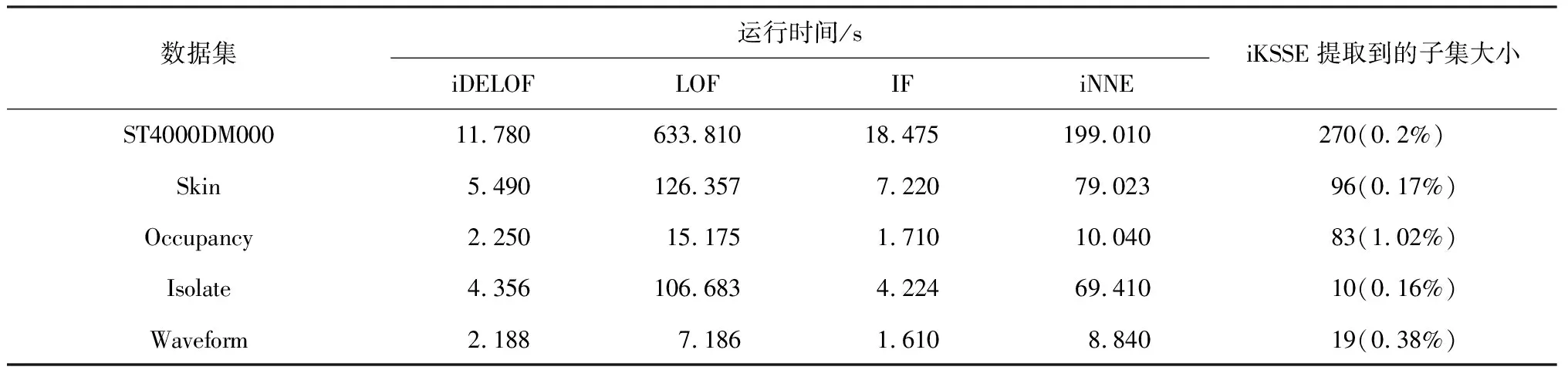
對于ASC階段:不同于LOF算法,iDELOF算法是在iKSSE提取到的子集上進行k近鄰搜索,因此每個估計器的時間成本是O(n·m),并且iDELOF只有一個基估計器,因此算法的時間成本就是O(n·m),其中n為數據集大小,m為iKSSE提取到的子集的大小(0

綜上算法的整體時間復雜度為O(tψlogψ)+O(n·m),可以看出iDELOF有效地將LOF的時間復雜度降低到與樣本數量呈線性關系且該線性關系的斜率很小,并且樣本數量越大,iKSSE的時間耗費相較于其他算法就變得越微不足道,整個算法在時間復雜度上的優越性也就越明顯。因此本文算法更適合應用于超大規模的數據中。

3.4.2 空間復雜度

對于iKSSE階段:假設建立t棵樹,每棵樹的采樣大小為ψ=2a,則每棵樹最大的節點數為Nnode=2a+2a-1+…+20,因此所需內存為O(t·Nnode),獨立于樣本數量,對于計算機來說微不足道。對于ASC階段:iDELOF算法是在iKSSE提取到的樣本子集上進行k近鄰搜索,因此可以有效地將所需內存減小到O(m2)。

綜上,算法整體的空間復雜度為O(t·Nnode)+O(m2),遠小于LOF,且不會隨著樣本數量的增加而持續上漲,因此算法可以很容易加入在線學習的模塊,應用于數據流中。

4 實驗驗證

進行了4組實驗,每組實驗分別進行iDELOF算法與LOF、IF、iNNE(isolatin using nearest neighbour ensemble)[14]3種典型算法的對比分析,以驗證iDELOF算法的優越性及其應對真實數據集的能力。其中前2組實驗采用合成數據集,驗證iDELOF算法在識別交叉異常以及軸平行異常方面的優越性;第3組實驗采用Backblaze上公開的磁盤數據集,驗證當數據集規模不斷增大時iDELOF算法在時間復雜度上的優越性;第4組實驗采用Backblaze和UCI上多個公開數據集,測試iDELOF應對不同維度、異常比例及數量級的真實數據集的能力。各種算法的超參數均根據數據集調整到最佳組合,其中iDELOF、IF以及iNNE為隨機算法,他們的AUC值(AAUC)均采用10次不同的隨機數種子計算所得平均值。

4.1 交叉異常的識別

主要測試各種算法對交叉異常的識別能力。采用合成數據集,包括2個密度不同的正常數據簇,異常數據分布在正常簇周圍并且存在一定交叉。其中低密度簇包含200個樣本點,周圍存在20個異常點;高密度簇包含500個樣本點,周圍存在40個異常點。異常點在固定環寬的圓環中隨機生成,根據圓環邊界與正常數據邊界圓環交叉程度的不同,生成5組不同的數據集,分別表示不同的正異常數據交叉比例,見圖6。

圖6 不同交叉比例的測試數據集

圖7為4種算法的AAUC隨著交叉比例的變化趨勢。從圖中可以看出隨著交叉比例的增大,各個算法的識別能力都有所下降,其中iDELOF一直擁有著最高的AAUC,且隨著交叉比例越大,iDELOF與其他算法之間的差距也越大,識別優越性越明顯。

圖7 各算法在不同交叉比例下的AAUC

4.2 軸平行異常的識別

主要測試各種算法對軸平行異常的識別能力。實驗采用2組軸平行異常的數據集,數據集1見圖8(a),正常數據呈螺旋形分布,其中隱藏著6個異常點,數據集2見圖3(b),圖中左下和右上角為2個呈高斯分布的密度不同的正常數據簇,左上和右下角為2個異常數據簇。

圖8 軸平行異常測試數據

圖9為各數據點在不同算法下所得LOF值的等高線圖。從圖中可以看出,RC(robust covariance)及IF算法的識別效果非常差,這是由于IF基于正常數據點的投影進行分割,因此對此類隱藏在軸平行中的異常點無能為力,iNNE的識別效果也不理想。而對于iDELOF以及LOF算法,只要調整好近鄰數據k的大小便可以很好刻畫出正異常點的分界。因此雖然加入iKSSE,iDELOF本質上依然為基于相對密度的算法,與LOF算法一樣在識別軸平行異常方面具有明顯優越性。

4.3 時間復雜度測試

主要驗證iDELOF算法在時間復雜度方面優越性。采用的數據集為Backblaze 2015年ST4000DM000型號的磁盤數據,數據集規模為1 000～250 000。采用的方法為對比各算法檢測磁盤異常所需運行時間隨樣本數量的變化情況,其中LOF算法根據是否使用R_tree[15]分為LOFIndexed以及LOF算法。

圖10記錄了各算法的運行時間隨數據集規模的變化趨勢,圖11記錄了iKSSE在不同規模磁盤數據集下提取到的子集的大小。從圖10可以看出IF、iNNE以及iDELOF算法的時間復雜度與數據集大小呈線性關系,LOF算法的時間復雜度則與數據集大小的二次方成正比,而LOFIndexed算法利用R_tree對k近鄰進行快速檢索,時間復雜度相比線性掃描方法有所降低,但當樣本數據量增大時,運行時間依然很大。從圖11可以看出隨著磁盤數據集規模的擴大,iKSSE提取到的子集的大小m不會隨之增加,而是穩定在100附近。因此雖然在數據量較小時,iDELOF由于加入iKSSE步驟,運行時間比其他幾個算法略長,但是當樣本數量逐漸增多時,算法在時間復雜度上的優越性就體現出來了:iDELOF的運行時間隨著樣本規模增大而增加緩慢,其時間曲線的斜率m比最有效率的IF算法都要小。當樣本的數量達到25 000時,iDELOF算法的運行時間已經遠遠小于LOF算法;當樣本數量達到250 000時,iDELOF算法的運算速度已經逼近IF算法,并且可以預測隨著樣本規模的進一步擴大,iDELOF算法在時間復雜度上的優越性也會體現得越明顯,成為最有效率的算法。

圖10 各算法在不同規模數據集下的運行時間

圖11 iKSSE在不同規模數據集下獲得子集的大小

4.4 真實數據集測試

主要驗證iDELOF算法應對真實數據集的能力。采用包括Backblaze和UCI上不同維度、異常比例及數量級共5個公開數據集。每個數據集的大小、緯度、處理方式以及異常比例見表1。各個算法的超參數采用網格搜索法得到最佳組合見表2。不同算法在不同數據集上的AAUC值以及對應的運行時間記錄見表3和表4。iKSSE在不同數據集上提取到的子集大小記錄見表4。

表1 實驗數據集信息

表2 各算法在不同數據集上的最佳參數

表3 各算法在不同數據集上的AAUC

表4 各算法的運行時間以及iKSSE提取到的子集大小

對于檢測精度,從表3中可以看出iDELOF在多個不同真實數據集上均被證實擁有最優的AAUC,在離群點檢測精度方面優越性明顯。對于運行效率,從表2中可以看出LOF算法在多數大規模數據集上都需要很大k值才可以達到較好的檢測效果,因此該算法的時間復雜度是所有算法中最高的。iDELOF算法由于前置了iKSSE,從各個數據集中提取到的子集的大小只占整個數據集的1%左右(見表4),這使得算法僅需要個位數的k值(見表2)就可以達到很好的效果。因此iDELOF在多數數據集上都保持著較小的時間復雜度(見表4),只在最后3個數據集上運行時間比IF算法稍慢,這主要是數據集規模較小,算法的優越性沒有完全體現的原因。

5 結 論

iDELOF異常檢測算法將基于隔離思想的近鄰搜索空間提取前置于LOF算法,高效剪切掉大量無用及干擾數據,獲得更加精準的搜索空間。研究表明:

1)iDELOF異常檢測算法拉大了正異常點局部利群因子的差距,增強了對交叉異常及低密度簇周圍異常點的識別能力,提升了檢測效果。

2)iDELOF異常檢測算法在識別軸平行異常方面,與LOF一致,具有明顯的優越性。

3)iDELOF異常檢測算法通過iKSSE獲得的子集顯著小于原數據集,且多數子集數據量小于原數據集的1%,因此iDELOF的時間空間復雜度顯著降低。

4)原數據集數據量越大,iDELOF異常檢測算法在時間復雜度上的優越性越明顯;當樣本數量達到一定數值時,iDELOF算法的運行時效將高于IF算法。

5)不同緯度、規模、異常比例真實數據集實驗表明:iDELOF算法在異常點檢測精度及運行效率方面顯著優于其他先進算法。