構網型風電-串補輸電系統的次同步振蕩特性分析

郝錦文，馬永光，孫大衛

（1.華北電力大學 自動化系，河北 保定 071003；2.國網冀北電力科學研究院（華北電力科學研究院有限責任公司），北京 100045）

0 引言

隨著風電并網比例的不斷增大和大規模電力電子裝置的集成，電網表現出低短路比的特征。在這種電網環境下，由于目前應用于實際的風電并網變流器采用的基本都是跟網型控制，所以跟網型變流器與外部電力系統之間可能發生交互作用[1-3]，包括與線路串補、高壓直流輸電與弱交流電網的相互作用，從而引發復雜的小干擾振蕩問題[4,5]。另外，雙饋風機經串補電路送電時[6]，經常因感應發電機效應導致次同步諧振（Sub-synchronous resonance，SSR），故工程實際中大量應用直驅風電機組。同時，內部不同變流器之間亦可能發生交互作用，包括變流器參數整定不當造成的振蕩失穩或變流器之間的動態交互，從而引發電力系統在弱電網環境下的小干擾振蕩問題。

國內外學者關于電力系統在弱電網下的小干擾振蕩方面的研究已經取得了一些進展。學者們以同步發電機的物理機理為基礎，提出了構網（Grid type）變流器的概念，可為弱電網提供相應的頻率和電壓支撐。構網變流器等效輸出阻抗小，在低頻段表現為與電網相同的相位特性，具有較強的弱電網適應性，相比跟網型變流器，可以在很大程度上減少在弱電網下的SSR 振蕩問題。文獻[7]以實際工程為例，對比了構網型和跟網型變流器在弱電網下的并網適應性差異以及不同控制參數對穩定性的影響趨勢；文獻[8]指出了在配比一定時構網型機組可以改善風場在弱電網下的次同步振蕩問題。

雖然構網型變流器在弱電網下穩定性較好，但不代表其適用于各種工況。文獻[9]指出構網型變流器經串補電網時，輸出阻抗在不超過電網的額定頻率段內表現出負阻尼特性。若串補線路的振蕩頻率也在此頻率段內，則容易產生SSR 振蕩。文獻[10]指出在強電網環境下，由于各個電壓源之間的聯絡阻抗比在較小，構網型變流器會使得電壓源并聯難度增大，從而振蕩加劇。為了全面研究構網型變流器的并網適應性，需要在各種穩定性較差的工況下對其進行完整的穩定性分析。

本文在Simulink 仿真軟件中建立了1.5 MW構網型直驅風機的串補輸電系統模型，然后將某風電場等效成1 臺永磁直驅風機，通過掃頻得到風場1～100 Hz 的阻抗特性。然后，用伯德圖來分析系統的穩定性，重點分析了電網強度、串補度、風機數以及關鍵控制參數對構網型直驅風機并網系統次同步振蕩阻尼的影響。

1 構網型直驅風機串補系統建模

為了實現串補系統的穩定控制，首先需要對系統進行建模，同時分析出影響系統不穩定的因素。

本文以某風電場為算例進行建模型分析。近年來，該風電場通過加入串補線路進行遠距離輸電。以其中1 個風電場為例，其輸電系統如圖1所示。圖中，風電經690 V 輸電線路，通過變壓器后又經2 條35 kV 的串補線路，最后通入電網。將變壓器等效成一字等效電路，然后和系統阻抗串聯，等效后的串補度為33.41%。假定風電場內的風機運行工況接近，所有直驅風電機組容量均為1.5 MW，故所有風機的串聯和并聯可看作一臺直驅風電機組。

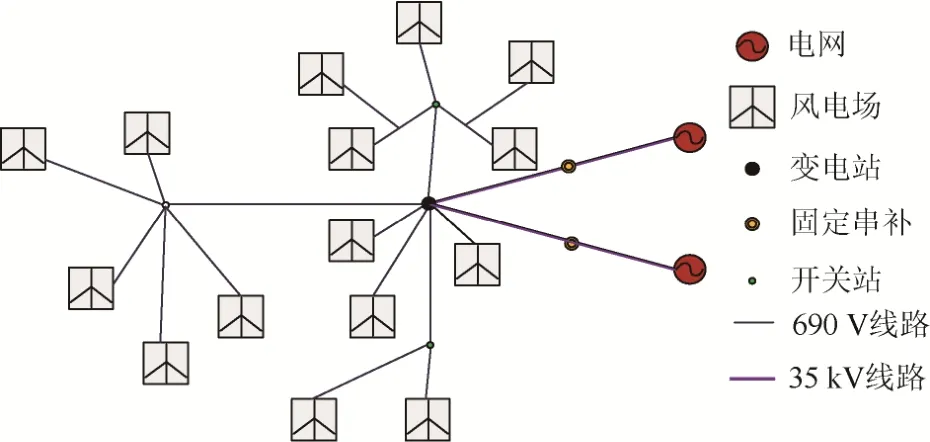
圖1 風電場輸電系統Fig. 1 Wind farm electric power transmission system

圖2 是等效后的直驅風電機系統結構圖。圖中，Pn為風機的額定功率；Pm為機側變換器輸出功率；Pg為網側變換器輸出功率；udc為直流電壓；Cdc為直流電容，Rg為線路等效電阻；Lg為線路等效電感；C為串補電容；Qg為網側變換器輸出的無功功率。風電機組采用永磁同步發電機[11,12]（Permanent magnet synchronous generator，PMSG）經構網型變流器并網，而構網型變流器包含機側變流器和網側變流器，交流電網用阻抗和理想電壓源進行等值。

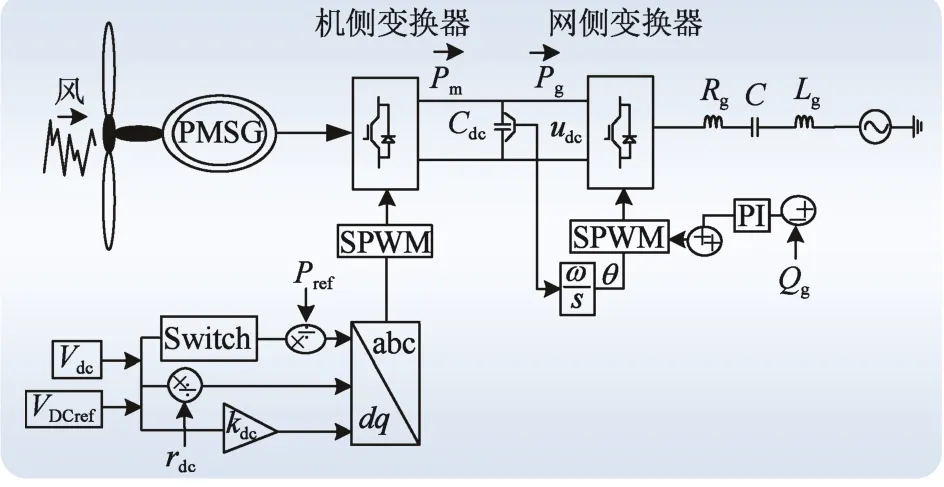
圖2 構網型直驅風機控制結構Fig. 2 Grid type direct-driven wind turbine control structure

在網側變換器中，直流側電壓udc被輸入到積分環節。該控制器的輸出作為網側變換器輸出電壓ug的相位θ，用于脈沖寬度調制（Pulse width modulation，PWM），從而使直流電壓udc側與網側變換器輸出角頻率相同。PWM 還可以間接控制網側變換器輸出的無功功率Qg。在機側變換器中，檢測值Vdc和設定值Vdcref經過閾值后與Pref相除以控制Ia、Vdc與rdc的差，Ib、Vdc和Vdcref的差經過增益kdc控制Ic。在機側變換器中，增加的Vdc自調節反饋可以看作下垂系數，以避免失穩。

2 風電串補系統的振蕩風險分析

2.1 基于阻抗分析法的機理分析

阻抗分析法原理是在靜止坐標系或dq坐標系下，將直驅風電機組等效看作由電抗、電納和電阻組成的電路結構[13]，然后建立系統的小信號阻抗模型，利用伯德圖進行判穩。

等效的電網阻抗和風電機組阻抗幅值交點所對應的頻率為諧振頻率，其決定了系統的穩定性。機組的轉子側變流器和網側變流器采用相似的控制結構。當機組僅流過工頻電流時，這些控制器能夠保持正常運行。但是，如果在特定工況下存在諧振點，則等效的LC 諧振將會引起振蕩電流分量，進而導致機組控制系統在當前頻率下對位呈現負電阻-電抗特性。此時可以通過判斷相角裕度的正負來判斷正負電阻-電抗特性。如果諧振點處的相角裕度大于零，則可判斷系統阻抗呈“正電阻+電抗”的特性，此時系統沒有次同步振蕩風險；反之有次同步振蕩風險。

本節將搭建構網型直驅風機串補輸電仿真系統，并在此基礎上初步探討算例地區并網風機數量對系統SSR 特性的影響。

風機并網系統參數如表1 所示。

表1 風機并網系統參數Tab. 1 Parameters of wind turbine grid connected system

2.2 風電串補系統的SSR 仿真

通過Simulink 搭建了風場經串補系統的等值模型。每臺風機容量均為1.5 MW，風電場總裝機容量為若干兆瓦到上百兆瓦不等。

風速為1 m/s 時，對并網風力機數量為1 臺和10 臺時的工況進行仿真驗證，其相電流波形如圖3 所示。

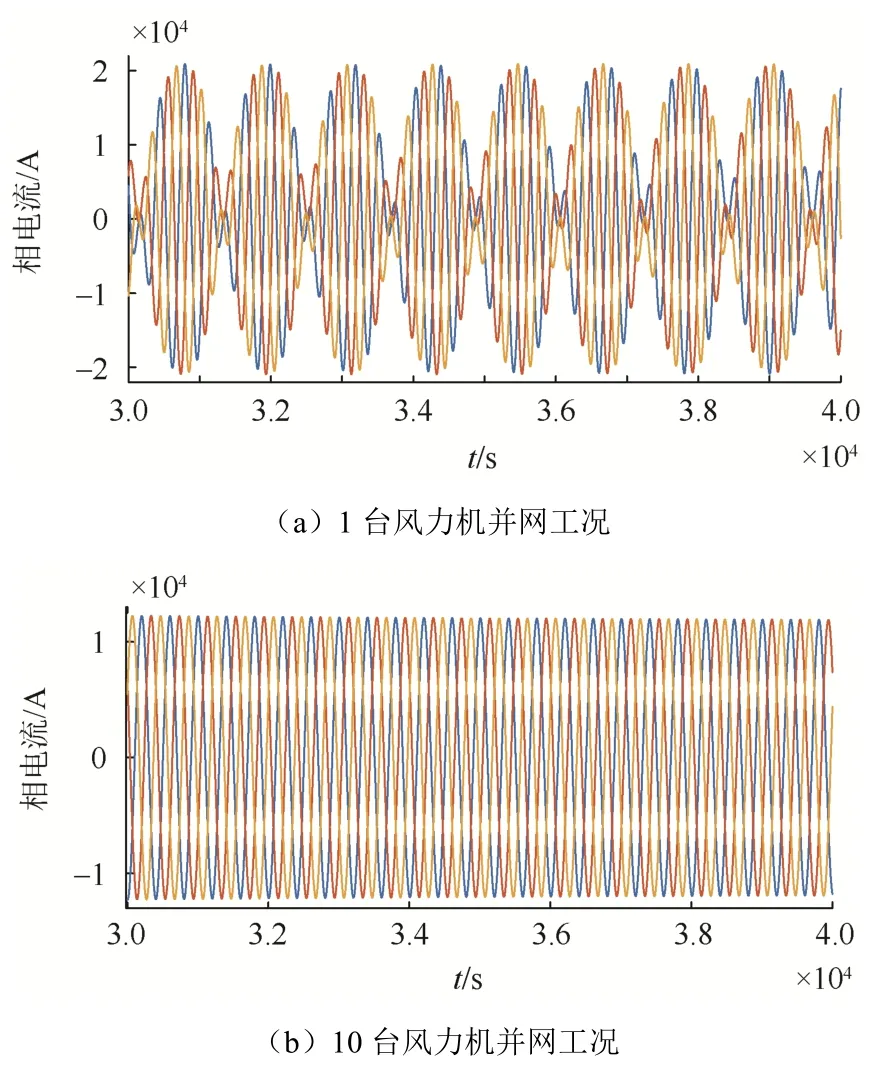
圖3 不同數量風電機組接串補線路電流波形Fig. 3 Current waveform of different numbers of wind turbines connected in series

由圖3 可知，當有1 臺風電機組并網時，系統產生振蕩；并網風電機組的數量增加到10臺后，系統不會產生振蕩。由上述現象可作出假設，增加并網風電機組的數量可能會減小SSR 諧振的風險，使系統穩定性變好。

2.3 SSR 特性與風電機組數量關系分析

為了得到衡量系統穩定性的相角裕度指標，對系統進行掃頻。掃描出風機在1～100 Hz 內每隔1 Hz 的阻抗特性，并作出加入33.41%串補的等值電網阻抗。1 臺和10 臺數量風電機組阻抗的伯德圖如圖4 所示。

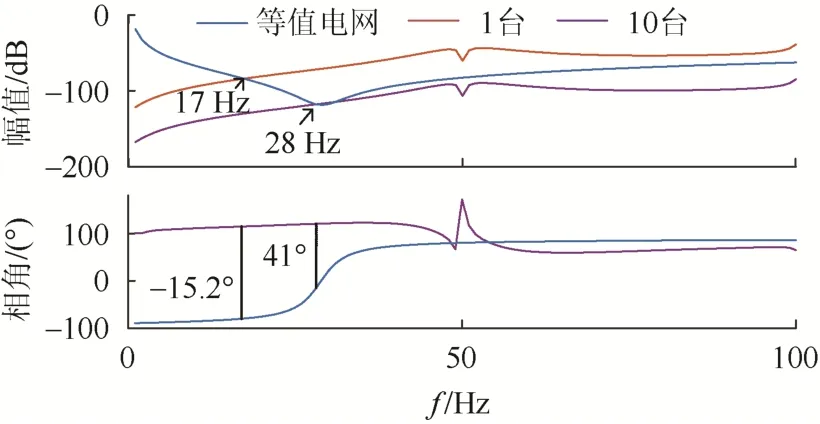
圖4 有串補時電網阻抗和風機阻抗伯德圖Fig. 4 Bode diagram of grid impedance and fan impedance with series compensation time

由圖4 知，電網阻抗與2 條風電機組阻抗交點處的頻率分別為17 Hz 和28 Hz。當并網風機為1 臺時，系統相角裕度小于零，有振蕩風險。增加到10 臺后，系統相角裕度大于零，無振蕩風險。圖4 的分析結果表明，當并網風機增加后，風電機組阻抗和電網阻抗相位曲線基本不變，幅值曲線平行下移，與此同時，阻抗的交點向右偏移。在1～20 Hz 內，串補電網的阻抗線路的相位曲線緩慢上升，系統呈容性，且相角一直處于小于零的水平，系統存在SSR 風險；在20 Hz 之后的一段時間內，電網阻抗的相位由容性變化為感性，且風電機組的相位曲線變化增大，導致2 條相位曲線的相角差變小，相角裕度增大，系統逐漸穩定。

3 小干擾穩定影響因素仿真

研究結果表明，構網型風機雖然在弱電網下具有良好的穩定性，但并不適用于強電網環境[10]。為了全面研究構網風機的并網適應性，本節討論系統在有無串補時，隨著并網風機的增加，電網強度變化對SSR 風險影響，以及在穩定性十分惡劣的工況下，風速、直流電壓與輸出轉速比值對系統穩定的影響。

3.1 不同電網強度下SSR 風險和風機數量關系

PMSG 接入電網的強弱通常采用系統等值電抗值或短路比表示。系統等值阻抗越小，短路比越大；系統等值阻抗越大，短路比越小。短路比表達式為：

式中：UN為系統的額定電壓；Z為系統等值阻抗；SG為單臺風機容量。

首先在無串補時，觀察系統的振蕩情況。在短路比為1 和100 的情況下，由掃頻得出風機在1～100 Hz 內每隔1 Hz 的阻抗曲線。然后，畫出等值電網阻抗與1、10、100 和1 000 臺風機的阻抗的伯德圖。經分析得出結論為：在無串補時，電網強度的增大和風機數量的增多，對系統都不會造成SSR 風險。

3.2 串補度對諧振風險影響分析

由上述分析可知，系統不存在發生次同步諧振風險，故進一步改變系統的線路參數，來觀察穩定性變化情況。

串補度又稱線路串補電容補償度，用k來表示。串補度主要由線路中電感L、電容C決定，具體數學表達式可以表示為：

線路阻抗的模值如式（3）所示：

當f=50 Hz，R=2.65×10-4Ω 時，在短路比為200 的情況下，改變電感L、電容C使串補度分別為26.73%、33.41%、44.55%、66.82%。以100 臺風機為例，不同串補度條件下風機并網系統的電流曲線如圖5 所示。

從圖5 可以看出，在加入串補后，當有100臺風電機組并網時，系統會產生不規律振蕩；并且隨著串補度的增加，相電流振蕩更加劇烈。所以，有必要分析系統的相角裕度。不同串補度下線路阻抗、風機阻抗的伯德圖如圖6 所示。

圖5 不同串補度下100 臺風機并網電流曲線Fig. 5 Grid-connected current curves of 100 fans with different series compensation degrees

圖6 不同串補度下電網阻抗和風機阻抗伯德圖Fig. 6 Bode diagram of grid impedance and fan impedance under different series compensation degrees

由圖6 可知，4 條等值電網的阻抗幅值曲線均與100 臺的風電機組阻抗幅值曲線相交，交點處頻率分別為15 Hz、17 Hz、20 Hz、24 Hz，交點處頻率對應的等效系統的相角裕度分別為-13.3°、-15.2°、-17.8°、-21.8°。系統均存在次同步諧振風險，且相角裕度依次減小。

由式（3）可知，串補度的改變，即串補電容改變時，阻抗模值Z會隨之改變，導致線路的幅值總體上移。

3.3 有串補時，不同電網強度下SSR 風險和風機數量關系分析

改變仿真模型中690 V 線路的電感值和電容值，確定不同系統短路比為自變量，觀察不同電網強度下的線路阻抗和風電機組阻抗的伯德圖，如圖7 所示。

圖7 不同串補度下相角裕度與電網強度關系Fig. 7 Relationship between phase margin and grid strength under different series-compensated level

由圖7 可見，串補度對穩定性有負面作用。當電網強度增大，不同串補度下的相角裕度也一直呈下降趨勢，最后趨于平緩。在串補度為66.8%時，系統始終處于不穩定狀態。這說明串補度和電網強度都對SSR 特性有著負面的干擾。

在串補度提升后，具體分析機組在分別接入強弱電網下風機數量與相角裕度的關系。取短路比典型值分別為2、20、200。

圖8 示出了短路比為2 時，不同串補度下的相角裕度與風機數量關系。

圖8 短路比為2 時不同串補度下的相角裕度與風機數量關系Fig. 8 Relationship between phase margin and wind turbine number under different series-compensated level with a SCR of 2

由圖8 可知，當短路比為2 時，系統在弱電網下有著較好的穩定裕度。相角裕度在1 臺風機并網時開始增加，且串補度小的系統相角裕度起點較高，上升的斜率較大。當串補度為13.36%，系統并入2 臺風機時，系統已經達到了穩定；系統并入10 臺風機時，4 個串補系統均達到了穩定。串補度為13.36%時系統達到了最大穩定度，其他3 條曲線的相角也相繼達到最大（由于穩定性較好，相角裕度很快達到180°，故刪減了一部分曲線）。

圖9 示出了短路比為20 時，不同串補度下的相角裕度與風機數量關系。

圖9 短路比為20 時不同串補度下的相角裕度與風機數量關系Fig. 9 Relationship between phase margin and wind turbine number under different series-compensated level with a SCR of 20

由圖9 知，短路比為20 時，由于電網強度的增大，穩定性開始下降。在并入1 到10 臺風機之間，相角裕度無明顯變化，串補度較大時，甚至呈下降趨勢。當風機數量大于10 臺時，不同串補度系統的相角裕度都以不同的上升速度增大，串補度小的同樣很快到達了穩定。串補度為66.82%的系統，在風機并入100 臺后達到穩定。

圖10 示出了短路比為200 時，不同串補度下的相角裕度與風機數量關系。

圖10 短路比為200 時不同串補度下的相角裕度與風機數量關系Fig. 10 Relationship between phase margin and wind turbine number under different series-compensated level with a SCR of 200

由圖10 知，短路比為200 時，電網強度進一步增大。可以發現，在風機并入量在100 以內時，相角裕度在任何一個數量的風機下，都沒有初始點大，期間系統經過了一個相角裕度減小再增大的過程，直到風機數量達到100 臺后，相角裕度才開始增大。

分析圖8～10 可以發現，4 條曲線與風機數量之間呈現正相關的關系，且串補度越高，影響越顯著。

由上述分析可知，構網型風機在弱電網環境下有著較好的小干擾穩定性，隨著電網強度的增大，會有失穩的風險。圖10 表明，系統的穩定裕度會隨著風機數量的增加，先減小再增大。

3.4 有串補時不同風速下SSR 風險和風機數量的關系分析

以上內容分析了當風速為1 m/s 工況時風電場系統相角裕度與并網風電機組數量的關系。為了進一步研究兩者之間的關系，同樣將系統加入一定量的串補，在風速減小一定比例條件下，研究其相角裕度變化規律。

不同風速下，相角裕度與風機數量關系如圖11 所示。

由圖11 可以發現，在構網型風機并網數量相同時，風速越大則系統相角裕度越小。隨著風機數量的增多，在各個風速下系統呈現出穩定性先下降再上升的過程[14,15]。對于各個風速工況，在風機并入數量達到100 臺時，系統相角裕度均到達最低點。最終相角裕度在大于零后繼續上升。

3.5 有串補時，不同U 與ω 比例下SSR 風險和風機數量的關系分析

圖12 示出了不同U與ω比例下，相角裕度與風機數量關系。

圖12 不同U 與ω 比例下相角裕度與風機數量關系Fig. 12 Relationship between phase margin and wind turbine number under different U and ω proportion

由圖12 可知，以粉色曲線為基準線，縮小U與ω的比，能很好地提升系統的穩定性。當比值縮小為0.1 時，即使在89.1%的高串補度和強電網下，系統相角裕度的最低點值仍比較大。在此基礎上，U與ω比例增大到0.5 時，相角裕度的最低點在并網100 臺風機時短暫小于零。由此可見，U與ω比例對穩定性的提升有著很大的幫助。

4 結論

本文針對構網型直驅風電機組接入弱電網場景，建立了系統等值模型，利用阻抗分析法重點分析了電網強度、串補度、風機臺數以及關鍵控制參數對構網型直驅風機并網系統次同步振蕩阻尼的影響。主要結論如下：

1）無串補時，構網型直驅風電機組并網系統在不同電網強度下都不會有SSR 風險。

2）有串補時，構網型直驅風電機組并網系統在電網強度較弱時無諧振風險，在強電網接入條件下SSR 風險增加。

3）隨著構網型直驅風機并網數量的增多，SSR 風險先增大后減小。

4）風速增大會導致SSR 風險增加，直流電壓和輸出轉速的比值增大也會導致SSR 風險增加。