基于多特征融合與優化支持向量機的小電流接地故障區段定位方法

杜政奇，王敬華，張新慧，李晨朝，王洪慶，張 瑩

（1.山東理工大學電氣與電子工程學院，淄博 255049；2.山東科匯電力自動化股份有限公司，淄博 255087）

隨著電力系統規模擴大，各類型故障頻發，故障后需快速檢測出故障位置，隔離故障區段進而恢復供電，但諧振接地系統發生故障時特征信號微弱，給定位造成困難[1]。現有數據表明，電網80%以上的故障均發生在配網側，因配電網作為與用戶直接連接的環節，研究配電網故障定位方法對提高配電網供電可靠性具有重要意義。

現有故障定位技術多以單一特征量為依據來進行故障定位。文獻[2]采用故障點上下游主諧振分量振蕩頻率的差異來實現故障區段定位，但在故障點上下游線路長度一致且高阻接地情況下，故障點上下游零序電流振蕩頻率相似且接近工頻，容易造成誤判。文獻[3]利用廣義S 變換得到暫態零序電流時頻矩陣，以相對熵來衡量故障點上下游的能量差異，對于自動化較低的系統無法滿足同步采樣的要求。文獻[4-5]利用動態時間彎曲距離DTW（dynamic time warping）來描述故障區段兩側的暫態零序電流波形差異，一定程度上解決了采樣不同步的問題，在低阻接地時也具有良好的效果，但在高阻接地時易受線路類型的影響，由于架空線路對地電容遠小于電纜線路，在單相接地故障發生在架空線路區段內時會出現非故障區段穩態零序分量大于故障區段的情況，影響定位可靠性。文獻[6]提取暫態零模電流并構造衰減速度判據，但在高阻接地情況下，暫態高頻分量振蕩頻率接近工頻，在一定情況下需要十幾個工頻周期才會衰減至0，截取的數據窗不易確定。

隨著經驗模態分解EMD（empirical model decomposition）、集合經驗模態分解EEMD（ensemble empirical mode decomposition）、互補集合經驗模態分解CEEMD（complementary ensemble empirical mode decomposition）等信號處理算法的發展，故障特征量的獲取更加便捷，但一些算法本身存在一定缺陷，與理論計算的故障特征量存在偏差。文獻[7]利用EMD自適應分解各出線零序電流，并有效解決了EMD算法本身模態混疊的缺陷，但需要選取故障特征明顯的有效分量。文獻[8-10]采用變分模態分解VMD（variational mode decomposition）算法分解暫態零序電流獲得特征模態分量IMF（intrinsic mode function）時，分解層數K設置為3，但由于故障點下游暫態零序電流第3 個本征模態分量相較于其余高頻信號能量較小，無法準確得到暫態零序電流信號的暫態高頻分量。文獻[11]采用邊界延拓方法對局部均值分解LMD（local mean decomposition）進行改進，消除端點效應和模態混疊問題，并應用于暫態零序電流分解。同時，人工智能的發展為故障定位問題轉化為機器學習中的分類問題提供了新思路。文獻[12]將輕量級梯度提升機LightGBM 應用到故障區段定位中，但由于故障特征量的選取只適用于中性點不接地系統，在經消弧線圈接地系統中容易引起誤判。文獻[13]搭建了基于電壓與數據之間相關性的支持向量機SVM（support vector machine）的故障定位模型，其分類結果準確率不僅與最優特征維數相關，還受SVM算法本身關鍵參數影響。此外，貝葉斯[14]、模糊聚類[15]等分類算法均已被廣泛應用到配電網故障分析中。

傳統故障定位方法多采用閾值整定的方法，故障定位準確度不高。為此，本文在小電流接地系統發生接地故障時，分析研究故障線路各區段暫態零序電流的特征，并在此基礎上提出一種利用自適應VMD構造多種故障特征量和優化SVM融合特征的區段定位新方法。首先利用暫態過程主諧振能量最大原理對VMD 的分解層數K進行自適應優化，然后分解故障暫態零序電流得到1組IMF。從時域和頻域兩個方面分析暫態量蘊含的多種故障信息，構造了5種不同的故障特征量，將高維特征向量輸入到改進鯨魚優化算法IWOA（improved whale optimization algorithm）優化的故障定位SVM分類模型中進行訓練，最后輸出故障區段定位結果。所提方法將區段定位問題轉化為分類問題，提高了故障定位的可靠性。

1 單相接地故障暫態特征分析

為了判定本文所選故障特征量在故障區段定位問題中的有效性，在忽略線路阻抗的前提下，圖1給出了適用于分析健全線路和故障線路各區段暫態零序電流的分布特征。其中，S1為包含全部健全線路的等效故障檢測點；S2、S3為故障點上游區段的相鄰故障檢測點；S4、S5為故障點下游區段的相鄰故障檢測點；iCs為流經全部健全線路的對地電容電流之和；iLp為流經消弧線圈的暫態電感電流；iCu1、iCu2為故障點到母線側各區段內的對地電容電流；iCd1、iCd2為故障點到負荷側各區段的對地電容電流。

圖1 故障零序電流分布Fig.1 Distribution of fault zero-sequence current

由圖1 故障零序電流流向可知，流經故障點的暫態零序電流可表示為

式中：if為流經接地點的暫態零序電流；iup為流經故障點上游的暫態零序電流；idown為流經故障點下游的暫態零序電流。流經故障點上游和下游暫態零序電流表達式分別為

由圖1 可知，故障點上游相鄰檢測點S2和S3零序電流之差為iCu1，故障點下游相鄰檢測點S4和S5零序電流之差iCd1。可見，故障線路上各檢測點暫態零序電流的差異為故障區段定位提供了判定依據。

對于諧振接地系統，故障零序電流分量[15]可表示為

式中：ω0為工頻頻率；；δc為主諧振分量的衰減因子，δc=R2L，其中R和L分別為零模網絡中等值電阻和電感；δL為衰減直流分量的時間常數，δL=RfLp，其中Lp為消弧線圈等值電感，Rf為故障點過渡電阻；ILm=Umω0Lp，ICm=Umω0C，其中Um為系統虛擬電壓源幅值，C為零模網絡中等值電容。

2 VMD 及最優參數選取

2.1 變分模態分解

當配電網發生單相接地故障時，故障線路上的零序電流會發生突變，由饋線終端采集的零序電流信號中存在類似于IMF 的調幅-調頻信號。為了驗證采用VMD[16]分析暫態零序電流信號的可行性，根據式（4）可構造1組仿真信號，即

式中：x1(t)為衰減直流分量；x2(t)為穩態工頻分量；x3(t)為暫態主頻分量。

由式（5）可知，該仿真信號主要包含0 Hz、50 Hz和500 Hz 這3 個頻率成分。VMD 算法預先設置的參數主要有分解層數K、懲罰因子α、凸函數優化相關參數、中心頻率初始化參數、中心頻率更新時的相關參數。

采用VMD對信號x( )t進行分解，設置分解層數K=3，懲罰因子α=20 000，分解結果如圖2所示。

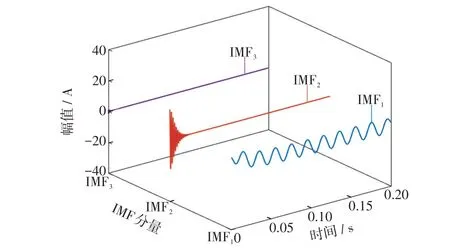
圖2 仿真信號的VMD（K=3）Fig.2 VMD of simulation signal（K=3）

由圖2 可知，當信號中存在衰減直流分量時，設置K= 3 并不能很好地分解仿真信號，x1(t)和x2(t)被分解到同一模態分量(IMF1)中且出現了虛假分量IMF3。為了準確分解暫態零序電流中的衰減直流分量，將IMF1經VMD二次分解，分解結果如圖3所示。

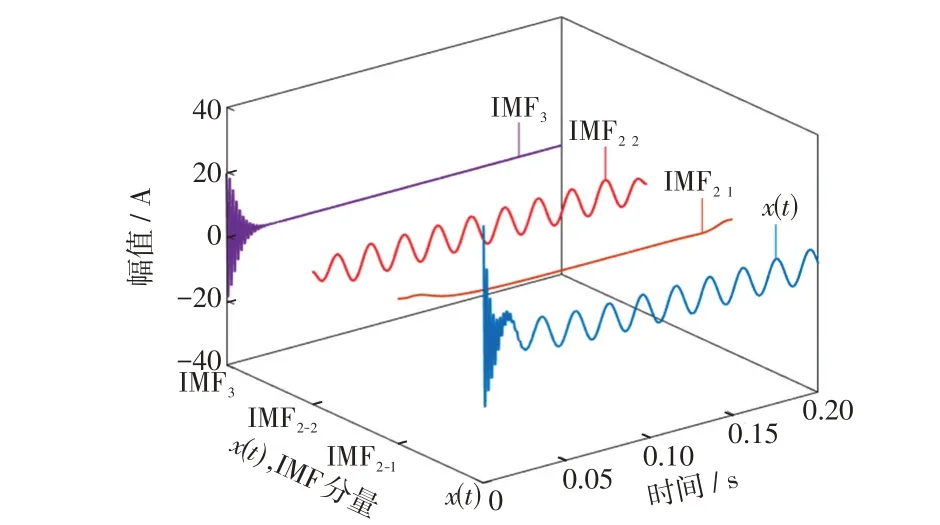
圖3 原始信號及最終分解效果Fig.3 Original signal and final decomposition renderings

圖3中，x(t)為原始信號；IMF2-1為二次分解得到的衰減直流分量；IMF2-2為二次分解得到的穩態工頻分量；IMF3為暫態主頻分量，與原始信號組成的分量一致。

2.2 最優模態參數選取

VMD算法中除分解層數和懲罰因子之外，其他參數對分解效果的影響并不明顯，通常設置為經驗值。分解層K對VMD 的分解效果影響較大，參數K選取合適是取得良好分解效果的關鍵，因此本文只討論參數K的選取。

諧振接地系統發生單相接地故障時，其暫態過程包含了由模網絡相互作用引起的多個串并聯諧振過程。圖4 為一次故障中暫態零序電流在高頻段的幅頻特性。

圖4 暫態零序電流高頻段幅頻特性Fig.4 Amplitude-frequency characteristic of transient zero-sequence current at high frequency

由圖4 可知，主諧振頻率接近1 kHz 且遠大于其他諧振頻率下的能量，與故障瞬間較大的沖擊能量相對應。因此，本文以暫態過程中主諧振分量能量最大原理來優化參數K。根據第6.1節仿真模型所獲得的故障零序電流對VMD關鍵參數尋優過程進行具體分析。K取不同值時，對故障零序電流信號進行VMD，各IMF分量如圖5所示。

圖5 不同K 值下故障零序電流分解Fig.5 Decomposition of fault zero-sequence current under different values of K

由圖5（a）可知，當K=2 時，IMF1為穩態工頻分量與衰減直流分量的疊加，IMF2為暫態主頻分量；隨著K值的增大，分解得到的IMF1和IMF2與K=2時結果相同，但出現了幅值更小的高頻分量。由于各IMF分量為單一頻率信號，故采用快速傅里葉變換來衡量IMF分量的能量大小，結果如圖6所示。

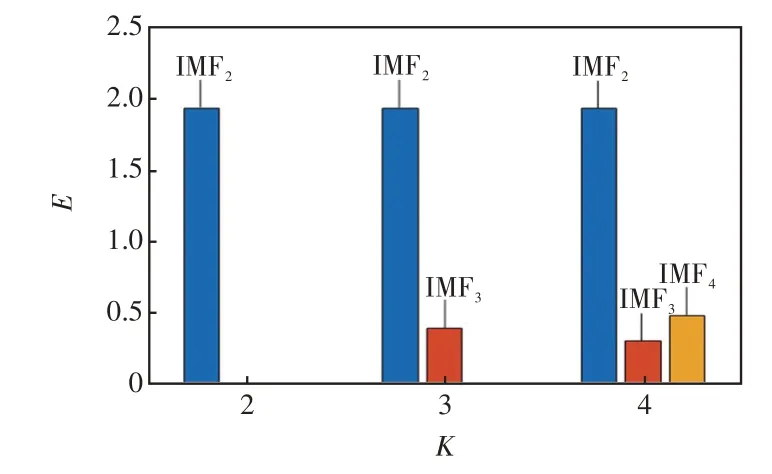
圖6 不同K 值下各IMF 分量能量對比Fig.6 Comparison of IMF component energy under different values of K

從圖6 可以看出，當K=3 時IMF2的能量E大于IMF3且與K=2 時IMF2的能量相同；當K=4時，IMF2仍為能量最大的分量，IMF3和IMF4的能量均遠小于IMF2。綜合以上分析可以得出，最優參數K=2。在最優參數K下，經VMD二次分解可以得到故障零序電流的暫態主頻分量、衰減直流分量和穩態工頻分量。

3 故障特征量的構造

3.1 衰減直流分量衰減速度

為了描述故障線路上不同檢測點故障零序電流中衰減直流分量的差異，定義衰減速度Kup為

式中：|I2-1.up|>|I2-1.down|；I2-1.up為故障點上游區段衰減直流分量；I2-1.down為故障點下游區段衰減直流分量；|I2-1.up|、|I2-1.down|分別為故障點上游、下游區段故障零序電流衰減直流分量的幅值；|I2-1.up|max、|I2-1.up|min分別為故障點上游區段故障零序電流衰減直流分量幅值的最大值和最小值；t1.max、t2.max分別為最大值和最小值對應的時刻。

3.2 暫態主頻分量峰值與穩態工頻分量幅值比

當諧振接地系統發生單相接地故障時，故障點下游健全區段兩端檢測點的暫態主頻分量峰值與穩態工頻分量幅值比嚴格相等[17]。故障點下游、上游的暫態主頻分量峰值與穩態工頻分量幅值的比值分別為

式中：ωl、ωb分別為故障點上游和下游的暫態主諧振頻率；C1為健全線路和故障點上游線路的等值電容；C2為故障點下游線路的等值電容。

故障點上游健全區段由于消弧線圈電感電流對暫態零序電流穩態工頻分量的補償作用，使得故障點上游健全區段相鄰檢測點比值不再相等，且故障區段相鄰檢測點比值更大。基于此差異，可構造故障特征量實現故障區段的準確定位。

3.3 暫態主頻分量與衰減直流分量能量比

為了考慮衰減直流分量在小角度故障時能量占比大的情況，引入暫態主頻分量與衰減直流分量能量比來衡量故障點上下游暫態零序電流在不同故障初相角的能量差異。。

t時刻IMF分量所具有的瞬時能量E(t)為

式中，A(t)為IMF分量在t時刻的瞬時值。

單相接地故障過程的暫態能量函數為

考慮到衰減直流分量與暫態主頻分量的衰減時間不同，本文選取不同的數據窗進行能量計算，衰減直流分量選取5個工頻周期，暫態主頻分量選取1個工頻周期。

3.4 相鄰檢測點故障零序電流波形差異系數

相關系數法忽略了信號幅值對波形相似度的影響。在諧振接地系統中由于消弧線圈的存在，故障線路各區段穩態工頻分量極性相同，均從母線流向線路，如圖1所示。由于故障點上下游線路長度存在較大差別，因此故障點上下游故障零序電流波形存在明顯差異。本文采用DTW衡量各區段故障零序電流波形的差異。DTW的計算公式[18]為

式中：I1、I2為相鄰檢測點的故障零序電流；P為路徑空間，P={p1,p2,…,ps,…,pk} ；元素ps為路徑上第s個點的坐標；k為所有路徑中元素的總數；DTW為距離計算值。

通過1 個積累距離矩陣可求得兩時間序列的DTW(I1,I2)，便于實現。為了消除線路參數對健全區段兩端檢測點故障零序電流的影響，對DTW 進行歸一化處理，即

式中：D*TW為經過歸一化的距離計算值；i1r、i2j分別為時間序列I1、I2的某一瞬時值；m、n為兩時間序列的數據長度。

3.5 相鄰檢測點暫態主頻分量極性比

由于消弧線圈的補償作用，故障線路各區段暫態零序電流中穩態工頻分量的流向一致，均是從母線流向故障點，無法準確判斷故障區段。結合對暫態零序電流的分析，故障點上游各區段零序電流暫態主頻分量幅值較大且初始方向與健全線路、故障點下游線路相反。本文采用差分方法判斷相鄰檢測點故障零序電流暫態主頻分量的初始極性pk,k+1，可表示為

式中：x(n0)為某一點的瞬時值；n0為差分計算的起始采樣點；diff(i)為暫態主頻分量的一階差分測度；sgn(diff(ik))為各檢測點暫態主頻分量一階差分的符號。

4 理論分析

4.1 SVM 基本原理

SVM能提供良好的泛化性能，已被廣泛應用于小樣本分類中[19]。故障定位問題中作為經典的非線性問題，SVM無法在原始樣本空間中找到分類超平面，需引入核函數K( )xi,xj映射到高維空間線性可分。本文采用高斯核函數映射變換，其表達式為

式中：xi、xj為樣本向量；‖xi-xj‖2為xi和xj之間距離的平方；γ為核函數本身的超參數。

引入松弛變量度量訓練集中單個樣本違背約束的程度，得到軟間隔核化SVM的基本型，即

式中：ξi為松弛變量；c為懲罰因子；xi為輸入的第i個樣本；yi為樣本類型；ω為SVM 的自身參數；?(xi)為映射后的樣本向量。

引入拉格朗日懲罰因子α，最終得到軟間隔高斯核SVM的對偶型，即

式中：αi和αj為懲罰參數；γ和c為兩個需要預先設定的超參數。由式（17）可知，SVM模型中超參數γ和c設定值直接決定了SVM 的最終分類效果。當c較大時，分類邊界會傾向于復雜，最大間隔帶的寬度較小，支持向量由較少的樣本組成；當c較小時，支持向量由多個不滿足大間隔約束的樣本組成。超參數γ可以近似認為控制每個支持向量的影響范圍。

4.2 改進鯨魚優化算法

為克服傳統優化算法易陷入局部最優的問題，采用IWOA[20]對SVM的兩個超參數尋優。

為了提高種群的復雜性，在傳統WOA中，引入混沌理論生成初始狀態的種群，其表達式為

同時，在鯨魚位置更新后增加反饋階段，通過交流學習使種群中最差鯨魚能快速運動到食物附近，提高算法的收斂速度，其表達式為

式中：Xwor-new為更新后的位置向量；Xwor為種群中最差鯨魚個體位置向量；Xp為隨機選擇的個體；r為0～1之間的隨機數。

此外，在收縮包圍機制和螺旋更新位置數學模型中引入自適應慣性權重，進一步改善算法的優化性能。

自適應慣性權重w的表達式為

式中：f(x)為適應度函數，本文選取測試集的分類準確率作為適應度函數；u為第1 次迭代種群中的最優值；n1為當前的迭代次數。

最終得到的位置更新公式為

式中：Xp(t)為獵物位置向量；X(t)為當前鯨魚位置向量；A0和C0為系數向量；D0為鯨魚與獵物之間的距離；b為1個常數；l為[-1，1]內的隨機數。

隨著迭代次數增加，適應度值與慣性權重近似成反比，保證了慣性權重的自適應性，很大程度上提高了算法的全局優化能力。

5 區段定位流程

故障區段定位流程如圖7所示，具體步驟如下。

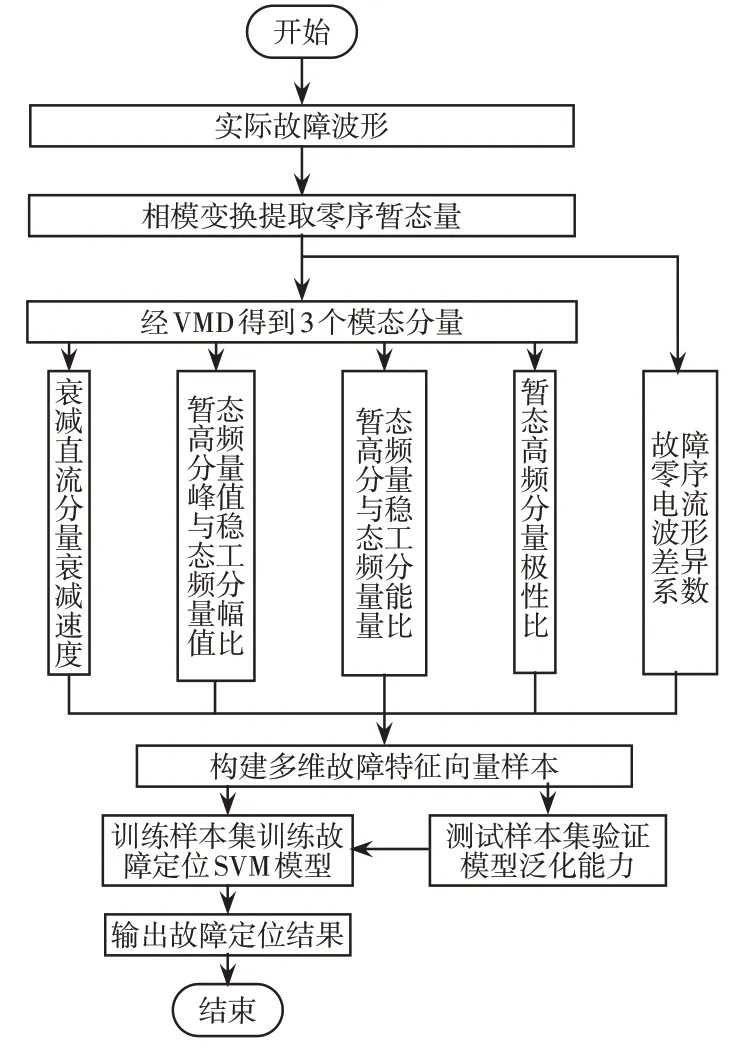
圖7 故障定位流程Fig.7 Flow chart of fault location

步驟1判定發生故障后，利用各檢測點故障指示器提取故障線路各區段的電流波形，采樣時間為0.1 s，采樣頻率為10 kHz，

步驟2采用自適應VMD暫態零序電流，獲得多組IMF分量。

步驟3結合時域波形及頻域分解得到各模態分量，構建5個特征量。

步驟4計算各區段的多維特征量，構建用于SVM分類模型的輸入特征向量。

步驟5改變故障初相角、過渡電阻等故障條件，獲得多組故障樣本，按照高阻和低阻接地的發生概率比劃分訓練集和測試集，驗證故障區段定位效果。

6 仿真分析

6.1 模型搭建

在ATP/EMTP 中搭建10 kV小電流接地系統仿真模型[21]，如圖8 所示。設消弧線圈脫諧度為8%，計算可得Lp=0.25 H；消弧線圈本身阻值為感抗的2%，RL=1.57 Ω。線路參數如表1所示。

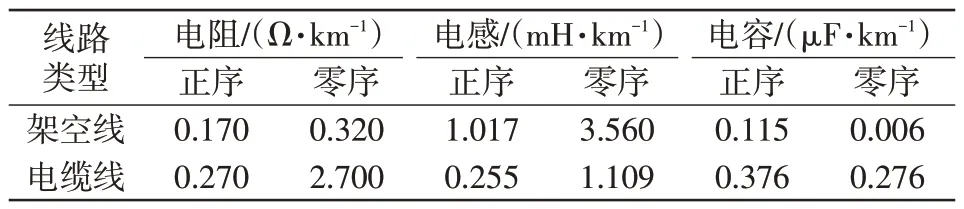
表1 線路阻抗參數Tab.1 Line impedance parameters

圖8 諧振圈接地系統仿真模型Fig.8 Simulation model of resonant coil grounding system

模擬不同過渡電阻、故障初相角和故障位置下單相接地故障時的故障零序電流，提取故障特征，獲得300組故障樣本。按照7∶3的比例劃分訓練集和測試集，為了符合實際情況下低阻與高阻接地發生概率不同的情況，在210組訓練樣本中設置低阻接地故障樣本為150 組、高阻接地故障樣本為50組、另外10組樣本隨機選取的方式。以區段編號作為分類目標，區段1為第1種分類結果，區段2為第2種分類結果，以此類推，區段5為第5種分類結果。

6.2 SVM 參數尋優

分別采用WOA和IWOA對SVM的兩個超參數γ和c進行優化，設置種群個數為20，最大迭代次數為100，γ∈[0.01,10] ，c∈[0.1,100] 。兩種算法的適應度迭代曲線如圖9所示。表2給出了兩種算法性能對比結果。可以看出，IWOA 的運行時間比WOA少1.39 s，最佳適應度迭代次數兩種算法相差不大，但IWOA 的平均適應度收斂速度明顯快于WOA。經IWOA-SVM模型訓練10次后得到的平均最優值為c=3.669 3、γ=1.148 7，此參數下訓練模型分類準確率為98.89%；經WOA-SVM模型訓練10次得到的平均最優值為c=12.256 9、γ=0.653 4，此參數下訓練模型的分類準確率為96.67%。

表2 兩種算法性能對比Tab.2 Comparison of performance between two methods

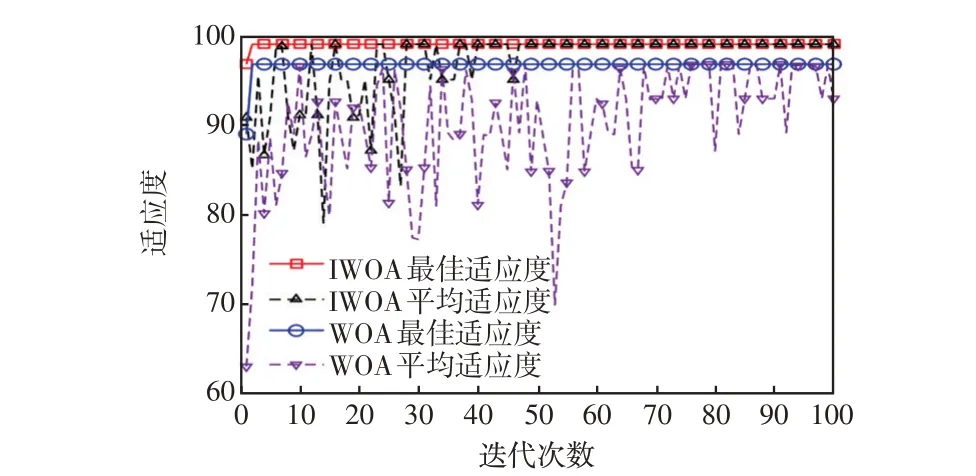
圖9 兩種SVM 參數尋優算法的適應度迭代曲線Fig.9 Fitness iteration curves of two SVM parameter optimization algorithms

6.2 結果分析

在最優參數c和γ下得到IWOA-SVM 故障定位分類模型，測試集分類準確率達到98.89%，測試集分類結果如圖10所示。

圖10 測試集分類結果Fig.10 Classification results of test set

在故障線路末端靠近負荷側發生高阻接地故障時，由于故障初相角為90°時衰減直流分量較小，加之上游檢測點采集的暫態零序電流幅值較小且含噪聲造成特征不明顯，從而出現誤選問題。不同特征向量分類準確率對比如圖11 所示。可以看出，特征1～5的定位正確率依次為84.44%、87.78%、92.22%、94.44%、95.56%，相比于特征融合的SVM分類模型定位正確率分別降低了14.45%、11.11%、6.67%、4.45%、3.33%。

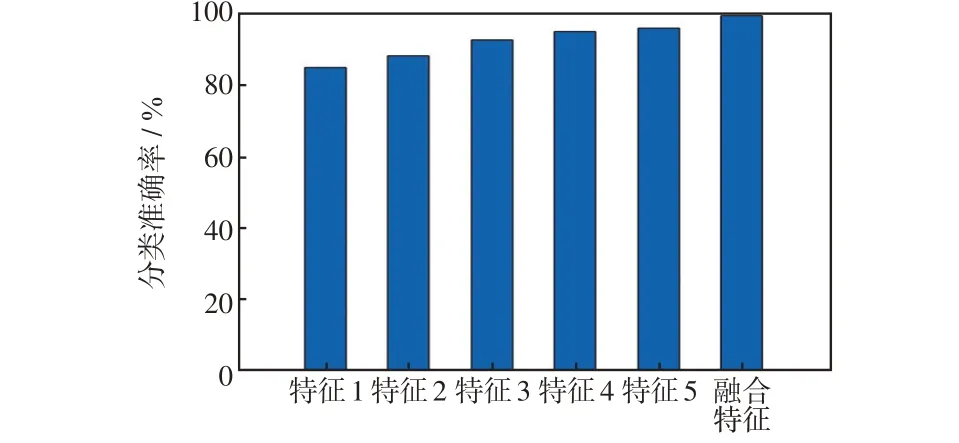
圖11 不同特征向量分類準確率對比Fig.11 Comparison of classification accuracy among different feature vectors

7 結 論

本文以暫態過程中故障信息為依據，結合SVM提出了一種多特征融合的單相接地故障區段檢測方法。主要結論如下。

（1）基于暫態零序電流在故障線路各區段的差異，構造了5 個特征量用于故障定位，即衰減直流分量衰減速度、暫態主頻分量峰值與穩態工頻分量幅值比、暫態主頻分量與衰減直流分量能量比、相鄰檢測點故障零序電流波形差異系數、相鄰檢測點暫態主頻分量極性比。

（2）采用IWOA 優化SVM 的關鍵參數，融合多個時頻特征量構成高維特征向量，得到用于故障定位的分類模型。

（3）通過仿真分析驗證了本文所提定位方法在不同故障條件下的適用性。所提方法的故障定位正確率相比于利用不同單一特征量的定位方法均有不同程度的提高，且在小初相角、高阻接地等極限故障情況下能準確定位故障區段，可靠性高。

由于VMD的分解效果受1個關鍵參數（即懲罰因子α）的影響較大，適用于暫態零序電流分解的最優值有待研究。同時，實際配電網中還存在電弧接地等情況，本文所提方法的適用性還需進一步驗證。