以UPFC 為邊界的新型線路距離保護方法

董政鑫，李 斌，胡澤鵬，鄭玉平，吳通華，孫天甲

（1.智能電網教育部重點實驗室（天津大學），天津 300072；2.國網天津市電力公司濱海供電分公司，天津 300450；3.南瑞集團有限公司（國網電力科學研究院有限公司），南京 211106；4.國網上海市電力公司，上海 200122）

隨著電網規模的逐漸擴大，電網結構也日益復雜[1-2]，存在多種類型運行方式，電網的安全穩定性受到了較大的挑戰，電網運行過程中對潮流控制能力的要求進一步提高[3]。電力系統傳統機械控制方式與新建線路等調節線路潮流的成本較高，而柔性交流輸電系統FACTS（flexible alternative current transmission system）具有突出的技術優勢[4]，逐漸成為增強電網潮流控制水平的重要方法[5]。統一潮流控制器UPFC（unified power flow controller）可以實現對電力系統有功和無功功率的有效調節，近年來逐漸得到很好的工程應用。當電力系統發生故障時，由于UPFC的接入影響了故障電流、電壓等故障暫態特征，可能導致保護誤動作，給線路保護帶來了技術挑戰。

文獻[6]建立了UPFC的詳細模型并將其接入交流線路中，通過仿真分析了不同故障類型下UPFC接入對線路距離保護的影響。文獻[7]通過分析UPFC 接入線路的典型故障特性，指出了傳統差動保護的不足，提出了一種改進的串聯變壓器差動保護方法。文獻[8]分析了UPFC接入線路在正向和反向故障時的工頻變化量阻抗，指出了正向故障時方向保護可以正確動作、反向故障時方向保護可能誤動作，提出了通過電壓變化量補償系數來判斷工頻變化量方向保護動作行為。文獻[9]基于南京西環網UPFC 示范工程，通過理論分析和仿真計算研究了UPFC 接入對線路縱聯保護的影響。文獻[10]分析了系統振蕩時不同控制參數下UPFC對所接入線路測量阻抗的影響，研究發現UPFC 的接入加快了阻抗軌跡的運動速度。

UPFC接入線路的保護方法已有相關研究。為解決UPFC給線路保護帶來的影響，文獻[11]提出了一種UPFC 接入線路的自適應接地距離保護方法，該方法在UPFC的多種控制參數下均適用；文獻[12]通過采用小波能量熵提取母線各出線暫態信息，提出了一種適用于含UPFC 線路的方向縱聯保護方案；文獻[13]提出了一種基于小波多分辨率分解的故障定位方法，該方法可以不受UPFC 接入的影響對線路的故障位置進行準確定位；文獻[14]提出了一種基于波形相似度比較的線路縱聯保護方案，利用故障后線路兩端波形信號不一致的特點判別故障位置；文獻[15-16]基于輸電線路阻感模型提出了一種以串補電容為線路邊界的新型距離保護方法，并引入誤差權重矩陣減小算法誤差；文獻[17]利用神經網絡算法自適應地調整UPFC接入后線路保護故障動作邊界；文獻[18]利用區內外故障時線路兩端暫態電流的波形差異，提出了一種基于余弦相似度的縱聯保護方法。

綜上所述，本文針對UPFC 接入交流線路后線路阻抗均勻性不再連續而引起傳統距離保護可能誤動作的問題，提出一種基于最小二乘的以UPFC為線路邊界的單端量保護方法。基于輸電線路阻感模型，對含有UPFC 的輸電線路進行故障暫態分析，推導故障距離和擬合誤差的時域表達式，根據故障發生時的故障距離和擬合誤差來判別故障位置。通過仿真驗證所提保護方案可以有效判別以UPFC 為線路邊界的區內外故障，可適用于多種類型故障，具有較強的適用性。

1 UPFC 工作原理及其對測量阻抗的影響

UPFC是由兩個模塊化多電平換流器構成串并聯的結構，其中并聯換流器與串聯換流器直流側通過電容相連，構成功率流通的通道，交流側通過變壓器與交流系統相連。拓撲結構及線路故障位置如圖1所示，其中為母線電壓，為UPFC接入后的線路受端電壓，f1為線路故障位置，f2為線路送端母線故障位置，為UPFC串聯側注入補償電壓，為UPFC并聯側等效注入電流，為UPFC串聯側所在線路電流，Z1和Z2為交流線路故障時故障點f1兩側的線路阻抗。

UPFC 串聯側的功能可以用1 個位于串聯線路上的可控電壓源來代替，隨著UPFC 控制參數的變化，電壓源的幅值及相角隨之變化，當需要實現不同控制目標時，通過改變控制參數來調節注入的電壓矢量。由于串聯側注入電壓與線路電壓存在相位差，因此會發生功率交換。串聯側換流器所需的有功功率通過直流電容從并聯側獲得，整個裝置對外保持有功功率平衡。并聯側換流器除去維持功率平衡的作用外，并聯側換流器還可以自主產生無功功率對并聯接入點進行無功補償，維持節點電壓穩定。

根據UPFC串聯側電壓幅值及相角的不同，UPFC可實現電壓調節、相角調節、阻抗補償及綜合調節4種功能，如圖2所示，其中為UPFC接入系統點電壓。

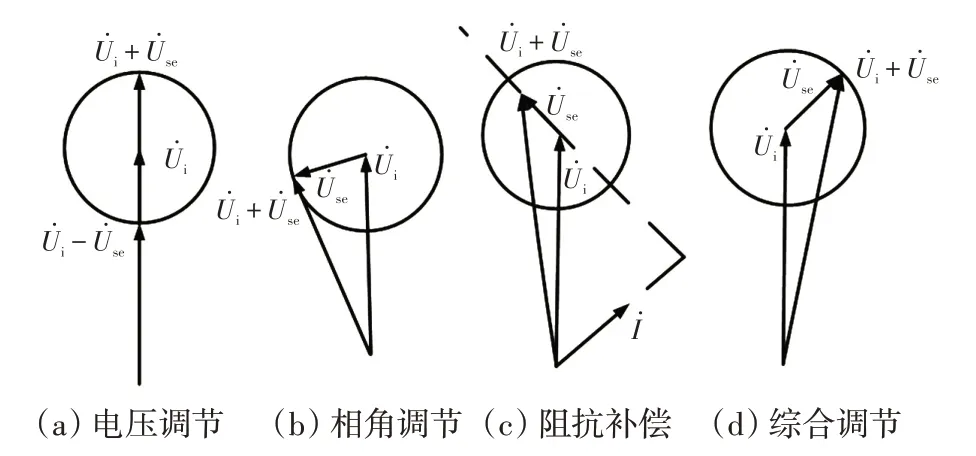
圖2 UPFC 的多種功能Fig.2 Multiple functions of UPFC

通過對UPFC 工作原理分析，假設故障時串聯側及并聯側設備均不被旁路。

圖1中保護1測量UPFC所在母線上的電壓、電流等電氣量，保護2 測量UPFC 所在線路對端的電氣量。通過分析故障發生在不同位置處時對保護1和保護2的影響來研究UPFC接入對線路距離保護的影響。

（1）當故障發生在線路上f1處時，故障點與保護1之間包含UPFC的串聯側，由于此時UPFC不被旁路，則保護1 的測量阻抗ZJ1受到串聯側注入電壓的影響，其表達式為

對端保護2 與故障點之間不包含UPFC，因此測量阻抗不受影響，保護可以正確動作。

（2）當故障發生在UPFC所在母線上f2處時，故障點與保護1 之間不包含UPFC 設備，因此測量阻抗不受影響。

對端保護2 與故障點之間包含UPFC 的串聯側，由于此時UPFC不被旁路，則保護2的測量阻抗ZJ2的表達式為

綜上所述，如果故障時UPFC未被旁路，當故障點和保護安裝處之間包含UPFC 設備時，原有的線路阻抗均勻性被破壞，距離保護元件計算得到的測量阻抗會受到UPFC 接入的影響，傳統的距離保護可能發生誤動。

2 以UPFC 為邊界的線路距離保護

2.1 含有UPFC 的輸電線路故障電流暫態分析

以圖3所示的UPFC接入輸電線路阻感模型進行說明，其中線路保護安裝于母線N端，uM、iM分別為故障時M 端的電壓、電流瞬時值，uN、iN分別為故障時N 端的電壓、電流瞬時值，Lline為被保護線路全長，x為故障點f1與N端之間的距離，r、l分別為保護安裝處至故障點的線路單位長度等效電阻與電感，ZM、ZN為系統阻抗。

圖3 含UPFC 的輸電線路阻感模型Fig.3 Transmission line resistance-inductance model with UPFC

N端保護安裝處采集到的電壓瞬時值uN為

式中：Un為系統電壓幅值；ω為工頻角速度，在交流頻率為50 Hz 下ω=100π rad/s；α為N 端系統電壓的初相角。

當線路f1處發生故障時，可以得到N端保護安裝處的電壓、電流關系應滿足

式中，i為UPFC所在線路電流。

故障電流的解析式為

當故障點位于UPFC之后母線f2處時，UPFC串聯側注入的電壓use為

式中，β為串聯側注入電壓與N端系統電壓的初始相角差。

此時N端系統等效電壓ueq和故障電流的解析式分別為

由式（8）可知，UPFC 接入線路后，故障電流中工頻穩態分量和衰減暫態分量幅值均受到UPFC串聯注入電壓的影響，且由于UPFC 串聯注入電壓在故障時變化狀態較為復雜，此時如果利用保護安裝處采集到的電壓與故障電流計算測量阻抗，傳統距離保護可能發生誤動。

2.2 基于輸電線路阻感模型進行故障定位

如圖3所示，N端保護發生區內故障時，例如線路f1處發生A 相金屬性單相接地故障，N 端保護安裝處獲取的電壓、電流的關系應滿足

式中：iNA為N端保護安裝處A相電流；i0為故障發生時零序電流；r1、l1分別為線路單位長度的正序電阻和正序電感；r0、l0分別為線路單位長度的零序電阻和零序電感；k1、k2分別為故障發生時電阻和電感的零序補償系數，k1=(r0-r1) /3r1，k2=(l0-l1) /3l1。由于電壓、電流的采樣值是離散數據，采用中值差分代替微分的方法，可以將式（9）改寫為

式中：n為采樣序列編號；Δt為采樣時間間隔。

線路運行過程中，N 端的保護裝置不斷采集電壓、電流數據，利用1 個數據窗內的采樣值形成一系列滿足式（10）的方程，用矩陣形式可表示為

其中

式中：U為電壓采樣數據按時間順序排列形成的矩陣；w為電流采樣值與單位長度電阻、電感值乘積形成的按時間順序排列矩陣；L為待求系數矩陣；n為采樣序列編號；k為單個數據窗包含采樣點數量；Δt為采樣時間間隔；uNi為N 端保護安裝處采樣電壓值。

對式（11）采用最小二乘法求解矩陣L，使得數據窗內電壓計算值與實際值差距最小，定義該差距為擬合誤差E，即

式中，‖ ‖2表示L2范數。擬合誤差E根據系統N端電壓取標幺值，其取值范圍為[0，1]。

當擬合誤差對矩陣L求偏導數為0 時，可使得數據窗內電壓計算值與實際值差距最小，由此可得

當采樣頻率較高時，可以通過忽略離散誤差得到故障距離和擬合誤差的時域解析式分別為

式中：t0為當前時間窗開始采樣時的采樣時刻；t為當前時間窗結束采樣時的采樣時刻；T1為所用時間窗的長度，T1=t-t0。

當故障點與保護N 之間不包括UPFC 時，將式（3）和式（5）代入式（17）和式（18）可以計算得到故障距離和相應的擬合誤差分別為

當故障點與保護N之間包括UPFC時，將式（7）和式（8）代入式（17）和式（18），可以計算得到故障距離和相應的擬合誤差分別為

式中：T2為采樣總時長；其他參數表達式見附錄A。

2.3 以UPFC 為邊界的線路距離保護方法及判據

根據上述UPFC接入線路后故障電流分析及對最小二乘法求解微分方程組的原理介紹，可以得到故障距離及擬合誤差是判斷以UPFC為線路邊界的區內外故障的關鍵指標和判別依據。圖4為以UPFC為線路邊界的單端量保護方法具體實現方案及故障判據。

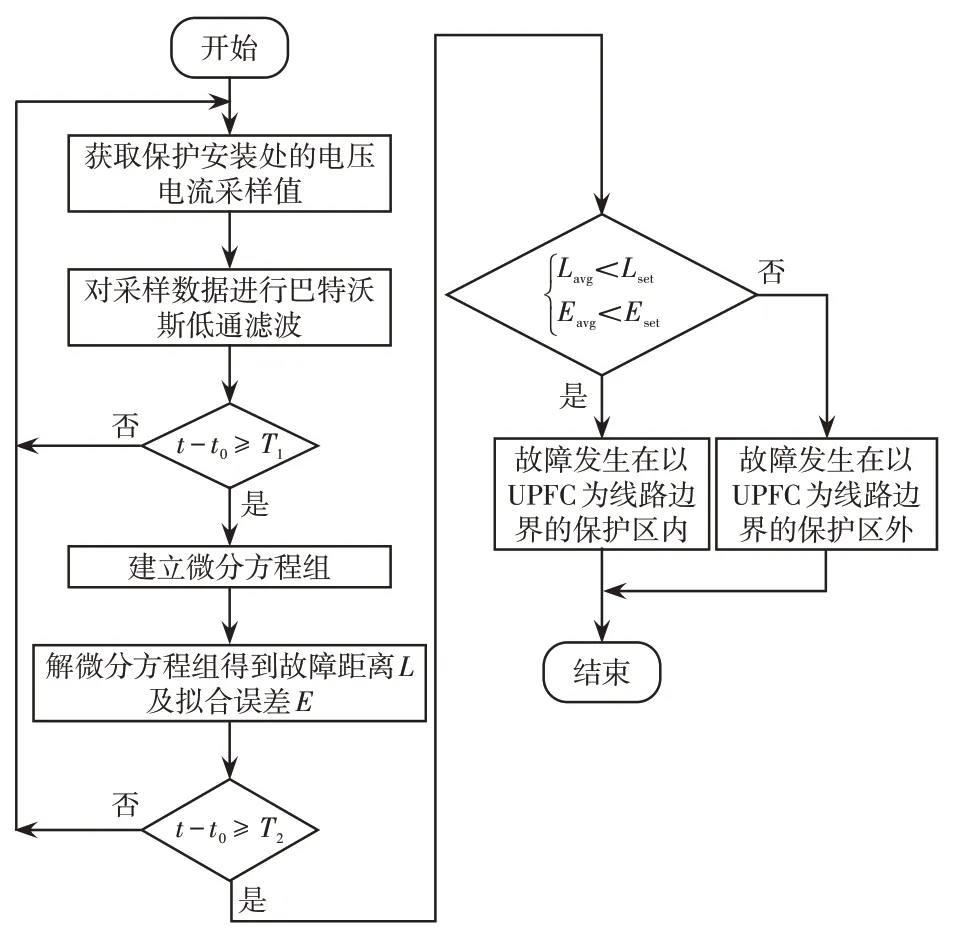
圖4 以UPFC 為邊界線路距離保護方案流程Fig.4 Flow chart of distance protection scheme with UPFC as line boundary

首先獲取當前線路運行過程中線路N 端保護裝置采集的電壓和電流數據(uN、iN)。為了避免高次諧波可能對算法帶來較大的干擾，采用巴特沃斯低通濾波器對獲得的電壓、電流數據進行低通濾波。設t為當前采樣時刻；t0為故障發生時刻；T1為采樣數據窗長，本文取10 ms；T2為采樣總時長，本文取40 ms。若t-t0≥T1，則利用數據窗內獲得的采樣值建立微分方程組，否則繼續采樣。利用最小二乘法對微分方程組進行求解，求得每個數據窗內采樣序列的故障距離及擬合誤差。若t-t0≥T2，則停止采樣，進行故障位置判別，否則移動到下一個采樣點繼續采樣。通過移動數據窗重復求解出多組解L和E，根據故障距離及擬合誤差隨時間變化的曲線，進行故障判別。

由大量仿真可知，計算結果在故障發生后大約10 ms 開始穩定，通常故障發生40 ms 后UPFC 通過旁路裝置從線路中切除，因此取故障發生后10～40 ms之間的計算結果。保護判據為

式中：Lavg為故障發生10～40 ms期間故障距離計算值的平均值；Lset為故障距離整定值，本文取線路全長100 km；Eavg為故障發生10～40 ms 期間擬合誤差E的平均值；Eset為擬合誤差整定值，本文取0.015。

綜上所述，若滿足保護判據，則計算使用的輸電線路阻感模型與實際故障情況相符，故障發生在N 端保護以UPFC 為線路邊界的保護區內，否則故障發生在以UPFC為線路邊界的保護區外。

3 仿真驗證

3.1 仿真模型

在PSCAD/EMTDC 平臺上搭建如圖1 所示的UPFC 接入220 kV 輸電系統的仿真模型。UPFC 主要參數如表1所示。輸電線路長度為100 km，單位長度線路線路正序阻抗為（0.034 3+j0.418 8）Ω/km，單位長度線路零序阻抗為（0.291 3+j1.156 6）Ω/km。所提保護安裝在N側母線處，選用三階巴特沃斯濾波器對采集到的電壓、電流電氣量進行低通濾波，截止頻率為120 Hz，采樣頻率取10 kHz，最小二乘法的數據窗長選取為1 ms。仿真總時長設置為2 s，故障發生在t=1.0 s，假設故障時晶閘管旁路開關及串聯側高壓旁路開關不導通。

表1 UPFC 模型系統參數Tab.1 System parameters of UPFC model

3.2 區內故障

如圖3 所示，以N 側母線處的距離保護為分析對象，在線路上f1處發生的故障是距離Ⅰ段的區內故障。

在區內故障情況下，分別在線路上距離母線N線路長度50%（即距離母線N線路長度50 km處）的f1處設置A相金屬性接地短路故障。

線路長度50%處發生A 相金屬性接地故障如圖5 所示。可以看出，當f1處發生A 相金屬性接地短路故障時，基于最小二乘的以UPFC 為線路邊界的單端量保護方法故障距離計算值在故障發生10 ms 后開始逐漸收斂，故障發生后10～40 ms 期間故障距離平均值為50.05 km，小于被保護線路全長，符合實際情況，且擬合誤差平均值為5.36×10-5，小于整定值，滿足判據（見式（23））。上述結果表明，故障發生在N端保護以UPFC為線路邊界的保護區內，與實際情況相符。在保護區內不同位置發生不同故障類型時的擬合誤差及故障測距結果如表2所示，其中AG表示A相單相接地故障，AB表示AB相間短路，ABG表示AB相間接地短路，ABC表示三相短路。可以看出，區內不同位置發生不同類型故障時所提保護方法均能有效判定故障位置，且隨著過渡電阻的增大誤差逐漸增大。

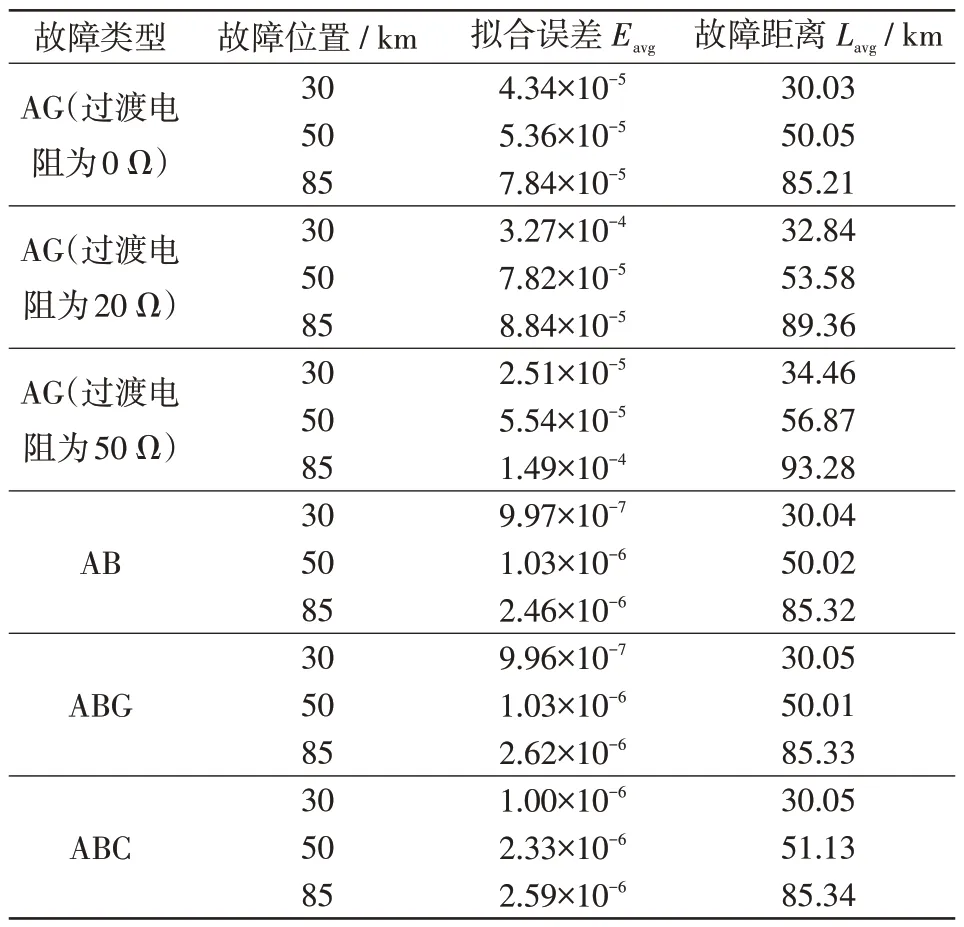
表2 保護區內發生故障時的計算結果Tab.2 Calculation results under fault in the protection zone

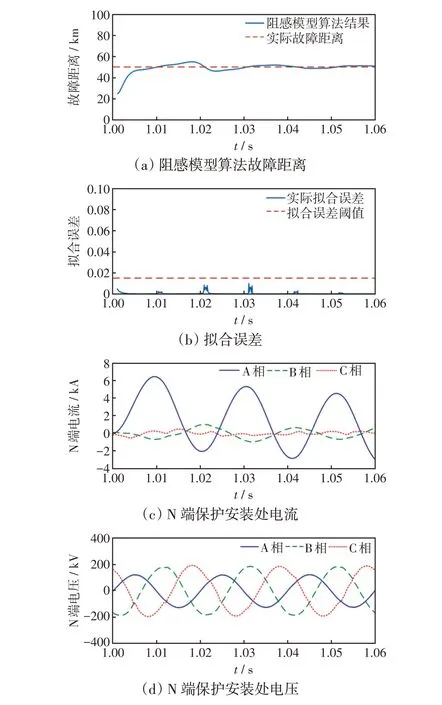
圖5 線路長度50%處發生A 相金屬性接地故障Fig.5 Phase-A metallic grounding fault occurring at 50% of line length

3.3 區外故障

如圖3 所示，以N 側母線處的距離保護為分析對象，在母線M上f2處發生的故障是距離Ⅰ段的區外故障。

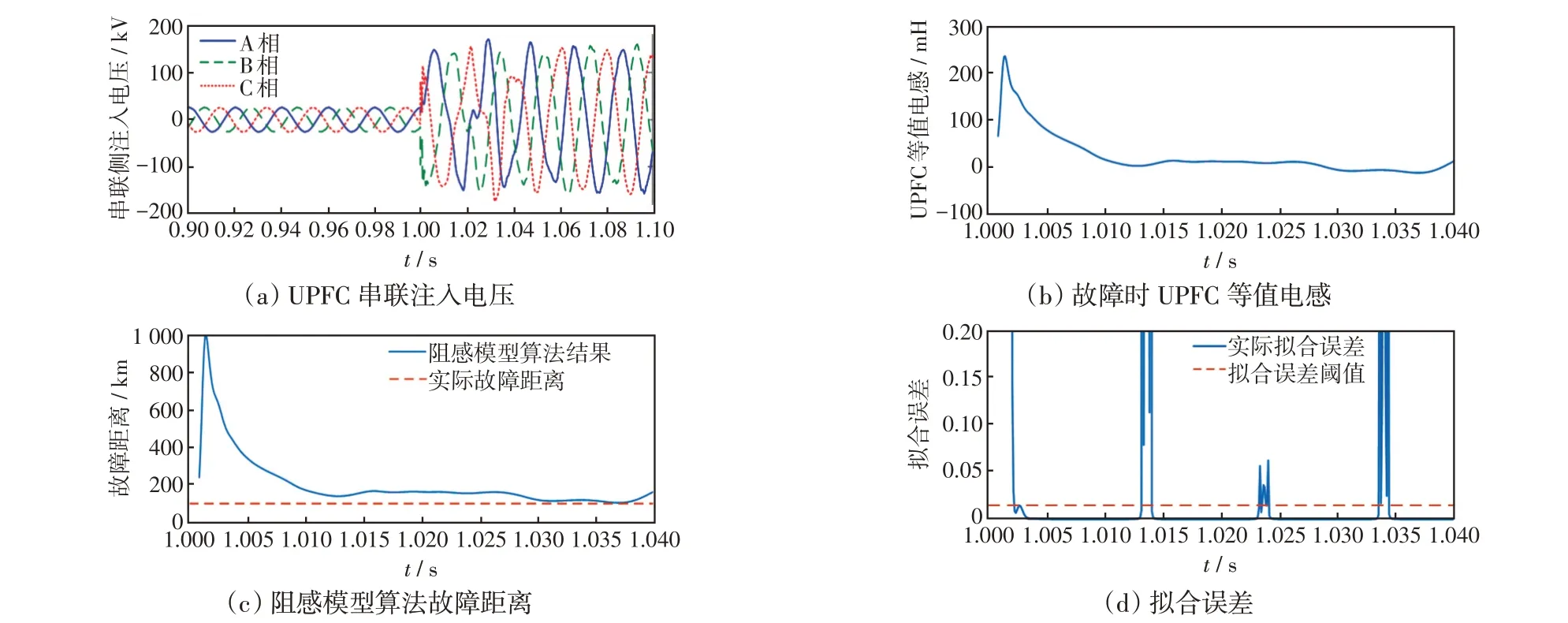
假設f2處發生A 相金屬性接地短路故障，N 側母線處距離保護所得到的故障距離、擬合誤差、UPFC 串聯注入電壓及UPFC 串聯接入產生的等值電感如圖6 所示。可以看出，當發生A 相金屬性接地短路故障時，基于最小二乘的以UPFC 為線路邊界的單端量保護方法故障距離計算值在故障后發生較大波動，不能收斂，且在故障后10～40 ms 期間故障距離平均值為240 km，超過被保護線路全長，擬合誤差的平均值大于設定的門檻值，不滿足判據（見式（23））。上述結果表明，故障發生在N端保護以UPFC為線路邊界的保護區外，與實際情況相符。

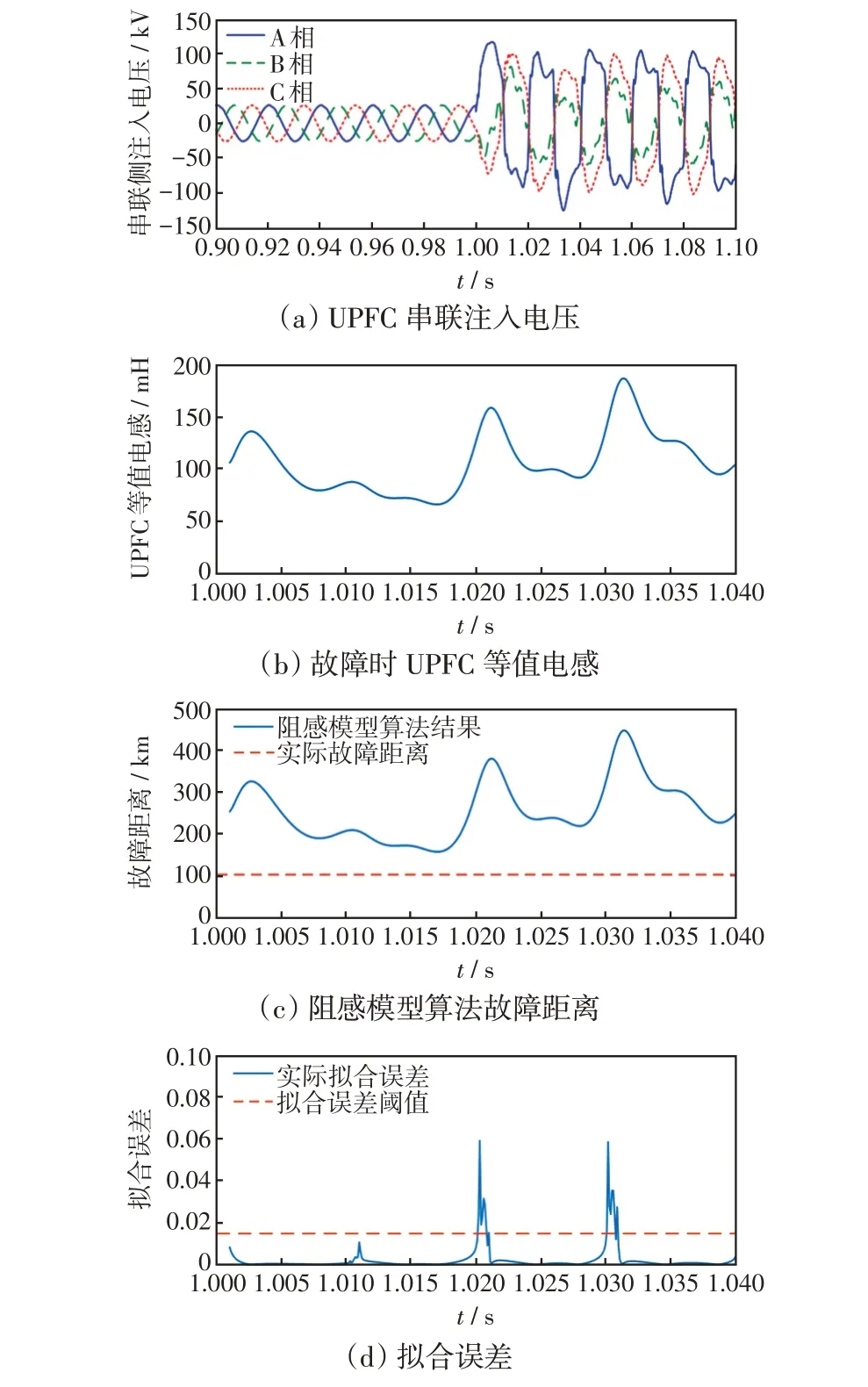
圖6 f2處發生A 相金屬性接地故障Fig.6 Phase-A metallic grounding fault occurring at point f2

4 結 語

UPFC接入輸電線路后對傳統距離保護有很大影響，本文對含有UPFC 的輸電線路進行了故障暫態分析，推導了故障距離與擬合誤差的時域表達式。在此基礎上，提出了一種基于最小二乘的以UPFC 為線路邊界的線路距離保護方法，進而給出了這種方法的具體算法及流程。所提方法將采集到的電壓、電流數據經過低通濾波，然后根據阻感模型建立微分方程組，使用最小二乘法進行求解得到相應的故障距離和擬合誤差。仿真結果表明，當發生區內故障時，計算得到的故障距離可以快速收斂至真實值且擬合誤差較小；當發生區外故障時，故障距離計算值大于線路全長且擬合誤差較大。因此，依據故障距離計算值及擬合誤差可以有效判斷故障點和UPFC的相對位置關系。理論分析及仿真結果表明，該方法適用于多種故障類型，具有較好的實用性。

附錄A 部分參數表達式

附錄B 線路長度50%處發生不同類型故障時的仿真結果

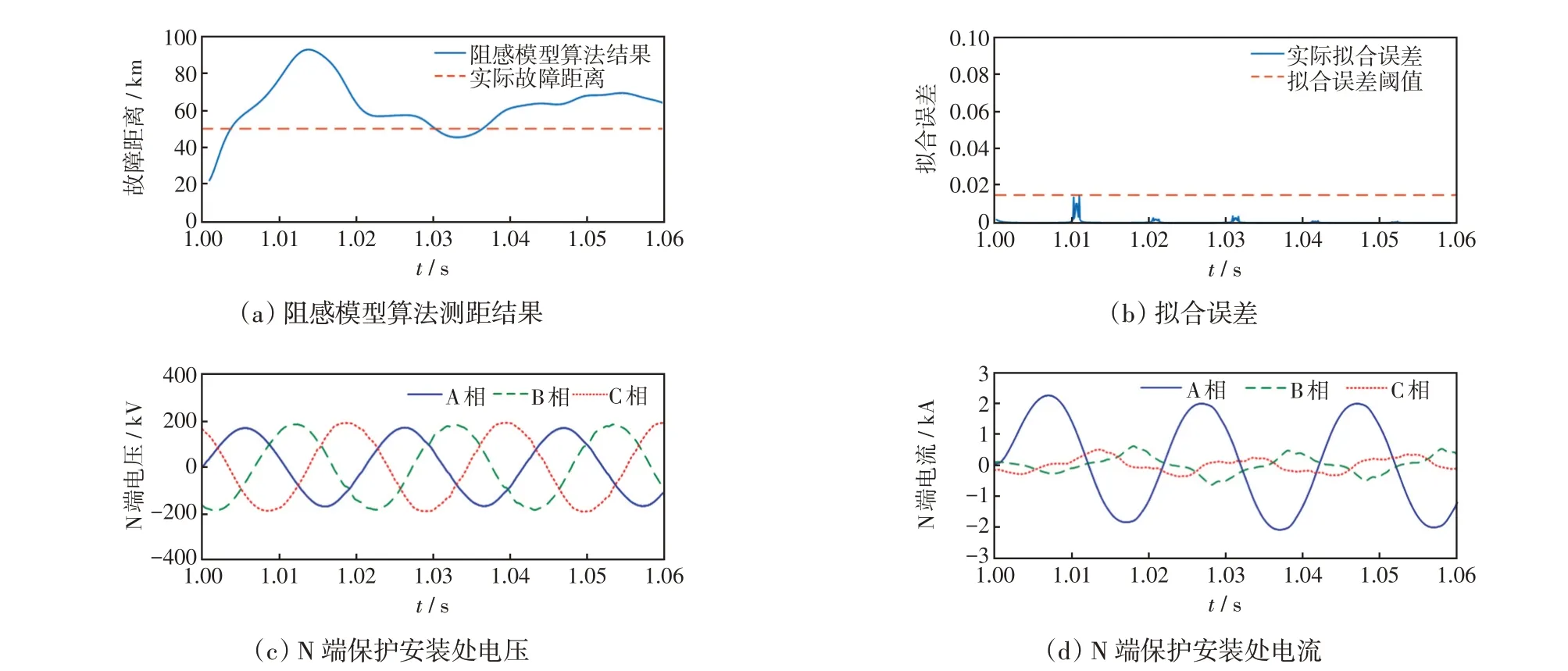
附圖B-1 線路長度50%處發生A 相經50 Ω 過渡電阻單相接地故障Fig.B-1 Phase-A single-phase grounding fault through 50 Ω transition resistance occurring at 50% of line length

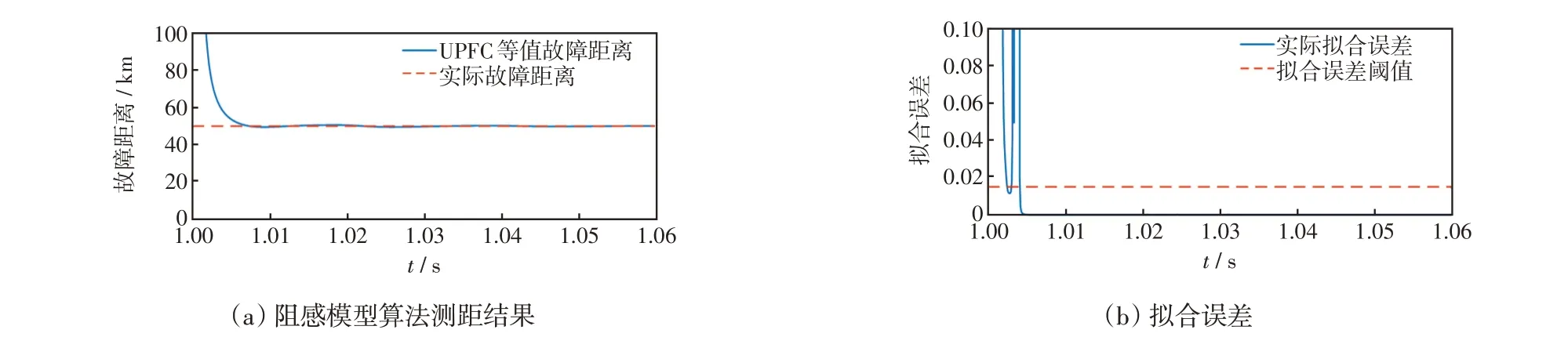
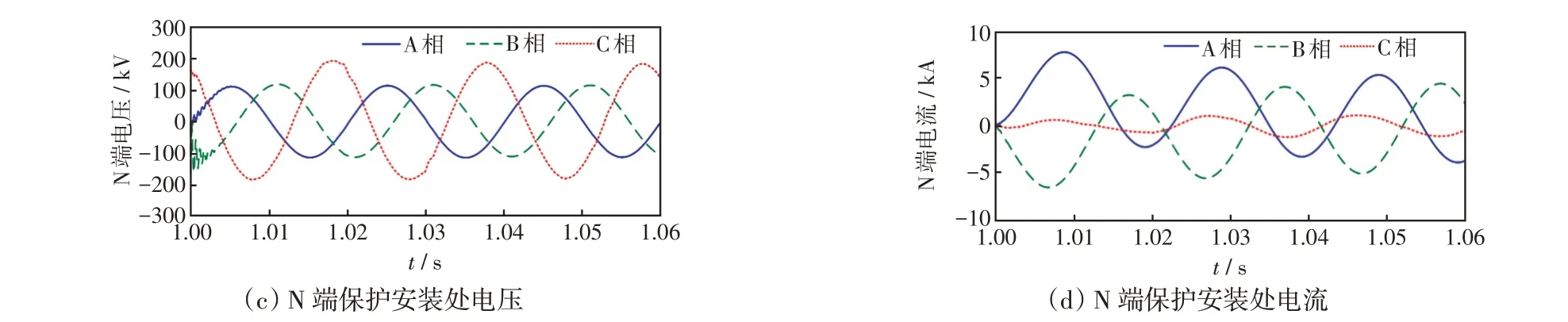
附圖B-2 線路長度50%處發生AB 相間短路故障Fig.B-2 Phase A-to-phase B short-circuit fault occurring at 50% of line length

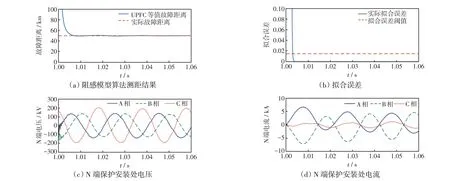
附圖B-3 線路長度50%處發生AB 相間接地短路故障Fig.B-3 Phase AB-to-ground short-circuit fault occurring at 50% of line length

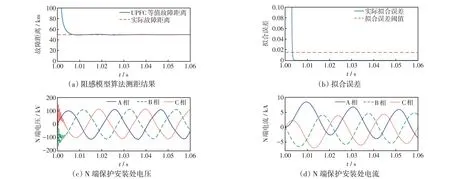
附圖B-4 線路長度50%處發生三相故障Fig.B-4 Three-phase fault occurring at 50% of line length

附錄C 保護區外發生不同類型故障時的仿真結果

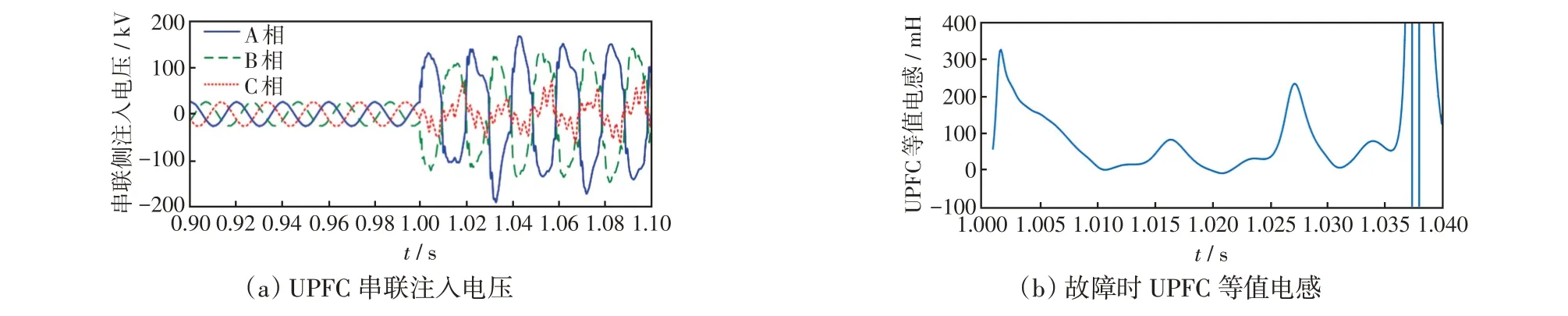
附圖C-1 f2點處發生AB 相間短路故障Fig.C-1 Phase A-to-phase B short-circuit fault occurring at point f2

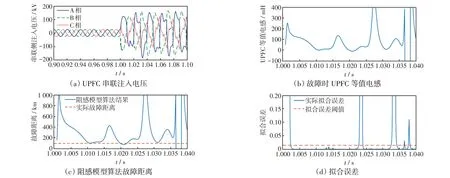
附圖C-2 f2點處發生AB 相間接地短路故障Fig.C-2 Phase AB-to-ground short-circuit fault occurring at point f2

附圖C-3 f2點處發生三相短路故障Fig.C-3 Three-phase short-circuit fault occurring at point f2