腳手架理論在中職數學教學中的應用

【摘要】本文基于腳手架理論的內涵分析，論述腳手架理論對促進中職生數學學科核心素養的作用，提出運用腳手架理論開展中職數學集合教學的策略：分層設定目標，搭建目標腳手架，強化培養學生的探究意識；創設真實的教學情境，搭建學習情境腳手架，促使學生能力實現遞進式發展；關注學生的情感體驗，注重知識的反思回溯，搭建思想進階提升腳手架等。

【關鍵詞】腳手架理論 學科核心素養 中職數學教學 集合

【中圖分類號】G63 【文獻標識碼】A

【文章編號】0450-9889（2023）20-0084-04

《中等職業學校數學課程標準（2020年版）》（以下簡稱數學課標）指出，中職數學教師在教學時要準確把握教學要求、做好教學設計，合理運用各類教學資源，推動教學方式方法改革；要根據課標中的學業質量要求，重點考核學生運用知識發現與解決實際問題的能力，促進學生學科核心素養的發展。數學課標對促進學生數學學科核心素養發展做了明確闡述，這給中職數學教師推動學科教學改革指明了基本方向。在此背景下，中職數學教師應該從優化教學資源配置、創新教學理念、改進教學方法等方面著手，探索促進數學教學改革、發展學生學科核心素養的有效路徑。為此，筆者嘗試通過搭建教學“腳手架”的方式，推進“支架式教學”方法在中職數學教學中的應用，取得了較好的實踐探究效果。

一、腳手架理論的內涵

腳手架原是指工程建設中為推進施工進度、確保高層建設而搭建的施工平臺，由于其具有組合與遞進的特點，因此這一概念得以被引用到教育教學領域。教育領域腳手架理論的提出，最早可追溯到1976年，美國教育學家布魯納從建筑行業中得到啟發，首次提出了“腳手架”的概念，并進一步將其解釋為“支架式教學”。腳手架理論是以蘇聯心理學家維果斯基的“最鄰近發展區”理論為基礎和模板。維果斯基認為，兒童要解決的問題和兒童原有能力間可能存在差異，但兒童能夠在教師幫助下通過學習消除這種差異。這個差異就是“最鄰近發展區”。根據維果斯基的理論，布魯納認為在幫助兒童走向“最近發展區”的過程中，教師作為更富有經驗、具有更強認知能力的長者，通過搭建腳手架（或稱為“支架”）的方式，為學生鋪設進步的階梯，可以有效提高學生的學習效率，這也符合學生的認知心理特性。

具體而言，腳手架理論認為，當學生開始學習新的概念時，由于學生的知識儲備、經驗能力等尚欠缺，因此需要教師的主動支持，在教師的幫助、指導下展開有效的學習。在教師支持和幫助的過程中，學生通過主動思考、解決問題，從而獲得新知識、新技能，不斷發展和提高自身的學習能力。在學生開展學習的整個過程中，教師就像建筑行業中的腳手架，起到支持和指導學生學習、幫助學生發展進階的作用。

基于這樣的理解和認知，筆者近年將腳手架理論引入中職數學教學，進行了長時間的教學實踐研究。通過實踐研究，筆者認為腳手架理論在中職數學教學中的應用，有助于教師開闊專業視野、豐富專業知識儲備、轉變教育教學理念、改進教育教學方法，也有利于學生養成探究意識和提升知識遷移應用能力。尤其是就目前的實際情況而言，部分中職學校的數學學科教學仍然存在重分數輕技能、重理論輕應用的問題，這可能會阻礙學生數學思維的發育和發展，同時也不利于在其他專業教學中滲透數學知識，從而在一定程度上降低學生的專業學習效果。在這種情況下，在中職數學教學中引入腳手架理論，就具有重要的現實意義。

二、腳手架理論對促進中職生數學學科核心素養的作用

數學課標提出，中職數學學科核心素養主要包括數學運算、直觀想象、邏輯推理、數學抽象、數據分析和數學建模等六個方面。長期以來，在如何培養學生學科核心素養方面，有不少中職數學教師感到困惑，困惑點主要是如何有效開展學科核心素養培養工作。在實踐探究過程中，筆者發現腳手架理論能夠有效解決這一問題。

（一）有利于從建構主義視角促進學生數學學科核心素養的發展

在教學過程中，教師可以借助腳手架理論，從建構主義視角對數學知識進行科學分層，讓學生在完成各層次學習任務的過程中，促進自主學習能力的提升和學科核心素養的發展。在具體教學中，教師首先要科學設定分層目標，然后根據目標合理篩選、整合、安排分層教學內容，設計分層教學任務，幫助學生搭建起通向深度學習的腳手架，接著根據學生的學情和需求布置學習任務，以學習任務驅動學生積極參與學習、探究問題，從而有效落實核心素養的培養。要注意的是，在為學生搭腳手架、實施分層教學的過程中，教師要始終堅持以學生為中心的原則，任務為學生而設、活動為學生而開、支架為學生而建，切不可脫離學生學情隨意開展教學。

如在中職數學基礎模塊“集合的表示法”這一內容的教學中，教師可以通過創設有趣味的問題情境，激發學生的學習興趣，為學生深入學習這一知識搭建起腳手架，有效引導學生學習、探究和分析集合的表示方法，并在逐層解決問題的過程中掌握概念、厘清范圍，最后形成全面認知。為此，筆者在具體教學中設計了以下六個具有層次性的學習問題：①小于7的自然數有哪些？②中國古代的四大名著是哪幾部？③奧運會的田徑比賽包含哪些小項目？④方程式x2=x有哪些實數根？⑤方程x2-3x+2=0有哪些實數解？⑥以上問題涉及的數據，與我們今天學習的“集合”有什么關系？這幾個問題既有數學方面的問題，也有文學、體育方面的問題，而且與學生的學習、生活比較貼近，能夠有效激發學生的學習欲望。此外，在解決這些問題的過程中，學生逐漸對“集合”形成了客觀、具象的認識，初步掌握了集合的表示方法，發展了邏輯推理、數學抽象、數據分析等數學學科核心素養。在整個教學過程中，層次性學習問題就是助推學生學習的腳手架，教師就是搭腳手架的人，通過借助腳手架，筆者順利落實了學生數學學科核心素養的培養。

（二）有利于為學生數學學科核心素養進階鋪設路徑

只有教師正確認識腳手架在推進學生核心素養進階、拔升過程中的功能和意義，積極探索將腳手架理論常態化運用于數學學科日常教學的有效路徑，才能深入發展學生的學科核心素養。如，在日常教學中，教師可以根據學生實際設計探究性學習項目和實踐任務，并以這些項目和任務為腳手架引導學生通過合作探究、詢問教師等方式開展學習，使腳手架理論充分融入學生的日常學習，從而持續促進學生學習能力、學科核心素養的發展。教師還要注重學生與企業的互動實踐、學生與社會的聯系，將企業實習、社會實踐作為深入開展教學活動的抓手，作為搭建學生學習腳手架的“基底”，讓學生在真實的情境中學習、體驗、感悟，最終促進數學運算、直觀想象、邏輯推理等數學學科核心素養的發展。

由此可見，將腳手架理論融入中職數學教學，并與學生學科核心素養培育相結合，能夠產生積極的教學效果。因此，教師在教學中要始終堅持由易到難、由淺及深的教學思路，借助學習腳手架引導學生不斷深入學習基礎知識和技能、開展企業和社會實踐，促使學生將課堂所學知識遷移運用于解決生活中的實際問題，才能有效實現全面發展中職生數學學科核心素養的目標。

三、腳手架理論在中職數學集合教學中的應用策略

（一）分層設定目標，搭建目標腳手架，強化學生探究意識的培養

過去，由于部分教師存在“數學學科只要讓學生會算、懂算”的觀念，所以中職數學教學普遍存在以理論知識講授為主的現象。這種教學觀念和教學方法帶來的消極后果，是學生雖然能夠掌握一些基礎的運算技巧，但一旦碰到比較復雜的運算問題，就會感到無從著手。其中一個突出的表現是，分層教學目標難以科學設定，層次性學習難以有效推進，學生的探究意識難以得到發展。鑒于此，數學教師可以借鑒腳手架理論，通過科學設定分層目標為學生搭建學習腳手架，促使學生深入探究知識，并學會運用相關知識解決問題，從而不斷發展學生的邏輯推理、數學抽象、數據分析和數學建模等數學學科核心素養。

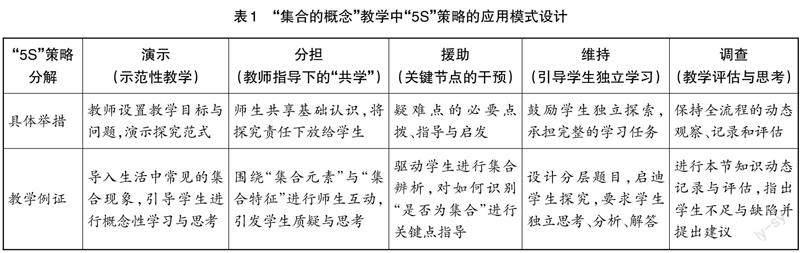
在具體教學中，教師首先要對學生學情進行調研，科學分析學生的學習能力、學習水平；然后要對相關知識點進行細化分解，再由淺入深、由粗及細地設計教學維度和分層教學目標；接著要根據不同的維度和目標設計探究性學習任務，為學生搭建起學習腳手架，從而不斷促進學生探究意識和探究能力的提高。以“集合的概念”這一內容的教學為例，教師可在教學中運用“5S”策略有效分解教學目標，為學生搭建學習腳手架，幫助學生在真實的教學情境中由淺入深地學習知識和技能，在“踏階而上”的過程中提升自身的綜合能力，從而取得遞進式的教學效果（如表1所示）。

由表1可知，“5S”策略包含演示、分擔、援助、維持、調查五部分，這是一個逐層遞進的教學過程，也是一種有助于促進學生學習的腳手架，目的在于引導學生拾級而上，形成探究性學習的意識和能力，不斷提高學習效果。以“集合的概念”這一內容的教學為例，筆者搭建學習腳手架的具體做法如下。筆者首先出示探究問題，對問題做適當講解，然后根據問題與學生共同開展探究性學習，在學生開展探究學習過程中進行適當點撥，并針對存在問題提出解決建議。在此基礎上，筆者讓學生獨立探究“集合的特征”（即如何辨析集合概念與現象）這一問題，引導學生嘗試總結集合的概念和集合的辨析方法，從而鞏固和提高學生的自學能力。最后，筆者先讓學生通過自評、互評的方式，嘗試總結在整個學習中自己遇到的難題和問題，再對學生的學習進行總結性評價，并給學生提出解決問題的建議和意見。

在教學中，筆者借助應用題展現集合的特征，重點講解集合的確定性、無差異性與無序性等特性，讓學生深刻理解集合的含義和基本特征。如在講解集合的“確定性”時，筆者首先舉出“個子高的女生”“比較小的杯子”兩個反面例子，引導學生嘗試表述這兩個例子的集合。當學生發現無法進行表述時，學生認識到只有確定性因素才能構成一個集合。又如在講解集合的“無差異性”時，筆者設計了這樣一道例題：有兩個集合A={1，2，3，4}，B={3，4，5，6，7}，把這兩個集合合并起來后得到怎樣的新的集合？新的集合與原來兩個集合有什么相同之處和不同之處？根據筆者的引導，學生很快合并出了新的集合{1，2，3，4，5，6，7}，并比較分析出三個集合的相同點和不同點，從而理解了集合的無差異性。

在教學過程中，筆者采取“5S”教學策略，首先展示案例進行演示教學，作為引導學生進入學習的腳手架，讓學生初步了解集合的概念和特性；然后通過設計探究性問題，作為學生開展進階學習的腳手架，引導學生自主學習、合作探究，讓學生在解決問題的過程中，深入理解集合的定義，以及辨析集合的方法；最后通過調查與評估，了解學生掌握概念和知識的程度，并針對學生存在的疑惑和問題，提出解決建議和辦法，這是幫助學生實現螺旋上升的腳手架。值得一提的是，并非“5S”策略的每一個步驟都要體現在教學中，教師要根據教學實際所需選擇合適的策略，避免出現“為策略而策略”的情況。

（二）創設真實的教學情境，搭建學習情境腳手架，促使學生實現遞進式發展

建構主義理論認為，在教學中突出學生的主體地位，驅動學生以自我為中心進行主動學習、積極探索，這樣的教學方式相較于由教師講授、由教師安排的教學方式，能取得更好的教學效果。而搭建學習腳手架的本質目的，就是通過創設生活化教學情境的方式，為學生營造熟悉、活潑且充滿溫度的學習氛圍，調動、激發學生的主觀能動性，讓學生在輕松愉悅的氛圍中發散思維、探究新知，從而不斷提高課堂教學有效性，促進學生學科核心素養的發展。

如在“集合的表示法”這一內容教學中，筆者通過設計生活化問題創設學習情境，為學生搭建學習集合知識的腳手架。筆者設計了這樣幾個生活化的集合問題：中國所有直轄市的集合、地球幾個大洋的集合、教室內所有椅子的集合、所有三角形的集合、1—100自然數的平方的集合。上述幾個問題涉及中職生比較熟悉的直轄市、椅子等生活事物，能夠有效拉近學生與問題的距離，激發學生思考與探究的興趣。

通過上述問題的導入，教師可以讓學生從直觀的生活現象入手，思考集合應該如何描述，進而在思考、分析中明確集合的表示方法。通過分析，前兩個集合可以采用“列舉法”進行表示：我國有北京、上海、天津與重慶四個直轄市，世界上有太平洋、大西洋、印度洋和北冰洋四個大洋。而關于第三個集合，學生可以通過數教室里的椅子得出。這幾個問題都與學生的學習或生活相關，既能夠有效激發學生的探究興趣，又能讓學生有效掌握表示集合的方法。在筆者的引導下，學生通過探討、思考，嘗試總結出集合列舉法的適用條件：①有限集合且元素不太多；②有較多元素的集合但存在一定規律，可以用省略法表示；③有規律的無限集合。為了進一步鞏固學生所學知識，筆者讓學生嘗試運用這一方法表示“所有三角形的集合”“1—100自然數的平方的集合”這兩個集合。

在教學過程中，筆者通過設計一連串問題創設生活化教學情境，以問題為抓手、以遞進思考為依歸，引導學生對集合的表示方法進行研究，使學生獲得對概念和解答方式的認知，為學生搭建起進階學習的腳手架，提高學生的知識遷移應用能力。

（三）關注學生的情感體驗，注重知識的反思回溯，搭建思維進階提升腳手架

學生是學習的主體，因此在搭建學習腳手架的過程中，教師一方面要關注學生的學習情感體驗，改變單純輸出知識的教學方式，豐富教學的多樣性意蘊；另一方面要注重驅動學生積極“回頭看”，養成對知識點的溫習、回溯和反思意識。無論是數學游戲、娛樂活動還是課堂互動探究，都是賦予學生更大自由度的教學方式，目的在于釋放學生的天性和熱情，促使學生獨立學習與深度探究。在此過程中，教師要發揮“指揮者”作用，搭建腳手架，提供輔助與指導，確保學生的知識反思與回溯達到預期目標。

在課堂教學中，教師通過游戲化教學方法優化學生的情感體驗，用生活化的活動使學生對數學知識形成多維度認知，有利于提高學生的學習效率。如在講解補集的知識時，筆者便將“狼人殺”游戲與補集的運算方法相結合，讓學生在玩游戲的過程中理解什么是補集，并掌握補集的運算方法。這種通過游戲增強學生的學習情感體驗的教學方法，能夠有效搭建起學習的腳手架，引導學生圍繞知識要點、疑難點進行反思與回溯，最終能夠有效促進學生能力的提高與核心素養的發展。

又如，在“集合的運算”教學結束后，教師引導學生溫習、反思，重點抓住疑難點和易錯點進行“回頭看”，驅動學生自主對相關知識點進行二次探索，鞏固知識結構、豐富知識體驗。為了更好地引導學生開展課后學習，筆者設計了“我們班愛好籃球與音樂的男生”“班內數學和語文成績都比較好的學生”“上個學期獲得過獎狀的男生和女生”等學習任務，讓學生運用交集、并集、補集的知識完成這些知識點的學習，學生在相互問詢、交流、探討的過程中，既鞏固了課堂所學，又發現了知識與日常生活的聯系，能夠有效激發學生的學習興趣。通過引導性學習任務的設置，讓學生形成知識回溯的意識和能力，進而在運用集合運算知識和技能的過程中優化反思體驗，增強知識應用黏性。

綜上所述，基于學生中心論和建構主義理論的腳手架教學方法，能夠有效激發學生的學習興趣，幫助學生在學習腳手架的支持下開展深度學習，從而促進學生學科核心素養的全面發展。而要想充分發揮腳手架理論的育人功能，教師應扮演好“指揮家”“驅動者”的角色，只有科學合理設定教學目標，細化教學策略與步驟，尊重學生的個體差異與身心特點，促使學生獨立學習、深入探究、關照現實、體察生活，才能不斷促進學生的全面發展。

參考文獻

［1］韓加增.中職數學分層教學模式下生活化策略的探索研究［J］.現代職業教育，2021（2）.

［2］賴小平.要為學生的猜測搭好思維的“腳手架”［J］.實驗教學與儀器，2018（7）.

［3］常鑫海.中職數學教學中存在的問題及解決策略［J］.甘肅教育，2020（2）.

［4］張曉方.中職數學教學中學生思維能力的培養［J］.當代教育實踐與教學研究，2020（11）.

［5］馮慧明.中職數學課堂融入核心素養的教學探究［J］.課程教育研究，2020（10）.

作者簡介：龍波（1981— ），廣西柳州人，講師，主要研究方向為中職數學教學。

（責編 蒙秀溪）