基于盲孔法的鋼絞線有效預應力檢測識別技術

張志國，吳冀橋，張彩亮，許 琪，陳葉鑫，王澤遠

(1.石家莊鐵道大學 土木工程學院，河北 石家莊 050043；2.石家莊鐵道大學 道路與鐵道工程安全保障省部共建教育部重點實驗室，河北 石家莊 050043；3.武漢江騰鐵路工程有限責任公司，湖北 武漢 430063；4.中國鐵道科學研究院，北京 100081)

近年來,預應力結構廣泛應用于橋梁、巖土等工程領域,有效預應力大小是衡量在役預應力結構工作性能的重要指標。鋼絞線作為鐵路預應力混凝土梁橋中預應力的主要載體,準確識別其有效預應力是在役鐵路橋梁安全性評判的重要內容,可降低結構因預應力失效而造成的梁體開裂甚至坍塌事故風險[1]。另外,國內諸如大秦鐵路、朔黃鐵路等面臨重載改造,鐵路橋梁中預應力鋼絞線有效預應力大小的識別對改造工程也有重要參考作用[2]。劉永前等[3]對朔黃鐵路等重載鐵路常用預應力混凝土簡支T梁梁端斜裂縫的產生機理進行了數值模擬及試驗研究,發現梁端最大主拉應力及剪應力隨梁體預應力損失的增大而增加,尤其在梁端截面中性軸附近位置處的最大剪應力增幅極為明顯,是梁端斜裂縫產生的重要因素。薛繼連[4]通過對朔黃鐵路39座橋涵結構進行原位試驗,以及對更換下來的32 m普通高度預應力混凝土簡支梁進行靜載開裂試驗,分析不同跨度及截面高度橋梁在大軸重載下的結構響應,并提出采用預應力碳纖維板加固梁體來提高其抗裂性能。目前,國內外識別鋼絞線有效應力的方法眾多,按照檢測方法特性可分為直接檢測和間接檢測,直接檢測法是利用檢測儀器直接拾取鋼絞線的位移、電磁、聲、波等物理信號,通過這些物理信號和鋼絞線有效預應力建立起對應關系,由此直接得到鋼絞線有效預應力的大小,常見的直接檢測方法有拉脫法、橫張增量法、振動法、波動法、電磁檢測法、超聲導波法、切割法等,這類方法存在較苛刻的使用條件,精度受測試過程影響較大、理論基礎尚不完善,有的方法還會對結構造成較大二次損傷等問題,導致難以在既有預應力混凝土梁橋結構有效預應力檢測中得以廣泛推廣。間接檢測方法常見于預應力混凝土梁的有效預應力識別,建立有效預應力和梁體結構力學特性之間的關系,通過一定手段檢測混凝土梁的性能再反算出鋼絞線有效預應力大小,常見的間接檢測方法有:局部應力釋放法、消壓彎矩法、動力測試法、等效質量法等[5]。由于混凝土材料本身的復雜性能特征,以及其性能還會隨時間產生徐變和劣化,加之預應力多束配置的相互影響,通過性能檢測再間接反推預應力的方法本身存在著先天不足,不可避免地會造成較大離散性和系統誤差,實際測試精度如何保證尚需進一步展開研究。另外,間接法還需要施加較大的載荷試驗,這在實際工程中,尤其對已存病害的橋梁實施具有較大的安全風險隱患,甚至是無法實現的。

綜上所述,盡管針對鋼絞線有效預應力已經探索了很多不同的檢測方法,但尚未形成一種公認的有效方法。鑒于當前國內外還沒有一種簡單有效、普適性強、精準可靠的鋼絞線有效預應力檢測方法,本文在已有研究基礎上,提出采用盲孔法識別鋼絞線有效預應力的方法,以期在檢測精度和對梁體局部破損之間尋找平衡點,建立一種新型的局部損傷檢測方法。這種局部損傷不至于對橋梁性能造成影響,而且可根據現行規范進行修補恢復。

盲孔法屬于局部應力釋放法中的一種,目前國內外對應力釋放法已有系列研究。1934年,Mathar[6]首次提出通過測量構件鉆孔后孔邊應變來確定金屬構件的殘余應力,后由Soete等[7]發展完善而形成較系統的理論方法。經過多年發展,逐漸形成了盲孔法、鉆孔法、環孔法、剝層法、開槽法等多種對金屬構件進行應力釋放及殘余應力識別的方法。Mainjot等[8]提出采用積分法來檢測不均勻殘余應力場的殘余應力,擴大了盲孔法檢測金屬殘余應力的適用范圍。

盲孔法從早期的檢測金屬構件殘余應力發展到現在的預應力混凝土構件檢測。1999年,楊勇等[9]提出了使用應力釋放法計算預應力混凝土梁預應力損失值的思路,并運用該法對某預應力T形剛構橋進行有效預應力檢測。2003年,戴福隆等[10]提出用云紋干涉法測量位移信息代替應變片測量應變信息來確定鉆孔法的孔周殘余應力,得到了鉆孔釋放的位移與殘余應力的關系。2009年,劉玲晶[11]對一片3 m長預應力混凝土梁進行了環孔法試驗研究,分析了鋼束位置對測點應力釋放值的影響,并給出了估算現存預應力的經驗公式。2010年,英國學者Schajer[12]分析總結了鉆孔法這些年取得的進展,并指出在有著先進溫度控制、振動隔絕的實驗室中利用光纖技術測量鉆孔表面微量位移將成為有效預應力檢測未來的發展方向。2012年,周晶[13]使用有限元軟件對預應力混凝土小箱梁進行建模,在箱梁跨中底板進行鉆孔,分析了改變孔深、孔徑時孔周邊的應力分布情況以及對應力集中系數的影響。2014年,劉志勇[14]以既有鐵路簡支T梁為研究對象,采用開槽法、消壓彎矩法以及結合理論計算對試驗梁的預應力損失進行了識別,證實了開槽法在實際工程中具有一定可行性。2015年,Bl?dorn等[15]提出盲孔法鉆孔時若沒有適當控制時,可能在孔壁中引入額外的應力,繼而影響盲孔法測量的準確性。2018年,毛碩[16]通過對一片預應力混凝土T梁進行ANSYS有限元建模模擬和現場試驗相互印證的方法得出,開槽法試驗應力釋放至零的切割深度與兩條平行槽間距之比為0.32～0.34,且數值模擬了相同尺寸的環孔、方孔、平行槽的應力釋放為零的開槽深度,發現開槽深度與開槽的方式基本無關。2019年,Lee等[17]提出一種基于應力釋放法(SRM)和數字圖像相關法(DIC)相結合的混凝土結構靜態應力估算方法。與應變計的逐點測量相比,DIC獲得的全場位移數據量更大,估算結果精度更高。2020年,馬騰[18]對聯合加載應力釋放過程進行了研究,發現通過施加一定大小的荷載消壓,可以減小開槽法應力釋放的深度,工程上可以利用這一點減小開槽法檢測有效預應力時對梁體的損傷。

本文在金屬構件及混凝土應力釋放法現有研究基礎上,提出在鋼絞線上鉆盲孔來識別鋼絞線有效預應力的方法,通過ANSYS有限元軟件對預應力混凝土常用七絲鋼絞線鉆孔過程進行仿真計算來探索鋼絞線鋼絲鉆孔后孔邊應力釋放規律,并對影響應力釋放過程的鉆孔參數進行影響規律分析,以獲取合適的鉆孔參數,來指導鋼絞線實際鉆孔試驗,并驗證鉆孔應力釋放規律的正確性及鉆孔參數的合理性;同時,據試驗結果建立鉆孔后孔邊應變釋放量與鋼絞線有效預應力之間的函數關系,并對其誤差及其適用性進行分析。

1 基本假定與盲孔法基本原理

基于盲孔法識別預應力鋼絞線,主要遵循以下基本假定:

(1)線彈性假定。鋼絞線在鉆孔過程中除鉆孔位置外,其周邊材料仍處于彈性受力狀態,各根鋼絲均處于彈性工作階段。

(2)均勻性假定。鋼絞線張拉后,遠離邊界條件的區域,外圍鋼絲的應力狀態基本相同。

(3)單向應力狀態假定。鋼絞線鋼絲受拉后近似處于沿軸向單向受拉應力狀態。應力釋放過程中假定各鋼絲之間接觸面摩擦系數保持不變。

本文盲孔法是借鑒在混凝土表面開槽、鉆孔等應力釋放識別法以及鋼板表面鉆孔反算殘余應力方法基礎上,考慮鋼絞線本身結構組成及受力特征,把張拉后鋼絞線各組成鋼絲近似看作處于軸向受拉的單向應力狀態,通過采用專用合金鉆頭在鋼絲直徑上鉆某一深度、一定直徑的盲孔后,測得孔邊釋放應變,由此反算出鋼絲有效應力,進而得到整根鋼絞線有效應力的一種方法。該法的核心是建立鉆孔釋放應變和鋼絞線有效預應力之間的關系,具體實施時,可以將仿真模擬和試驗驗證相結合,建立反映二者之間關系的擬合公式,然后隨工程應用數據積累不斷完善。

2 鋼絞線鉆孔精細化分析模型

本文采用ANSYS軟件進行仿真計算,模型采用8節點Solid185實體單元建立,將鋼絞線縱軸線方向設為z軸,將鉆孔方向設為y軸,x軸垂直于z-y軸所構成的平面,見圖1。鋼絞線兩端邊界條件為一端固定,一端張拉。七絲鋼絞線的建模參數取自規范GB/T 5224—2014《預應力混凝土用鋼絞線》[19]與GB/T 5223—2014《預應力混凝土用鋼絲》[20],采用1860級鋼絲和鋼絞線,具體數值見表1。

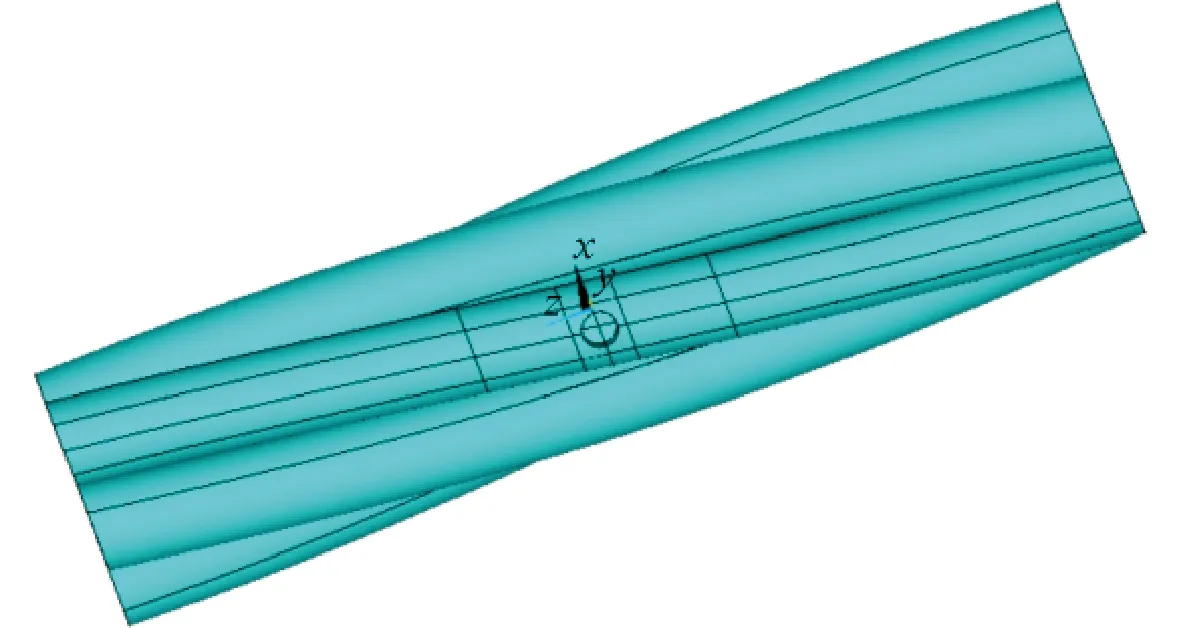
圖1 鋼絞線鉆孔有限元模型

表1 1×7鋼絞線幾何及力學參數

本研究主要探討鋼絞線在線彈性階段張拉鉆孔應力釋放規律,鋼絞線鋼絲采用彈性本構模型建模,由于模型是基于鋼絞線單根鋼絲的精細化建模,故模型彈性模量應以單根鋼絲的為準,本文取鋼絲彈性模量E=2.05×105MPa。模型長度經過多組仿真結果對比,綜合考慮計算精度和計算效率,選取60 mm長度建模。鋼絞線之間的接觸關系采用面面接觸,通過查閱相關文獻[21],接觸單元選擇Targe170和Conta174,建立外圍鋼絲之間、外圍鋼絲與中心鋼絲之間共計12對接觸對,接觸面之間的摩擦系數取0.15,考慮標準接觸行為,采用系統默認的增廣Lagrange乘子法進行接觸計算。單元網格劃分采用六面體網格,對于要進行鉆孔的鋼絲,鉆孔區域周圍網格尺寸采用0.1 mm,孔邊應力釋放區網格尺寸采用0.2 mm,遠離應力釋放區網格尺寸采用1 mm,對于不需進行鉆孔的中心直鋼絲和外圍其他5根螺旋鋼絲,網格尺寸均采用1 mm,網格劃分采用體掃略和體映射相結合方式,見圖2。

圖2 七絲鋼絞線鉆孔后網格劃分

模型的仿真計算過程為先張拉,后鉆孔。最大張拉力按工程施工常用張拉控制應力σcon=0.75fpk=1 395 MPa進行施加,鉆孔參數由鉆孔半徑和鉆孔深度確定,將鉆孔半徑分別取0.50、0.75、1.00、1.25、1.50 mm五種規格,鉆孔深度分別取1.0、1.5、2.0、2.5、3.0 mm五種情況,共形成25組不同孔徑、鉆孔深度的組合工況,為方便實際操作僅考慮在外絲外表面進行鉆孔,用符號RaHb表示各組合工況參數,含義為Ra代表鉆孔半徑和半徑大小,Hb代表鉆孔深度和深度數值。

3 仿真結果及參數影響分析

3.1 鋼絞線鉆孔應力釋放仿真計算結果

為便于描述仿真試驗結果,作如下定義:將鋼絲節點距離鉆孔左右邊緣的z向(鋼絞線軸向)距離定義為孔邊距;將鉆孔前后,鋼絲表面孔左右兩邊節點處的z向應力差值定義為這一節點的應力釋放量;某一節點應力釋放量與鉆孔前應力的比值被稱為該節點的應力釋放率。

以鋼絞線R0.5H1.5工況模型為例展示仿真結果,鉆孔前后,鋼絞線的z向應力云圖見圖3。

圖3 鉆孔前后鋼絞線z向應力云圖(單位:MPa)

圖3(a)、圖3(b)顯示了鋼絞線受拉后的應力云圖,由于存在邊界條件、鋼絞線各絲間復雜接觸關系的影響,從整體上看,圖3(a)中鋼絞線應力分布關系比較復雜,似乎缺少規律性。但在距離邊界較遠的模型跨中附近,應力云圖表現出明顯規律性,從跨中截面z向應力云圖可以看出,中心鋼絲的應力比外圍鋼絲應力大,且外圍鋼絲截面應力分布并非均勻,而是分層分布,靠近中心鋼絲的內層應力比遠離中心鋼絲的外層應力大,這一規律與鋼絞線各根鋼絲間復雜的扭絞接觸關系相符合。

圖3(c)、圖3(d)顯示了鋼鉸線鉆孔后的應力云圖。鋼絞線鉆孔后,被鉆孔鋼絲孔邊附近出現應力重分布現象。沿鋼絞線軸線方向,孔邊拉應力釋放為零甚至變為壓應力,隨孔邊距的增加,應力釋放量逐漸減小。沿鉆孔上下邊緣,孔邊產生應力集中效應,應力集中系數最大值為2.982,應力集中效應在遠離鉆孔上下邊緣時逐漸削弱。沿鉆孔深度方向,在孔深范圍內鋼絲內部應力分布與表面分布規律相同,未鉆通部分由于截面削弱應力增加。

通過ANSYS路徑命令,提取出鉆孔前后孔左右邊緣鋼絲表面沿軸線方向5 mm范圍內節點的z向應力值,二者相減得到此工況下孔邊節點應力釋放量,進而求得孔邊節點應力釋放率,將數據繪制成曲線,見圖4。

圖4 工況R0.5H1.5時鋼絞線孔邊應力釋放規律

從圖4可以看出,應力釋放量曲線與應力釋放率曲線隨孔邊距的變化趨勢相同。隨著孔邊距增加,應力釋放量(率)逐漸下降,且下降趨勢由陡峭趨于平緩。從數值上看,在孔邊距為0 mm節點處,鉆孔后的應力釋放量為1 321.9 MPa,應力釋放率為98.52%;在孔邊距5 mm節點處,鉆孔后的應力釋放量為30.4 MPa,應力釋放率為2.25%。孔邊距超過5 mm后,孔邊節點應力幾乎不受鉆孔影響,由此表明鉆孔應力釋放過程發生在孔邊小范圍內,遠離孔邊的鋼絲節點應力幾乎不受鉆孔影響。

3.2 影響鉆孔應力釋放的參數分析

對鉆孔半徑分別為0.50、0.75、1.00、1.25、1.50 mm,鉆孔深度分別為1.0、1.5、2.0、2.5、3.0 mm,共25種不同工況模型進行鉆孔仿真計算,提取出各種工況下鉆孔左右邊緣5 mm范圍內的應力釋放量繪制成曲線。

圖5為在不同鉆孔半徑下,鉆孔深度對鋼絞線孔邊應力釋放值的影響。

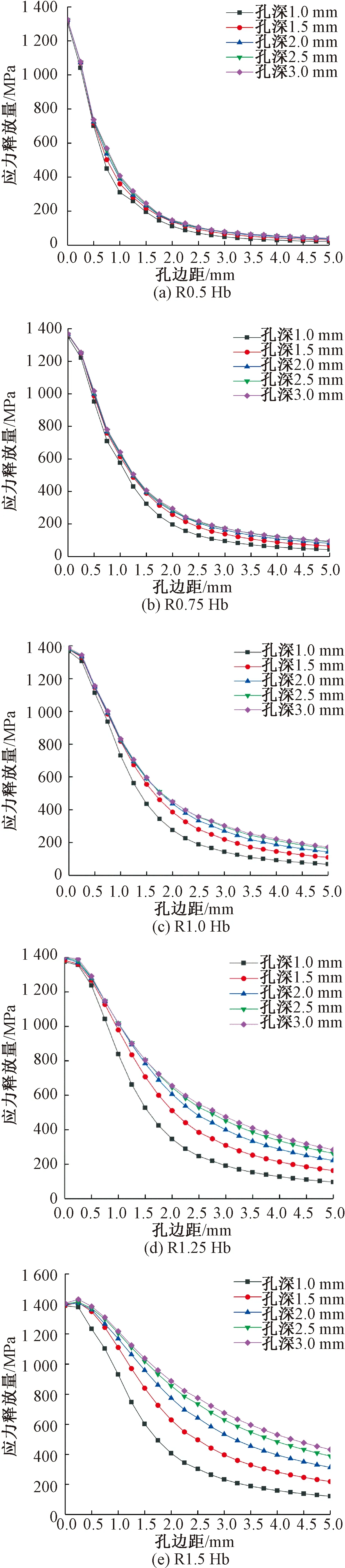
圖5 鉆孔深度對孔邊應力釋放量的影響

從圖5可以看出,在同一尺寸鉆孔半徑工況下,孔邊同一位置處鋼絲應力釋放量均隨鉆孔深度的增加而增加,最終趨近收斂,曲線收斂速度隨鉆孔半徑的增大而減緩。引入深徑比(孔深與孔徑之比)來表達應力釋放曲線的收斂情況,對上述5種不同孔徑工況,若相鄰兩條應力釋放曲線上各點的應力釋放率差值的平均值k<1.5%,則認為在該鉆孔深度下應力釋放曲線已經收斂,該工況在此鉆孔深徑比下已完成孔邊應力釋放,k的表達式為

( 1 )

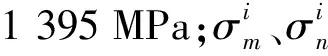
經計算可得,當鉆孔半徑為0.5 mm時,工況R0.5H1.5與R0.5H2.0之間的k=1.3%,孔邊應力完成釋放的深徑比在3.0左右;當鉆孔半徑為0.75 mm時,工況R0.75H1.5與R0.75H2.0之間的k=0.9%,孔邊應力完成釋放的深徑比在2.0左右;當鉆孔半徑為1.0 mm時,工況R1.0H2.0與R1.0H2.5之間的k=0.7%,孔邊應力完成釋放的深徑比在2.0左右;當鉆孔半徑為1.25 mm時,工況R1.25H2.5與R1.25H3.0之間的k=0.4%,孔邊應力完成釋放的深徑比在2.0左右;當鉆孔半徑為1.5 mm時,在鉆孔深度小于等于3.0 mm時,工況R1.5Hb各條相鄰兩曲線之間的k最小值為1.8%,計算范圍內孔邊應力釋放曲線未達到收斂。

從上述計算結果可以看出,在進行盲孔法鉆孔試驗時,在孔徑取為0.50、0.75、1.00、1.25 mm時,理論上控制深徑比在2.0～3.0之間,即可實現鉆孔孔邊應力的穩定釋放。從中不難得出,當所選取鉆孔的孔徑越大,為完成孔邊應力釋放所必需的鉆孔孔深也要隨之增大,對鋼絲截面造成的削弱也就越嚴重,所以在實際進行鉆孔釋放時,選取鉆孔孔徑越小越有利。

圖6為在不同鉆孔深度下,鉆孔半徑對鋼絞線孔邊應力釋放值的影響。由圖6可以看出,在孔邊距一定的條件下,鋼絞線鋼絲應力釋放量隨鉆孔半徑的增大而增大,且鉆孔越深,鉆孔半徑對應力釋放量的影響越大。越靠近孔邊位置,鉆孔鋼絲應力釋放量越大,曲線變化越陡,在一定范圍內漸趨平緩。在孔深一定時,隨孔徑增加,應力釋放曲線沒有出現收斂態勢,但在孔邊距超過2 mm后曲線逐漸趨于平緩,所以通過選定鉆孔半徑再進行合理孔深確定更具合理性。

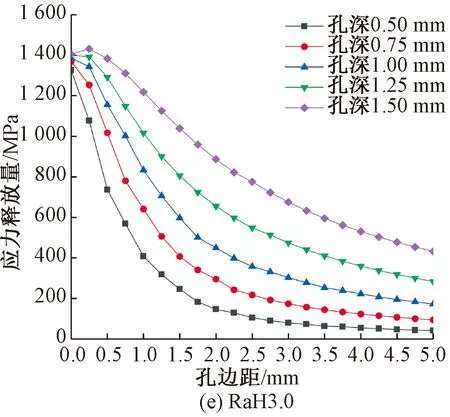
圖6 鉆孔半徑對孔邊應力釋放量的影響

根據上述仿真結果,可以得到預應力混凝土梁常用公稱直徑為15.2 mm七絲鋼絞線在利用盲孔法進行有效預應力識別時的鉆孔參數。為使鋼絞線孔邊應力完成穩定釋放,且盡量減小鋼絲截面受損面積的原則,同時鉆孔操作易于實現的要求,取基準鉆孔半徑0.5 mm,最大鉆孔深度可取2.0～3.0 mm,選取外側鋼絲進行鉆孔釋放試驗。

試驗時通過應變片測量測點鉆孔前后的應變變化,為使測量結果精度更高,應變片的粘貼位置應選擇應變釋放量值明顯,曲線收斂,且應變變化較為平緩的區域。對于試驗鉆孔參數的選擇,結合模擬分析結果將應變片粘貼在孔邊距為2 mm處比較合適。

4 盲孔法識別鋼絞線有效預應力試驗驗證

4.1 試驗概況

為驗證仿真計算得出的鋼絞線鉆孔后孔邊應力釋放規律的正確性,以及進一步探索鋼絞線有效預應力與孔邊應力釋放量之間的關系。試驗采取的鉆孔參數基于仿真計算結果,為進行數據比較,試驗時取基準鉆孔半徑為0.50 mm,對照鉆孔半徑為0.75 mm共兩種鉆孔規格,鉆孔深度取1.0、1.5、2.0、2.5、3.0 mm五種,測點為鉆孔鋼絲上距鉆孔邊緣2 mm處位置以及相鄰鋼絲與鉆孔位置同一截面處。本次試驗鋼絞線采用天津大強鋼鐵有限公司生產的1×7-φ15.2-1860級鋼絞線,其樣品實測參數見表2。

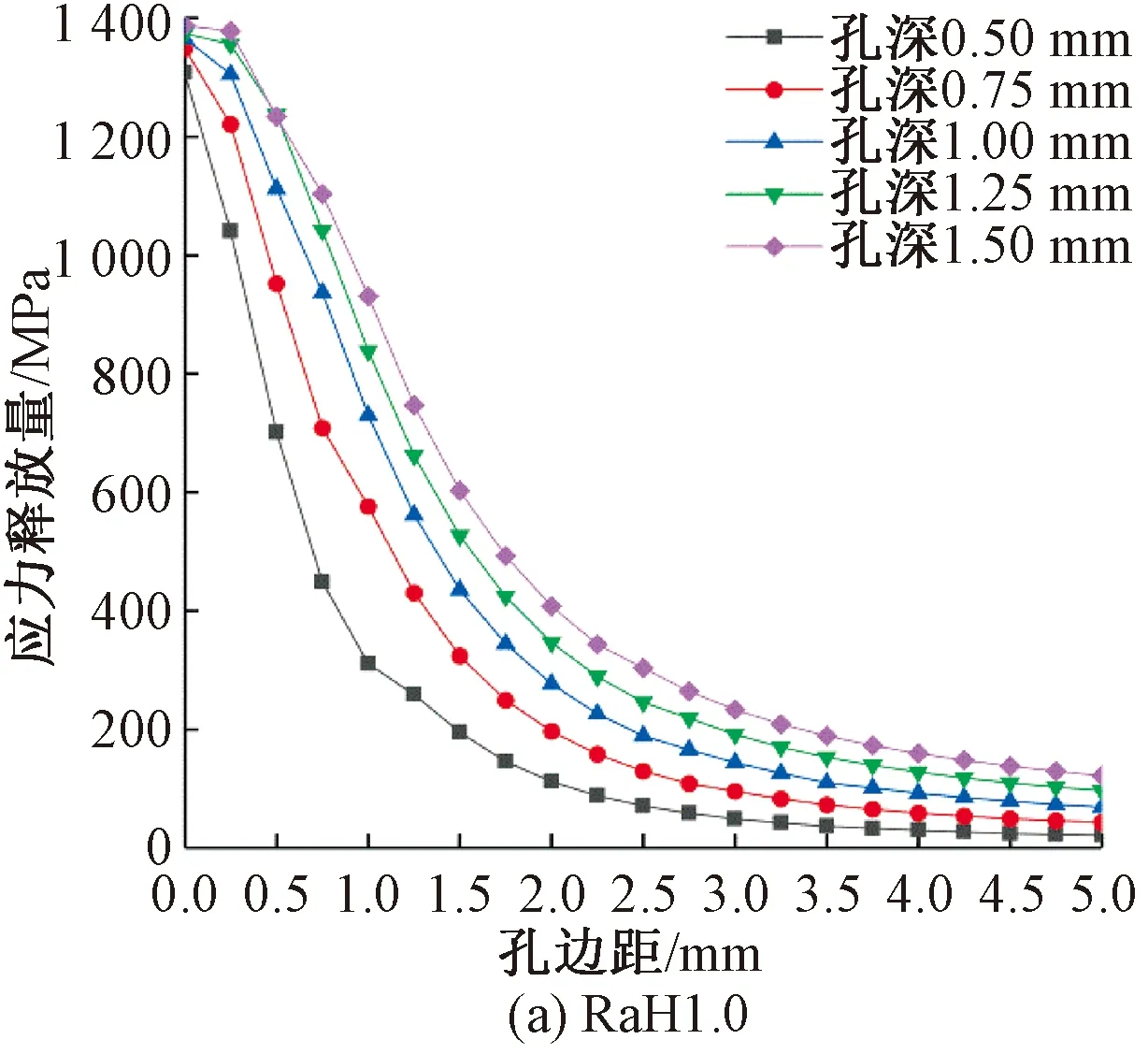
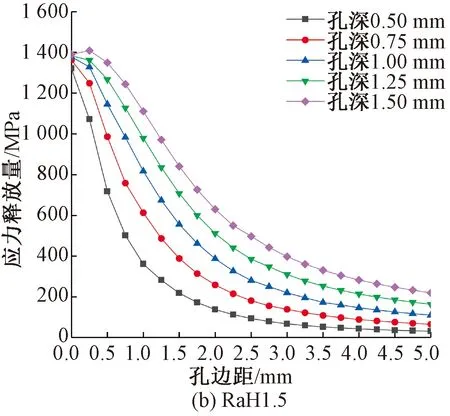
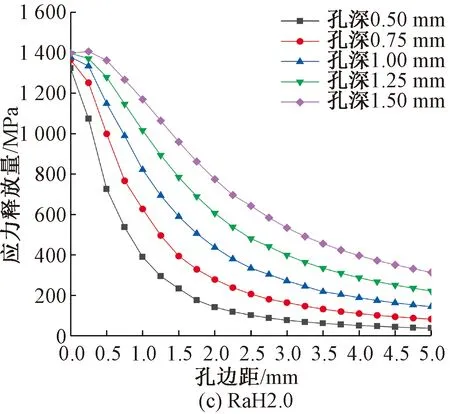
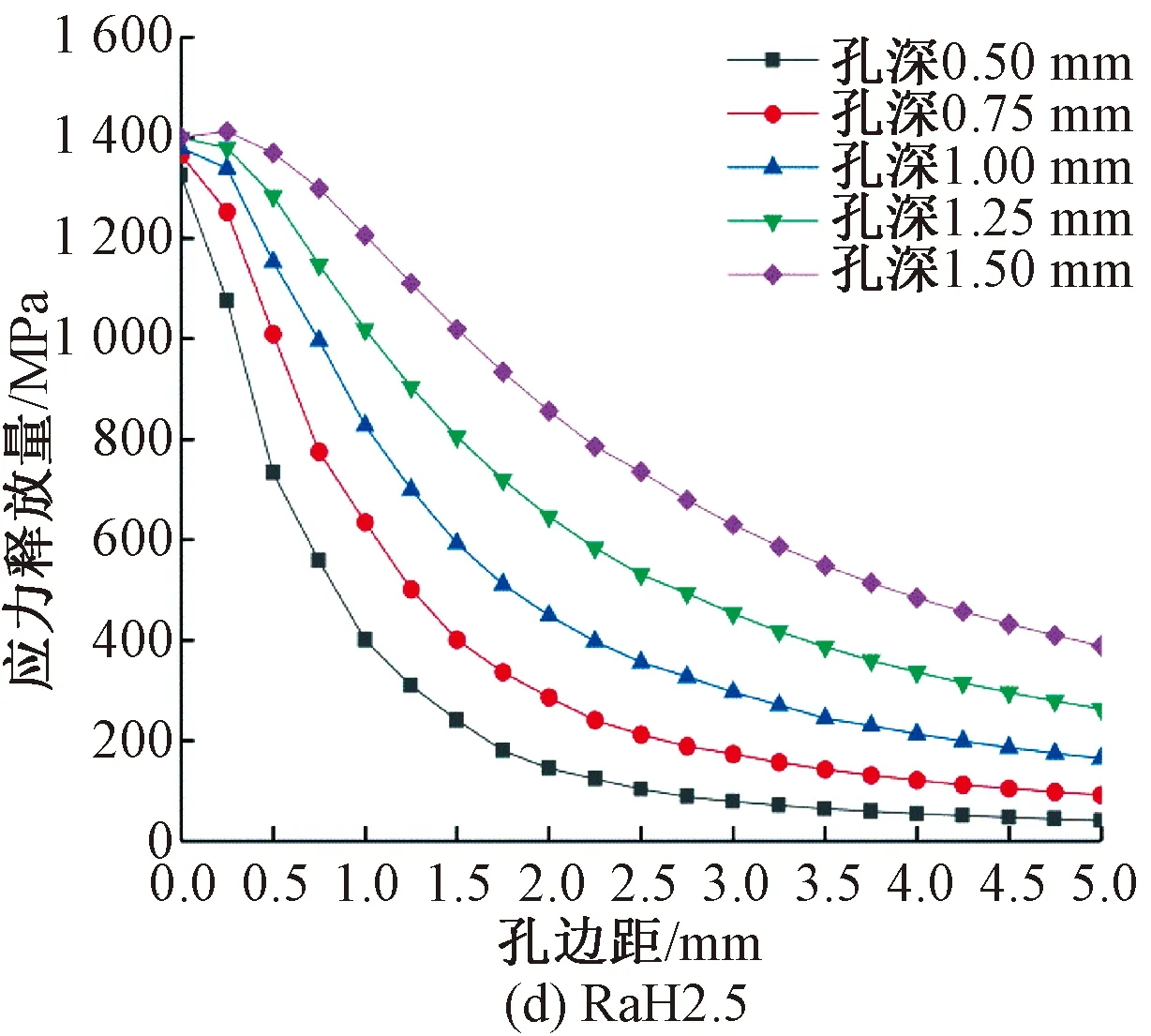
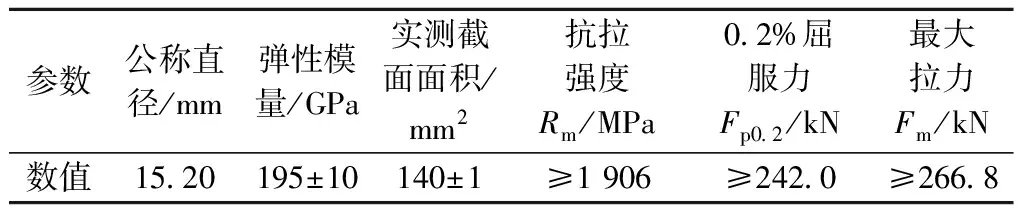
表2 試驗用鋼絞線參數

本試驗采用應變片測量鉆孔前后的應變變化,為方便描述,用應變釋放量代替仿真計算中應力釋放量進行討論分析。具體試驗流程為:

①試驗鋼絞線的截取。截取(105±5)cm長度鋼絞線若干用于張拉鉆孔試驗;②應變片粘貼。每根試件粘貼三枚應變片,具體見圖7;③鋼絞線張拉及鉆孔。利用夾具將試件固定在萬能試驗機上,通過萬能試驗機的電控系統設置張拉參數進行鋼絞線張拉持荷,待達到預定張拉應力后對鋼絞線鉆孔。

本試驗共設置10組不同工況下的鋼絞線進行鉆孔,每組工況試驗兩次,具體包括:外絲鉆孔半徑0.5 mm工況8組,編號1～8。每組鉆孔深度1.0～3.0 mm,初始張拉力分別為0、0.2σcon、0.4σcon、0.6σcon、0.7σcon、0.8σcon、0.9σcon、1.0σcon;外絲鉆孔半徑0.75 mm工況2組,編號9、10。每組鉆孔深度1.0～3.0 mm,初始張拉力分別為0、1.0σcon。其中,1和9組試驗為無應力下的鋼絞線鉆孔,其目的在于得到鋼絞線鉆孔時產生的加工應變;2～8組為鉆孔半徑0.5 mm時分別施加0.2σcon、0.4σcon、0.6σcon、0.7σcon、0.8σcon、0.9σcon、1.0σcon張拉應力時的鋼絞線鉆孔試驗,其目的在于建立鋼絞線鉆孔后孔邊應變釋放量和有效預應力之間的關系;10組為鉆孔半徑為0.75 mm時張拉力為1.0σcon的鋼絞線鉆孔試驗,通過和8組試驗數據對比驗證鋼絞線孔邊應變釋放量受鉆孔半徑的影響規律。

4.2 盲孔法試驗結果

4.2.1 無應力下鋼絞線鉆孔試驗結果

對1組和9組試件進行無應力下鉆孔試驗。得出鉆孔時鉆頭擠壓作用以及鋼絞線內部殘余應力釋放對待測點位應變的影響,對測量結果取平均值,得到不同鉆孔半徑、鉆孔深度下的鋼絞線無應力鉆孔加工應變,見表3。

表3 鉆孔加工應變量

從表3可以看出,隨鉆孔深度和鉆孔半徑的增加,鉆孔加工應變持續增大,為更精確測得鋼絲鉆孔后的應變釋放量,將下文鉆孔后所測數據均扣除相應鉆孔加工應變量后列出。

4.2.2 有應力下鋼絞線鉆孔試驗結果

將鋼絞線在萬能試驗機上張拉到預定荷載,然后對已標記的點位進行鉆孔,鉆孔前后通道1和2測得的應變釋放量的平均值作為該試件平均應變釋放量,將各組兩次試驗得到的平均應變釋放量取均值得到該組工況下的鋼絞線鉆孔孔邊應變釋放量平均值,各組工況下應變釋放量平均值隨鉆孔深度的變化曲線,見圖8。

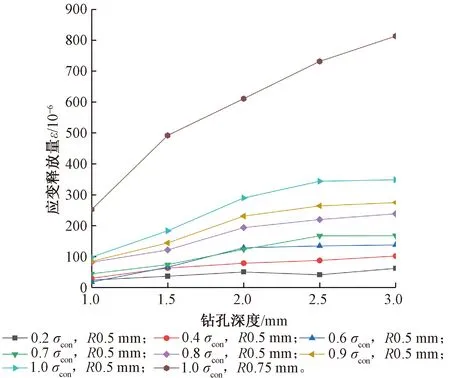
圖8 不同工況應變釋放量隨鉆孔深度的變化

由圖8可以看出,鉆孔半徑為0.5 mm的試件,隨張拉力和鉆孔深度的增加,孔邊應變釋放量均呈現增大趨勢,且當鉆孔深度超過2.0 mm時曲線開始收斂,隨張拉力逐漸增大,鉆孔加工應變等因素的干擾愈發微弱,曲線的變化趨勢更為一致。

鉆孔半徑為0.75 mm試件的孔邊應變釋放量要遠大于同等張拉力下鉆孔半徑為0.5 mm的試件,且在鉆孔深度由1.0 mm變化到3.0 mm的過程中,應變釋放量持續增大,沒有收斂態勢。曲線所顯示出的鋼絞線鉆孔孔邊應變釋放規律與仿真計算所得基本一致,但又有所區別。仿真計算得出,鉆孔深徑比在2.0～3.0時,應力釋放曲線已達收斂,然而經過試驗,發現鉆孔半徑0.5 mm孔邊應變收斂深徑比在4.0～5.0,收斂速度明顯慢于仿真計算值,經過分析,發現實際鉆孔的形狀為上粗下細的子彈頭狀,有別于仿真模擬的圓柱狀,從而使二者收斂速度產生差異,見圖9。

圖9 鉆孔形狀(單位:mm)

通過改變模型中鉆孔形狀,使其成為尾部為半徑0.5 mm半球的子彈頭狀,再次進行仿真計算分析驗證。與圓柱狀小孔相比,子彈頭狀小孔內部邊緣更趨光滑連續,仿真計算結果表明,在同等鉆孔深度下,后者孔型情況鋼絞線鋼絲同一位置處鉆孔后孔邊應力釋放率更低,應力釋放量收斂速度更為緩慢,收斂深徑比更大,且與鉆孔試驗結果更接近,表明上述修正后的孔型具有合理性,可信度也更高,二者收斂深徑比對比結果見表4。

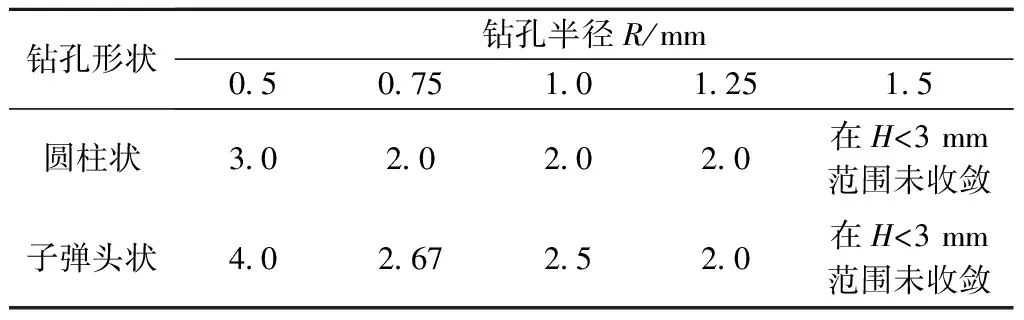
表4 兩種孔型鉆孔應力釋放量收斂深徑比對比

另外,通過分析每組試驗通道3的數據發現,在鉆孔過程中相鄰鋼絲與鉆孔鋼絲間的接觸摩擦力對鉆孔鋼絲鉆孔后的應力重分布過程起了限制作用,削弱了鋼絲鉆孔后的拉伸效應,進而導致相鄰鋼絲在二者相互作用下應變增加,且隨張拉力、鉆孔深度、鉆孔半徑的增加,相鄰鋼絲的應變增幅逐漸變大。以鉆孔半徑0.5 mm,鉆孔深度2.5 mm,初始張拉應力 1 395 MPa 張拉鉆孔工況為例,張拉至預定張拉力后3通道應變讀數(με)為2 311.0,鉆孔后3通道應變讀數(με)為2 504.0,鉆孔后相鄰鋼絲應變與鉆孔前應變之比為1.084。以上分析表明,鉆孔鋼絲應力釋放后,由于相鄰鋼絲間接觸擠壓及其摩擦作用,相鄰鋼絲應變出現增加,根據本文試驗結果最大增長比率在5%～8%范圍內。由于本文有效預應力識別擬合公式是以試驗結果為基礎,實際上已計入這個應力重分布的影響,而且其對應力釋放量影響較小,對鋼絞線有效應力識別效果不會造成影響。

4.2.3 鉆孔應變釋放量與鋼絞線有效預應力關系

前面分析得出鋼絞線鋼絲鉆孔后孔邊應變釋放量是隨孔深的增加逐漸增加直至收斂,通過鉆孔半徑0.5 mm試驗數據及曲線圖可以看出,當鉆孔深度超過2 mm時,應變釋放量曲線開始收斂;當鉆孔深度達到2.5 mm時,應變釋放量基本不再隨孔深變化。這一規律為尋找鋼絞線盲孔法試驗時鉆孔應變釋放量與有效預應力之間的定量關系提供了前提條件。下面基于試驗得到的鉆孔半徑0.5 mm,鉆孔深度2.5 mm工況下的實測數據對鉆孔應變釋放量與有效預應力之間進行最小二乘法曲線擬合。每組試驗做2次,每次試驗得到通道1和2兩組數據,在某一初始應力下按上述工況鉆孔獲取的數據共4組。擬合曲線見圖10。

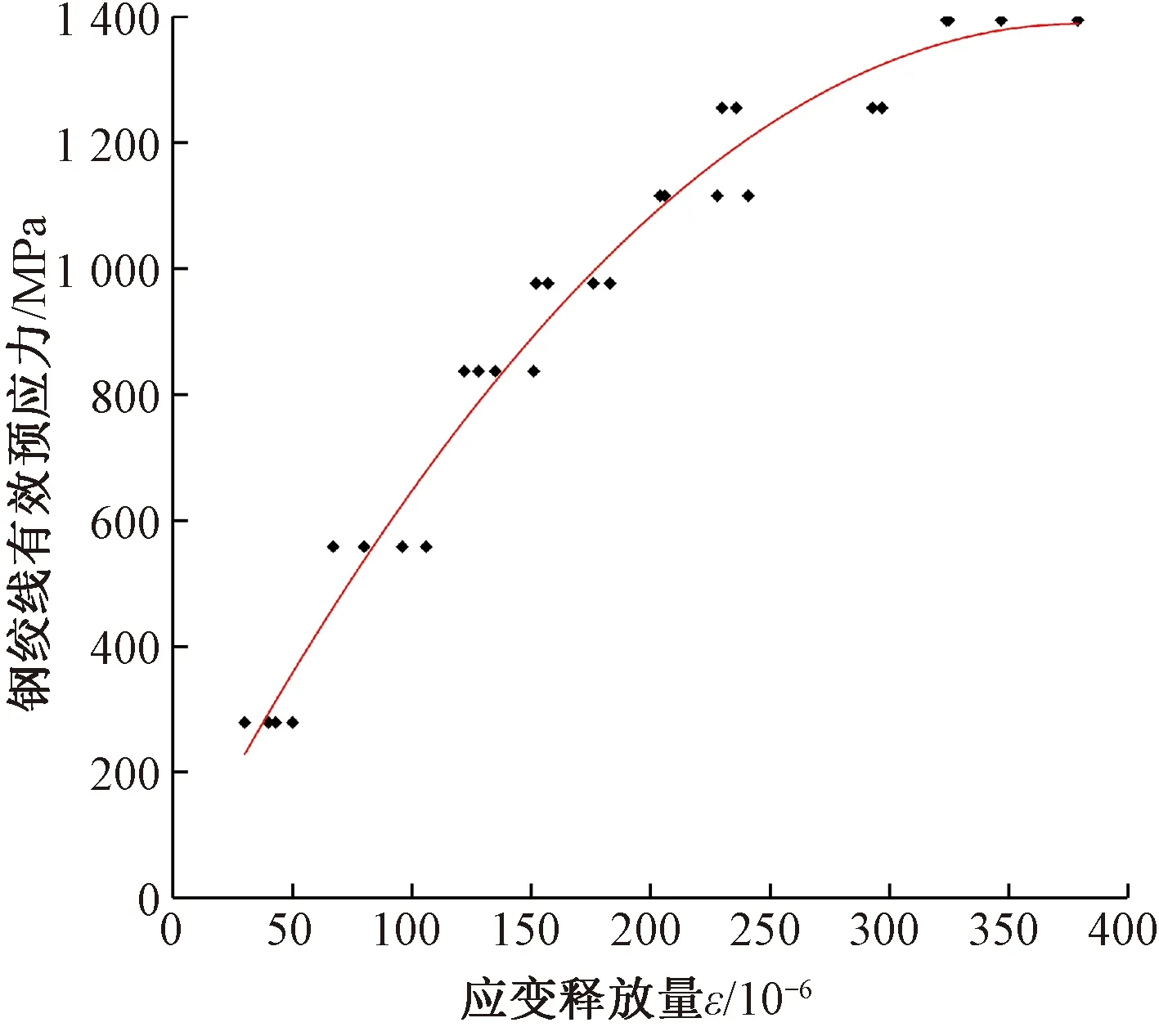
圖10 鉆孔應變釋放量與有效預應力擬合曲線

擬合函數為二次函數曲線,其方程為

( 2 )

式中:Tc為鋼絞線有效預應力計算值;εrs為測點處的應變釋放量實測值。擬合曲線的相關系數R2=0.974 1,表明擬合程度較好。

為減小偶然誤差,取同一試件上通道1和2的應變釋放量的平均值計算鋼絞線有效預應力值。為檢驗擬合公式計算出的有效預應力和實際有效預應力之間的誤差情況,現將實測數據代入式( 2 )得到對應有效預應力計算值,可求出有效預應力計算值Tc與真實值T之間的相對誤差K為

(3)

圖11所示有效預應力計算值Tc與真實值T之間近似呈線性關系變化。經誤差分析得到,有效預應力的擬合計算值和真實值之間的相對誤差最大值僅為8.82%,且超過85%的數據相對誤差在7%以內。以上數據證明利用擬合公式識別該類鋼絞線有效預應力具有一定的可信度,可以作為該類鋼絞線盲孔法識別有效預應力的經驗公式使用。

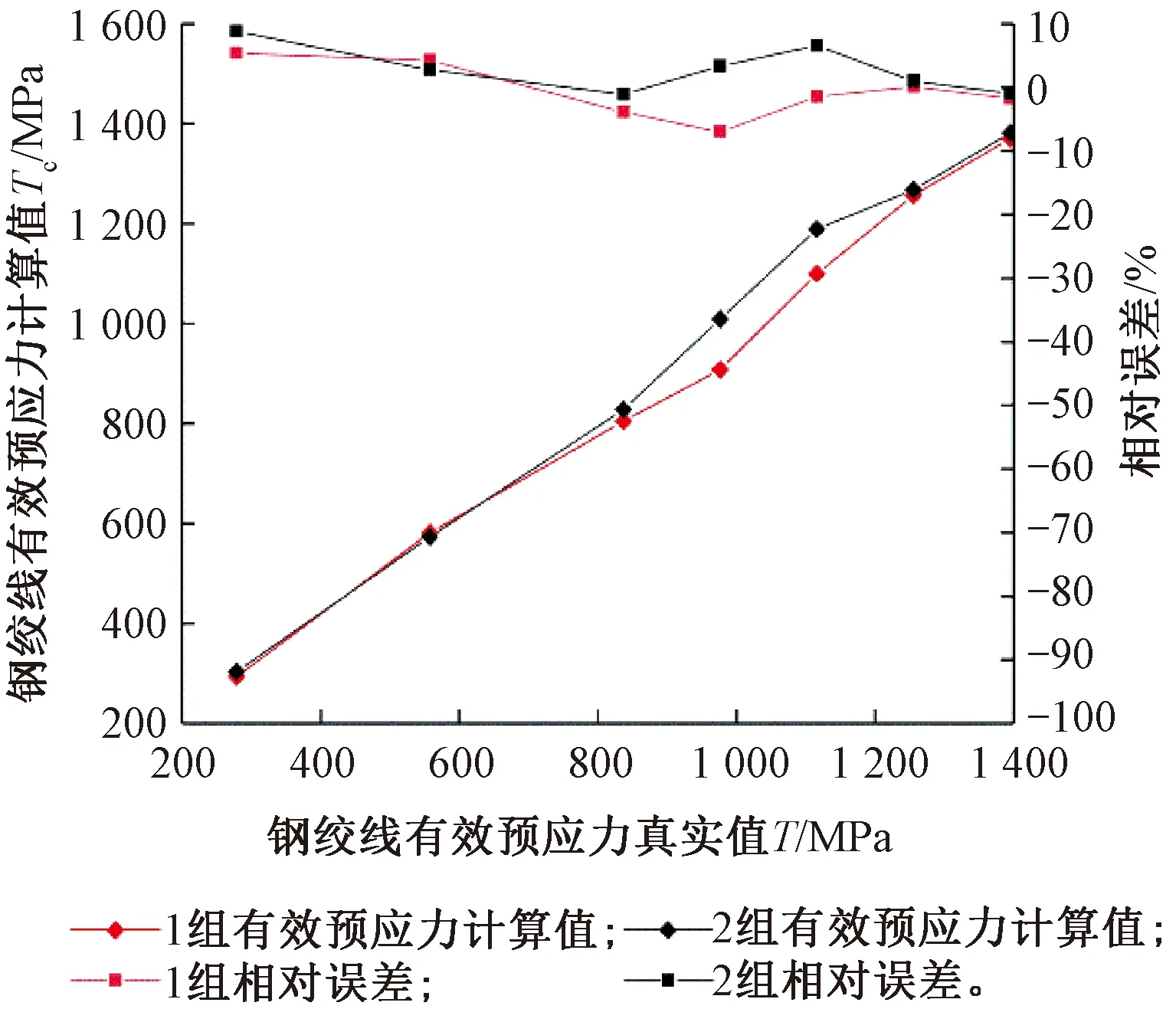
圖11 有效預應力真實值與計算值關系曲線

5 結論

本文針對既有預應力混凝土橋梁鋼絞線有效預應力識別這一技術難題,在現有研究基礎上,提出了鋼絞線鋼絲盲孔法進行有效預應力識別計算的基本方法,通過理論仿真分析,結合試驗結果驗證和分析,主要得出以下結論:

(1)鋼絞線鉆孔后孔邊應力釋放量及應力釋放率隨孔邊距的增大逐漸下降,且下降趨勢由陡峭趨于平緩,對于鉆孔半徑0.5 mm工況,鉆孔對鋼絲應力的影響區域約為孔邊距5 mm范圍內,超過這一范圍幾乎沒有影響。

(2)通過對鉆孔半徑以及鉆孔深度進行參數影響規律分析,發現鋼絞線鋼絲鉆孔后孔邊應力釋放量隨鉆孔半徑及鉆孔深度的增加而增加。當鉆孔半徑一定時,對圓柱小孔理論上鉆孔深徑比達到2.0～3.0時孔邊應力釋放曲線趨于收斂。

(3)通過對鋼絞線進行大量鉆孔試驗驗證了仿真計算規律的可靠性,并通過測試結果與仿真模擬存在的差異,深入分析了圓柱形小孔和子彈頭狀小孔兩種不同鉆孔形狀差異對釋放收斂變化的影響,得出后者孔型時收斂深徑比取值更大,進一步為仿真模型修正和實際檢測數據處理提供了參考依據。

(4)通過對鉆孔半徑為0.5 mm,鉆孔深度為 2.5 mm 工況的實測數據進行擬合,得到了盲孔法試驗檢測時,鋼絞線有效預應力與孔邊2 mm測點處應變釋放量之間的函數關系,并考慮鉆孔偏差修正,經誤差分析得出,盲孔法識別鋼絞線有效預應力的擬合計算值與真實值之間相對誤差最大值為8.82%,且超過85%的數據相對誤差在7%以內。由此可以證明盲孔法識別計算鋼絞線有效預應力具有可行性。

盲孔法測試識別既有橋梁鋼絞線鋼絲應力作為一種新型的直接測試方法,最近已有檢測單位參考國外相關研究在實際工程中開展了探索性應用,但目前還未檢索到公開文獻進行實際工程檢測的相關報道。作為一種新型測試方法,仍有很多工作值得繼續深入研究。根據本文的研究,在采用盲孔法進行實際梁體有效預應力檢測時,應避開梁體控制截面,且選取靠近外側的管道進行測試,測試時需要對測試點附近很小范圍混凝土及壓漿漿體進行局部鑿除,且要避免造成對預應力筋的損傷,測試后再按相關規范要求進行混凝土修補。該法的不足是屬于一種局部破損的檢測方法,但是根據計算模擬分析有限的小盲孔對整根鋼絞線力學性能的影響微乎其微;其優點是一種直接測試方法,具有更高的檢測精度和檢測效率,可在一定條件下進行使用。由于鋼絞線硬度較高,需要專用高強合金鉆頭才能順利施鉆,專用自動化鉆孔設備也需要進一步研發。目前本文僅通過模擬試驗進行了相關驗證,尚未進行現場實際橋梁試驗,今后將通過實際橋梁檢測試驗進一步完善鋼絞線鋼絲盲孔應力釋放法的理論模型,積累數據,形成系統的檢測分析方法,為在役預應力混凝土鐵路橋梁有效預應力識別提供一種可行的直接檢測方法。