氯離子在混凝土中擴散效應分析的MCA模型

馬俊軍，藺鵬臻

(蘭州交通大學 土木工程學院，甘肅 蘭州 730070)

對于海洋等腐蝕性環境下的混凝土結構而言,由于氯離子侵蝕引起的鋼筋銹蝕是導致混凝土結構發生耐久性失效的主要原因[1-2]。研究氯離子在混凝土中的擴散機理和材料組分對混凝土中氯離子侵蝕擴散的影響規律將對海洋等腐蝕性環境下混凝土結構的耐久性設計、維修和加固具有重要意義[3]。

目前,物理試驗由于與實際情況最為接近,已成為國內外學者研究混凝土中氯離子擴散性能最常用的方法之一[4]。但由于試驗設備、場地、條件等因素的限制,使得試驗結果無法反映真實環境中結構的退化侵蝕現象[5]。而且試驗研究還存在周期長、成本高、試驗結果離散性大等問題。針對試驗方法的局限性,文獻[6-8]在Fick第二定律的基礎上,通過考慮不同的影響因素提出一系列用于描述混凝土中氯離子擴散過程的預測模型。雖然這些模型能夠很好地預測混凝土中氯離子的擴散行為,但都將混凝土看成一種宏觀勻質材料,且模型采用的理論公式比較簡單,只能考慮單一、確定性因素對氯離子擴散效應的影響,無法考慮材料組分和隨機分布對氯離子擴散效應的影響[9]。為此,文獻[10]從細觀角度出發,將混凝土看成由砂漿、界面過渡區(Interfacial Transition Zone,ITZ)、骨料組成的三相復合材料,并利用有限元法建立用于描述氯離子在混凝土中的細觀模型,并對混凝土氯離子擴散過程的影響因素進行分析。文獻[11]利用有限元法研究骨料對再生骨料混凝土中氯離子擴散特性的影響。文獻[12-13]將混凝土作為由砂漿和骨料組成的兩相復合材料,利用有限元法對混凝土中氯離子擴散行為進行分析。文獻[2,4]提出一種考慮材料非均質分布的細觀化等效方法,有效解決細觀材料的宏觀描述,提高模型的計算效率。但這些基于細觀尺度的混凝土氯離子擴散分析方法,由于網格尺寸的限制,無法考慮混凝土實際界面過渡區的尺寸,只適用于小尺度材料層面的研究,無法在整體結構中適用。

自文獻[14]用元胞自動機(Cellular Automata,CA)模擬氯離子在混凝土中的擴散過程以來,大量學者[3,15-16]利用元胞自動機對混凝土氯離子擴散過程進行研究。與有限元方法相比,該方法對網格尺寸沒有限制,可以根據需要隨意劃分網格。因此,結合細觀等效化方法和CA求解方法的優點,用來解決細觀模型在應用上的局限性。近來,文獻[3]采用細觀數值模擬方法,建立用于描述氯離子在混凝土中擴散行為的CA模型,并對元胞尺寸大小、時間步長等求解細節進行討論和優化。

在上述研究的基礎上,本文利用元胞自動機和細觀尺度模擬相結合的方法對混凝土中氯離子擴散行為進行研究。利用細觀尺度模擬方法建立考慮骨料等不均勻分布的混凝土隨機細觀模型。根據氯離子在混凝土中的實際擴散特點,推導基于細觀尺度的混凝土氯離子CA演變方程,建立基于細觀尺度的元胞自動機(Mesoscale Cellular Automata,MCA)模型。利用試驗結果對所提出的MCA模型的正確性和描述材料變異性的能力進行驗證。利用提出的模型對影響混凝土氯離子擴散特性的各個細觀結構參數進行分析。

1 混凝土細觀模型的建立

在細觀尺度上,可將混凝土看成由砂漿、界面過渡區(ITZ)、骨料組成的三相復合材料[17-18],由于骨料形狀基本不會對混凝土中氯離子擴散效應產生影響[13,19-20],因此本文骨料采用圓形。骨料粒徑范圍為4.75～31.50 mm,滿足Fuller級配曲線。基于蒙特卡洛(Monte-Carlo,MC)方法對生成的骨料顆粒進行隨機投放[18],建立考慮骨料等不均勻分布的混凝土隨機細觀模型,見圖1。圖1中,ITZ被模擬成介于骨料和砂漿之間的等厚度薄層,其厚度一般在20～100 μm之間[21],為簡化研究和提高計算效率,本文取ITZ厚度為50 μm。

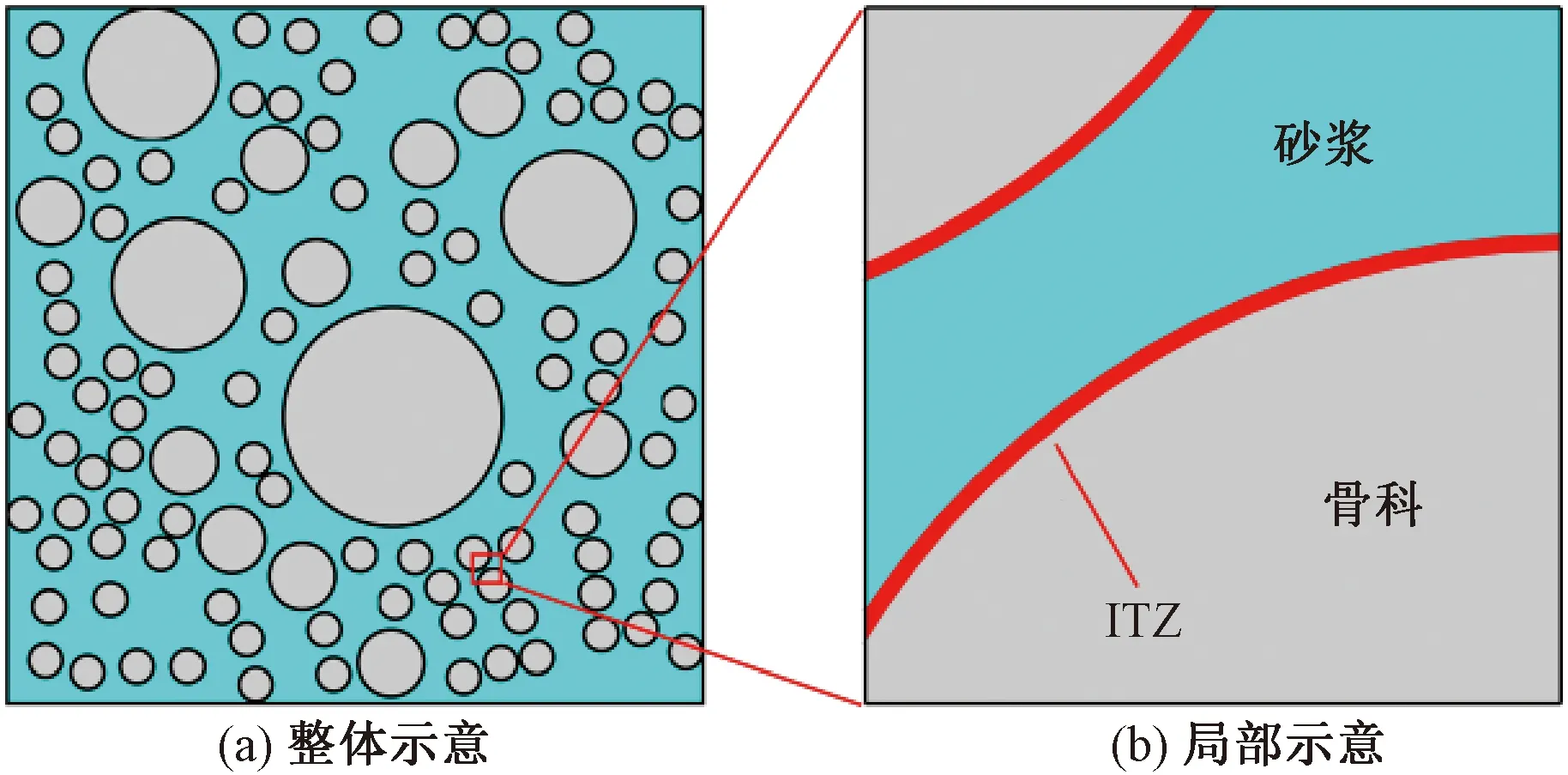
圖1 混凝土細觀模型示意

2 基于細觀尺度的混凝土氯離子擴散過程的元胞自動機表達

元胞自動機作為一種數值計算方法,可以用來求解氯離子在混凝土中的擴散行為。在已知元胞領域類型和局部進化規則的情況下,元胞自動機局部演化方程可描述為[14-15]

S(i,t+Δt)=f[S(1,t),…,S(i,t),…,S(n,t)]

( 1 )

式中:S(i,t+ Δt)為t+Δt時刻,元胞i的狀態;f為狀態轉移函數;n為元胞總數。

元胞C(i,j,k)各表面氯離子擴散通量示意見圖2。圖2中,t+ Δt時刻元胞C(i,j,k)中氯離子含量與t時刻元胞C(i,j,k)中氯離子含量和氯離子擴散通量之間的關系可描述為[3]

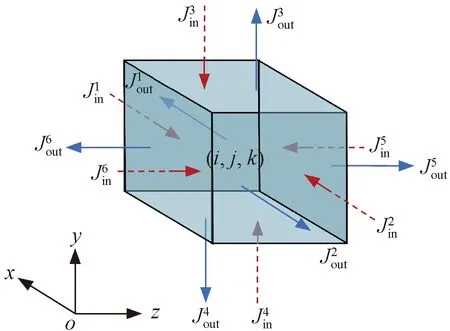
圖2 元胞C(i, j, k)各表面氯離子擴散通量示意

( 2 )

式中:C(i,j,k,t)、C(i,j,k,t+ Δt)分別為t、t+ Δt時刻單元(i,j)中氯離子含量:k為混凝土中氯離子擴散沿平面坐標的4個方向;Ak為兩元胞之間沿k方向氯離子擴散面的面積,m2;Jout為從元胞(i,j)流出的氯離子擴散通量;Jin為從元胞(i,j)流入的氯離子擴散通量。

二維元胞領域類型示意見圖3。

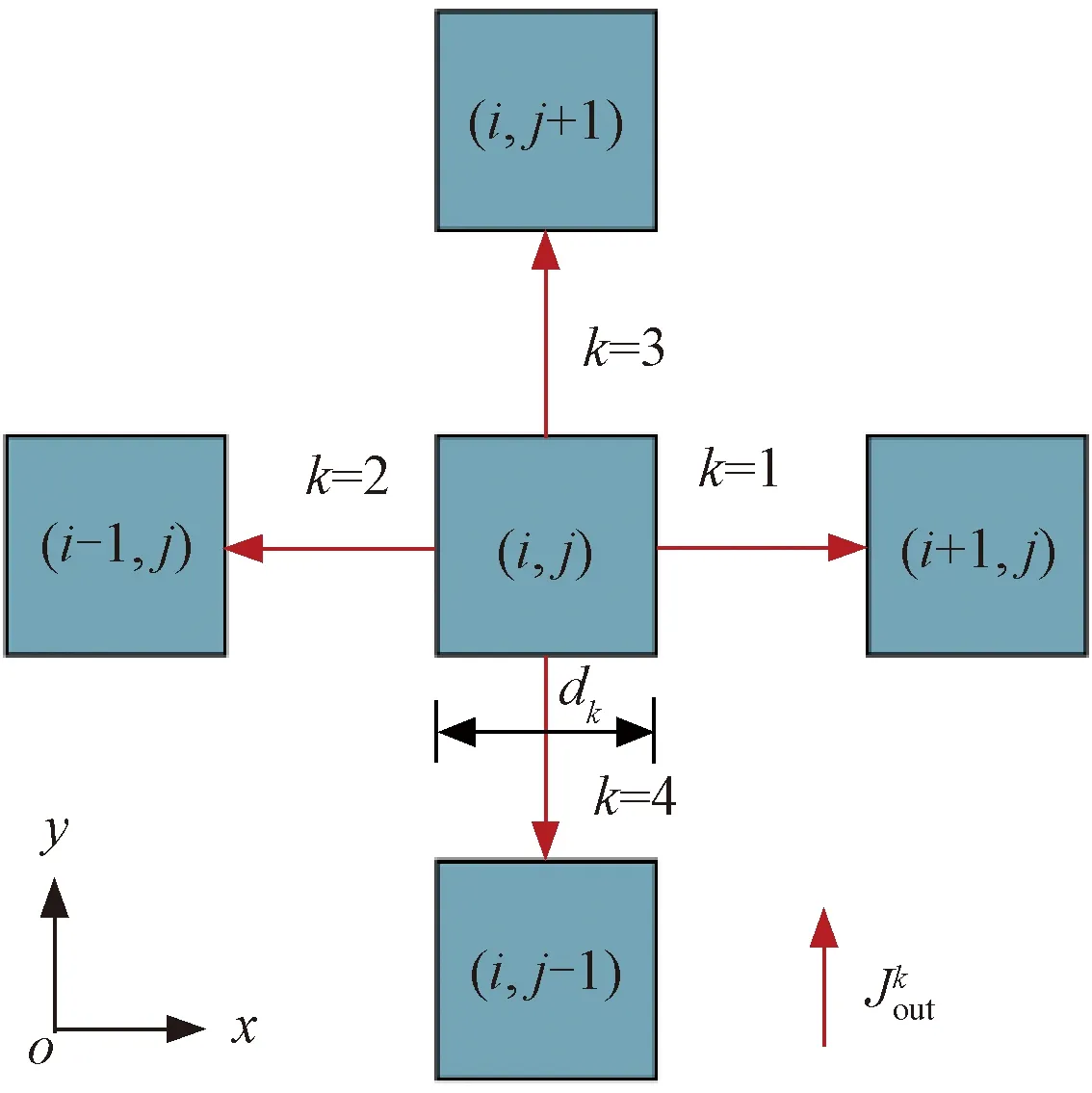
圖3 二維元胞領域類型示意

對于平面模型,根據式( 1 )、圖3,式( 2 )可進一步改寫為

( 3 )

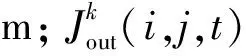
根據擴散第一定律,沿某一方向,氯離子擴散通量與其濃度成正比,即

( 4 )

式中:Dk(i,j)為元胞(i,j)沿k方向擴散到鄰居元胞(i+ik,j+jk)時的氯離子擴散系數,m2/s;c(i,j,t)為t時刻元胞(i,j)氯離子濃度值,%;δk為兩相鄰元胞之間的中心距離,m;當k=1～4時,ik、jk的取值分別為

( 5 )

結合式( 4 ),式( 3 )可以進一步描述為

( 6 )

當采用正方形元胞時,即dk=δk=δ。其中,δ為正方形元胞尺寸。式( 6 )可以簡化為

[c(i,j,t)-c(i+ik,j+jk,t)}

( 7 )

根據大數定理,元胞內氯離子含量與氯離子濃度成正比,即

C(i,j,k,t)=c(i,j,k,t)·Ae

( 8 )

式中:Ae為元胞內氯離子傳輸的有效面積。

此時,氯離子在混凝土中的擴散過程可以表達為

[c(i,j,t)-c(i+ik,j+jk,t)}

( 9 )

在不考慮骨料傳輸的情況下,即骨料中氯離子擴散系數DAgg=0,有效面積Ae可以表示為

Ae=(AMor+AITZ)δ2=(1-AAgg)δ2

(10)

式中:AMor、AITZ分別為元胞內砂漿、TTZ面積;AAgg為元胞內骨料所占的面積。

至此,式( 9 )可表達為

(11)

利用式(11)可建立混凝土中氯離子擴散過程的元胞自動機模型。

對于混凝土細觀模型而言,由于骨料和界面過渡區在空間上的隨機分布,使得元胞(i,j)沿任意方向表現出不同的侵蝕特性,主要體現在氯離子擴散系數Dk(i,j) 在各個方向上的取值具有隨機性。因此,為便于分析這種材料隨機性,本文提出一種細觀等效方法來模擬材料隨機性,以圖1中的混凝土細觀模型中的元胞(i,j)為例,其等效過程見圖4。主要分為以下幾個步驟:

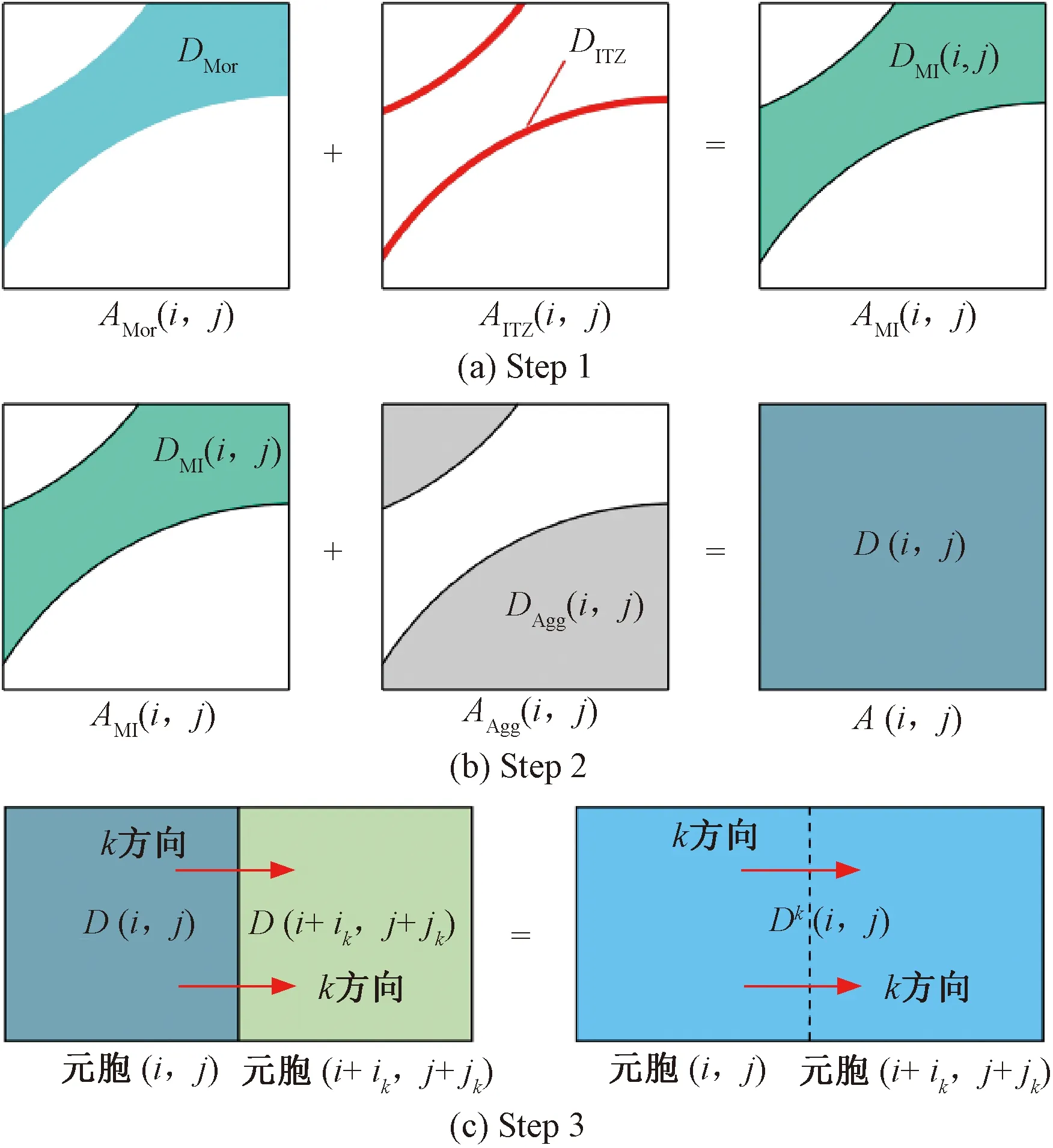
圖4 細觀模型等效過程示意

Step1根據元胞內砂漿、ITZ的面積分數,將元胞內砂漿、ITZ的氯離子擴散系數DMor(i,j)、DITZ(i,j)進行第一次均勻化等效,得到等效后氯離子擴散系數DMI(i,j)。

Step2根據元胞內骨料的面積分數,將Step1中等效后的氯離子擴散系數DMI(i,j)和骨料中氯離子擴散系數DAgg(i,j)進行第二次等效,得到等效后元胞氯離子擴散系數D(i,j)。

Step3根據元胞自動機局部演變規則,將上述得到的各元胞氯離子擴散系數D(i,j)沿著不同的擴散方向進行平均化處理,得到平均氯離子擴散系數Dk(i,j)。

由圖4可知,等效后各元胞的氯離子擴散系數D(i,j) 可以表示為各混凝土組成成分與其氯離子擴散系數的關系式,即

(12)

式中:AITZ(i,j)、AMor(i,j)、AAgg(i,j)分別為元胞(i,j)中界面過渡區、砂漿、骨料所占的面積分數,%;DAgg為骨料中氯離子擴散系數,一般取DAgg=0;DMor為砂漿中氯離子擴散系數;DITZ為ITZ中氯離子擴散系數,其與砂漿中氯離子擴散系數DITZ存在如下關系[21-22]

DITZ=αDMor

(13)

其中,α為ITZ與砂漿中氯離子擴散系數的比值,根據文獻[22],α和界面過渡區厚度tITZ之間的關系可以表示為

(14)

根據元胞內有效擴散系數D(i,j),Step3中各方向等效擴散系數Dk(i,j)表現出不同的等效結果,分別為:

(1)當D(i,j)=0或D(i+ik,j+jk)=0時,k方向擴散系數Dk(i,j)可以等效為

Dk(i,j)=0

(15)

(2)當D(i,j)≠0且D(i+ik,j+jk)≠0時,k方向擴散系數Dk(i,j) 可以等效為

(16)

3 氯離子擴散過程的時變效應

根據Thomas等[23]的試驗研究,發現混凝土中氯離子擴散系數隨時間t的關系可以用冪函數來表示,即

(17)

式中:DMor(t)為考慮侵蝕時間后的氯離子擴散系數,m2/s;D0為表觀氯離子擴散系數,m2/s;t0為混凝土參考齡期,一般取t0=28 d;m為時間依賴性參數。

4 計算流程

按照上述提出的混凝土隨機細觀模型和元胞自動機模擬方法,利用Matlab軟件編寫混凝土氯離子擴散效應分析的細觀元胞自動機模型計算程序,具體流程見圖5。圖5中,Ncell為元胞總個數。

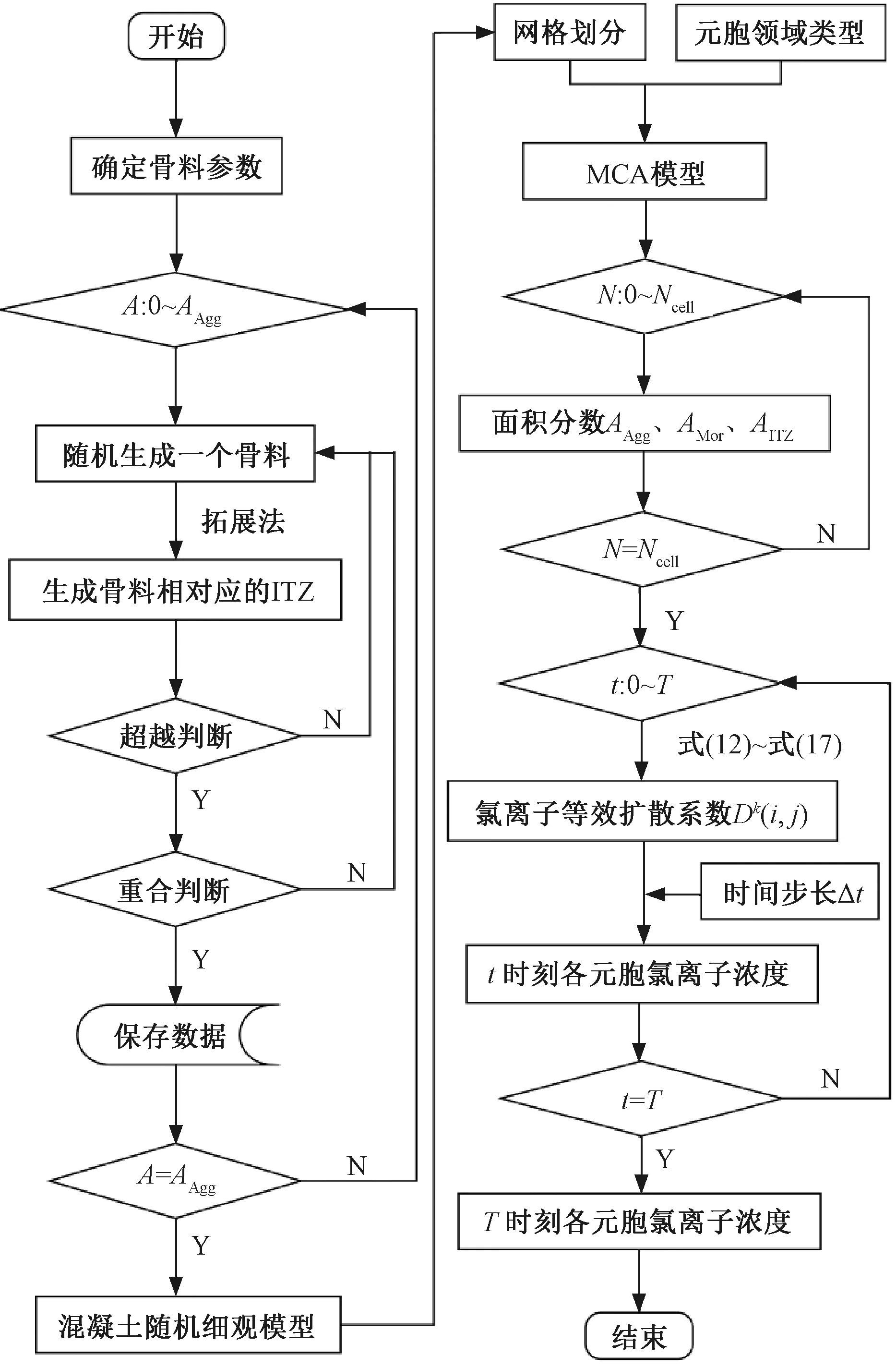
圖5 混凝土氯離子擴散效應分析流程示意

5 元胞尺寸確定方法

從上述等效過程可知,元胞尺寸太大,模型無法真實反映骨料在截面內的實際分布,造成模擬值與實際結果的偏差。元胞尺寸太小,不利于混凝土細觀參數的統計與提取,也降低了計算效率。根據式(10),在采用圓形骨料的情況下,為使建立的MCA模型能真實反映骨料在截面內的實際分布,理論上元胞尺寸應滿足如下關系

(18)

式中:δe、δmax分別為模型計算、最大理論尺寸,當δe=δmax時,模型計算結果最準確、高效,當采用尺寸δe無法進行網格劃分時,可取δe<δmax,但為保證精度,取值不易太小;dmin為骨料最小粒徑,m。

為驗證式(18)確定的元胞尺寸是否合理。以圖1中的混凝土細觀模型為例,考慮混凝土實際尺寸和元胞類型,同時為便于網格劃分,利用數值試驗,分別比較δ=1、2、4、5 mm時MCA模型的模擬結果。模擬歷經480 d后混凝土截面氯離子濃度的分布情況,選擇距離混凝土表面不同深度氯離子濃度模擬值的平均值作為評價指標,比較結果見圖6。同時,為便于比較,圖中還給出了宏觀尺度下Fick第二定律的解析解。

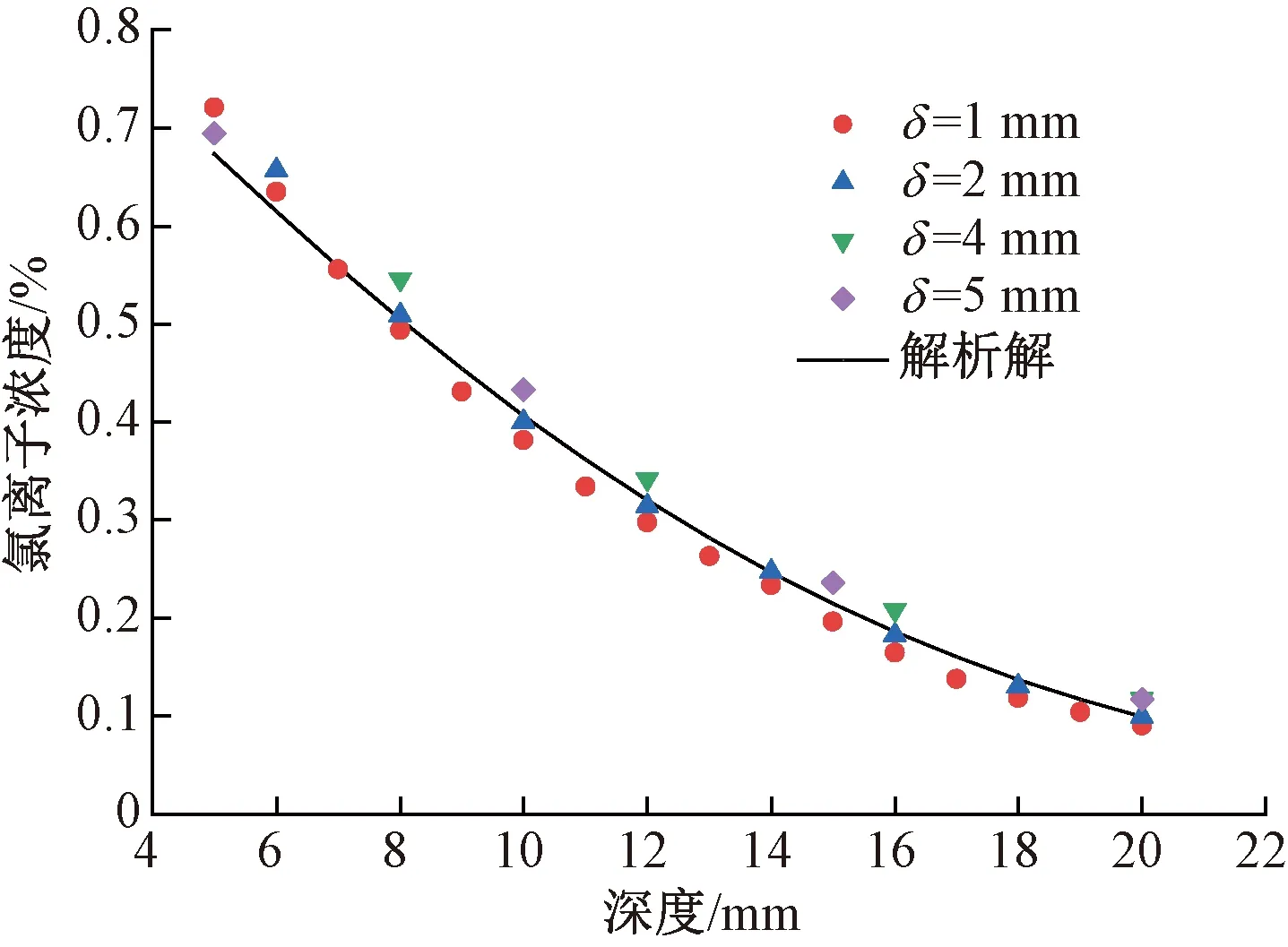
圖6 不同元胞尺寸下MCA模型的模擬結果與解析解的比較

由圖6可知,不同網格尺寸下,截面氯離子濃度模擬值隨深度的變化規律與解析解隨深度的變化規律一致。當δ=2 mm(最接近δmax=3.4 mm)時,模型模擬值與解析解之間偏差最小。當元胞尺寸太小(δ=1 mm),模型將低估氯離子在混凝土中的擴散行為。當δ>δmax,即δ=4、5 mm,模型將高估氯離子在混凝土中的擴散行為。這說明MCA模型元胞尺寸確定方法是合理的。對于常規混凝土而言,為使MCA模型計算結果高效、準確,推薦采用δ=0.707dmin。

6 數值模擬與試驗驗證

6.1 MCA模型的建立

為驗證MCA模型的準確性,對文獻[24]中強度等級為C30的混凝土受氯離子侵蝕試驗過程進行數值模擬,將模型模擬結果與試驗結果進行比較。根據混凝土細觀尺度模擬方法,建立截面尺寸為100 mm×100 mm的混凝土細觀模型,見圖1。圖1中,骨料面積分數(AAgg=40%)和粒徑分布(4.75～31.50 mm)與文獻[24]相同。為便于與試驗結果進行對比,根據第4節的研究結果,在保證計算精度的情況下,δ=2 mm,劃分后的混凝土隨機細觀模型見圖7。

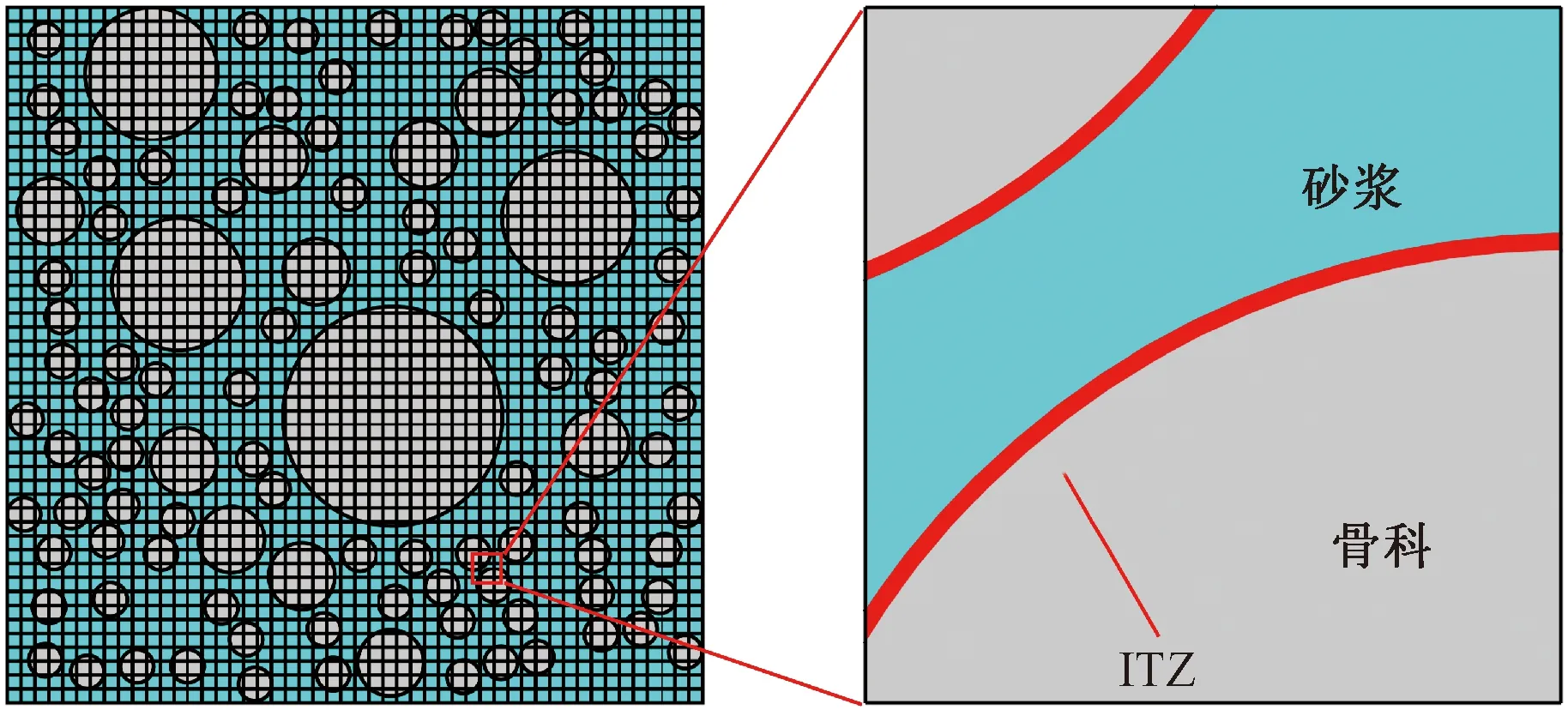
圖7 混凝土細觀模型網格劃分示意

在混凝土細觀模型等效時,D0=3.931×10-12m2/s,m=0.608 3,t=480 d,混凝土界面擴散特性參數利用式(14)確定,等效后各元胞等效氯離子擴散系數見圖8。由圖8可知,等效后截面各位置氯離子擴散系數不再是常數,而是隨骨料等組成成分的變化而變化。通過與圖1對比,發現顏色越接近紅色代表元胞內砂漿的面積分數越高,等效后D0越大;顏色越接近藍色代表元胞內AITZ越高,等效后D0越小。說明提出的氯離子擴散系數等效方法可以模擬混凝土中骨料和ITZ隨機分布對D0的影響。

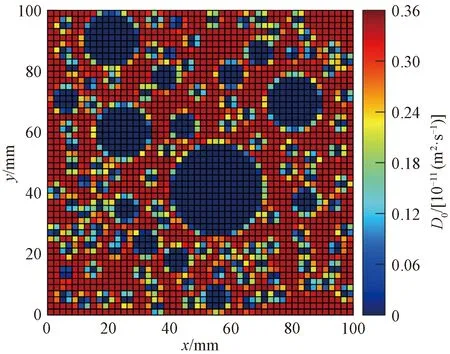
圖8 等效氯離子擴散系數分布

6.2 氯離子濃度驗證

為驗證MCA模型的準確性,將模型的模擬結果與文獻[24]中試驗結果進行比較。由于基于化學滴定法得到的氯離子濃度實測值代表的是截面氯離子濃度分布的平均結果,因此為便于與試驗結果進行比較,選擇距離混凝土表面同一深度氯離子濃度模擬值的平均值作為評價指標。模型計算參數分別為:D0=3.931×10-12m2/s,實際氯離子擴散系數根據式(12)～式(16)確定,m=0.608 3,Δt=0.1 d,δ=2 mm。不同侵蝕時間后截面平均氯離子濃度模擬值和試驗實測值隨深度h、時間的變化曲線見圖9。

由圖9可知,模型的模擬結果與試驗值隨侵蝕深度和時間的變化趨勢一致,均隨侵蝕深度的增加而減小,隨侵蝕時間的增加而增加。表明利用MCA模型預測的氯離子濃度隨侵蝕深度和時間的變化規律與試驗結果一致。

隨后,將MCA模型預測的截面氯離子濃度模擬值與文獻[24]中實測值進行對比,對比結果見圖10。由圖10可知,除少數氯離子濃度模擬值與實測值之間的偏差在35%以內,所有采用MCA模型模擬的截面氯離子濃度模擬值與實測結果之間的偏差都在±10%以內。說明提出的模型可以用于模擬氯離子在混凝土中的擴散過程,且精度較高,這也可以通過圖6中模型模擬值與解析解的偏差得出。通過與文獻[24]對比,發現造成極少數氯離子濃度模擬值與試驗值偏差的主要原因是模型采用的氯離子擴散系數是文獻[24]通過試驗數據擬合后的結果,而文獻[24]中的試驗數據來自不同的試驗環境,試驗數據的采集也來自不同測試人員,使得各試驗數據之間本身存在一定的誤差。

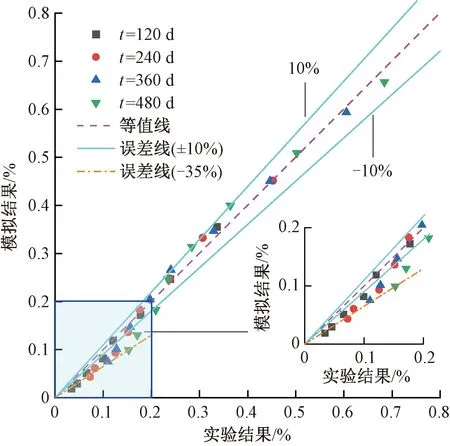
圖10 氯離子濃度實測值與模擬值的對比

6.3 空間變異性驗證

與傳統有限元細觀模型相比,MCA模型除能準確描述混凝土截面平均氯離子濃度隨時間和深度的變化外,還應能描述材料變異特性,如骨料尺寸大小、空間不均勻分布等對氯離子擴散行為的影響。為此,在上述分析的基礎上,利用MCA模型給出不同侵蝕時間后截面氯離子濃度分布示意,見圖11。

由圖11可知,在同一侵蝕時刻,距離混凝土表面同一深度氯離子濃度值各不相同,在砂漿分布區域(顏色越接近紅色區域),元胞代表的氯離子濃度最大,在骨料分布區域(顏色越接近藍色區域),元胞代表的氯離子濃度最小,這與氯離子在混凝土中的實際擴散行為相符,即氯離子擴散行為僅發生在砂漿區域,而不考慮骨料的滲透性。說明提出的氯離子擴散系數等效方法是合理的,也證明模型具有描述材料變異特性的能力。

在應用方面,由于MCA模型在求解過程中不需要求解高階微分方程,因此可模擬任意復雜結構中氯離子的擴散行為。利用MCA模型,可以使工程設計人員直觀了解混凝土截面內最容易引起鋼筋銹蝕的薄弱位置,進而對結構的耐久性設計、壽命預測、維修和加固等提供一定的理論依據。

此外,從計算效率來看,當δ=2 mm時,MCA模型所需的元胞數量僅為50個,遠遠小于傳統有限元細觀模型所需的單元數[2],相比而言,MCA模型大大提高了模型的計算效率。

7 參數分析

在上述對模型的準確性進行驗證的情況下,利用MCA模型進行敏感性分析,以驗證骨料分布形式、骨料含量、界面擴散特性等細觀結構參數對氯離子擴散效應的影響。純砂漿截面見圖12(a)。為便于討論,將純砂漿截面中氯離子濃度值作為參考,以此來驗證各細觀參數對氯離子宏觀擴散特性的影響程度。同時為反映各細觀結構參數對氯離子擴散的影響規律,引入截面有效氯離子擴散系數平均值Da,其表達式為

圖12 不同骨料分布形式的混凝土細觀模型和砂漿模型示意

(19)

式中:D(i,j)為各元胞的氯離子擴散系數,m2/s;m、n分別為截面內元胞的行數、列數。

7.1 骨料分布形式

為研究骨料分布形式對混凝土氯離子擴散效應的影響,考慮骨料在混凝土中的隨機分布,建立5種不同骨料分布形式的混凝土細觀模型,見圖12(b)～圖12(f),截面尺寸為100 mm×100 mm。利用MCA模型對5種不同骨料分布形式下混凝土中氯離子擴散過程進行數值模擬,計算參數分別取:Δt=0.1 d,t=480 d,m=0.608 3,D0=3.931×10-12m2/s,實際氯離子擴散系數根據式(12)～式(16)確定,AAgg=0.4,tITZ=50 μm,δ= 2 mm。

截面有效氯離子擴散系數平均值Da隨骨料分布形式的變化關系見圖13。由圖13可知,不同骨料分布形式下Da基本保持不變。說明骨料分布形式基本不會對混凝土中氯離子宏觀分布規律產生影響。

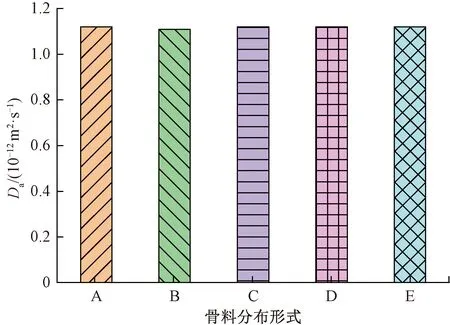
圖13 Da隨骨料分布形式的變化關系

同時,為便于同其他細觀參數比較,選擇距離混凝土表面同一深度氯離子濃度平均值作為評價指標。不同骨料分布形式下截面氯離子濃度模擬值與參考值的比較結果見圖14。由圖14可知,截面各模擬值與參考值之間最大偏差不超過12%。說明在一定誤差范圍內,可認為骨料分布形式基本不會對截面氯離子濃度分布規律產生影響,這與圖13得出的結論一致。

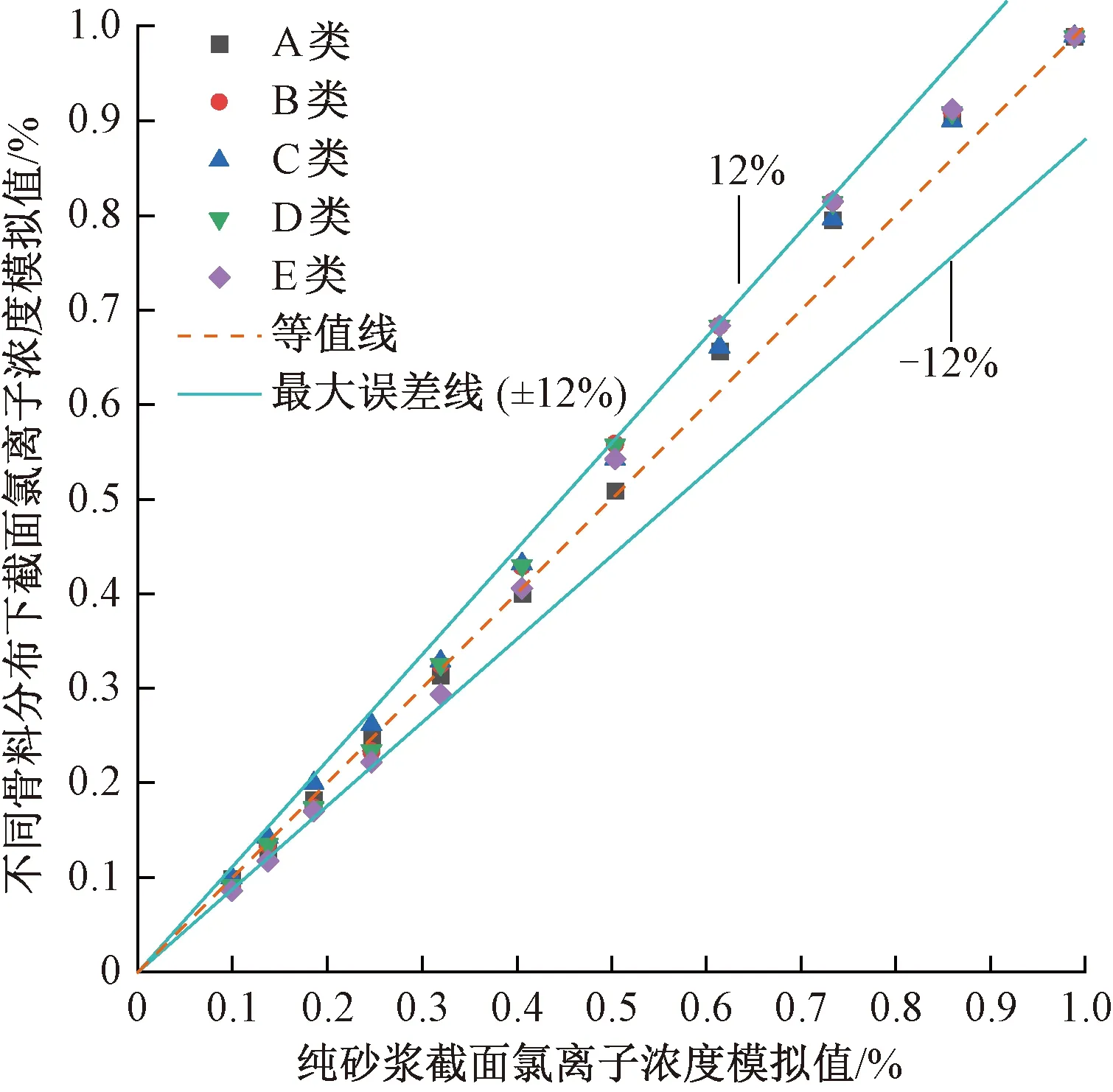
圖14 不同骨料分布形式下截面內氯離子濃度模擬值與參考值的比較結果

7.2 骨料含量

為研究骨料含量對氯離子宏觀擴散效應的影響,對5種不同骨料含量下混凝土中氯離子侵蝕過程進行模擬,除AAgg外,各計算參數、模型尺寸均與上述模型保持一致。截面有效氯離子擴散系數平均值Da隨骨料含量AAgg的變化曲線見圖15。

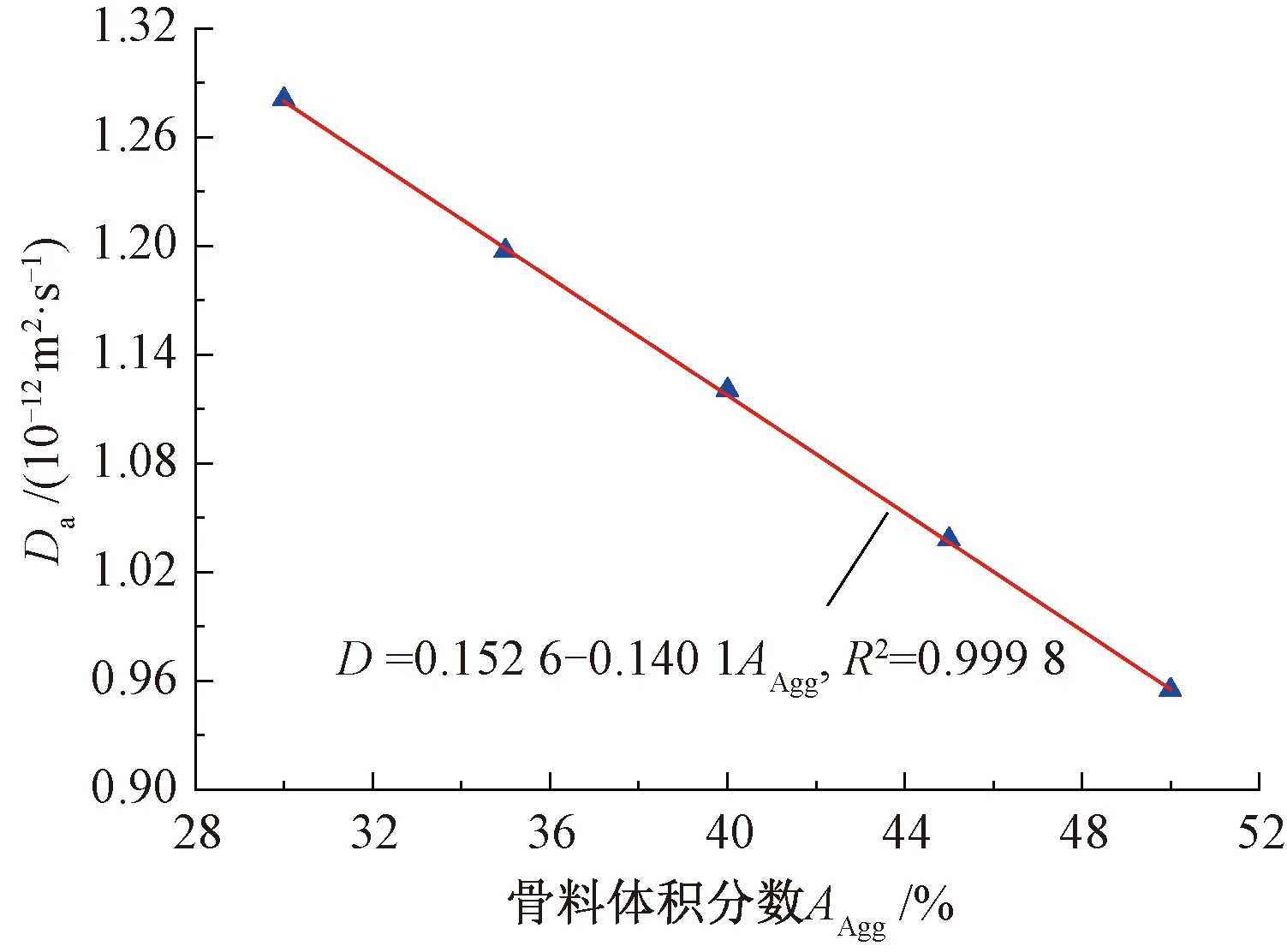
圖15 Da隨AAgg的變化曲線

由圖15可知,隨著骨料含量的增加,Da呈現出線性減小的變化規律。結果表明,隨著AAgg的增加,氯離子在混凝土中的宏觀擴散特性逐漸減弱,增加混凝土中骨料的含量可以抑制氯離子在混凝土中的擴散行為。同時,為便于同其他細觀結構參數進行比較,選擇距離混凝土表面同一深度氯離子濃度模擬值的平均值作為評價指標,將上述氯離子濃度模擬值與其平均值進行對比,見圖16。

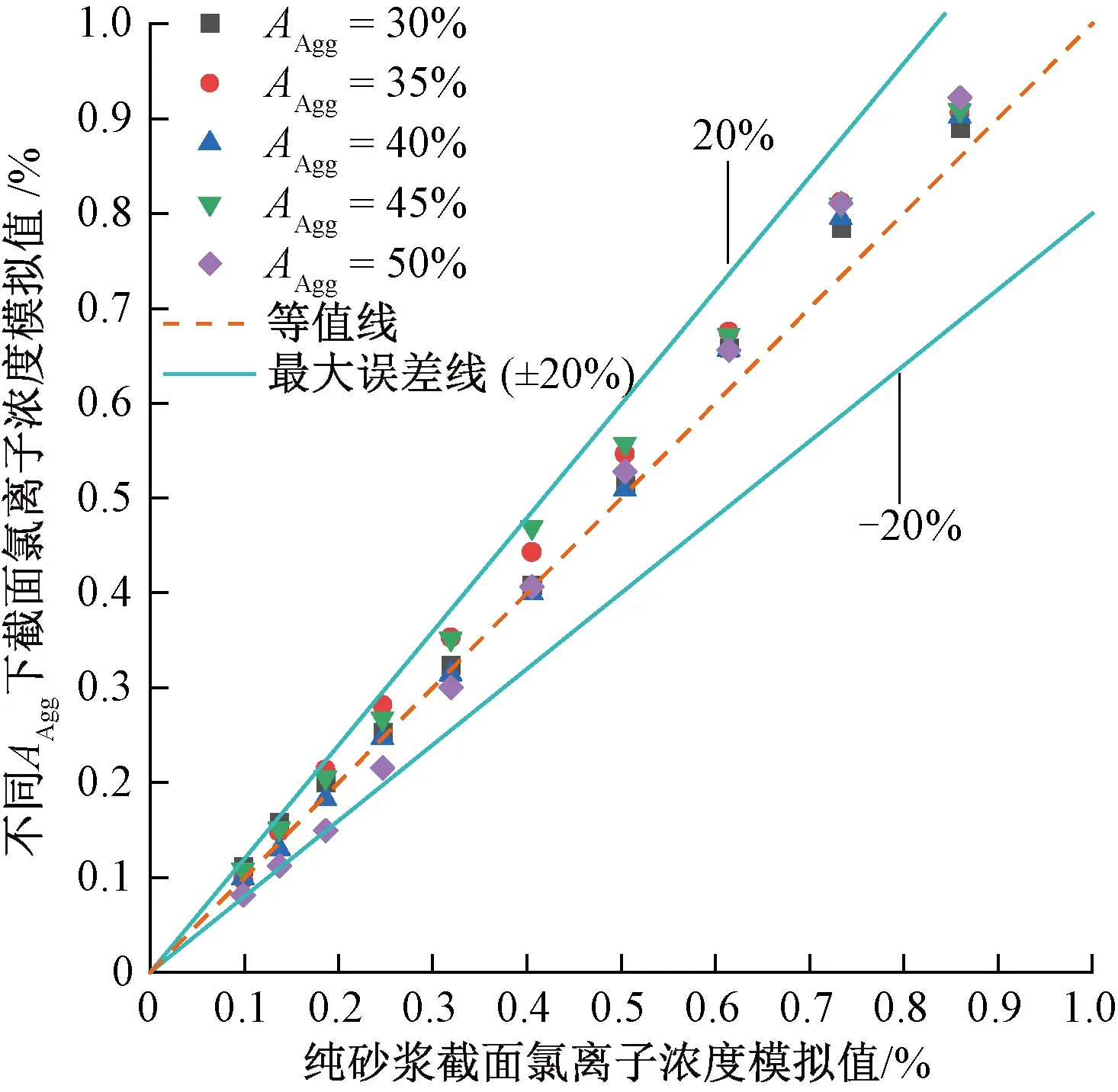
圖16 不同AAgg下截面內氯離子濃度模擬值與參考值的比較

由圖16可知,截面各位置氯離子濃度模擬值與參考值之間最大誤差為20%,截面各位置氯離子濃度模擬值與參考值之間的偏差隨氯離子濃度值的增加而減小。

7.3 界面擴散特性

ITZ作為連接骨料和砂漿的重要組成成分,是混凝土中最為薄弱的部位,也是影響混凝土結構力學性能和耐久性的主要因素。因此,為研究混凝土界面擴散特性對氯離子擴散效應的影響,對8種不同α(DITZ/DMor)下混凝土中氯離子侵蝕過程進行模擬。除α外,各計算參數、模型尺寸均與上述模型保持一致。截面有效氯離子擴散系數平均值Da隨α的變化曲線見圖17。

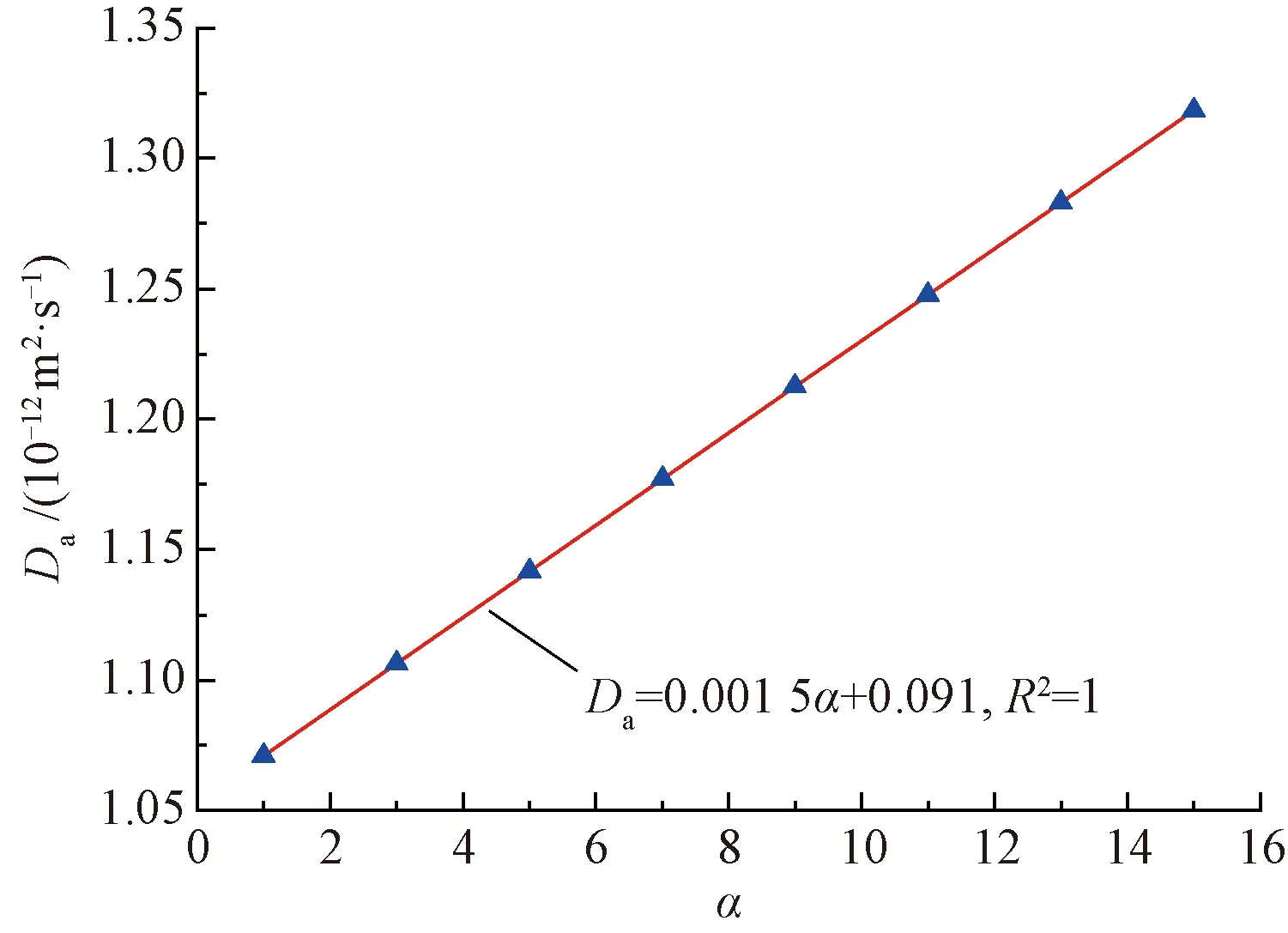
圖17 Da隨 α的變化曲線

由圖17可知,Da隨α的增加呈現出線性增加的變化規律。結果表明,隨著α的增加,氯離子在混凝土中的宏觀擴散特性逐漸增強。

同時,為便于同其他參數進行對比,選擇距離混凝土表面同一深度氯離子濃度平均值作為評價指標,將上述不同α下截面氯離子濃度模擬值與參考值進行比較,結果見圖18。

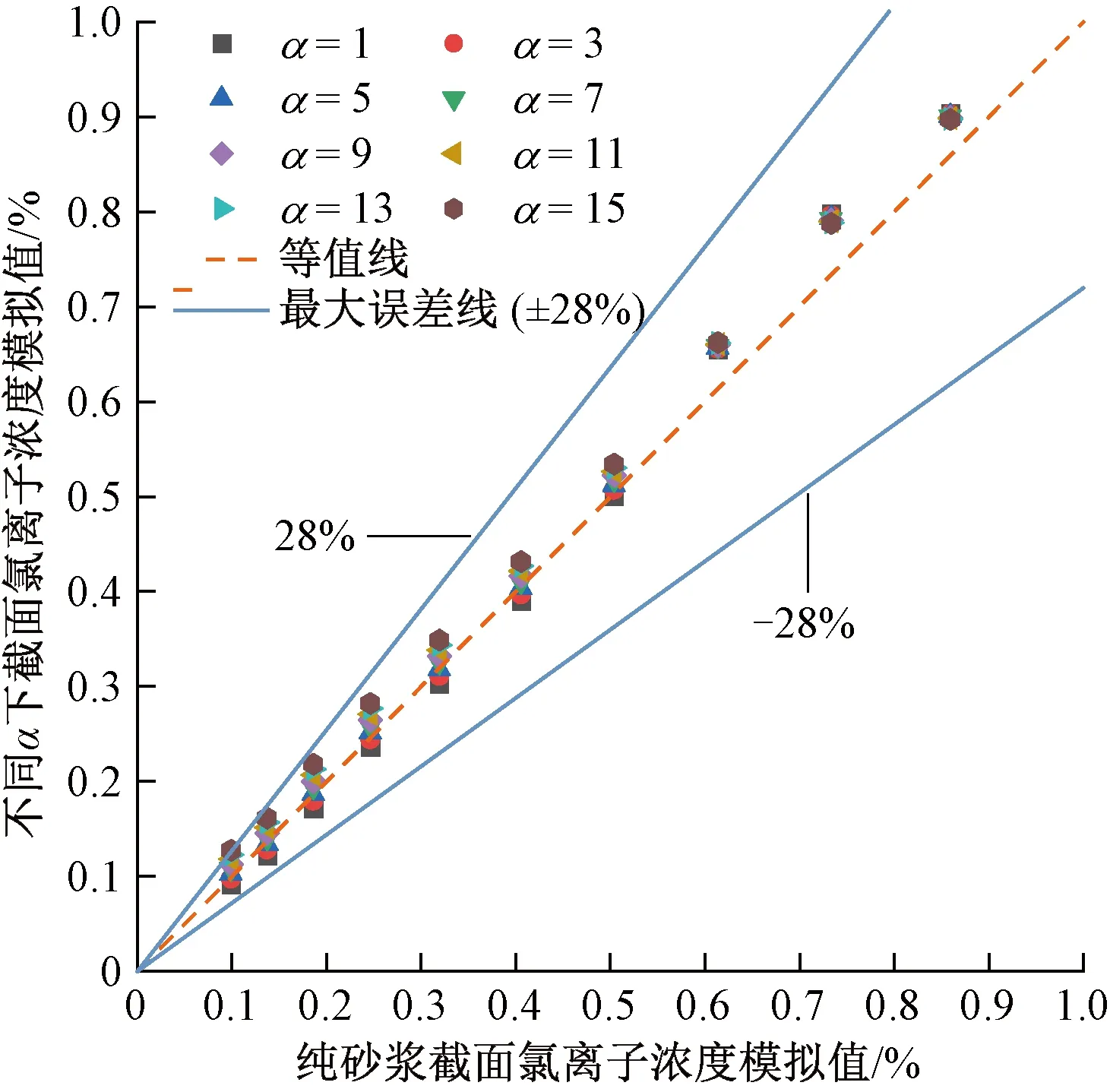
圖18 不同α下截面內氯離子濃度模擬值與參考值的對比結果

由圖18可知,不同α下截面氯離子濃度模擬值之間的差值隨氯離子濃度的減小而增加。當α=15時,兩者之間偏差最大,為28%。可見α的取值對氯離子在混凝土中的宏觀擴散特性存在很大的影響,在氯離子擴散效應分析時,合理選擇α值將直接關乎結果的正確與否。

綜上所述,通過對比不同參數下截面中氯離子濃度模擬值與參考值之間的偏差,發現界面擴散特性對細觀混凝土中氯離子的宏觀擴散特性影響最顯著,兩者之間偏差最大,為28%,體積分數對細觀混凝土中氯離子的宏觀擴散特性影響較為顯著,兩者之間偏差為20%,而骨料分布形式則基本不會對混凝土氯離子擴散效應產生影響,兩者之間偏差最小,僅為14%,這與既有研究結果規律一致[13,19-20]。

8 結論

本文基于細觀尺度模擬方法,將混凝土看成由砂漿、界面過渡區和骨料組成的三相復合材料,建立相應的隨機細觀模型,提出考慮氯離子時變擴散效應的MCA模型。利用試驗實測數據和理論解對模型進行驗證,并在此基礎上利用模型進行敏感性分析。最后得出以下結論:

(1)根據混凝土組成特點,將混凝土看成由砂漿、ITZ、骨料組成的三相復合材料,基于MC方法建立考慮骨料等不均勻分布的混凝土隨機細觀模型。并在此基礎上,結合元胞自動機理論,提出一種均勻化等效方法,建立用于描述氯離子在混凝土中擴散行為的MCA模型。

(2)利用模型對影響模型計算效率和應用限制的元胞尺寸大小進行討論,為保證計算精度和準確反映氯離子在各相組成材料中的擴散特性,推薦采用δ= 0.707dmin。 與傳統有限元細觀模型相比,提出的模型有效解決了有限元模型由于網格尺寸限制而無法考慮實際界面過渡區尺寸和計算效率低的難題。

(3)通過與實驗結果和理論解的比較,驗證MCA模型的準確性和描述材料變異特性的能力。模型能夠反映混凝土細觀組成材料(如砂漿、骨料、ITZ)中氯離子的實際擴散特性。提出的方法為細觀結構和宏觀模型之間建立了橋梁,這對進一步整體截面或結構分析具有重要意義。

(4)參數化分析結果表明,界面擴散特性對細觀混凝土中氯離子的宏觀擴散特性影響最顯著,體積分數對細觀混凝土中氯離子的宏觀擴散特性影響較為顯著,而骨料分布形式基本不會對氯離子擴散效應產生影響。總體規律是氯離子擴散效應隨界面擴散特性的增加而增加,隨骨料體積分數的增加而減小。