32 m簡(jiǎn)支梁橋有砟軌道精搗上拱誤差模型及其修正研究

江來(lái)偉，岑敏儀，張同剛，李陽(yáng)騰龍

(1.西南交通大學(xué) 地球科學(xué)與環(huán)境工程學(xué)院，四川 成都 611756；2.西南交通大學(xué) 土木工程學(xué)院，四川 成都 610031；3.成都理工大學(xué) 地球科學(xué)學(xué)院，四川 成都 610059)

軌道不平順為軌道-車輛系統(tǒng)的激擾源,造成極大的機(jī)車車輛振動(dòng)和輪軌作用力,對(duì)行車的安全性、舒適性、平穩(wěn)性、機(jī)車車輛和軌道組件壽命以及環(huán)境噪聲均產(chǎn)生很大影響[1-2]。張曙光等[3]對(duì)京津城際軌道平順性研究時(shí)發(fā)現(xiàn)存在周期為33 m的高低不平順,建議對(duì)周期性不平順成因和控制方法進(jìn)行深入研究。宋國(guó)華等[4]對(duì)秦沈線月牙河特大橋進(jìn)行動(dòng)力和軌道不平順?lè)治?認(rèn)為橋上有砟軌道周期性高低不平順并非由動(dòng)荷載下橋梁撓度變形引起,根本原因是橋梁徐變引發(fā)上拱造成。陳憲麥等[5]對(duì)京滬、滬杭、滬寧等高速鐵路軌道不平順的研究表明,軌道高低普遍存在24～25 m、32～33 m不利波長(zhǎng)范圍的周期性不平順。康熊等[6]分析高速鐵路無(wú)砟軌道不平順譜特征時(shí)發(fā)現(xiàn),多等跨簡(jiǎn)支梁存在波長(zhǎng)等于簡(jiǎn)支梁跨度的周期性不平順。田國(guó)英[7]利用不平順數(shù)據(jù)計(jì)算高速鐵路軌道平均譜時(shí)指出,高低不平順譜中包含大量的與橋梁跨距一致的波長(zhǎng)成分。楊飛等[8]研究成灌城際鐵路橋上動(dòng)態(tài)檢測(cè)高低數(shù)據(jù)時(shí)發(fā)現(xiàn),存在周期性不平順,認(rèn)為混凝土的收縮、徐變以及橋梁剛度偏弱是主要原因,并指出32 m波長(zhǎng)周期性不平順落在列車160、200 km/h的敏感波長(zhǎng)范圍內(nèi)。具有連續(xù)布置的多等跨簡(jiǎn)支梁橋的周期性變形,將改變軌道的幾何狀態(tài),對(duì)列車的行車安全和乘坐舒適性均是有害的[9]。已有研究成果多針對(duì)無(wú)砟軌道動(dòng)態(tài)檢測(cè)高低不平順進(jìn)行分析,指出梁體上拱造成軌道高低周期性不平順,并認(rèn)為上拱是受混凝土徐變影響所致,但未就上拱數(shù)學(xué)表現(xiàn)形式及精測(cè)精調(diào)作業(yè)中如何科學(xué)地控制做進(jìn)一步研究。目前橋梁有砟軌道精測(cè)精搗后普遍存在上拱問(wèn)題,與無(wú)砟軌道相比,有砟軌道上拱機(jī)理研究較少。隨著250 km/h有砟軌道運(yùn)營(yíng)線路越來(lái)越多,橋梁占比和大跨連續(xù)布置的多跨簡(jiǎn)支梁橋不斷增加,為確保列車在有砟軌道橋梁段安全平穩(wěn)地高速行駛,探究橋梁有砟軌道上拱成因和解決辦法已迫在眉睫。

1 簡(jiǎn)支梁橋軌道垂向不平順的動(dòng)靜態(tài)特性

軌道幾何狀態(tài)檢測(cè)有靜態(tài)檢測(cè)(主要設(shè)備為各類軌測(cè)儀、電子水準(zhǔn)儀等)和動(dòng)態(tài)檢測(cè)(主要設(shè)備為軌檢車、動(dòng)檢車、綜合檢測(cè)列車等)。就垂向而言,靜態(tài)檢測(cè)獲取軌道實(shí)測(cè)高程和設(shè)計(jì)高程,由二者代數(shù)差確定軌道垂向偏差,并可由此計(jì)算不同弦長(zhǎng)的軌道高低[10]。動(dòng)態(tài)檢測(cè)是將軌道縱斷面軌跡通過(guò)數(shù)字濾波運(yùn)算,獲得不同波長(zhǎng)范圍內(nèi)的軌道高低。垂向偏差或不同波(弦)長(zhǎng)高低用于描述軌道垂向不平順。

已有研究表明[11],軌道長(zhǎng)波不平順可致使列車晃動(dòng)、車體平穩(wěn)性惡化、軌道形位劣化加速和車輛-軌道部件損傷。在高速條件下,軌道長(zhǎng)波不平順激勵(lì)甚至?xí)l(fā)共振[12],威脅行車安全。以160 km/h為例,列車行駛時(shí)軌道高低的共振波長(zhǎng)范圍為31.4～62.8 m。若該波長(zhǎng)范圍內(nèi)不平順?lè)递^大,極易引起車體共振、車體平穩(wěn)性惡化,故此需對(duì)30～70 m波長(zhǎng)范圍軌道高低不平順進(jìn)行合理控制[13-14]。

1.1 五種線下工程軌道高低不平順譜

功率譜密度(Power Spectral Density,PSD)函數(shù)作為表征軌道不平順的統(tǒng)計(jì)函數(shù),能揭示隨機(jī)變化的軌道不平順?lè)岛筒ㄩL(zhǎng)兩方面信息[11,14]。某設(shè)計(jì)速度160 km/h(預(yù)留200 km/h)電氣化新建快速有砟鐵路(部分隧道為無(wú)砟),統(tǒng)計(jì)里程K72+900—K220+900(上下行約296 km)范圍內(nèi),聯(lián)調(diào)聯(lián)試80～160 km/h五種檢測(cè)速度動(dòng)態(tài)檢測(cè)70 m截止波長(zhǎng)軌道高低。按隧道洞口有砟軌道和無(wú)砟軌道過(guò)渡段,路基有砟軌道段,32 m簡(jiǎn)支梁橋(梁體為后張法預(yù)應(yīng)力混凝土梁,下文相同)有砟軌道段,隧道有砟軌道和隧道無(wú)砟軌道段等五種線下工程區(qū)分。分別計(jì)算軌道高低平均不平順譜,見(jiàn)圖1。

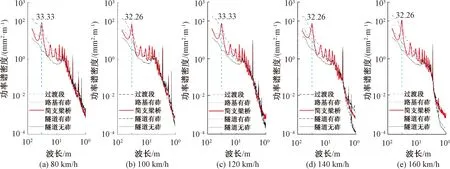
圖1 五種線下工程軌道高低不平順譜

不同速度等級(jí)下五種線下工程的軌道高低不平順譜,其趨勢(shì)基本保持一致,波長(zhǎng)越長(zhǎng),高低不平順?lè)翟酱蟆５档米⒁獾氖?32 m簡(jiǎn)支梁橋與其他線下工程存在顯著差異,在波長(zhǎng)3 m以上存在多個(gè)譜峰。其中,峰值處對(duì)應(yīng)基頻波,波長(zhǎng)為32.26～33.33 m,這與32 m簡(jiǎn)支梁橋跨距基本吻合,其他譜峰多為倍頻成分。不同線下工程的軌道高低不平順譜表明,聯(lián)調(diào)聯(lián)試期間,32 m簡(jiǎn)支梁橋有砟軌道仍舊存在大量且波長(zhǎng)單一的高低不平順。

1.2 精搗前后軌道垂向不平順的靜態(tài)特性

有砟軌道的幾何形位,主要由搗固車的精確搗固作業(yè)(以下簡(jiǎn)稱精搗)來(lái)控制。精搗是依據(jù)靜態(tài)檢測(cè)橫垂向偏差(精測(cè))制定的精搗方案指導(dǎo)搗固車起/撥道抄平來(lái)實(shí)現(xiàn)的。受作業(yè)殘余誤差以及道床彈性不均的影響,有砟軌道精搗難以一次性完成。實(shí)際中采取“精測(cè)—精搗(穩(wěn))—精測(cè)”的重復(fù)作業(yè)模式(新建有砟鐵路通常需3～4次精搗作業(yè))[15],至各項(xiàng)指標(biāo)符合靜態(tài)驗(yàn)收標(biāo)準(zhǔn)后,實(shí)施聯(lián)調(diào)聯(lián)試作業(yè)。某新建有砟鐵路由GPS/INS組合導(dǎo)航軌道快速檢測(cè)系統(tǒng)配合DWL-48K型搗固車搗穩(wěn)聯(lián)合重復(fù)作業(yè),搗固模式為三點(diǎn)式精搗。選取六座采用32 m后張法預(yù)應(yīng)力混凝土梁布置的簡(jiǎn)支梁橋(a～f),最后三次(n-2、n-1、n)精搗后軌道靜態(tài)檢測(cè)垂向偏差(已做零均值化處理),得其波形見(jiàn)圖2,n表示精搗作業(yè)的次數(shù)。計(jì)算3種弦長(zhǎng)(10、30、70 m)的軌道高低不平順,取200 m作為單元區(qū)段,統(tǒng)計(jì)最后兩次精搗前后橋梁a～f區(qū)段平均標(biāo)準(zhǔn)差的變化,見(jiàn)圖3。

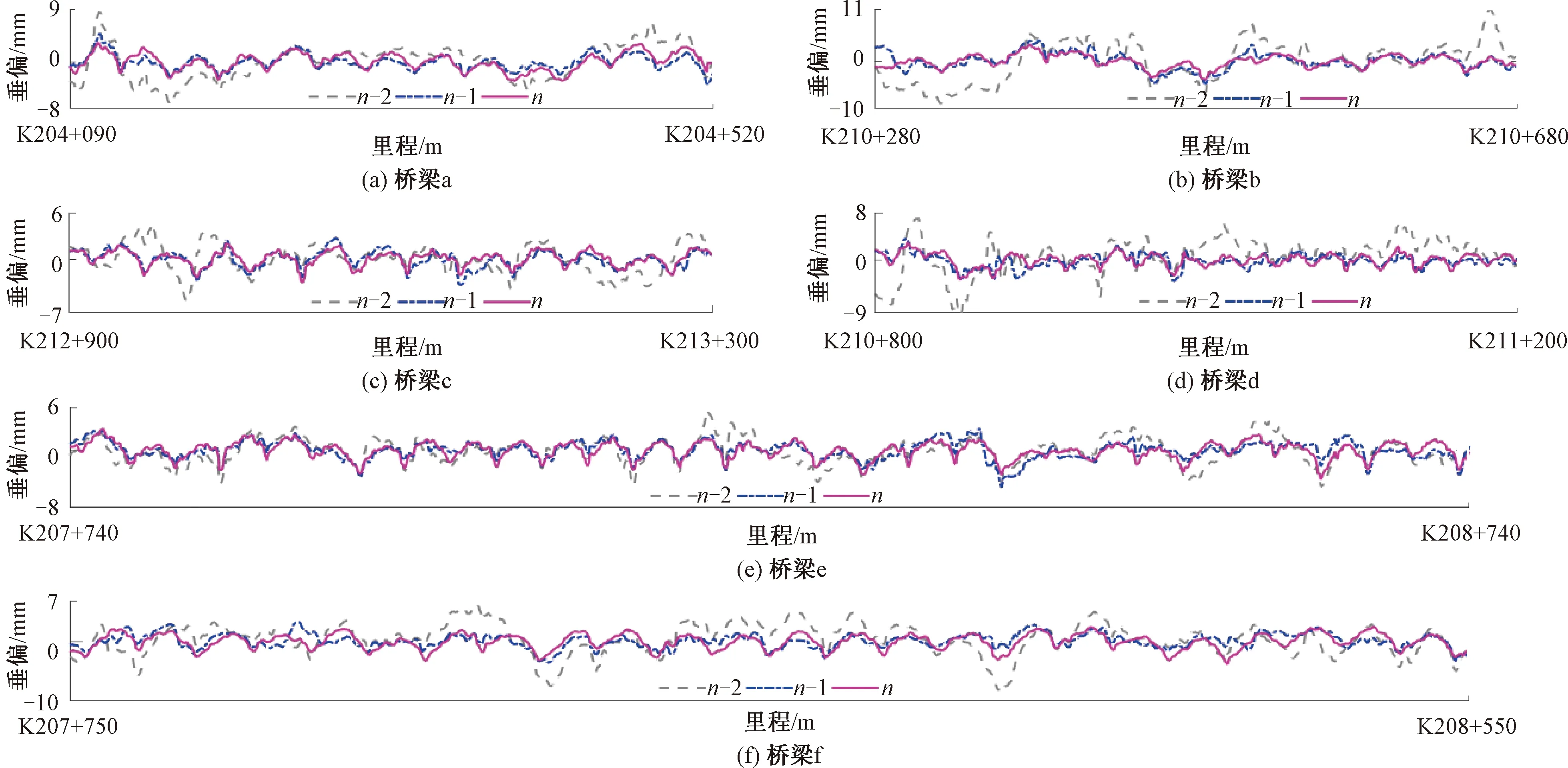
圖2 多跨32 m簡(jiǎn)支梁橋有砟軌道最后三次精搗后垂向偏差變化

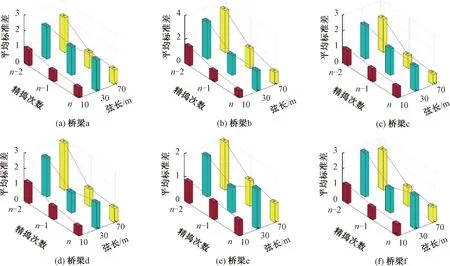
圖3 最后三次精搗后不同弦長(zhǎng)軌道高低的平均標(biāo)準(zhǔn)差變化

由圖2垂向偏差波形變化知,n-1次較n-2次精搗后波幅顯著減小,但n次(最后一次)較n-1次精搗后波幅變化微弱,且呈現(xiàn)出連續(xù)周期性上拱,波長(zhǎng)固定為32.75 m,與32 m簡(jiǎn)支梁橋的跨距保持一致。根據(jù)圖3可知,n-1次和n次精搗作業(yè),弦長(zhǎng)10、30、70 m的高低不平順改善率[15]平均為30.1%、35.2%、55.3%和16.2%、-21.7%、21.9%。表明第n-1次精搗作業(yè)后,軌道3種弦長(zhǎng)的高低均有顯著提升,尤其是長(zhǎng)弦70 m,其改善率高達(dá)55.3%。第n次精搗作業(yè)后,軌道10、70 m弦長(zhǎng)的高低改善放緩,但30 m弦長(zhǎng)對(duì)應(yīng)的平均標(biāo)準(zhǔn)差較精搗前反而增加21.7%,且顯著高于10、70 m弦長(zhǎng)。綜合來(lái)看,最后一次精搗作業(yè)起道抄平效果甚微,尤其精搗后30 m弦長(zhǎng)的軌道高低不平順不僅無(wú)改善,甚至有惡化之勢(shì)。

盡管軌道初始形位各異,但經(jīng)過(guò)重復(fù)的搗穩(wěn)聯(lián)合整道作業(yè)后,多跨32 m簡(jiǎn)支梁橋有砟軌道逐漸呈顯著的周期性上拱形態(tài),且通過(guò)增加搗固遍數(shù)亦難以將其消除。依據(jù)垂向偏差指導(dǎo)搗固車精搗作業(yè),即使梁體存在徐變,垂向偏差中亦包含了徐變引發(fā)的上拱量。精搗后垂向偏差表明軌道上拱并未消除,此后起道抄平作業(yè)幾乎再無(wú)效果可言。此外,梁體的混凝土徐變引發(fā)軌道上拱是一個(gè)緩慢、長(zhǎng)期的過(guò)程[16],而有砟軌道精測(cè)精搗為短暫的持續(xù)作業(yè)行為。因此,簡(jiǎn)支梁橋有砟軌道精測(cè)精搗后上拱之成因與混凝土徐變關(guān)系不大。由于鐵路簡(jiǎn)支梁橋整體結(jié)構(gòu)多具有連續(xù)布置、多等跨的特點(diǎn),致使精搗作業(yè)后各跨軌道呈周期性上拱。若軌道以橋梁跨距為波長(zhǎng)的周期性上拱幅值過(guò)大,將造成軌道垂向連續(xù)多(長(zhǎng))波不平順。這不僅會(huì)使以100 ～200 km/h速度開行的車輛的車體平穩(wěn)性惡化,軌道形位劣化加速及車輛-軌道部件損傷,甚至可能激勵(lì)列車產(chǎn)生車-橋共振。因此,迫切需要探究梁上有砟軌道精搗后上拱的成因和解決辦法,以便有效地控制或減弱其影響,確保列車在橋上安全平穩(wěn)地行駛。

2 搗固車起道抄平誤差模型及靜態(tài)修正

軌道垂向不平順整正包括縱向矢距(以下簡(jiǎn)稱矢距)檢測(cè)和起道抄平,起道抄平采用三點(diǎn)(R、M、F)式精搗控制[17],見(jiàn)圖4。R、F間張緊一根鋼繩作為搗固車矢距檢測(cè)的基準(zhǔn)弦(圖中紅色虛線),R位于已整修完畢(精搗后)的軌道上,F位于未整修(精搗前)的軌道上。M為起道抄平、搗固作業(yè)點(diǎn),該點(diǎn)裝有矢距傳感器。依據(jù)M處軌道矢距HM(由于矢距遠(yuǎn)遠(yuǎn)小于基準(zhǔn)弦長(zhǎng)度,矢距近似為圖中HM,并定義基準(zhǔn)弦偏下為負(fù)),mm,即可實(shí)現(xiàn)自動(dòng)起道抄平作業(yè)(近似搗固)。近似搗固依靠長(zhǎng)度為RF的基準(zhǔn)弦對(duì)軌道進(jìn)行平滑整正,本質(zhì)為低通濾波。實(shí)際上,受基準(zhǔn)弦長(zhǎng)度的限制,近似搗固難以消除超過(guò)基準(zhǔn)弦長(zhǎng)的軌道中長(zhǎng)波不平順。若預(yù)先由精測(cè)獲得基準(zhǔn)弦前端F處的軌道垂向偏差vF,則三點(diǎn)式精搗M處軌道的理論起道量lM為

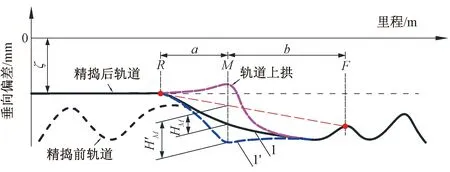
圖4 縱向起道抄平誤差

( 1 )

式中:a為RM的長(zhǎng)度;b為MF的長(zhǎng)度;ζ為預(yù)留量(預(yù)留量是指軌道設(shè)計(jì)高程面與精搗后實(shí)際高程面之間的高差),mm。

將作業(yè)段內(nèi)各點(diǎn)里程、垂向偏差和預(yù)留量作為精搗方案輸入車載ALC計(jì)算機(jī),ALC自動(dòng)計(jì)算各點(diǎn)起道量并實(shí)施起道抄平、搗固作業(yè),以此實(shí)現(xiàn)軌道垂向不平順的控制。

2.1 搗固車起道抄平誤差模型

搗固作業(yè)中除車輛荷載以外,搗固裝置還向道床傳遞巨大擠壓力。受搗固車動(dòng)荷載影響,梁體受擠壓力而處于下彎變形狀態(tài),軌道垂向狀態(tài)由1變?yōu)?′,見(jiàn)圖4。此時(shí),M處軌道實(shí)際矢距變?yōu)镠′M,則M處軌道的實(shí)際起道量為

( 2 )

結(jié)合式( 1 ),并考慮-H′M>-HM,推得搗固車在橋梁各跨精搗作業(yè)時(shí),實(shí)際起道量大于理論起道量,并與作業(yè)點(diǎn)矢距的變化直接相關(guān)。搗固車荷載與擠壓力消失后,梁體恢復(fù)至恒載狀態(tài),軌道隨梁體回彈產(chǎn)生垂向不平順,最終表現(xiàn)為自梁端至跨中逐漸向上彎拱,即軌道上拱,見(jiàn)圖4。搗固車動(dòng)荷載作用下的梁體撓度變形致使搗固車起道抄平產(chǎn)生誤差,則M處起道抄平誤差eM為

eM=l′M-lM=-H′M+HM

( 3 )

進(jìn)一步可得,在橋梁任意里程k處,搗固車起道抄平誤差模型(Lifting and Levelling Error Model,LLEM)的一般表達(dá)式為

ek=l′k-lk=-H′k+Hk

( 4 )

式中:lk、l′k分別為里程k處的理論起道量和實(shí)際起道量;Hk為里程k處軌道矢距,H′k為里程k處搗固車動(dòng)荷載作用下的軌道矢距。

綜上所述,軌道上拱是搗固作業(yè)點(diǎn)實(shí)際矢距發(fā)生變化引入起道抄平誤差所致,是作業(yè)中梁體受搗固車動(dòng)荷載作用的表現(xiàn)結(jié)果。為控制軌道上拱,需對(duì)輸入車載ALC計(jì)算機(jī)的軌道垂向偏差做修正處理,以消除搗固車起道抄平作業(yè)中的這一系統(tǒng)誤差。因此,探究軌道上拱的數(shù)學(xué)表現(xiàn)形式是解決問(wèn)題的關(guān)鍵。

2.2 垂向偏差的靜態(tài)修正函數(shù)

因軌道上拱是以橋梁跨距為波長(zhǎng)的垂向不平順,需濾除軌道垂向偏差中波長(zhǎng)較短(由擦傷、焊縫、波磨、新軌輥式矯直或檢測(cè)精度等造成的短波垂向不平順)和較長(zhǎng)(如靜態(tài)檢測(cè)累積誤差或搗固車未消除的大于跨距的長(zhǎng)波垂向不平順)的成分,即濾除垂向偏差中高頻擾動(dòng)和低頻趨勢(shì)項(xiàng)[18]。對(duì)最后一次精搗后的軌道垂向偏差作帶通濾波處理,波長(zhǎng)設(shè)置為5～35 m。 圖5為總長(zhǎng)為L(zhǎng)的多跨32 m簡(jiǎn)支梁橋有砟軌道垂向偏差帶通濾波前后示意。

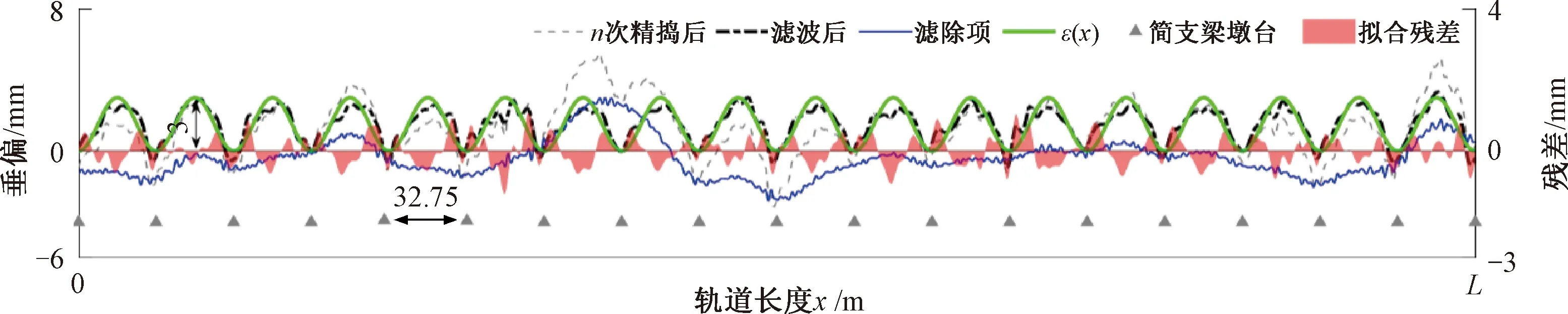
圖5 多跨32m簡(jiǎn)支梁橋有砟軌道垂向偏差帶通濾波及上拱擬合示意

濾除垂向偏差中高頻擾動(dòng)和低頻的大幅度趨勢(shì)項(xiàng)后,垂向偏差數(shù)據(jù)更加中心化,軌道上拱特性更為顯著。濾波后的垂向偏差表明精搗后軌道呈周期性上拱,上拱的波長(zhǎng)固定為32.75 m,與32 m簡(jiǎn)支梁跨距保持一致,波谷對(duì)應(yīng)簡(jiǎn)支梁墩臺(tái)處,波峰對(duì)應(yīng)于跨中。考慮濾波后垂向偏差數(shù)據(jù)規(guī)律變化的特點(diǎn),以簡(jiǎn)支梁跨距為周期的正弦函數(shù)作為目標(biāo)函數(shù),依據(jù)最小二乘作曲線擬合。擬合殘差見(jiàn)圖5,以整體擬合殘差的均方根誤差最小為準(zhǔn)則,得軌道上拱的最優(yōu)擬合函數(shù)為

x∈[0,32.75]

( 5 )

式中:x為自32 m簡(jiǎn)支梁前端起始墩臺(tái)中心沿軌道的長(zhǎng)度,m。

由ε(x)知,軌道上拱最大幅度約為3 mm,位于跨中,見(jiàn)圖5。梁上軌道上拱是搗固車起道抄平誤差的表現(xiàn)形式。那么ε(x)則為描述起道抄平誤差ek的數(shù)學(xué)模型,又稱為垂向偏差的靜態(tài)修正函數(shù)。若橋梁里程k處軌道垂向偏差為vk,則靜態(tài)修正后的軌道垂向偏差vSCk為

vSCk=vk+ε(x)=vk+ε(k-k0)

( 6 )

式中:k0為距離里程k處最近的小里程端墩臺(tái)中心里程。

將k、vSCk和ζ輸入至車載ALC計(jì)算機(jī),ALC依據(jù)式( 2 )即可計(jì)算各跨軌道經(jīng)過(guò)靜態(tài)修正后的起道量。式( 6 )為顧及搗固車起道抄平作業(yè)中的系統(tǒng)誤差,通過(guò)靜態(tài)修正函數(shù)ε(x)的補(bǔ)償,實(shí)現(xiàn)減弱或消除梁體上軌道上拱。

3 軌道預(yù)拱模型及動(dòng)態(tài)修正

靜態(tài)檢測(cè)為軌道荷載忽略不計(jì)的軌道幾何形位測(cè)量,動(dòng)態(tài)檢測(cè)則為擬真測(cè)試。動(dòng)態(tài)檢測(cè)時(shí)軌道幾何形位更加接近列車運(yùn)行時(shí)的真實(shí)狀態(tài),但精搗方案是依據(jù)靜態(tài)檢測(cè)數(shù)據(jù)計(jì)算確定的。為提高列車在32 m簡(jiǎn)支梁橋有砟軌道的動(dòng)態(tài)平順性,精搗作業(yè)時(shí)應(yīng)顧及簡(jiǎn)支梁橋軌道動(dòng)靜態(tài)垂向不平順的差異。動(dòng)態(tài)檢測(cè)得到的是慣性基準(zhǔn)下一定截止波長(zhǎng)的軌道不平順數(shù)據(jù),靜態(tài)檢測(cè)獲得的是幾何基準(zhǔn)下軌道的橫垂向偏差。動(dòng)態(tài)檢測(cè)里程誤差遠(yuǎn)大于靜態(tài)檢測(cè)的,兩者數(shù)據(jù)無(wú)法直接比較,需作數(shù)據(jù)預(yù)處理[18],主要包括動(dòng)態(tài)檢測(cè)里程誤差修正(統(tǒng)一里程)和動(dòng)靜態(tài)檢測(cè)截止波長(zhǎng)35 m的高通濾波處理(統(tǒng)一波長(zhǎng))。動(dòng)靜態(tài)檢測(cè)軌道垂向波形在里程上并不吻合,但相鄰墩臺(tái)間均有上拱特性。利用這一特性,對(duì)動(dòng)態(tài)檢測(cè)里程作局部修正處理,便可解決動(dòng)靜態(tài)檢測(cè)波形錯(cuò)位的問(wèn)題。里程誤差修正主要有最小二乘法、相關(guān)系數(shù)法[19]。鑒于靜態(tài)檢測(cè)里程誤差極小,把靜態(tài)檢測(cè)垂向偏差所確定的墩臺(tái)位置作為校正點(diǎn),采用基于局部波形匹配的方法修正動(dòng)態(tài)檢測(cè)里程誤差,見(jiàn)圖6。

圖6 里程修正前后的動(dòng)靜態(tài)檢測(cè)軌道垂向波形示意

經(jīng)動(dòng)態(tài)檢測(cè)里程誤差修正和動(dòng)靜態(tài)檢測(cè)高通濾波處理,動(dòng)靜態(tài)檢測(cè)軌道垂向波形在里程與波長(zhǎng)上實(shí)現(xiàn)統(tǒng)一。圖7為總長(zhǎng)為L(zhǎng)的多跨32 m簡(jiǎn)支梁橋,預(yù)處理后的動(dòng)靜態(tài)檢測(cè)軌道垂向波形及互差示意。

圖7 多跨32 m簡(jiǎn)支梁橋有砟軌道動(dòng)靜態(tài)檢測(cè)垂向波形及互差示意

由圖7所示波形可知,多跨32 m簡(jiǎn)支梁橋有砟軌道動(dòng)靜態(tài)檢測(cè)垂向不平順互差同樣呈現(xiàn)以跨距為波長(zhǎng)的周期性變化,且自各梁端支點(diǎn)處至跨中逐漸增大,但在隧道洞口的無(wú)砟軌道與有砟軌道過(guò)渡段、有砟軌道路基段、有砟軌道或無(wú)砟軌道隧道段均未有類似的規(guī)律性存在。鑒于動(dòng)態(tài)檢測(cè)時(shí),軌道垂向狀態(tài)更加接近列車運(yùn)行時(shí)的狀態(tài),精搗作業(yè)中,若依據(jù)動(dòng)靜態(tài)檢測(cè)各跨垂向不平順的互差規(guī)律,為簡(jiǎn)支梁橋有砟軌道預(yù)設(shè)合理的上拱量,將有利于改善高速列車通過(guò)時(shí)垂向的動(dòng)態(tài)平順性。

控制梁體上有砟軌道的預(yù)拱,預(yù)拱量的確定是關(guān)鍵。同樣考慮互差數(shù)據(jù)呈周期性變化的特點(diǎn),以跨距為周期的正弦函數(shù)作為目標(biāo)函數(shù),采用最小二乘曲線擬合,擬合殘差見(jiàn)圖7。以整體擬合殘差的均方根誤差最小為準(zhǔn)則,得32 m簡(jiǎn)支梁橋有砟軌道預(yù)拱模型(Ballasted Track Pre-camber Setting Model,BTPCM)為

x∈[0,32.75]

( 7 )

由η(x)可知,32 m簡(jiǎn)支梁橋有砟軌道動(dòng)靜態(tài)檢測(cè)垂向互差最大約為1 mm,同樣位于跨中,見(jiàn)圖7。依據(jù)BTPCM,對(duì)式( 6 )所得的靜態(tài)檢測(cè)垂向偏差進(jìn)行修正,即

vDCk=vSCk-η(x)=vk+ε(k-k0)-η(k-k0)

( 8 )

式中:η(k-k0)為依據(jù)BTPCM確定的32 m簡(jiǎn)支梁橋有砟軌道精搗預(yù)拱量。

式( 8 )所得垂向偏差vDCk是在補(bǔ)償搗固車縱向抄平誤差,同時(shí)依據(jù)BTPCM為梁上有砟軌道設(shè)置預(yù)拱量,以提高32 m簡(jiǎn)支梁橋有砟軌道垂向的動(dòng)態(tài)平順性。設(shè)置預(yù)拱的軌道,其10 m弦最大矢距約±0.2 mm,30 m弦最大矢距約±0.98 mm。據(jù)此,建議有砟軌道靜態(tài)驗(yàn)收時(shí),10 m和30 m弦高低容許偏差應(yīng)顧及橋梁段預(yù)設(shè)上拱量的這一特性。

4 模型驗(yàn)證與探討

為檢驗(yàn)起道抄平誤差模型和有砟軌道預(yù)拱模型的有效性,在某新建鐵路線路有砟軌道上由GPS/INS組合導(dǎo)航軌道快速檢測(cè)系統(tǒng)配合DWL-48K型搗固車做精測(cè)精搗工程試踐驗(yàn)證。工程試驗(yàn)段有多跨32 m簡(jiǎn)支梁橋16座,橋梁占比約為24%。圖8為某長(zhǎng)為1.2 km(K143+300—K144+500)的多跨32 m簡(jiǎn)支梁橋段,工程試驗(yàn)后的動(dòng)靜態(tài)檢測(cè)軌道垂向不平順和車體垂向加速度波形示意。圖8所示為墩臺(tái)號(hào)1～13范圍內(nèi)靜態(tài)修正區(qū)段,起道量計(jì)算僅采用靜態(tài)修正函數(shù)來(lái)補(bǔ)償起道抄平誤差;墩臺(tái)號(hào)13～25范圍內(nèi)為動(dòng)靜態(tài)修正區(qū)段,起道量顧及LLEM和BTPCM聯(lián)合計(jì)算,補(bǔ)償起道抄平誤差的同時(shí)設(shè)置軌道預(yù)拱量;墩臺(tái)號(hào)25～37范圍內(nèi)為未修正區(qū)段,起道量由靜態(tài)檢測(cè)垂向偏差直接確定,即不作起道抄平誤差和軌道預(yù)拱量修正。圖8數(shù)據(jù)來(lái)源:n次精搗前、后的垂向偏差由靜態(tài)檢測(cè)精測(cè)確定,高低為動(dòng)態(tài)檢測(cè)長(zhǎng)波通道輸出值,車體垂向加速度為動(dòng)態(tài)檢測(cè)車20 Hz的低通濾波輸出值。

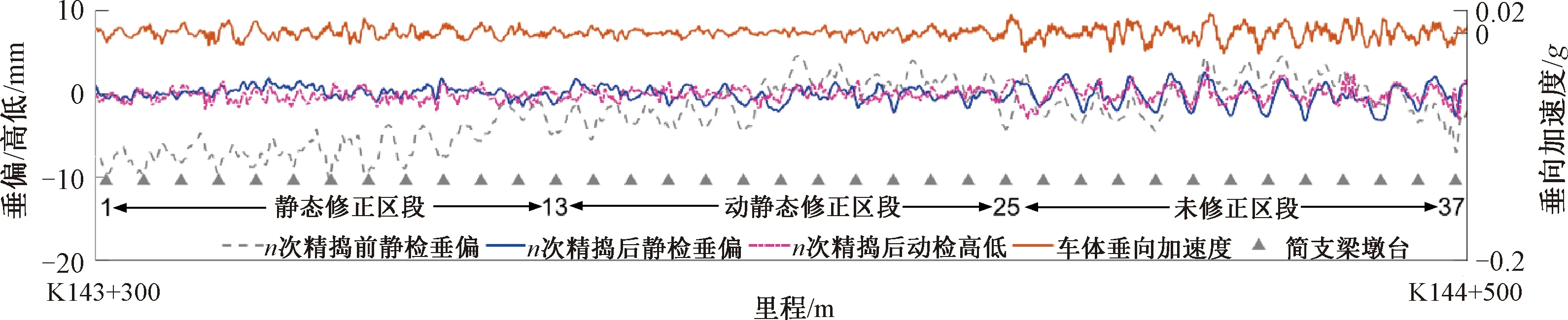
圖8 多跨32m簡(jiǎn)支梁橋軌道垂向不平順及車體垂向加速度波形示意

從靜態(tài)檢測(cè)垂向偏差波形來(lái)看,搗固車n次精搗作業(yè)后,軌道垂向平順性,靜態(tài)修正區(qū)段優(yōu)于動(dòng)靜態(tài)修正區(qū)段;從動(dòng)態(tài)檢測(cè)高低波形來(lái)看,軌道垂向平順性,動(dòng)靜態(tài)修正區(qū)段卻優(yōu)于靜態(tài)修正區(qū)段;但不論是靜態(tài)檢測(cè)垂向偏差亦或動(dòng)態(tài)檢測(cè)高低波形,未修正區(qū)段各跨有砟軌道精搗后仍舊呈顯著的周期性上拱。至于車體垂向加速度波形,動(dòng)靜態(tài)修正區(qū)段加速度的波動(dòng)最為平緩,靜態(tài)修正區(qū)段次之,而在未修正區(qū)段簡(jiǎn)支梁墩臺(tái)處和跨中,出現(xiàn)大量的垂向加速度峰值。

為具體對(duì)比和顯示動(dòng)靜態(tài)修正對(duì)軌道垂向平順性控制的效果,從最后一次精搗前后靜態(tài)檢測(cè)垂向偏差三種弦長(zhǎng)對(duì)應(yīng)的平均標(biāo)準(zhǔn)差、動(dòng)態(tài)檢測(cè)高低不平順PSD、車體垂向加速度分布三個(gè)方面進(jìn)行對(duì)比分析,見(jiàn)圖9。

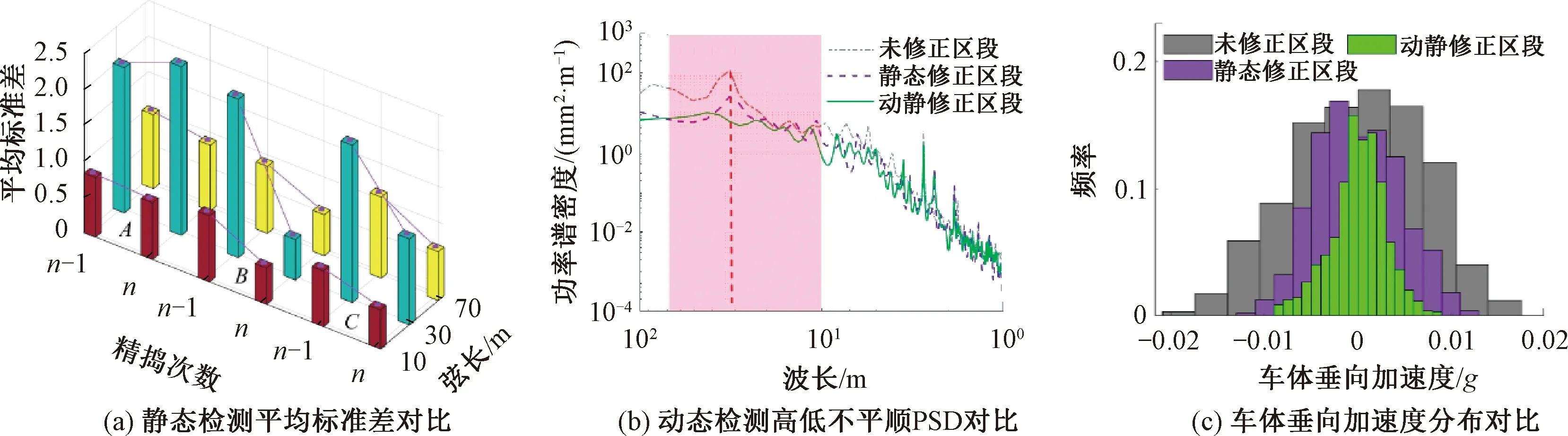
圖9 軌道垂向平順性控制對(duì)比

圖9(a)中,A為未修正區(qū)段,B為靜態(tài)修正區(qū)段,C為動(dòng)靜態(tài)修正區(qū)段。第n次精搗作業(yè)后,三個(gè)區(qū)段各弦長(zhǎng)(10、30、70 m)的軌道高低不平順改善率分別為4.8%、-16%、10.9%,45.1%、74.4%、38.7%和29.7%、45.4%、39.8%,表明B、C區(qū)段三種弦長(zhǎng)下軌道高低不平順得到極大改善,尤其30 m弦長(zhǎng)改善74.4%和45.4%最為顯著,這是因?yàn)橛许能壍郎瞎暗玫接行p弱或消除。n次精搗后,10 m弦和70 m弦對(duì)應(yīng)的平均標(biāo)準(zhǔn)差,C區(qū)段略高于B區(qū)段;30 m弦對(duì)應(yīng)的平均標(biāo)準(zhǔn)差,C區(qū)段明顯高于B區(qū)段,表明簡(jiǎn)支梁橋精搗中僅補(bǔ)償起道抄平誤差,能有效地減弱或消除有砟軌道上拱,獲得更優(yōu)的靜態(tài)垂向平順性。

由圖9(b)中動(dòng)態(tài)檢測(cè)不平順PSD曲線,未修正區(qū)段包含大量以32 m簡(jiǎn)支梁橋的跨距為波長(zhǎng)的周期性不平順。靜態(tài)修正區(qū)段,盡管圖9(a)表明已消除了各跨軌道上拱,但動(dòng)態(tài)檢測(cè)高低顯示,仍舊會(huì)出現(xiàn)一定幅度的以簡(jiǎn)支梁橋跨距為波長(zhǎng)的周期性不平順。動(dòng)靜態(tài)聯(lián)合修正區(qū)段,幾乎完全消除了這種周期性不平順,表明簡(jiǎn)支梁橋有砟軌道精搗中補(bǔ)償起道抄平誤差的同時(shí),設(shè)置預(yù)拱量可獲得更優(yōu)的動(dòng)態(tài)垂向平順性。

根據(jù)圖9(c)統(tǒng)計(jì)結(jié)果,未修正區(qū)段、靜態(tài)修正區(qū)段和動(dòng)靜態(tài)修正區(qū)段車體垂向加速度均值約為0,標(biāo)準(zhǔn)差約為0.007g、0.004 5g和0.003g。表明采用動(dòng)靜態(tài)聯(lián)合修正,軌道精搗后的車體垂向動(dòng)力響應(yīng)最小,舒適性最優(yōu),具有更高的動(dòng)態(tài)垂向平順性。

新建鐵路有砟軌道線路精測(cè)精搗工程實(shí)踐驗(yàn)證了LLEM和BTPCM在減弱或消除32 m簡(jiǎn)支梁橋有砟軌道精搗后上拱的有效性。換而言之,就有砟軌道平順性而言,精測(cè)精搗中補(bǔ)償起道抄平誤差的同時(shí)設(shè)置預(yù)拱量,能夠切實(shí)有效地提高梁體上有砟軌道的動(dòng)態(tài)垂向平順性。

5 結(jié)論

大量的橋梁有砟軌道精測(cè)精搗實(shí)踐顯示,垂向不平順表現(xiàn)出不同于其他線下工程的上拱特性。研究橋梁有砟軌道精測(cè)精搗后上拱的成因,及32 m簡(jiǎn)支梁動(dòng)靜態(tài)修正模型LLEM和BTPCM,經(jīng)工程實(shí)踐驗(yàn)證正確有效,得出以下主要結(jié)論:

(1)有砟軌道橋梁段存在精搗作業(yè)難以消除的軌道上拱,造成多跨橋梁軌道垂向多(長(zhǎng))波不平順。軌道上拱是因搗固作業(yè)點(diǎn)矢距發(fā)生變化引入起道抄平誤差所致,是作業(yè)中梁體受搗固車動(dòng)荷載影響的結(jié)果。32 m簡(jiǎn)支梁橋有砟軌道精搗后靜態(tài)垂向不平順?lè)翟诳缰羞_(dá)3 mm,波長(zhǎng)固定為32.75 m。

(2)橋梁有砟軌道精搗后,梁上靜態(tài)檢測(cè)與動(dòng)態(tài)檢測(cè)的軌道垂向不平順?lè)挡幌嗟?其垂向不平順互差自梁端至跨中逐漸增大。32 m簡(jiǎn)支梁橋有砟軌道在跨中的動(dòng)靜態(tài)垂向不平順互差可達(dá)1 mm,波長(zhǎng)固定為32.75 m。

(3)32 m簡(jiǎn)支梁橋有砟軌道精測(cè)精搗中,采用起道抄平誤差模型(LLEM)能消除或減弱軌道上拱,進(jìn)而有效地控制梁上軌道靜態(tài)垂向長(zhǎng)波不平順;精測(cè)精搗中補(bǔ)償起道抄平誤差并顧及有砟軌道預(yù)拱模型(BTPCM),更能有效提高32 m簡(jiǎn)支梁橋有砟軌道動(dòng)態(tài)垂向平順性。

(4)有砟軌道靜態(tài)驗(yàn)收時(shí),經(jīng)LLEM和BTPCM聯(lián)合修正后的32 m簡(jiǎn)支梁橋段,應(yīng)與其他線下工程區(qū)分開來(lái),垂向不平順容許偏差的管理值應(yīng)顧及梁上有砟軌道預(yù)拱量。

高速鐵路有砟軌道的大量建設(shè),以及新建鐵路橋梁占比和多等跨簡(jiǎn)支梁橋的不斷增加,使得科學(xué)有效地控制橋上有砟軌道的動(dòng)態(tài)不平順,兼具科學(xué)理論意義和工程實(shí)用價(jià)值。本文研究結(jié)論不僅適用于32 m跨簡(jiǎn)支梁橋有砟軌道精測(cè)精搗,對(duì)其他類型或跨距橋梁的有砟軌道精測(cè)精搗及其相關(guān)技術(shù)標(biāo)準(zhǔn)的制定也有參考價(jià)值。