高頻循環荷載作用下砂土抗剪強度試驗研究

陜 耀，陳 平，3，周順華，葉偉濤，代 寧

(1.同濟大學 道路與交通工程教育部重點實驗室，上海 201804；2.上海市軌道交通結構耐久與系統安全重點實驗室，上海 201804；3.中鐵城市發展投資集團有限公司，四川 成都 610218)

顆粒土常受車輛交通振動、地震、爆破、施工作業、機械振動等的影響。例如,高速列車的振動會導致路基局部沉降甚至破壞,嚴重影響高速列車運行的平穩性和行車安全性[1-3]。當車速從350 km/h提高至400 km/h,甚至再往上突破時,由高頻振動所引發的路基土體動力學問題將會愈加突出。列車振動引起的彈性波在土體內擴散和傳播,會導致土體顆粒間的摩阻力下降,從而導致土體產生顯著變形并影響上部以及鄰近結構[4-10]。目前,車致高頻循環荷載作用所引起的軌下基礎散體材料的物理力學機制,尤其是土體的強度變化尚不明確。因此,通過高頻循環振動下的散體材料力學行為的研究,可以對高鐵路基的局部破壞和沉降中顆粒土的受力和變形特性產生新的認識。振動中顆粒土的強度不僅取決于振動特性,如加速度、頻率和振幅,還與顆粒土的物理性質,如含水量、粒度分布、顆粒形狀、相對密度或孔隙比、顆粒土的黏聚力和內摩擦角等因素有關。除此之外,散體材料的振動特性在地震、振動流化床以及其它物理力學領域也存在相應的問題[11-22],國內外學者采用室內模型試驗、動直剪試驗和動三軸試驗等手段,研究了振動作用對顆粒材料尤其是砂土強度特性的影響。

Barkan[11]通過改進的動直剪儀研究了水平振動對砂土抗剪強度參數的影響,研究表明,振動強度是決定砂土內摩擦角和孔隙率大小的主要參數,并且砂土的內摩擦角和孔隙率都隨振動強度的增大而不斷減小。Grossman[12]認為振動會引起顆粒材料的流動,并將其歸因于顆粒和界面之間的非彈性摩擦作用。Aumaitre等[13]研究了顆粒材料在正弦振動下的力學行為,結果表明加速度對顆粒運動狀態影響較大。Raihane等[22]的試驗結果證實了文獻[13]的研究結論。Johnson等[14-15]對玻璃微珠開展了振動直剪試驗,發現高頻振動會引起顆粒材料結構的破壞,導致剪切應力下降。Denies等[16-17]發現振動會導致砂土抗剪強度顯著降低,并將砂土的運動分為3類:當垂直振動的加速度幅值小于1g時,砂土表現為振動壓縮;當加速度幅值接近1g時,砂土自由表面的顆粒產生流動;當加速度幅值大于1g時,砂土會發生對流和分層。

最近,文獻[18-19]通過改進的動直剪試驗發現結構面的粗糙度對砂土試樣強度有顯著影響。此外,Taslagyan等[20-21]通過改進動直剪儀研究了一系列不同正應力下振動強度對干砂抗剪強度的影響,統計了砂土在剪切作用下的峰值、殘余和振動殘余強度,結果表明:振動強度的增大有效降低了顆粒材料在峰值和殘余狀態下的內摩擦角。但由于直剪試驗難以真實地反映三軸應力狀態下振動對砂土抗剪強度的影響,且砂土在殘余剪切強度下,各影響因素(如振動強度、有效圍壓、初始相對密實度、含水率和振動頻率等)對砂土殘余抗剪強度指標的影響,未發現有相關文獻展開研究。因此,本文采用自主研制的靜載與高頻循環荷載耦合作用三軸儀[23-24],以國內常見的福建平潭標準砂為研究對象,對砂土在振動條件下的殘余抗剪強度損失展開研究,分析振動強度、有效圍壓、初始相對密實度以及含水率和振動頻率等因素對砂土殘余抗剪強度損失的影響,探索砂土在高頻循環荷載作用下的力學特性。

1 試驗裝置

試驗采用可以施加高頻循環荷載的三軸儀,系統構成主要包括:加載系統、控制系統、測量和數據采集系統,以及圍壓控制系統。試驗裝置見圖1。

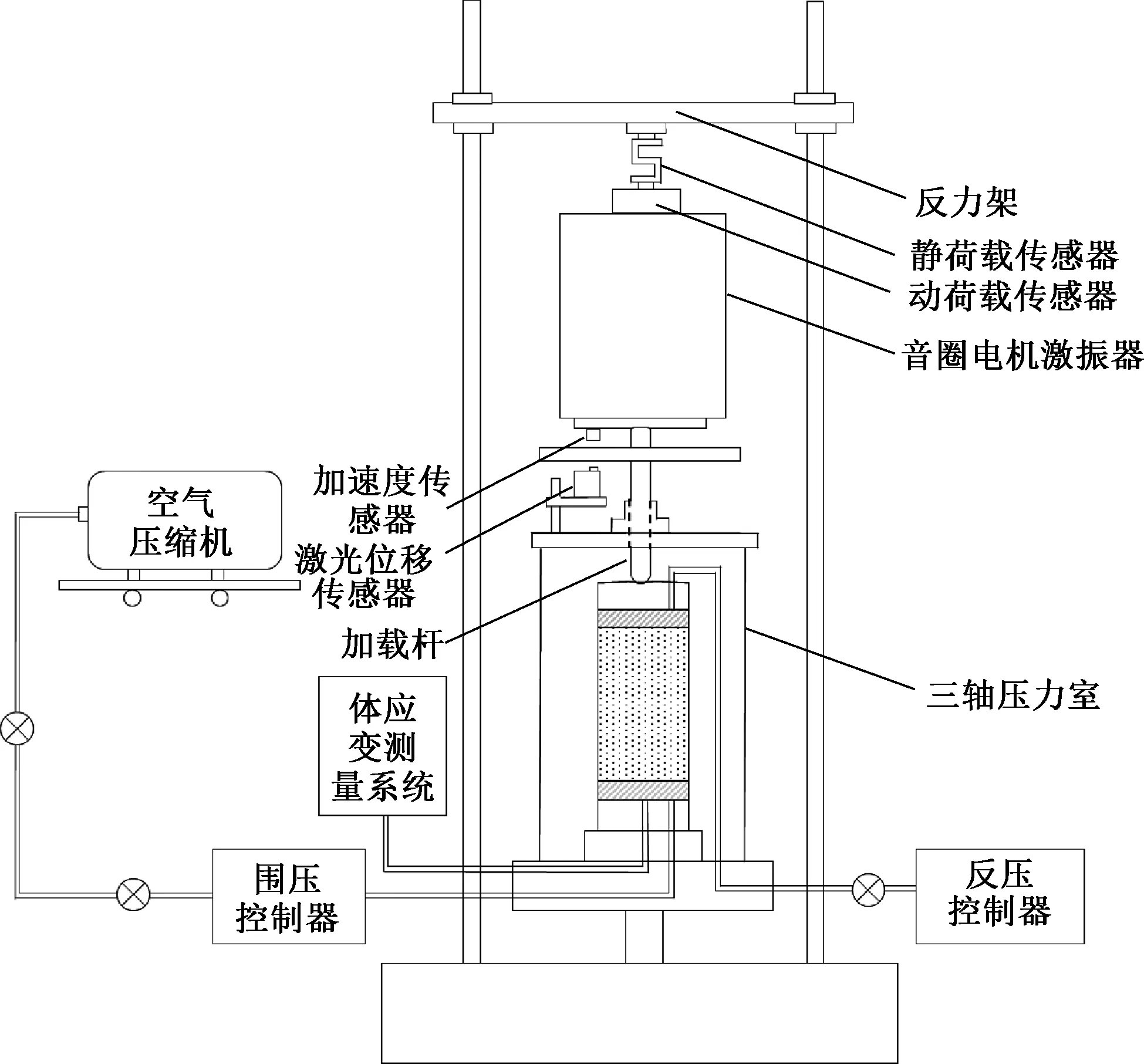
圖1 試驗裝置

靜力加載系統類似常規靜力三軸儀的結構,以恒定的軸向應變速率加載。靜力加載系統包括下部加載控制臺、試樣底座、反力架、圍壓控制系統,動力加載系統主要包括音圈電機、傳力桿。音圈電機安裝在荷載傳感器和試樣之間,振子受電流驅動,產生安培力,其振動方向為試樣同軸方向。控制系統采用音圈電機驅動器,包括直流電源、精密信號發生器和功率放大器。測量和數據采集系統包括靜荷載傳感器、動荷載傳感器、激光位移傳感器、加速度傳感器、動力測試分析系統。動荷載傳感器用來測量振動過程中動應力幅值,加速度傳感器用來測量試驗振動過程中加速度幅值。動荷載傳感器與加速度傳感器的采集頻率均為500 Hz。激光位移傳感器采集頻率可達2 000 Hz,記錄振動過程中試樣的位移幅值以及由振動引起試樣的壓縮變形情況。所有傳感器都連接到一個動力測試分析系統,來分析加速度、軸向位移以及動應力的響應情況。試驗系統相關介紹和可靠性見文獻[23-24]。

2 試驗材料與方法

2.1 試樣材料

本文試驗對象為通用的福建平潭標準砂,其顆粒級配曲線見圖2。由圖2可知,試驗所用平潭標準砂為中砂。平潭砂的基本物理指標和顆粒形狀分別見表1、圖3。

表1 平潭標準砂基本物理指標

圖2 顆粒級配曲線[23]

圖3 平潭砂顆粒形狀[23]

2.2 試樣制備

三軸試樣為圓柱形,尺寸為50 mm×100 mm(D×H),干砂試樣采用干法制備[25]。制樣時,試樣通過分層壓實至所需密度,當每層加至預定高度,通過小錘輕輕敲擊對開模外壁使試樣表面平整。制樣結束后,通過給試樣內部施加負壓保證試樣保持原狀。飽和砂土試樣采用濕法制備。制樣前,用無氣水覆蓋砂土并煮沸,使砂土內空氣完全排盡。待其冷卻后,按文獻[23]制備飽和砂土試樣。當加砂完成時,通過輕輕敲擊對開模使砂土試樣達到指定高度,以控制飽和試樣初始相對密實度。值得注意的是,加砂過程需保證砂土始終位于液面以下,從而減少空氣進入,提高飽和度。當試樣裝載至三軸儀后,采用反壓飽和法使試樣完全飽和。通過反壓控制方式施加加壓,為了保證試樣充分飽和,反壓從0 kPa逐級加載至100 kPa,以溶解水中的滯留空氣,直到Skempton B值不小于0.96,即試樣達到完全飽和。在試樣飽和的過程中,試樣的有效應力不得低于10 kPa,以防止試樣發生變形甚至塌陷。試樣在100 kPa的有效固結圍壓下直至沒有額外的體積變形即完成固結。飽和砂試樣制備方法見圖4。

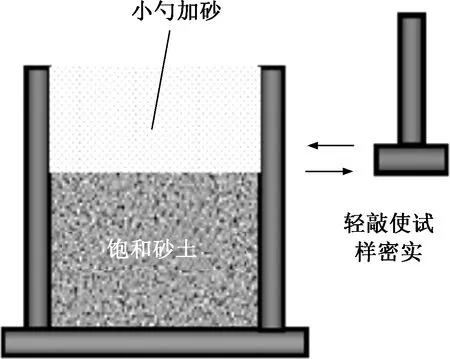
圖4 飽和砂試樣制備方法[23]

2.3 試驗方法

試驗采用應變控制模式,試樣首先以恒定剪切速率v=0.1 mm/min進行單調剪切,直至試樣接近臨界狀態。再通過音圈電機對試樣施加一定時間的動荷載,加載頻率和能量通過計算機端控制。試驗過程中,砂土的加速度、應力和應變分別通過加速度傳感器、動荷載傳感器和位移傳感器采集。試驗加載示意見圖5。

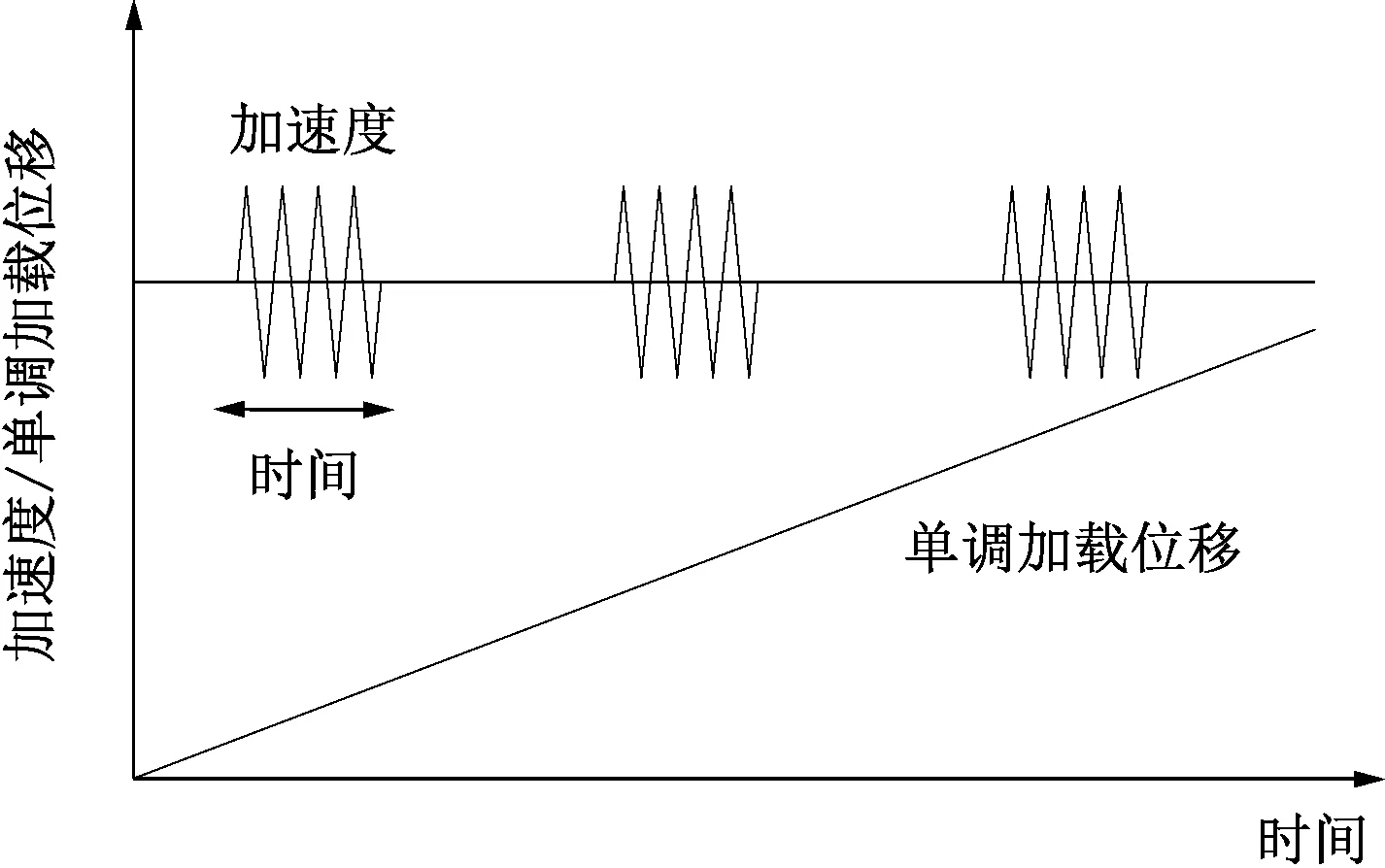
圖5 試驗加載示意

由圖5可知,隨著單調加載的進行,偏應力逐漸恢復至振動前的應力水平,再重復前述加載步驟。然而,試樣軸向應變越大,試樣內部各向異性越明顯,此時試樣與進入臨界狀態初期時的性質差異顯著,從而試驗結果差異較大。為避免因試樣充分剪切使得軸向應變過大而影響試驗結果,本文試驗的最終軸向應變不超過15%。

Zhai等[26]通過現場實測發現京滬高鐵路基土體的高頻成分主要集中于20～60 Hz。為反映振動高頻成分的影響,在研究加速度與抗剪強度損失的關系時,選取60 Hz作為試驗的加載頻率。Dai等[23]的試驗結果表明,振動時間(10～30 s)對偏應力降低的影響不大,故本試驗選擇的振動時長為10 s。由于土體性質受眾多因素的影響,本文還考慮不同初始相對密實度、有效圍壓、含水率、振動頻率等因素對砂土在高頻循環荷載作用下的力學特性的影響,試驗方案見表2。

表2 試驗方案

3 試驗結果分析

根據無黏性土庫倫公式τ=σtanφ,其中,τ為靜力剪切的剪切力;σ為正應力;內摩擦角φ為強度指標,強度損失體現為內摩擦角減小。故本文確定研究對象為內摩擦角減小值,以反映強度損失狀況。

采用有效應力法計算振動前砂土的內摩擦角,通過有效圍壓σ′分別為30、50、70 kPa條件下的靜三軸試驗,得到平潭標準砂的應力-應變關系。當試樣剪切至殘余應力狀態時,基于偏應力與有效圍壓可計算得到軸向應力,最終得到莫爾應力圓和殘余抗剪強度包絡線,干砂與飽和砂的殘余抗剪強度包絡線見圖6。由圖6可知,當Dr=0.4時,干砂的殘余內摩擦角φ1=36.66°;當Dr=0.7時,干砂的殘余內摩擦角φ2= 36.44°;當Dr=0.4時,飽和砂土的殘余內摩擦角φ3= 37.88°;當Dr=0.7時,飽和砂土的殘余內摩擦角φ4= 38.39°。

圖6 三軸試驗不同Dr殘余抗剪強度包絡線

干砂在Dr=0.7、σ′3= 50 kPa時的偏應力、豎向加速度與加載時間的關系曲線見圖7。當試樣經歷單調剪切至殘余應力狀態時,對試樣施加正弦荷載。振動強度通常用無量綱加速度a/g表示,其中,a為振動加速度;g為重力加速度。

由圖7可知,當Dr=0.7、σ′3= 50 kPa的干砂試樣單調剪切至殘余應力狀態時,對試樣施加60 Hz循環荷載,試樣很快發生強度損失。而隨著振動持續,干砂試樣強度基本保持不變。當振動停止后,隨著單調剪切繼續發展,試樣強度逐漸恢復至振前水平。即施加的高頻循環荷載對干砂試樣振動前后的抗剪強度沒有長期影響,甚至還可能產生輕微的應力硬化(振后的強度比振前的強度更高)。然而,振動確實降低了試樣的抗剪強度,因此,把振動達到穩定狀態時試樣的殘余抗剪強度稱為振動殘余抗剪強度,對應的砂土內摩

擦角稱為振動殘余內摩擦角[18,21]。振動過程中產生的剪切力τ的表達式為

τ=σtanφdi

( 1 )

Δφi=φi-φdi

( 2 )

式中:φi為振動前的砂土內摩擦角值,i=1,2,3,4;φdi為振動穩定時的砂土內摩擦角值;Δφi為振動前與振動穩定時砂土內摩擦角的差值,即砂土單調剪切內摩擦角與振動殘余內摩擦角的差值。為便于單位統一,將內摩擦角的減小進行歸一化處理,從而定義新的變量Δφi/φi為內摩擦角降比,以更好地反映砂土內摩擦角衰減比例,也間接反映殘余抗剪強度損失比例。由于飽和砂土試驗現象與干砂土相似,在此不再另行展示。

3.1 振動加速度對砂土殘余內摩擦角降比的影響

在60 Hz循環荷載作用下,干砂和飽和砂殘余內摩擦角降比與無量綱加速度a/g的關系見圖8。當單調剪切至殘余應力狀態時,砂土抗剪強度不會因加載的持續而發生較大的變化。

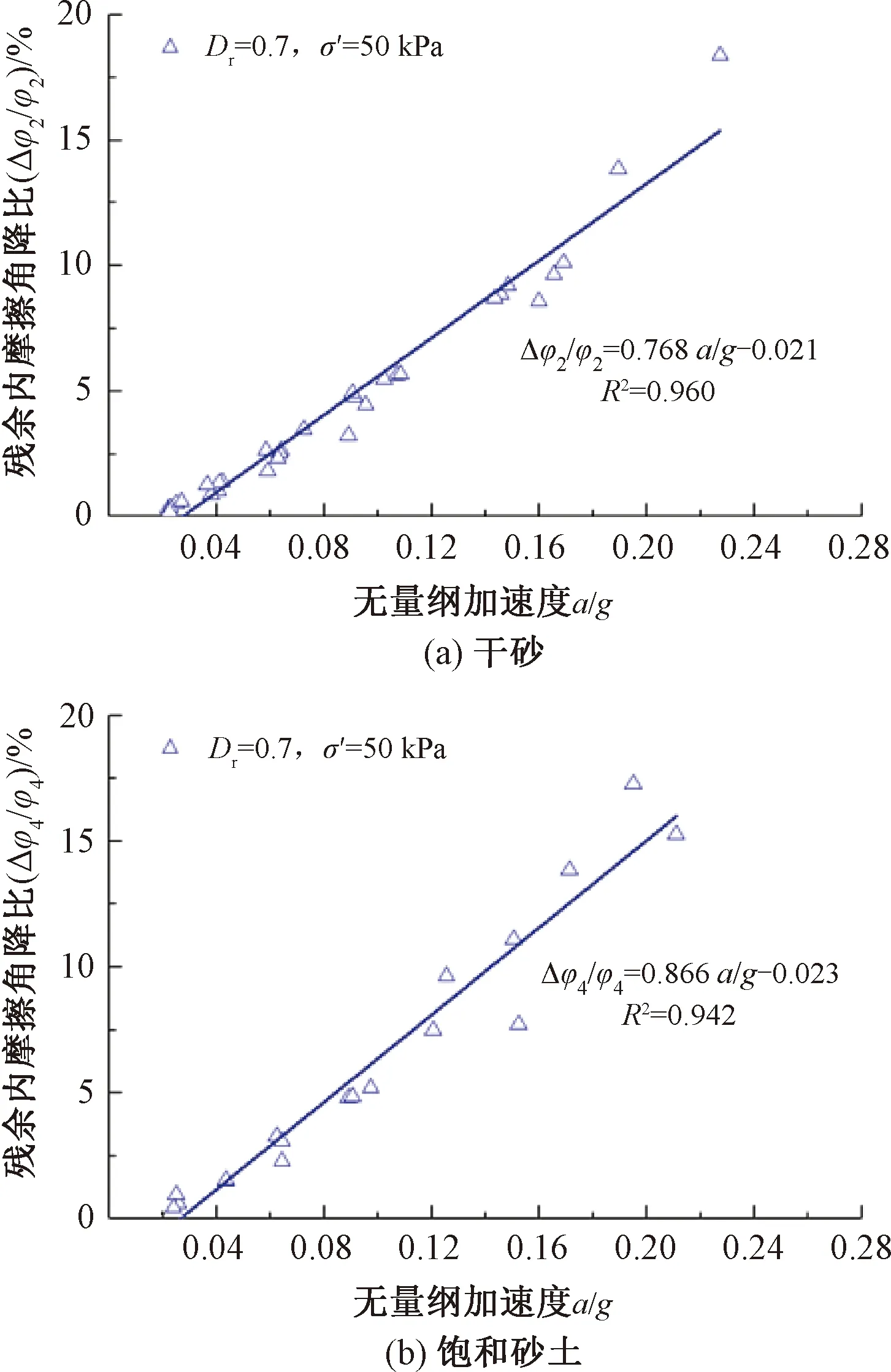
圖8 砂土殘余應力狀態下干砂、飽和砂土內摩擦角降比與加速度的關系

由圖8可知,當加速度a≤0.02g時,砂土殘余內摩擦角降比很小,幾乎可以忽略不計;當加速度a>0.02g時,砂土殘余內摩擦角逐漸衰減,砂土殘余內摩擦角降比與加速度幅值成正比。這是由于砂土的殘余抗剪強度依然能夠抵抗較小的附加振動。此時,砂土顆粒排列較為緊密,較小振動能量下砂土顆粒間的摩擦難以被克服,故當加速度較小時,砂土殘余內摩擦角衰減較小。而隨著振動加速度的不斷增大,砂土顆粒間的相互作用被逐漸克服,砂土殘余抗剪強度逐漸減小,殘余內摩擦角降比逐漸增大。

在60 Hz循環荷載作用下,殘余應力狀態下加速度幅值與砂土殘余內摩擦角降比的關系見圖9。由圖9可知,當加速度a≤0.02g時,干砂與飽和砂的殘余內摩擦角降比均較小,幾乎為零,即砂土的含水率對結果影響不大;當a>0.02g時,對于給定的加速度,干砂與飽和砂的殘余內摩擦角降比差異也較小。隨著振動加速度的增加,砂土的殘余內摩擦角降比幾乎不受含水率的影響。此外,飽和試樣在基于固結排水條件下進行的,即超孔隙水壓力不會累積且在較短的時間內很快消散,從而導致超孔隙水壓力對飽和砂土殘余抗剪強度的影響不顯著,干砂和飽和砂的試驗結果差異不大。因此,在靜載與高頻循環荷載耦合作用下,本試驗振動加速度范圍內飽和砂與干砂的殘余抗剪強度變化差異不大。

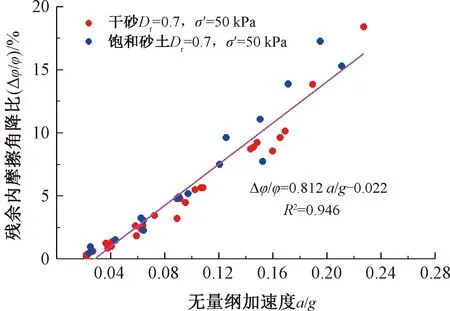
圖9 殘余應力狀態下干砂土與飽和砂土對比

3.2 初始相對密實度對砂土殘余內摩擦角的影響

在60 Hz循環荷載作用下,干砂土初始相對密實度對殘余內摩擦角降比的影響見圖10。圖10中,Dr分別為0.4、0.7,有效圍壓σ′分別為30、50、70 kPa。由圖10可知,干砂初始相對密實度對殘余內摩擦角降比影響不大。

圖10 干砂土殘余應力狀態下不同初始相對密實度的影響

由靜三軸試驗可知,剪切初始階段,不同初始相對密實度的干砂試樣孔隙比差異較大,Dr=0.7時干砂試樣經歷強度上升階段、峰值應力階段、應變軟化階段,最終到達殘余應力狀態階段,即臨界狀態階段。Dr=0.4時干砂試樣,強度首先以較快的速率上升,隨后上升速率開始減慢,最終達到一個穩定的強度。此密實度下的干砂試樣強度一直在上升,最終的穩態強度與Dr=0.7的干砂試樣差異不大。臨界孔隙比與初始相對密實度大小無關,由于干砂在不同初始相對密實度下的最終孔隙比均接近臨界孔隙比,故不同初始相對密實度的干砂試樣殘余抗剪強度較為接近。因此,在給定的振動強度下,干砂殘余抗剪強度損失狀況差異不大,殘余內摩擦角降比差異也不大。

在60 Hz循環荷載作用下,飽和砂土初始相對密實度對殘余內摩擦角降比的影響結果見圖11。圖11中,砂土Dr分別為0.4、0.7,有效圍壓σ′分別為30、50、70 kPa。由圖11可知,Dr對飽和砂土殘余內摩擦角降比影響不大,即Dr對飽和砂土殘余抗剪強度損失影響不大。

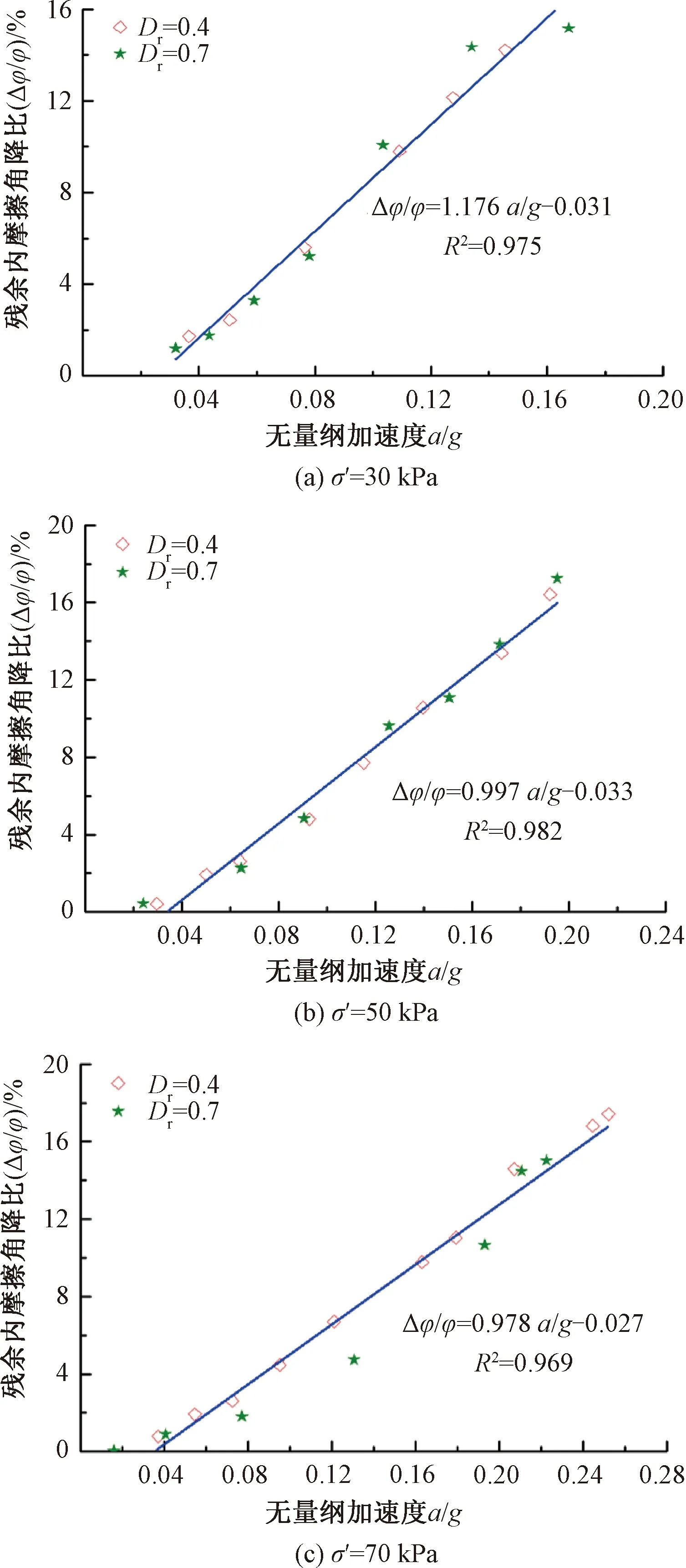
圖11 飽和砂土殘余應力狀態下不同初始相對密實度的影響

從上述試驗結果可以看出,初始相對密實度對砂土殘余內摩擦角降比的影響不大。針對此規律,干砂土與飽和砂土基本一致。

3.3 有效圍壓對砂土殘余內摩擦角的影響

(1)有效圍壓對干砂殘余內摩擦角降比的影響

有效圍壓對干砂內摩擦角降比的影響見圖12。對Dr分別為0.4、0.7的干砂試樣施加60 Hz循環荷載。當振動加速度a>0.02g時,隨著振動加速度的增大,干砂殘余內摩擦角降比隨加速度呈線性增大,此規律與有效圍壓大小無關,可以認為是無黏性材料自身的特性。

圖12 干砂殘余應力狀態下不同有效圍壓的影響

有效圍壓對干砂殘余內摩擦角降比的影響見圖12(a)。圖12(a)中,干砂試樣的Dr=0.4,有效圍壓σ′分別為30、50、70 kPa。由圖12(a)可知,當a≤0.02g時,干砂殘余內摩擦角降比較小,σ′對干砂殘余內摩擦角降比影響不顯著;當a>0.02g時,σ′的影響開始顯現。對于給定的振動加速度,隨著σ′增大,干砂殘余內摩擦角降比減小。當σ′從30 kPa增大到70 kPa時,Dr=0.7的干砂殘余內摩擦角降比相差最大可達16%。

圖12(b)同樣反映了Dr對干砂殘余內摩擦角降比的影響。圖12(b)中,選取Dr=0.7,σ′分別為30、50、70 kPa。由圖12(b)可知,當a≤0.02g時,干砂殘余內摩擦角降比較小,σ′對于殘余內摩擦角降比影響不顯著;而當a>0.02g時,σ′的影響開始顯現,對于給定的a,隨著σ′的增大,干砂殘余內摩擦角降比減小。當σ′從30 kPa增大到70 kPa時,Dr=0.7的干砂殘余內摩擦角降比相差最大可達13%。

(2)有效圍壓對飽和砂土殘余內摩擦角降比的影響

飽和砂土殘余內摩擦角降比同樣受到有效圍壓的影響較大。不同初始相對密實度下有效圍壓對飽和砂土殘余內摩擦角降比的影響見圖13。為便于對照,保證試驗結果的準確性,對Dr分別為0.4、0.7的飽和砂土試樣施加60 Hz循環荷載。在殘余應力狀態下,當a>0.02g,隨著a的增大,飽和砂土殘余內摩擦角降比都呈線性增大,此規律與施加的σ′大小無關,同樣可以認為這是無黏性材料自身的特性。

圖13 飽和砂土殘余應力狀態下不同有效圍壓的影響

由圖13(a)可知,對于Dr=0.4的飽和砂土試樣,當a≤0.02g時,飽和砂土殘余內摩擦角降比較小,幾乎可以忽略,此時σ′對飽和砂土殘余內摩擦角降比的影響不明顯。當a>0.02g時,σ′對飽和砂土殘余內摩擦角降比有顯著影響。即隨a的逐漸增大,σ′越大,飽和砂土殘余內摩擦角降比越小。原因與σ′對干砂殘余內摩擦角降比的影響相同。當σ′從30 kPa增大到70 kPa時,Dr=0.4的飽和砂土殘余內摩擦角降比相差最高可達6%。

由圖13(b)可知,σ′的影響規律與Dr=0.4的飽和砂土試樣基本一致,原因與相同密實度的飽和砂土相同。當σ′從30 kPa增大到70 kPa時,Dr=0.7的飽和砂土殘余內摩擦角降比相差最大可達7%。

綜上所述,σ′對干砂和飽和砂土的殘余抗剪強度損失有著重要影響,相對于飽和砂土,干砂受σ′的影響更大。

3.4 振動頻率對砂土殘余內摩擦角降比的影響

本試驗選取不同的振動頻率(1、5、10、15、20、25、30、35、40、60、80、100 Hz)研究振動頻率f對土體殘余抗剪強度損失的影響。音圈電機的輸出由安培力方程F=B×I×L控制,其產生的激振力與所施加的電流強度成正比。一個恒定的輸入功率對應于一個恒定的輸入力,因此采用控制輸入功率,改變f的方法來研究振動頻率對砂土殘余內摩擦角降比的影響。本節選取4個不同的輸入能量等級(level 1—level 4)來研究不同能量等級下振動頻率對砂土殘余內摩擦角降比的影響。

f對Dr=0.7、σ′3= 50 kPa的砂土殘余內摩擦角降比的影響見圖14。level 1—level 4是逐漸增大的輸入功率,其動應力逐級增大。對于固定的f,隨著輸入能量的增大,砂土殘余內摩擦角降比相應增大。輸入能量較低(level 1、level 2)時,f對砂土殘余內摩擦降比影響較小,高低頻振動產生的差異不顯著,即當音圈電機輸入功率較小時,試樣受到的振動幅值難以克服土體顆粒間摩擦,f對砂土抗剪強度損失的影響不大。

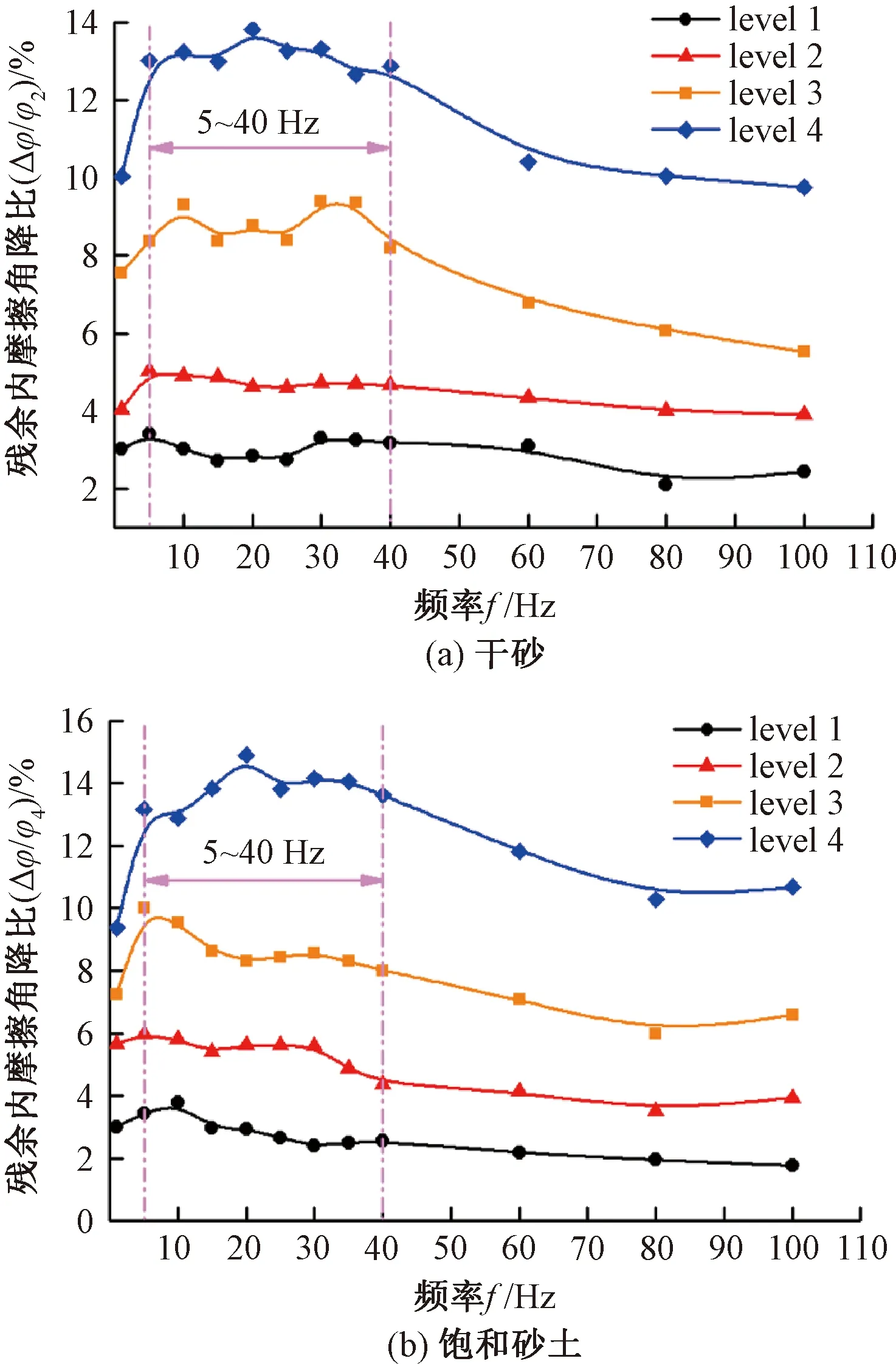
圖14 振動頻率對干砂、飽和砂土殘余內摩擦角降比的影響

當能量較高(level 3、level 4)時,振動頻率對砂土殘余內摩擦角降比影響較大,高低頻振動產生了明顯的差異。在f=1 Hz時,其殘余內摩擦角降比較小。在5～40 Hz頻率范圍出現砂土殘余內摩擦角降比最大的頻段。對于該敏感頻域范圍砂土摩擦角降比的突增,可能是該頻段范圍的振動引起試樣的共振。當f高于40～60 Hz時,砂土殘余內摩擦角降比隨f的增大而減小。當f>60 Hz時,砂土殘余內摩擦角降比差值較小,但仍然比低頻振動引起的內摩擦角降比大。

試驗結果表明,高頻振動產生的內摩擦角降低大于低頻循環荷載產生的影響,同時會產生一個引起砂土內摩擦角降比突增的敏感頻段[23]。對比振動頻率和加速度幅值兩個動力參數,可以發現振動加速度幅值對內摩擦角降比的影響占主導地位。對于敏感頻段的確定,將在后續研究中進行共振柱試驗,與砂土的共振頻率進行對比分析,從而建立殘余強度和振動頻率的定量關系。

4 結論

本文采用自主研制的可施加高頻循環荷載的三軸儀,在砂土接近殘余應力狀態下進行靜載與高頻循環荷載耦合的三軸試驗,研究砂土在不同初始狀態和振動條件下的殘余抗剪強度損失規律。通過對不同影響因素下砂土殘余抗剪強度損失規律的研究,主要得到如下結論:

(1)殘余應力狀態下,砂土在高頻循環荷載作用下會出現殘余抗剪強度損失的現象。當試樣接近殘余應力狀態時,所施加的高頻循環荷載會迅速引起試樣抗剪強度的損失。當振動停止后,隨著單調剪切的進行,試樣強度會恢復至之前的水平。即所施加的高頻循環荷載對砂土試樣振動前后的殘余抗剪強度沒有長期影響。

(2)振動加速度對砂土的殘余抗剪強度損失有較大影響。當振動加速度a≤0.02g時,砂土殘余內摩擦角降比與振動加速度關系不明顯。在此較小加速度范圍內,砂土殘余內摩擦角降比很小,幾乎可以忽略不計;當加速度a>0.02g時,隨著加速度幅值的增大,砂土殘余內摩擦角降比隨之增大,殘余內摩擦角降比與振動加速度幅值成正比。

(3)有效圍壓對高頻循環荷載作用下砂土的殘余抗剪強度損失有較大影響,該影響與加速度幅值有關。當加速度a≤0.02g時,有效圍壓對砂土殘余內摩擦角降比影響不大;而當加速度a>0.02g時,在給定的振動加速度條件下,有效圍壓越大,砂土殘余內摩擦角降比越小,有效圍壓與殘余內摩擦角降比成反比。砂土初始相對密實度和含水率對高頻循環荷載作用下砂土殘余抗剪強度損失的影響較小。

(4)振動頻率對砂土殘余內摩擦角降比有影響,引起砂土殘余內摩擦角降比最大的敏感頻段為5～40 Hz。當振動頻率高于40 Hz時,砂土殘余內摩擦角降比隨著振動頻率的增大而減小。振動加速度幅值對內摩擦角降比的影響大于振動頻率的影響。

為從機理上探究散體材料的高頻響應特征,本研究采用了粒徑較為統一的福建平潭標準砂,避免了散體材料參數變異性對實驗結果的影響。在后續研究中將進一步分析符合實際級配的基床散體填料在高頻荷載作用下的強度演化規律,揭示運行速度為400 km/h及以上高鐵路基基床可能存在的長期服役安全隱患,為其路基動力設計提供理論依據。